Galileu e o Plano inclinado As idéias de Aristóteles

Galileu e o Plano inclinado
As idéias de Aristóteles sobre o movimento dos corpos permaneceram
atuante por cerca de dois mil anos. Apenas no século XVII, Galileu deu um
grande passo na explicação do movimento dos corpos. Ele afirmou que "…
qualquer velocidade, uma vez estabelecida num corpo, se manterá constante,
desde que não existam causas de aceleração ou retardamento, fenômeno que
só será observado em planos aproximadamente horizontais onde a força de
atrito se tenha reduzido a um mínimo”. Surgindo assim o principio da inércia.
Galileu também estudou a queda dos corpos e verificou que ao contrario
do que os aristotélicos (seguidores das idéias de Aristóteles) pensavam corpos
com massas diferentes, lançados de uma mesma altura, caem em intervalos
de tempo iguais. Mas como Galileu chegou a conclusão que o movimento
uniforme não precisa de uma força para manter o corpo em movimento?
A maior dificuldade de Galileu era a medição dos intervalos de tempo e
do espaço percorrido pelo corpo em queda. Além de não possuir os
instrumentos adequados a medição do tempo (ele media o tempo utilizando
relógios d’água) o movimento de queda livre era muito rápido e os nossos
sentidos não consegue capta-lo com precisão. Para resolver esse problema
Galileu utilizou o plano inclinado. Plano inclinado é uma superfície plana e
inclinada que forma um ângulo menor que 90º com a superfície horizontal
assim como nossa animação do tobogã.
No livro "Diálogo a Respeito de duas Novas Ciências", Galileu apresenta
um diálogo, no qual o problema do plano inclinado é proposto e discutido,
entre Salviati, defensor de suas idéias; Sagredo, um aluno curioso e inteligente
e Simplício, que desenvolve as idéias aristotélicas.
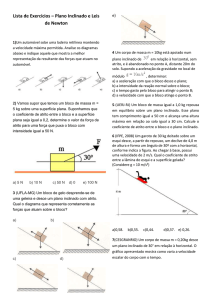
Estudando o movimento de diversos objetos sobre um plano inclinado ele
observou que quando um objeto rola de cima para baixo no plano inclinado o
objeto esta sujeito a uma aceleração, quando o objeto e lançado de baixo para
cima no plano inclinado, o objeto sofre uma desaceleração. Observe a figura
abaixo:
Figura 1
Figura 2
Figura 3
Veja que esta experiência levou Galileu a concluir que no caso dos planos
inclinados não serem ascendentes ou descendentes não deve haver aceleração
ou retardamento no movimento do corpo. "… O movimento ao longo de um
plano horizontal deve ser permanente." É obvio que Galileu sabia que
movimentos permanentes não existiam, mas se cada vez mais ele polisse o
plano inclinado, a esfera e o plano horizontal, o atrito entre os corpos
diminuiria e a esfera se movia durante um tempo maior com velocidade
constante.
Com
estes
argumentos
ele
convenceu-se
de
que
o
atrito
proporcionava as forças que diminuíam o movimento horizontal.
Aplicações do plano inclinado
Possivelmente o plano inclinado é a maquina simples mais antiga do
mundo. As civilizações primitivas já utilizavam superfícies inclinadas para subir
encostas e transportar cargas em desníveis. Acredita-se que a construção das
pirâmides do Egito foram facilitadas pelo plano inclinado. Mas, qual a
vantagem de se utilizar o plano inclinado?
Como já foi citado, Galileu tinha uma dificuldade de medir o tempo de
queda dos corpos devido o movimento ser demasiadamente rápido, no entanto
com o plano inclinado ele diminuía a atuação da aceleração da gravidade e
poderia analisar melhor o movimento.
Observe a figura:
Observe que o vetor que aponta na direção do movimento é uma
componente da força peso, observe também que esta componente diminui
com o ângulo, isto é enquanto menor a inclinação, menor será a componente
do peso na direção do movimento, portanto uma menor aceleração.
Podemos também concluir que para elevar um mesmo objeto a uma mesma
altura utilizando um plano inclinado, na medida do possível, devemos escolher
aquele que possui a menor inclinação.
O parafuso também é uma aplicação do plano inclinado, que
nada mais é do que um plano inclinado enrolada em um cilindro.
Assim, com o auxilio desse instrumento, Galileu Galilei pôde
estudar o movimento uniformemente variado.