Lista 14 - Oscilacoes

Lista 14: Oscilações
Lista 14: Oscilações
NOME:______________________________________________________________________
Matrícula:
Turma
Turma:
Prof. :
Importante:
i.
ii.
iii.
iv.
Nas cinco páginas seguintes contém problemas para se resolver e entregar.
Ler os enunciados com atenção.
Responder
esponder a questão de forma organizada, mostrando o seu raciocínio de forma coerente.
Analisar a resposta respondendo: ela faz sentido? Isso lhe ajudará a encontrar erros!
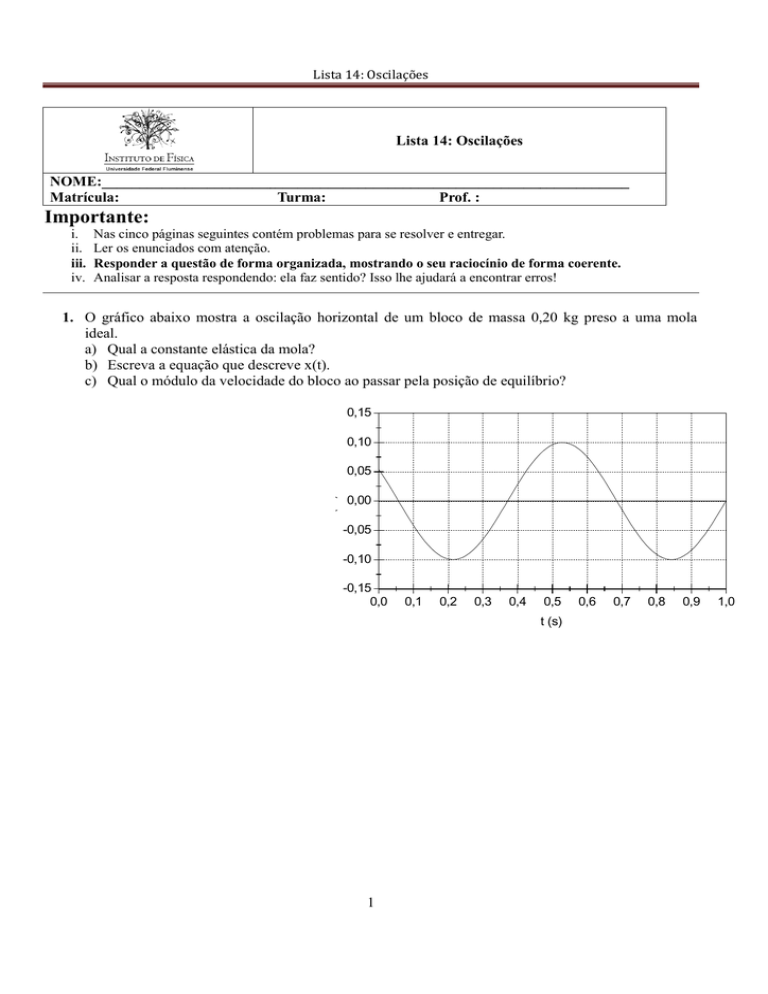
1. O gráfico abaixo mostra a oscilação horizontal de um bloco de massa 0,20 kg preso a uma mola
ideal.
a) Qual a constante elástica da mola?
b) Escreva a equação que descreve x(t).
c) Qual o módulo da velocidade do bloco ao passar pela posição de equilíbrio?
0,15
0,10
x (m)
0,05
0,00
-0,05
-0,10
-0,15
0,0
0,1
0,2
0,3
0,4
0,5
t (s)
1
0,6
0,7
0,8
0,9
1,0
Lista 14: Oscilações
2. Um bloco de 1,0 kg está sobre uma superfície horizontal sem atrito e preso a uma mola ideal
horizontal. Aplica-se uma força horizontal F = 20,0 N ao bloco para mantê-lo em repouso a 0,20 m
de sua posição de equilíbrio (x = 0). Cessada a aplicação da força F o bloco executa um MHS.
Determine:
a) O período e a freqüência do movimento,
b) A aceleração máxima do bloco,
c) A velocidade do bloco ao passar pela posição x = - 0,10 m,
d) A energia cinética do bloco em função de sua posição x.
2
Lista 14: Oscilações
3. Um bloco de 175 g preso a uma mola ideal de constante elástica 155 N/m executa um MHS sobre um
trilho de ar horizontal. Em dado instante o corpo passa a 3,00 cm da posição de equilíbrio com
velocidade de 0,815 m/s. Determine a amplitude, o período e a velocidade máxima do corpo.
3
Lista 14: Oscilações
4. Uma mola ideal com constante elástica de 15,0 N/m está pendurada no teto. Um corpo de massa 500
g é preso à extremidade livre da mola baixado lentamente até a posição de equilíbrio. Depois, ele é
puxado 6,0 cm para baixo e abandonado. Qual a constante de tempo se após 30 oscilações a
amplitude é igual a 3,0 cm?
4
Lista 14: Oscilações
5. Um cilindro sólido de massa M = 4,0 kg está sobre uma superfície horizontal, preso pelo seu eixo a
uma mola ideal horizontal de constante elástica k = 2,70 N/cm. O cilindro é afastado de 20,0 cm de
sua posição de equilíbrio e abandonado a partir do repouso. O cilindro rola sem deslizar.
a) Mostre que o CM do cilindro executa um MHS com período de = 23M⁄2 .
b) Calcule as energias cinéticas de translação e de rotação do cilindro quando este passar pela
posição de equilíbrio,
5
Lista 14: Oscilações
Questões:
(A) Em um oscilador harmônico simples como é afetada, pela duplicação da amplitude, cada uma das
seguintes grandezas: período, energia mecânica total, velocidade máxima e aceleração máxima?
(B) O diapasão é um dispositivo utilizado pelos músicos na afinação de instrumentos musicais. O diapasão
executa MHS?
(C) Em que ponto do movimento de um pêndulo simples a tração no fio atinge o valor máximo? E o valor
mínimo?
(D) Uma pessoa está em pé sobre uma balança de banheiro que está sobre uma plataforma suspensa por
uma grande mola. A plataforma executa um movimento harmônico simples vertical. Descreva a
variação de leitura da escala da balança durante um período.
(E) No projeto de uma estrutura numa região propensa a terremotos, qual deve ser a relação entre a
frequência da estrutura e a frequência típica de terremoto? A estrutura deve possuir amortecimento
grande ou pequeno?
Exercícios e Problemas
1. Um bloco de massa M preso a uma mola de constante k descreve um movimento harmônico simples
horizontal com amplitude A1. No instante em que o bloco passa pela posição de equilíbrio, um pedaço
de massa de vidraceiro, de massa m, cai verticalmente de uma pequena altura sobre o bloco e gruda
nele. a)calcule a nova amplitude e o período. b) repita o item (a) supondo que a massa caia sobre o
bloco no instante em que ele está na extremidade de sua trajetória.
2. Um corpo de 0,500 kg oscila preso a uma mola ideal. A velocidade do corpo é dada pela função
V(t) = 3,60 sen (4,71.t – 1,57), para t em s e V em cm/s. Determine: a) o período; b) a amplitude; c) a
aceleração máxima; d) a constante elástica da mola.
3. Um bloco de 0,400 kg está em repouso, pendurado em uma mola ideal de constante elástica 78,4 N/m.
O bloco é levantado desta posição até uma posição situada 15,0 cm acima e abandonado a partir do
repouso.
a) Qual a amplitude de oscilação?
b) Qual a força elástica e a força resultante em cada ponto extremo da trajetória do bloco?
c) Qual o período de oscilação?
d) Qual a velocidade máxima do bloco?
4. Um oscilador consiste em um bloco preso a uma mola de constante elástica 456 N/m. Num dado
instante o bloco passa pela posição 0,112 m, medida em relação a sua posição de equilíbrio, com
velocidade de -13,6 m/s e aceleração de -123 m/s2. Calcule a massa do bloco, a freqüência e a
amplitude de oscilação.
5. Este processo tem sido realmente usado para “pesar” astronautas no espaço. Uma cadeira de 42,5 kg é
presa a uma mola e deixada oscilar livremente. Quando vazia, a cadeira leva 1,30 s para completar uma
oscilação. Mas, com uma astronauta sentada nela, sem apoiar os pés,no chão, a cadeira leva 2,00 s para
completar um ciclo.Qual é a massa da astronauta?
6
Lista 14: Oscilações
6. Exercício corrigido em aula de monitoria
Um bloco de 0,20 kg está preso a uma mola ideal de constante elástica de 28,8 N/m executando um
MHS horizontal. Em t = 0 o bloco passa pela sua posição de equilíbrio (x = 0) com velocidade de 1,2
m/s no sentido oposto do eixo x. Escreva a equação da posição em função do tempo.
7. Um bloco m está sobre outro bloco M executando um MHS sobre uma superfície horizontal sem atrito
com freqüência de 1,50 Hz, como mostra a Fig. 1. O coeficiente de atrito estático entre os dois blocos é
0,600. Qual a amplitude máxima de oscilação do sistema para m não deslizar sobre M?
8. Exercício corrigido em aula de monitoria
Um bloco de massa m está sobre uma superfície horizontal e preso a uma mola ideal de constante
elástica k. Outro bloco de massa M é encostado no bloco m, como mostra a figura, empurrando-os de
modo a comprimir a mola de X. Nesta posição, o sistema é abandonado do repouso e desliza sobre a
superfície sem atrito. Dados: X = 10,0 cm e M = 3m
a) A partir de qual posição um bloco perderá o contato com o outro?
m M
b) Qual a distância entre os blocos quando o bloco m atingir o repouso
pela 2a vez após a perda de contato com M?
9. Um pêndulo é constituído por uma partícula de massa M pendurada na extremidade de uma barra fina
de massa desprezível e comprimento L. Uma mola de constante elástica k é conectada a barra a uma
distância h abaixo do ponto de suspensão, Fig.2. Encontre a frequência angular do sistema para valores
pequenos da amplitude θ.
10. Uma barra delgada e homogênea de massa M (Fig. 3) possui um pivô em uma das extremidades e na
outra, uma mola vertical de constante elástica k. Mostre que a barra quando deslocada de um pequeno
ângulo θ de sua posição de equilíbrio horizontal e liberada, realiza um movimento harmônico simples
de freqüência angular = 3 ⁄M.
m
M
Fig. 1
Fig. 2
Fig. 3
Respostas:
1)a) ⁄ ; 2 ⁄ ; b) ; 2 ⁄
2)a) 1,33 s; b) 0,764m; c)16,9 m/s2; d) 11,1N/m
3)a) 15,0 cm; b)posição superior: Fel =7,84 N e R=11,8 N; posição inferior: Fel = 15,7 N e R = 11,8 N; c)
0,449 s; d)2,10 m/s
4) 0,416 kg; 5,27 Hz; 0,426 m
5) 58,1 kg
6) 0,10 cos12. 1,6, t em s e x em m
7) 0,066 m
8) a) posição de equilíbrio; b)28,6 cm
9) ! ⁄ 7