(0,5 ) 3,0 P i VA Watts ε

Aula exploratória 07.
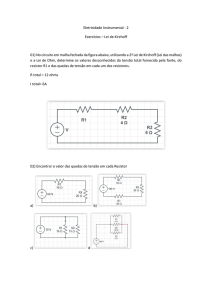
Questão 01: Um resistor de 11Ω é ligado aos terminais de uma bateria com fem de 6V
e resistência interna de 1Ω. Determine:
(a) a corrente;
(b) a tensão útil da bateria (isto é, Va − Vb );
(c) a potência fornecida pela fonte da fem ;
(d) a potência fornecida ao resistor externo;
(e) a potência dissipada pela resistência interna da bateria. Em que condição a potência
dissipada no resistor externo é máxima?
(f) se a bateria for de 150 A.h., qual será a energia nela armazenada?
a
r
R
ε
b
a) Aplicando a lei das malhas ao circuito, temos:
ε − r i − R i = 0 ⇒ (r + R ) i = ε
⇒ i=
ε
(r + R )
.
(1)
b) A tensão útil na bateria é:
Va − Vb = ε − i r = 6 V − (0,5 A) (1,0 Ω ) = 5,5 V .
(2)
c) A potência fornecida pela fonte é:
P = ε i = (6,0V ) (0,5 A) = 3,0Watts .
(3)
d) A potência fornecida ao resistor externo é:
P = R i 2 = (11Ω) (0,5 A) 2 = 2,75Watts .
(4)
Para obter a máxima potência dissipada temos de (4) e (1) que
R
dP
1
2R
;→
= 0 ⇒ ε 2(
−
)=0
2
2
(r + R)
dR
( r + R ) ( r + R )3
ou r − R = 0 ⇒ R = r.
Uma bateria real sempre tem uma resistência interna r.
P =ε2
1
PED – Todas as turmas.
Aula exploratória 07.
e) A potência dissipada pela resistência interna da bateria é:
P = r i 2 = (1Ω) (0,5 A) 2 = 0, 25Watts .
(5)
e) Se a bateria for de 150 A.h., qual será a energia nela armazenada?
Pfem =
dU
= ε i ⇒ dU = ε i dt
dt
(6)
J 
C

∴ U = (6,0 V ) (150 A) (3600 s ) =  6,0  150  (3600 s ) = 3,24 MJ
C
s

2
PED – Todas as turmas.
Aula exploratória 07.
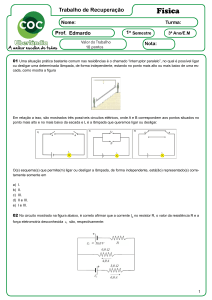
Questão - 02. Qual a corrente em termos de ε e R, indicada pelo amperímetro A da
figura? Suponha que seja nula a resistência do amperímetro.
R
2R
A
ε
R
R
R. Aplicando a regra das malhas ao circuito, devemos ter:
i1 + i 2
i2
i1
i1
ε
1
i3
i3
A
3
i 2 − i3
i1 + i 3
2
i1 + i 3
i1 + i 2
i2
i 2 − i3
Da malha 1, encontramos:
i 2 R − i 1 (2 R ) = 0 ⇒ i 2 = 2 i 1
(1)
Da malha 2:
(i 2 − i 3 )R − (i1 + i 3 )R = 0
⇒ i 2 − i1 = 2 i 3
(2)
Substituindo ( 1 ) em ( 2 ):
Da malha 3:
2i 1 − i1 = 2 i 3 ⇒ i 1 = 2 i 3
(3)
(
(4)
)
ε − i 1 (2 R ) − i 1 + i 3 R = 0
Substituindo ( 3 ) em ( 4 ) e isolando i 3 :
ε − 4 Ri 3 − 3Ri 3 = 0 ⇒ i 3 =
ε
7R
(5)
3
PED – Todas as turmas.
Aula exploratória 07.
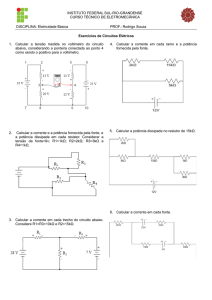
Questão 03: Uma bateria de 6V, com resistência interna desprezível, é utilizada para
carregar um capacitor de 2µF através de um resistor de 100Ω. Determine:
a) A corrente inicial;
b) A carga final no capacitor;
c) O tempo necessário para a carga atingir 90,0% do seu valor final;
d) a carga quando o valor da corrente for igual à metade do seu valor inicial.
O circuito do enunciado é mostrado na figura abaixo:
S
R
ε
C
a) Considerando que inicialmente o capacitor encontra-se descarregado, ao
conectarmos a chave S, a corrente inicial será:
i=
ε
R
=
6V
= 0,06 A .
100 Ω
(1)
b) A carga final no capacitor será:
qmax = ε C = (6 V ) (2 µ F ) = 12 µ C .
(2)
c) Ao fecharmos o circuito, pela lei das malhas, teremos:
ε −iR −
Mas, i =
q
=0.
C
(3)
dq
. Que substituindo em ( 3 ) resulta:
dt
R
dq q
+ =ε
dt C
⇒ RC
Como ε C = c te ⇒
RC
dq
+ q = εC
dt
d
(ε C ) = 0. Logo,
dt
(4)
d
 q ( t ) − ε C  +  q ( t ) − ε C  = 0
dt 
4
PED – Todas as turmas.
Aula exploratória 07.
Fazendo
u (t ) = q (t ) − ε C na equação (4) acima:
RC
∫
du
=−u ⇒
dt
du
1
=−
dt
u
RC
du
1
=−
dt
u
RC ∫
(5)
u 
t
ln   = −
⇒ u ( t ) = u0 e
u
R
C
 0
u0 = u (t = 0) = q (0) − ε C = −ε C
t
−
RC
Dessa forma, em função de q , temos:
q ( t ) − ε C = −ε C e
−
t
RC
t
−


RC
⇒ q ( t ) = ε C 1 − e





Quando a carga atinge 90% do valor máximo, teremos que
(6)
q (t ) = 0,9 5ε C . Logo:
t
t
−
−


RC
RC
0,90 ε C = ε C 1 − e
= 1 − 0,90
 ⇒ e




(7)
t
−
= ln ( 0,10 ) ⇒ t = − R C ln ( 0,10 )
RC
t = − (100Ω )( 2 µ F )( -2,3) = 3,3τ C = 460 µs = 046ms
d) Quando a corrente for igual à metade do valor inicial, i (t ) =
1ε
e a equação (3)
2R
deve ser:
ε−
ε R
R2
−
q (t )
= 0.
C
(8)
Isolando a carga na equação (8), temos:
5
PED – Todas as turmas.
Aula exploratória 07.
ε 
1
1

q (t ) =  ε −  C = ε C = q (t = ∞)
2
2
2

q (t ) = 0,5 × 6V × 2 µ F = 6 µC
(9)
ou
0, 06 A


q (t ) =  6 V −
100Ω  2 µ F
2


∴ q (t ) = 6 µ C
6
PED – Todas as turmas.
Aula exploratória 07.
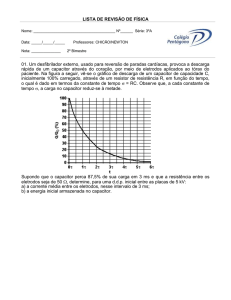
Questão 04: No circuito que aparece abaixo o capacitor está inicialmente descarregado
com a chave aberta. Após ligar a chave S, em t = 0 s, calcule:
(a) a corrente que passa pela chave S, imediatamente após a ligação;
(b) a corrente que passa pelo resistor R1 em função do tempo;
(c) a carga do capacitor C em função do tempo;
(d) a corrente através de R2 em função do tempo;
(e) a corrente que passa pela chave S em função do tempo;
(f) após abrir a chave S, quanto tempo leva para a carga do capacitor chegar a 36,8%
(=1/e) do valor que possuía quando a chave foi aberta?
C
R2
R1
S
a) Como o capacitor encontra-se inicialmente descarregado, logo que a chave é fechada,
ele se comporta como um fio condutor, deixando a corrente passar livremente:
ε
R1
R2
⇒
ε
R12
S
S
Dessa forma, a resistência equivalente será:
R1 + R 2
1
1
1
=
+
=
R12 R1 R 2
R1 R 2
⇒ R12 =
R1 R 2
R1 + R 2
.
(1)
Aplicando a lei das malhas ao circuito composto pela fonte e a resistência R12 :
ε − i R12 = 0 ⇒ i =
ε
R12
=
(
ε R1 + R 2
R1 R 2
)
.
(2)
b) e c) a corrente que passa pelo resistor R1 em função do tempo
7
PED – Todas as turmas.
Aula exploratória 07.
ε
1
S
C
ε
2
R1
R2
S
A lei das malhas aplicada à malha 1, resulta em:

−

q
ε − − i1 R1 = 0 ⇒ q (t ) = ε C 1 − e
C


t
R1 C


.


(3)
b) Derivando a equação ( 4 ) em função do tempo, temos:
 ε  −
i 1 (t ) =   e
 R1 
 
t
R1 C
(4)
.
c) a carga em C em função do tempo
t
−


q
R1 C

ε − − i1 R1 = 0 ⇒ q(t ) = ε C 1 − e


C


(5)
d) A lei das malhas aplicada à malha 2, resulta em:
ε − i2 R2 = 0 ⇒ i2 =
ε
R2
.
(6)
e) Dessa forma, a corrente que passa pela fem em um tempo t em que a chave está
fechada será:
 ε  −
i (t ) = i 1(t ) + i 2 =   e
 R1 
 
t
R1 C

−
 1
1
+
=ε
+
e
R2
 R 2 R1

ε
t
R1 C


.


(7)
8
PED – Todas as turmas.
Aula exploratória 07.
f) Após o capacitor ser carregado, abrindo a chave S, o circuito se resume a:
C
R1
R2
Aplicando a lei das malhas ao circuito:
−
q
dq
q
− i R1 − i R 2 = 0 ⇒ ( R1 + R 2 )
=−
C
dt
C
dq
dt
=−
q
C ( R1 + R 2 )
⇒ q (t ) = qmax e
−
(8)
t
C (R1 + R 2 )
Quando a carga atinge 36,8% do valor inicial, teremos:
0,368qmax = qmax e
−
t
C ( R1 + R 2 )
⇒ ln (0,368) = −
t
C ( R1 + R 2 )
( 9)
t = − ln (0,368) C ( R1 + R 2 ) = −(−1, 0) (1 µ F ) (10 k Ω) = 10 ms
9
PED – Todas as turmas.
Aula exploratória 07.
Questão 05. Um capacitor, inicialmente descarregado, foi totalmente carregado por um
dispositivo de fem constante ligado em série com um resistor R.
a) Mostre que a energia final armazenada no capacitor é metade da energia fornecida
pela bateria;
b) Por integração direta de R i 2 no tempo de carregamento, mostre que a energia
térmica dissipada pelo resistor é também metade da energia fornecida pela fem ;
c) há uma maneira alternativa de resolver o item b)?
a) - A potência desenvolvida pela bateria é:
∞
P (t ) = ε i (t ) , logo U ( fornecida) = ∫ P(t )dt , mas de
0
ε − Ri −
ε − t / RC
q
e
= 0 , temos i ( t ) =
. Portanto,
R
C
∞
U ( fornecida) = ε ∫
0
ε
R
e −t / RC dt = Cε 2 .
1
1
Por outro lado temos que U C = C V 2 = C ε 2 . Ou seja
2
2
1
U C = U ( fornecida ).
2
b) – A energia dissipada:
∞
∞
1
ε − t / RC 2
ε 2 −2t / RC
Cε 2
U (dissipada em R ) = R ∫ ( e
) dt =
e
dt =
.
2 0 R
2 R ∫0
2
Logo
1
U R = U ( fornecida ).
2
c) – Conservação de energia:
Cε 2
U ( fornecida ) − U C (armazenada ) = U R (dissipada ) =
.
2
10
PED – Todas as turmas.
Aula exploratória 07.
Questão 6. (Tempo sobrando): Quando são acesas as luzes de um automóvel, um
amperímetro em série com elas marca 10 A e a leitura de um voltímetro ligado entre as
suas extremidades marca 12 V (ver figura abaixo). Quando o motor de partida elétrico é
ligado, a leitura do amperímetro cai para 8,0 A e as luzes ficam um pouco mais fracas.
Se a resistência interna da bateria for de 0,05 Ω e a do amperímetro for desprezível,
determinar: a) A fem da bateria e b) a corrente que atravessa o motor de partida
quando as luzes estão acesas.
Solução:
11
PED – Todas as turmas.