Lista de Exercícios - 1º Bimestre – Sistemas III – Dilatação

Lista de Exercícios - 1º Bimestre – Sistemas III – Dilatação, Calorimetria e Gases Ideais
Prof. Dr. Cláudio S. Sartori
Dilatação Térmica e Calorimetria
1. O pêndulo de um relógio é feito de alumínio.
Qual a variação fracional do seu comprimento, quando
ele é resfriado, passando de 25°C para 10°C?
2. Uma trena de aço de 25 m está correia à
temperatura de 20°C. A distância entre dois pontos,
medida com a trena num dia em que a temperatura é
de 35°C, é de 21,64 m. Qual a distância real entre os
dois pontos?
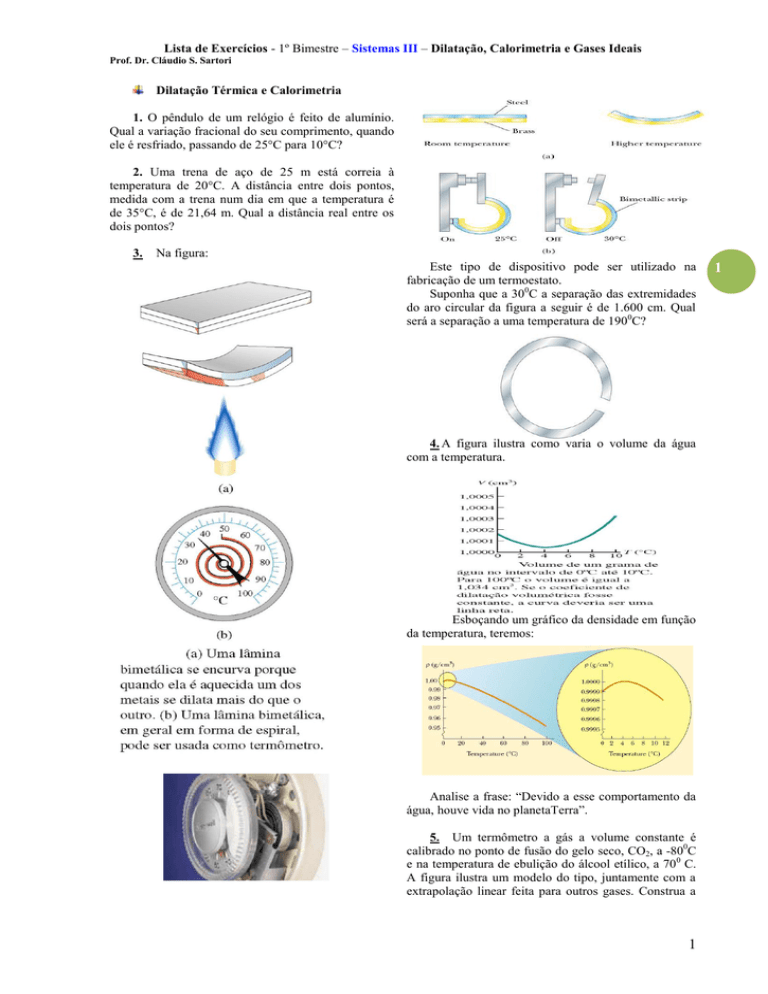
3.
Na figura:
Este tipo de dispositivo pode ser utilizado na
fabricação de um termoestato.
Suponha que a 300C a separação das extremidades
do aro circular da figura a seguir é de 1.600 cm. Qual
será a separação a uma temperatura de 1900C?
4. A figura ilustra como varia o volume da água
com a temperatura.
Esboçando um gráfico da densidade em função
da temperatura, teremos:
Analise a frase: “Devido a esse comportamento da
água, houve vida no planetaTerra”.
5. Um termômetro a gás a volume constante é
calibrado no ponto de fusão do gelo seco, CO2, a -800C
e na temperatura de ebulição do álcool etílico, a 70 0 C.
A figura ilustra um modelo do tipo, juntamente com a
extrapolação linear feita para outros gases. Construa a
1
1
Lista de Exercícios - 1º Bimestre – Sistemas III – Dilatação, Calorimetria e Gases Ideais
Prof. Dr. Cláudio S. Sartori
relação P versus T do termômetro mencionado,
10. Colocam-se 600 g de granalha de Pb a uma
sabendo que as pressões correspondentes são, temperatura inicial de 100 0C, num calorímetro de
respectivamente, 0.900 atm e 1.635 atm .
alumínio, com a massa de 200 g, contendo 500 g de
H2O, inicialmente a 17.3 0C. A temperatura final de
equilíbrio do calorímetro com a granalha é de 20.0 0C.
Qual o calor específico do chumbo?
Dado: cAl = 0.9 kJ/(kg.K).
11. Qual a quantidade de calor necessária para
aquecer 2kg de gelo, à pressão de 1 atm, de -25 0C, até
que toda a amostra tenha se transformado em vapor de
água?
Dados:
Calor específico latente de fusão da água:
Lf = 333.5 kJ/kg
Calor específico latente de vaporização da
água:
Lv = 2257 kJ/kg
Calor específico do gelo:
cg = 2.05 kJ/(kg.K).
12. Um jarro de limonada está sobre uma mesa de
piquenique a 33 0C. Uma amostra de 0.24 kg desta
limonada é derramada num vaso de espuma de plástico
e a ela se juntam 2 cubos de gelo. (cada qual com
0.,025 kg a 00C). (a) Admita que não haja perda de
calor para o ambiente. Qual a temperatura final da
limonada ? (b) Qual seria a temperatura final se fossem
6 cubos de gelo ? Admita que a capacidade calorífica
da limonada seja a mesma da água.
13. O pêndulo de um relógio é feito de alumínio.
Qual a variação fracional do seu comprimento, quando
ele é resfriado, passando de 25°C para 10°C?
6. Um estudante ingeriu em um jantar cerca de
200 Cal (1 Cal =1 000cal e 1 cal = 4.18 J). Ele deseja
“queimar” essa energia adquirida, fazendo o
levantamento de peso de 50 kg em uma academia.
Quantas vezes ele deve levantar esse peso? Assuma
que a cada “puxada” no aparelho, o peso levanta-se
cerca de 2.0 m.
7. Uma placa de metal de 0.05kg é aquecida a
2000C e em seguida colocada em um recipiente com
0.400 kg de água a 200C. A temperatura de equilíbrio
térmico é de e = 22.40C. Determine o calor específico
do metal. Dado: cágua = 4186 J/(kg.K)
14. Uma trena de aço de 25 m está correia à
temperatura de 20°C. A distância entre dois pontos,
medida com a trena num dia em que a temperatura é de
35°C, é de 21,64 m. Qual a distância real entre os dois
pontos?
15. Uma quantidade 300g de gelo a -35°C é
colocado em um calorímetro de alumínio. Há uma peça
de ferro de 50g a temperatura ambiente de 22 0C no
interior do calorímetro. Adiciona-se 1500 g de água a
800C. Calcule:
(a) o calor total necessário para derreter
completamente o gelo.
(b) A temperatura de equilíbrio do sistema.
DADOS:
cFe = 0,47 g JC
8. Um cowboy atira com uma arma sobre uma
moeda colocada em uma parede. A bala sai da arma a
200 m/s. Se toda a energia do impacto for convertida
5 J
na forma de calor, qual será o aumento de temperatura Calor latente de fusão do gelo: 3, 5 10 kg
da bala? Dado: calor específico do material que
Calor específico do gelo: 2301 kgJ C .
constitui a bala: cb = 234 J/(kg.K).
Calor específico da água: 4186 kgJ C .
9. Determine a quantidade de calor para se
16 – Coloca-se uma amostra de 220 g de
elevar de 25 0C a temperatura de 5 kg de cobre.
ferro, a temperatura de 100°C, num calorímetro
Dado: cCu = 0.386 kJ/(kg.K)
contendo 300 g de água, inicialmente a 20°C. O
calorímetro é de alumínio e sua massa de 200 g. Sua
2
2
Lista de Exercícios - 1º Bimestre – Sistemas III – Dilatação, Calorimetria e Gases Ideais
Prof. Dr. Cláudio S. Sartori
temperatura final é de 25°C. Calcular o calor
específico da amostra.
Dados: cH2O =4,19 g JC ; cAl = 0,91 g JC
10 – Coloca-se uma amostra de 120 g de
ferro, a temperatura de 150°C, num calorímetro
contendo 300 g de água, inicialmente a 20°C. O
calorímetro é de alumínio e sua massa de 200 g. Sua
temperatura final é de 25°C. Calcular o calor
específico da amostra.
Dados:
cH2O =4,19 g JC ; cAl = 0,91 g JC
cFe = 0,47
J
g C
3
11 - Uma quantidade 300g de gelo a -25°C é
colocado em uma caixa de isopor. Qual o calor
necessário para transformar toda essa quantidade de
gelo em vapor de água a 1000C ?
DADOS:
Calor latente de fusão do gelo: 3, 5 105 kgJ
Calor específico do gelo: 2301 kgJ C .
Calor específico da água: 4186
J
kg C
.
12 – A haste de um relógio de pêndulo é feita
de latão. Calcule a variação do comprimento quando
ela é resfriada de 19.5 0C até 5 0C?
13 – Observando a curva do calor específico
da água em relação a temperatura, calcule a variação
de calor sensível para uma massa de 200 g de água,
quando aquecida de 0 a 40 0C.
3
Lista de Exercícios - 1º Bimestre – Sistemas III – Dilatação, Calorimetria e Gases Ideais
Prof. Dr. Cláudio S. Sartori
Propagação de Calor
1. Condução através de uma geladeira de
isopor. Uma caixa de isopor usada para manter
bebidas frias em um piquenique possui área total
(incluindo a tampa) igual a 0.80m2 e a espessura da
parede é de 2.0 cm. Ela está cheia de água, gelo e latas
de Omni-Cola a 00C. Qual é a taxa de fluxo de calor
para o interior da caixa se a temperatura da parede
externa for igual a 300C? Qual a quantidade de gelo
que se liquefaz durante um dia?
Dado:
isopor=0.010 W/(m.K)
4. Radiação do corpo humano. Sabe-se que a área
total do corpo humano é igual a 1.20m2 e que a
temperatura da superfície é 300C = 303K. Calcule a
taxa total de transferência de calor do corpo por
radiação. Se o meio ambiente está a uma temperatura
de 200C, qual é a taxa resultante do calor perdido pelo
corpo por radiação? A emissividade e do corpo é
próxima da unidade, independentemente da cor da pele.
Dados: Lei de Stefan-Boltzmann:
H A e
H A e
T4
T 4 Ts4
4
Constante de Stefan-Boltzmann:
5.67 10 8
W
m K4
2
5. Uma placa quadrada de aço, com lado igual a 10
cm, é aquecida em uma forja de ferreiro até uma
temperatura de 8000C. Sabendo que a emissividade é
igual a 0.60, qual é a taxa total de energia transmitida
2. Uma barra de aço de 10.0 cm de comprimento é por radiação?
soldada pela extremidade com uma barra de cobre de
6. Um chip com embalagem de cerâmica de 40 pinos
20.0 cm de comprimento. As duas barras são
possui
rtérm = 40 K/W. Se a temperatura máxima que o
perfeitamente isoladas em suas partes laterais. A seção
circuito
pode tolerar com segurança não pode superar
reta das duas barras é um quadrado de lado 2.0 cm. A
0
0
120
C,
qual
é o mais elevado nível de potência que o
extremidade livre da barra de aço é mantida a 100 C
circuito
pode
tolerar com segurança para uma
colocando-a em contato com vapor d’água obtido por
temperatura
ambiente
igual a 750C?
ebulição, e a extremidade livre da barra de cobre é
mantida a 00C colocando-a em contato com o gelo.
Calcule a temperatura na junção entre as duas barras e
a taxa total da transferência de calor.
dQ
dt
A T
e
R
e
A
3. No exemplo anterior, suponha que as barras
estejam separadas. Uma extremidade é mantida a
1000C e a outra extremidade é mantida a 00C. Qual a
taxa total de transferência de calor nessas duas barras?
7. Tira-se de uma fornalha uma peça fundida pesando
50 kgf, quando a temperatura era de 400°C, sendo
colocada num tanque contendo 400 kg de óleo a 30°C.
A temperatura final é de 40°C e o calor específico do
óleo, 0,5 cal-g-1 (0C)-1. Qual o calor específico da peça
fundida? Desprezar a capacidade calorífica do tanque e
quaisquer perdas de calor.
Qo Qp
0
mo co
400 0,5 40 30
cp
o
mp c p
50 cp 40 400
0
p
0
0,11 gcal0C
8. A evaporação do suor é um mecanismo importante
no controle da temperatura em animais de sangue
quente. Que massa de água deverá evaporar-se da
superfície de um corpo humano de 80 kg para resfriá-lo
1°C? O calor específico do corpo humano é
aproximadamente l cal g -1 • (°C) -1 e o calor latente de
vaporização da água na temperatura do corpo (37°C) é
de 577 cal • g -1.
4
Lista de Exercícios - 1º Bimestre – Sistemas III – Dilatação, Calorimetria e Gases Ideais
Prof. Dr. Cláudio S. Sartori
Quantidade de calor perdida pelo corpo
humano na variação de 10C:
Q
QL
mc
1
1,986 10 25
E eV
nm 1,6 10 19 10 9
1240
E eV
nm
Q 80000 1 1 80000cal
mLv
QL
Lv
m
80000
138.65g
577
9. Para as radiações abaixo, dados os
intervalos extremos de comprimento de onda, encontre
os intervalos correspondentes em freqüência (Hz) e
energia (eV).
Espect
ro
visível
Visibl
e
Core
s
f
min
fEmaxmin
f
max
min
14
(nm)
(10 Hz)
(eV)
c
f
E
E eV
622 -770
3,896 –
4,823
1,61 – 1,99
Orang
e–
Laranj
a
597 - 622
4,823 –
5,025
1,99 – 2,08
Yello
w–
Amare
lo
577 - 597
Green
–
Verde
492 - 577
Blue –
Azul
455 - 492
Violet
–
Violet
a
390 - 455
f
3 108
622 10
f
f
3 108
770 10
9
f
f max
f min
E
h f
E h
11. Raios de estrelas. A superfície quente e
brilhante de uma estrela emite energia sob a forma de
radiação eletromagnética. É uma boa aproximação
considerar e = 1 para estas superfícies. Calcule os raios
das seguintes estrelas (supondo que elas sejam
esféricas):
(a) Rigel, a estrela brilhante azul da
constelação Órion, que irradia energia com uma taxa de
2.7.1032W e a temperatura na superfície é igual a
11000K.
(b) Procyon B (somente visível usando um
telescópio), que irradia energia com uma taxa de
2.1.1023W e a temperatura na sua superfície é igual a
10000K.
(c) Compare suas respostas com o raio da
Terra, o raio do Sol e com a distância entre a Terra e o
Sol. (Rigel é um exemplo de uma estrela supergigante e
Procyon B é uma estrela anã branca.
4,823 1014
34
J s
Dados: condutividade térmica:
cobre: Cu 385,0 J(s m°C)-1
c
aço:
6,62 10
1,61
12. Determine o comprimento da barra
indicado para que o fluxo de calor seja de 250W.
8
E
Emin eV
3,8961 1014
9
h 6,62 10
c
1240
770
10. Área do filamento de uma lâmpada de
tungstênio. A temperatura de operação do filamento de
Emaxtungstênio de uma lâmpada incandescente é igual a
2450K e sua emissividade é igual a 0.35. Calcule a área
da superfície do filamento de uma lâmpada de 150 W
supondo que toda a energia elétrica consumida pela
1240
lâmpada seja convertida em ondas eletromagnéticas
nm
pelo filamento. (Somente uma fração do espectro
irradiado corresponde à luz visível.)
Red –
Verme
lho
c
Emin eV
34
Aço
50,2 J(s m°C)-1
3 10
1,986 10 25
m
1eV=1,6 10-19J
E J
5
5
Lista de Exercícios - 1º Bimestre – Sistemas III – Dilatação, Calorimetria e Gases Ideais
Prof. Dr. Cláudio S. Sartori
13. A Lei do deslocamento de Wien é
obtida, impondo-se
T
0
Para:
T
8 hc
d
1
5
e
hc
kT
d
1
Utilizando a Lei do deslocamento de Wien:
max
2.898
mm K
T
Ache a que temperatura corresponde ao máximo
comprimento de max = 305 nm.
16. A temperatura superficial do Sol é cerca de
(b) Aplicando a Lei de Stefan-Boltzman:
6000K.
4
H A e
T
(a) Se admitirmos que o Sol irradia como um
: constante de Stefan-Boltzmann.
corpo
negro,
em que comprimento de onda max se
2
5.6699 10 8 WKm4
localizará o máximo da distribuição espectral?
Encontre a potência dissipada nessa temperatura,
(b) Calcular max para um corpo negro a
assumindo área 20 cm2 e emissividade e = 1;
temperatura ambiente, cerca de 300 K.
14. Duas barras metálicas, cada qual com 5
cm de comprimento e seção reta retangular de 2 cm
por 3 cm, estão montadas entre duas paredes, uma
mantida a 100 0C e outra a 0 0C. Uma barra é de
chumbo (Pb) e a outra é de prata (Ag). Calcular:
(a) A corrente térmica através das barras.
(b) a temperatura da superfície de contato das
duas.
Dado: Condutividades térmicas:
Pb = 353 W/(m.K)
Ag = 429 W/(m.K)
17. Calcular a perda de energia líquida de uma
pessoa nua numa sala a 200C, admitindo que irradie
como um corpo negro de área superficial igual a 1.4 m2,
na temperatura de 33 0C. A temperatura superficial do
corpo humano é ligeiramente mais baixa que a
temperatura interna de 370C, em virtude da resistência
térmica da pele.
18. Na prática de construção civil, nos países
de língua inglesa, especialmente nos Estados Unidos, é
costume utilizar o fator R, simbolizado por Rf, que é a
resistência térmica por pé quadrado do material. Assim,
o fator R é igual ao quociente entre a espessura do
material e a condutividade térmica:
Rf
e
R A
A tabela ilustra os fatores de R para alguns
materiais de construção.
Tabela 1 – Fatores R para alguns materiais de
construção.
e
15. As duas barras do exemplo anterior são
montadas como ilustra a figura a seguir. Calcular:
(a) A corrente térmica em cada barra
metálica.
(b) A corrente térmica total.
(c) A resistência térmica equivalente desta
montagem.
Rf
Material
(in)
Chapas divisórias
Gesso ou estuque
Compensado
(pinho)
Painéis de madeira
Carpetes
Isolamento de teto
0.375
(h.ft2.F/Btu)
0.32
0.5
0.62
0.75
1.0
1.0
0.93
2.08
2.8
Manta asfáltica
1.0
0.15
Chapas de madeira
asfáltica
1.0
0.44
6
6
Lista de Exercícios - 1º Bimestre – Sistemas III – Dilatação, Calorimetria e Gases Ideais
Prof. Dr. Cláudio S. Sartori
Um telhado de 60 ft por 20 ft é feito de chapa
22. – O espectro típico de uma lâmpada
de pinho, de 1 in, cobertas por chapas de madeira fluorescente está indicado abaixo:
asfáltica.
(a) Desprezando a superposição das chapas de
madeira, qual a taxa de condução de calor através do
telhado, quando a temperatura no interior da
edificação for de 70 0F e no exterior 40 F ?
(b) Calcular a taxa de condução de calor se à
cobertura anterior forem superpostas 2 in de
isolamento especial para telhados.
19. A equação:
F
A
(a) Utilizando a Lei do deslocamento de Wien:
Y
T
Fornece a tensão necessária para manter a
temperatura da barra constante à medida que a
temperatura varia. Mostre que se o comprimento
pudesse variar de ΔL quando sua temperatura varia de
ΔT, a tensão seria dada por:
F
A Y
L
L0
T
Onde:
F: tensão na barra.
L0: comprimento original da barra.
Y: Módulo de Young.
Α: coeficiente de dilatação linear.
2.898
mm K
T
max
7
Ache a que temperatura corresponde ao máximo
comprimento de onda dessas lâmpadas. Observe que o
pico em comprimento de onda ocorre para essas
lâmpadas em torno de max = 305 nm.
(b) Aplicando a Lei de Stefan-Boltzman:
H
T4
A e
: constante de Stefan-Boltzmann.
5.6699 10
8 W m2
K4
Encontre a potência dissipada nessa temperatura,
assumindo área 20 cm2 e emissividade e = 1;
23. – As lâmpadas UV fluorescentes são
usualmente categorizadas como lâmpadas UVA, UVB
ou UVC, dependendo da região em que maior parte de
20. Uma placa quadrada de aço de 10 cm de sua irradiação se situa. O espectro UV está dividido
lado é aquecida em uma forja de ferreiro até 1000C. Se dentro de três regiões:
Região UVA, 315 a 400 nanômetros;
sua emissividade é e = 0.60, qual será a taxa total de
Região UVB, 280 a 315 nanômetros;
energia emitida por radiação ?
Região UVC, abaixo de 280 nanômetros.
Complete a relação da tabela.
21 - Determine:
(a) As resistências térmicas do cobre, do aço
e a equivalente.
Região
f
E
(b) O fluxo de calor através da barra de cobre
0
(Hz)
(eV)
(A)
de seção quadrada da figura. A temperatura na
interface.
> 109
< 3 x 109
< 10-5
UVA
Dados: condutividade térmica:
cobre: Cu 385,0 J(s m°C)-1
109 -1
10-5 - 0.01
UVB
aço: Aço 50,2 J(s m°C)
106
dQ
dt
R
A T
e
106 7000
UVC
e
3 x 1012
- 4.3 x
1014
A
4.3 x
1014 7.5 x
1014
Visível
Dados: f
c ; E h f h 6,62 10
c= 3.108m/s;
E eV
2-3
34
J s ;
1240
nm
7
Lista de Exercícios - 1º Bimestre – Sistemas III – Dilatação, Calorimetria e Gases Ideais
Prof. Dr. Cláudio S. Sartori
24. – Se colocarmos as barras indicadas numa
ligação em paralelo encontre a resistência térmica
equivalente e o fluxo total de calor.
Teoria cinética dos gases
1. – Qual volume ocupado por um mol de gás
perfeito?
n R T
P
2. – Calcule: (a) o número de moles n e (b) o
número de moléculas N em 2 cm3 de certo gás a 0°C e
1 atm de pressão.
Dado:
PV
N
Dados: condutividade térmica:
cobre: Cu 385,0 J(s m°C)-1
aço:
Aço
n R T
V
n NA
N A 6.02 1023
3. – Uma certa massa de gás tem o volume de
2 L a 30°C na pressão de 1.2 atm. Se o volume do gás
for reduzido para 1.5L e aquecido a 60°C, qual sua
nova pressão?
50,2 J(s m°C)-1
4. – Quantos moles de gás estão na amostra
mencionada neste exemplo?
dQ
dt
5. – A massa molecular do hidrogênio é 1.008
g/mol. Qual a massa de um átomo de hidrogênio?
R
A T
e
e
A
25. – Explique o mecanismo das brisas
oceânicas.
Dado: m
M
NA
6. – A massa do oxigênio gasoso (O2) é cerca
de 32 g/mol e a do hidrogênio gasoso (H2) é cerca de
2g/mol. Calcular:
(a) A velocidade média quadrática das
moléculas de oxigênio quando a temperatura for de 290
K.
(b) A velocidade média quadrática das
moléculas de hidrogênio quando a temperatura for de
290 K.
Dado:
vmqO
2
3RT
M
7. – Um cubo de alumínio, de 10 cm de lado, é
aquecido de 10°C a 30°C. Qual a variação de seu
26. – Determine o comprimento da barra volume? E da sua densidade?
indicado para que o fluxo de calor seja de 250W.
8. – Um calorímetro de cobre de 100 g de
massa contém 150 g de água e 8 g de gelo, em
equilíbrio térmico a pressão atmosférica. Colocam-se
no calorímetro 100 g de chumbo à temperatura de
200°C. Achar a temperatura final se não houver perda
de calor para o meio ambiente.
8
8
Lista de Exercícios - 1º Bimestre – Sistemas III – Dilatação, Calorimetria e Gases Ideais
Prof. Dr. Cláudio S. Sartori
Espectros de estrelas
(Adaptado de:
http://docs.kde.org/stable/pt_BR/kdeedu/kstars/aicolorandtemp.html)
As estrelas parecem ser exclusivamente
brancas a primeira vista. Mas se olharmos
cuidadosamente, podemos notar uma faixa de cores:
azul, branco, vermelho e até dourado. Na constelação
de Orion, um bonito contraste é visto entre o vermelho
de Betelgeuse no "sovaco" de Orion e o azul de
Bellatrix no ombro. O que faz estrelas exibirem cores
diferentes permanecia um mistério até dois séculos
atrás,
quando
físicos
obtiveram
suficiente
conhecimento da natureza da luz e propriedades da
matéria em temperaturas imensamente altas.
Especificamente, foi a física da radiação dos
corpos negros que nos possibilitou entender a variação
das cores estelares. Logo após o entendimento do que
era a radiação dos corpos negros, notou-se que o
espectro das estrelas parecia extremamente similar as
curvas da radiação dos corpos negros em várias
temperaturas, variando de poucos milhares de Kelvin
até 50.000 Kelvin. A conclusão óbvia é que estrelas
são semelhantes a corpos negros, e que a variação de
cor das estrelas é uma consequência direta da
temperatura de sua superfície.
Estrelas frias (isto é, Espectro Tipo K e M)
irradiam a maior parte de sua energia na região
vermelha
e
infravermelha
do
espectro
electromagnético e assim parecem vermelhas,
enquanto estrelas quentes (isto é, Espectro Tipo O e B)
emitem principalmente em comprimentos de onda azul
e ultravioleta, fazendo-as parecerem azul ou brancas.
Para estimar a temperatura superficial de uma
estrela, podemos usar a conhecida relação entre
temperatura de um corpo negro e o comprimento de
onda da luz no pico de seu espectro. Isto é, conforme
você aumenta a temperatura de um corpo negro, o pico
de seu espectro move-se para um menor (mais azul)
comprimento de onda luminoso. Isto é ilustrado na
Figura 1 abaixo onde a intensidade de três estrelas
hipotéticas é plotada contra o comprimento de onda. O
"arco-íris" indica a faixa de comprimento de onda que
é visível ao olho humano.
Figura 1 – Espectro de estrelas de diferentes cores.
Este método simples é conceitualmente
correto, mas não pode ser usado para obter
temperaturas estelares precisas, porque estrelas não são
corpos negros perfeitos. A presença de vários
elementos na atmosfera estelar fará com que alguns
comprimentos de onda sejam absorvidos.
Devido a estas linhas de absorção não serem
uniformemente distribuídas no espectro, elas podem
inclinar a posição do pico espectral. Além disso, obter
um espectro estelar é um processo de tempo intensivo e
é proibitivamente difícil para grandes amostras de
estrelas.
Um método alternativo utiliza a fotometria
para medir a intensidade da luz passando por diferentes
filtros. Cada filtro permite apenas uma parte específica
do espectro passar enquanto todas as outras são
rejeitadas. Um sistema fotométrico muito utilizado
chama-se sistema UBV Johnson. Ele emprega três
filtros de banda: U ("Ultra-violeta"), B ("Azul"), and V
("Visível"), cada uma ocupando as diferentes regiões
do espectro eletromagnético.
O processo de fotometria UBV envolve usar
dispositivos foto sensíveis (como filmes ou câmeras
CCD) e mirar um telescópio em uma estrela para medir
a intensidade da luz que passa por cada filtro
individualmente.
Este
processo
fornece
três
luminosidades aparentes ou fluxos (quantidade de
energia por cm2 por segundo) designados por Fu, Fb e
FV. A relação dos fluxos Fu/Fb e Fb/Fv é uma medida
quantitativa da "cor" da estrela, e estas relações podem
ser usadas para estabelecer uma escala de temperatura
para estrelas. Falando genericamente, quanto maiores
as relações Fu/Fb e Fb/Fv de uma estrela, mais quente é
sua temperatura de superfície.
Por exemplo, a estrela Bellatrix em Orion tem
um Fb/Fv = 1,22, indicando que é mais brilhante pelo
filtro B que pelo filtro V. Além disso, sua razão Fu/Fb é
2,22, então é mais brilhante pelo filtro U. Isto indica
que a estrela deve ser muito quente mesmo, pois seu
pico espectral deve estar em algum lugar na faixa do
filtro U, ou até mesmo em comprimentos de onda mais
baixos. A temperatura superficial de Bellatrix
(determinada por comparação de seu espectro com
modelos detalhados que conferem com suas linhas de
absorção) é perto de 25.000 Kelvin.
Podemos repetir esta análise para a estrela Betelgeuse.
Suas razões Fb/Fv e Fu/Fb são 0.15 e 0.18
respectivamente, então ela é mais brilhante em V e
mais opaca em U. Então, o pico espectral de Betelgeuse
deve estar em algum lugar na faixa do filtro V, ou
mesmo em um comprimento de onda superior. A
temperatura superficial de Betelgeuse é de apenas 2,400
Kelvin.
Os astrônomos preferem expressar as cores
estelares em termos de diferença em magnitudes, do
que uma razão de fluxos. Assim, voltando para a azul
Bellatrix temos um índice de cor igual a
B - V = -2.5 log (Fb/Fv) = -2.5 log (1.22) = -0.22,
Similarmente, o índice de cor para a vermelha
Betelgeuse é
B - V = -2.5 log (Fb/Fv) = -2.5 log (0.18) = 1.85
9
9
Lista de Exercícios - 1º Bimestre – Sistemas III – Dilatação, Calorimetria e Gases Ideais
Prof. Dr. Cláudio S. Sartori
Os índices de cores, como a escala de
magnitude ,correm para trás. Estrelas Quentes e
azuis têm valores de B-V menores e negativos que as
mais frias e vermelhas estrelas.
Um Astrônomo pode então usar os índices de
cores para uma estrela, após corrigir o
avermelhamento e extinção interestelar, para obter
uma precisa temperatura daquela estrela. A relação
entre B-V e temperatura é ilustrada na Figura 2.
Figura 2 – Relação B-V e temperatura.
10
Pirômetros
Um pirómetro (também denominado de
pirómetro óptico) é um dispositivo que mede
temperatura sem contacto com o corpo/meio do qual
se pretende conhecer a temperatura. Geralmente este
termo é aplicado a instrumentos que medem
temperaturas superiores a 600 graus celsius. Uma
utilização típica é a medição da temperatura de metais
incandescentes em fundições.
Um dos pirómetros mais comuns é o de
absorção-emissão, que é utilizado para determinar a
temperatura de gases através da medição da radiação
emitida por uma fonte de referência, antes e depois da
radiação incidir sobre o gás (que absorve parte da
radiação). É através da análise das diferenças do
espectro do gás que se consegue determinar a sua
temperatura. Ambas as medições são feitas no mesmo
intervalo de comprimento de onda.
Outra aplicação típica do pirómetro é a
medição da temperatura de metais incandescentes.
Olhando pelo visor do pirómetro observa-se o metal,
ajustando-se depois manualmente a corrente elétrica
que percorre um filamento que está no interior do
pirómetro e aparece no visor. Quando a cor do
filamento é idêntica à do metal, pode-se ler a
temperatura numa escala disposta junto ao elemento de
ajuste da cor do filamento.
10
Lista de Exercícios - 1º Bimestre – Sistemas III – Dilatação, Calorimetria e Gases Ideais
Prof. Dr. Cláudio S. Sartori
Descoberto por acaso o sucessor das átomos, o que é justamente o "tamanho mágico" no
qual o cristais preferencialmente se formam. Assim,
lâmpadas incandescentes
Redação do Site Inovação Tecnológica
esses minúsculos pontos quânticos são fáceis de serem
25/10/2005
produzidos, ainda que tenham apenas metade do
http://www.inovacaotecnologica.com.br/
tamanho dos pontos quânticos normais.
Quando esses pontos quânticos foram
Pegue um LED que produza uma luz azul
iluminados com um laser, ao invés da luz azul que os
intensa. Recubra-o com uma finíssima película de
estudantes esperavam, eles se encantaram com o branco
cristais microscópicos, chamados pontos quânticos, e
vivo que iluminou a mesa onde faziam seu
você terá a próxima revolução tecnológica na
experimento.
iluminação, que poderá substituir virtualmente todas as
A seguir os estudantes dissolveram seus
atuais lâmpadas.
pontos quânticos em uma espécie de verniz para
Esse LED híbrido, descoberto por acaso pelo
madeira e "pintaram" um LED. Embora isso seja o que
estudante Michael Bowers, da Universidade
se poderia chamar de uma típica uma idéia de
Vanderbilt, Estados Unidos, é capaz de emitir luz
estudante, eles estavam, na verdade, montando sua
branca verdadeira, similar à emitida pelas lâmpadas
descoberta sobre uma fonte própria de luz, dispensando
incandescentes, com uma leve tonalidade de amarelo.
o laser. O resultado não é nenhum primor de
Até agora os pontos quânticos têm recebido
acabamento, mas demonstra claramente que a junção
atenção graças à sua capacidade de produzir dezenas
dos dois pode gerar uma nova fonte de luz branca que
de cores diferentes simplesmente variando-se o
poderá revolucionar todo o setor de iluminação.
tamanho dos nanocristais individuais: uma capacidade
A descoberta foi descrita em um artigo
particularmente adequada à marcação fluorescente de
publicado no exemplar de 18 de Outubro do Jornal da
células em aplicações biomédicas.
Sociedade Americana de Química.
Mas os cientistas agora descobriram uma
nova forma para construir pontos quânticos capazes de
produzir espontaneamente luz branca de largo
espectro.
Até 1993 os LEDs só produziam luzes
vermelha, verde e amarela. Foi então que o
pesquisador japonês Isamu Akasaki descobriu como
fabricar LEDs que emitiam luz azul. Combinando
LEDs azuis com outros verdes e vermelhos - ou
adicionando-se fósforo amarelo aos LEDs azuis - os
fabricantes conseguiram criar luz branca, o que abriu
uma gama totalmente nova de aplicações para essas
fontes de luz, por natureza extremamente econômicas
e duráveis. Mas a luz emitda pelos "LEDs brancos" é
apenas ligeiramente branca, apresentando um forte
tom azulado.
Os pontos quânticos de luz branca, por outro
lado, produzem uma distribuição mais suave dos
comprimentos de onda do espectro visível, com uma
leve tonalidade amarela. Desta forma, a luz produzida
pelos pontos quânticos se parece mais com as luzes de
"espectro total" utilizadas para leitura, um tipo de
lâmpada disponível no mercado que produz uma luz
com um espectro mais próximo ao da luz do Sol do
que as lâmpadas incandescentes ou fluorescentes.
Além disso, os pontos quânticos, como
acontece também com os LEDs, têm a vantagem de
não emitir grandes quantidades de luz infravermelha,
como acontece com as lâmpadas incandescentes. Essa
radiação invisível produz grandes quantidades de calor
e é responsável pela baixa eficiência energética desse
tipo de lâmpada.
Bowers estava estudando com seu colega
James McBride, procurando entender como os pontos
quânticos crescem. Para isso eles estavam tentando
criar pontos quânticos cada vez menores. Foi então
que eles criaram um lote desses nanocristais de cádmio
e selênio. Esses elementos contêm 33 ou 34 pares de
11
11
Lista de Exercícios - 1º Bimestre – Sistemas III – Dilatação, Calorimetria e Gases Ideais
Prof. Dr. Cláudio S. Sartori
12
12