Introdução à Programação Aula 23 — Aritmética com racionais

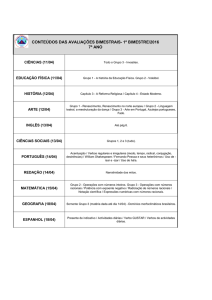
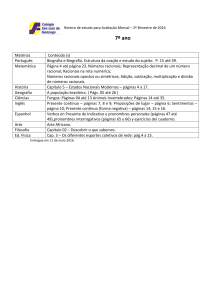
Nesta aula
Introdução à Programação
Aula 23 — Aritmética com racionais
1
Aritmética com racionais
2
Soma e multiplicação
3
Simplificação
4
Comparações
Pedro Vasconcelos
DCC/FCUP
2013
Pedro Vasconcelos (DCC/FCUP)
Introdução à Programação Aula 23 — Aritmética com racionais
2013
1 / 28
Nesta aula
1
2
4
Comparações
Pedro Vasconcelos (DCC/FCUP)
2013
2 / 28
2013
4 / 28
Em Python temos tipos numéricos primitivos inteiros e
vírgula-flutuante
Vamos implementar um novo tipo de dados para números
racionais (frações):
Soma e multiplicação
Simplificação
Introdução à Programação Aula 23 — Aritmética com racionais
Aritmética com racionais
Aritmética com racionais
3
Pedro Vasconcelos (DCC/FCUP)
1 2
5
+ =
2 3
6
5 3
5
× =
6 4
8
Plano:
uma nova classe Fraction para representar frações
métodos para soma, multiplicação e comparações
implementados usando apenas operações inteiras
não há erro de arredondamento
Introdução à Programação Aula 23 — Aritmética com racionais
2013
3 / 28
Números racionais
Pedro Vasconcelos (DCC/FCUP)
Introdução à Programação Aula 23 — Aritmética com racionais
Em Python
class Fraction:
"Classe para aritmética com números racionais."
def __init__(self, num, denom):
if denom==0:
raise ZeroDivisionError("denominador zero")
self.num = num
self.denom = denom
Um número racional p/q é composto por:
um numerador p ∈ Z;
um denominador q ∈ Z \ {0}
Um par (p, q) define um número racional p/q
Pares diferentes podem representar o mesmo número racional;
por ex.: (2, 3), (4, 6) e (6, 9) representam 2/3
def __str__(self):
return "%d/%d" % (self.num,self.denom)
Pedro Vasconcelos (DCC/FCUP)
Introdução à Programação Aula 23 — Aritmética com racionais
2013
5 / 28
Nesta aula
1
2
Pedro Vasconcelos (DCC/FCUP)
p
r
p×s
q×r
+ =
+
q s
q×s q×s
Soma e multiplicação
=
Simplificação
4
Comparações
Pedro Vasconcelos (DCC/FCUP)
2013
6 / 28
2013
8 / 28
Somar e multiplicar frações
Aritmética com racionais
3
Introdução à Programação Aula 23 — Aritmética com racionais
(denominador comum)
p×s+q×r
q×s
p
r
p×r
× =
q s
q×s
Introdução à Programação Aula 23 — Aritmética com racionais
2013
7 / 28
Pedro Vasconcelos (DCC/FCUP)
Introdução à Programação Aula 23 — Aritmética com racionais
Em Python
Exemplos
class Fraction:
.
.
.
def __add__(x, y):
r = Fraction(x.num*y.denom + x.denom*y.num,
x.denom*y.denom)
return r
>>> print(Fraction(1,2) + Fraction(1,3))
5/6
>>> print(Fraction(1,2) + Fraction(1,2))
4/4
>>> print(Fraction(5,6) * Fraction(3,4))
15/24
Mas:
def __mul__(x, y):
r = Fraction(x.num*y.num, x.denom*y.denom)
return r
Pedro Vasconcelos (DCC/FCUP)
Introdução à Programação Aula 23 — Aritmética com racionais
1
4
=
4
1
15
3×5
5
=
=
24
3×8
8
Os resultados não estão simplificados. . .
2013
9 / 28
Nesta aula
Pedro Vasconcelos (DCC/FCUP)
Introdução à Programação Aula 23 — Aritmética com racionais
2013
Simplificar fracções
1
Aritmética com racionais
2
Soma e multiplicação
3
Simplificação
Se p e q não têm divisor comum maior que a unidade, p/q é uma
fração irredutivel.
4
Comparações
Logo: vamos dividir p e q pelo seu maior divisor comum.
Pedro Vasconcelos (DCC/FCUP)
Introdução à Programação Aula 23 — Aritmética com racionais
Podemos simplificar uma fração p/q se existir um divisor d comum a p
e q:
p
p0 × d
p0
p = p0 × d
=⇒
= 0
= 0
0
q =q ×d
q
q ×d
q
2013
11 / 28
Calcular o máximo divisor comum
mdc(a, 0) = a
Permitem calcular o máximo divisor comum: definem um algoritmo.
2013
13 / 28
Usar o MDC para simplificar frações
Modificamos o inicializador para simplificar usando o mdc
Todos os métodos que criam frações devem usar o inicializador
Introdução à Programação Aula 23 — Aritmética com racionais
2013
12 / 28
Pedro Vasconcelos (DCC/FCUP)
Introdução à Programação Aula 23 — Aritmética com racionais
2013
14 / 28
Inicializador revisto
Queremos garantir que as frações são sempre irredutíveis
Pedro Vasconcelos (DCC/FCUP)
Introdução à Programação Aula 23 — Aritmética com racionais
def mdc(a, b):
"Calcula o máximo divisor comum de a,b."
while b != 0:
r = a%b
a = b
b = r
# fim do ciclo
return a
mdc(a, b) = mdc(b, resto da divisão de a por b)
Introdução à Programação Aula 23 — Aritmética com racionais
Pedro Vasconcelos (DCC/FCUP)
Algoritmo de Euclides em Python
Duas propriedades do máximo divisor comum:
Pedro Vasconcelos (DCC/FCUP)
10 / 28
2013
15 / 28
class Fraction:
def __init__(self, num, denom):
if denom==0:
raise ZeroDivisionError("denominador zero")
d = mdc(num, denom)
self.num = num//d
self.denom = denom//d
.
.
.
Pedro Vasconcelos (DCC/FCUP)
Introdução à Programação Aula 23 — Aritmética com racionais
2013
16 / 28
Exemplos
Frações negativas
Como representar frações negativas?
>>>
2/3
>>>
1/1
>>>
5/8
>>>
7/4
print(Fraction(4,6))
−
print(Fraction(1,2) + Fraction(1,2))
print(Fraction(5,6) * Fraction(3,4))
2
(−2)
2
=
=
3
3
(−3)
Convenção
print((Fraction(2,3)+Fraction(1,2))*Fraction(3,2)) Na representação de p/q temos sempre q > 0 (i.e. o sinal está
sempre no numerador).
Pedro Vasconcelos (DCC/FCUP)
Introdução à Programação Aula 23 — Aritmética com racionais
2013
17 / 28
Frações negativas
Introdução à Programação Aula 23 — Aritmética com racionais
2013
18 / 28
2013
20 / 28
Exemplos
class Fraction:
def __init__(self, num, denom):
if denom==0:
raise ZeroDivisionError("denominador zero")
if denom<0:
denom = -denom
num = -num
d = mdc(num, denom)
self.num = num//d
self.denom = denom//d
.
.
.
Pedro Vasconcelos (DCC/FCUP)
Pedro Vasconcelos (DCC/FCUP)
Introdução à Programação Aula 23 — Aritmética com racionais
2013
19 / 28
Nesta aula
>>> print(Fraction(2,-3))
-2/3
>>> print(Fraction(-4,-3))
4/3
>>> print(Fraction(1,2) + Fraction(1,-2))
0/1
Pedro Vasconcelos (DCC/FCUP)
Introdução à Programação Aula 23 — Aritmética com racionais
Operadores de comparação
1
Aritmética com racionais
2
Soma e multiplicação
3
Simplificação
4
Comparações
Pedro Vasconcelos (DCC/FCUP)
Podemos definir operadores de comparação para objetos usando os
seguintes métodos:
==
!=
<
>
<=
>=
Introdução à Programação Aula 23 — Aritmética com racionais
2013
21 / 28
Comparação de frações
Pedro Vasconcelos (DCC/FCUP)
__eq__
__ne__
__lt__
__gt__
__ge__
__le__
Introdução à Programação Aula 23 — Aritmética com racionais
2013
22 / 28
2013
24 / 28
Generalizando
Quando é p/q é menor que r /s?
p
r
p
r
<
⇐⇒
− <0
q
s
q s
⇐⇒
⇐⇒
p
r
<
⇐⇒ p × s < q × r
q
s
p×s
q×r
−
<0
q×s q×s
p
r
=
⇐⇒ p × s = q × r
q
s
p×s−q×r
<0
q×s
⇐⇒ p × s − q × r < 0
(assumindo q > 0, s > 0)
⇐⇒ p × s < q × r
Pedro Vasconcelos (DCC/FCUP)
Introdução à Programação Aula 23 — Aritmética com racionais
2013
23 / 28
Pedro Vasconcelos (DCC/FCUP)
Introdução à Programação Aula 23 — Aritmética com racionais
Em Python
Em Python (cont.)
class Fraction:
.
.
.
def __eq__(x, y):
return x.num*y.denom == x.denom*y.num
É suficiente definirmos __eq__, __lt__ e __le__:
def __lt__(x, y):
return x.num*y.denom < x.denom*y.num
x 6= y
⇐⇒
¬(x = y )
x >y
⇐⇒
y <x
x ≥y
⇐⇒
y ≤x
def __le__(x,y):
return x.num*y.denom < x.denom*y.num
Pedro Vasconcelos (DCC/FCUP)
Introdução à Programação Aula 23 — Aritmética com racionais
2013
25 / 28
Exemplos
Introdução à Programação Aula 23 — Aritmética com racionais
2013
26 / 28
Sumário
Definimos nesta aula:
>>> Fraction(1,3) < Fraction(1,2)
True
>>> Fraction(1,2) < Fraction(1,3)
False
>>> Fraction(5,6) == Fraction(1,2)+Fraction(1,3)
True
Pedro Vasconcelos (DCC/FCUP)
Pedro Vasconcelos (DCC/FCUP)
Introdução à Programação Aula 23 — Aritmética com racionais
2013
Um novo tipo de dados para números racionais (frações)
Operações para soma, multiplicação e comparação
A sobrecarga permite usar os operadores usuais (+, *, <, ==)
Exercícios: implementar subtração, divisão, operações mistas
com frações e inteiros
27 / 28
Pedro Vasconcelos (DCC/FCUP)
Introdução à Programação Aula 23 — Aritmética com racionais
2013
28 / 28