Roteiro Laboratório Fisica II

Centro Universitário UNICAPITAL e
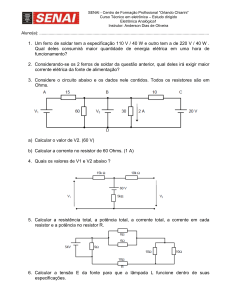
Faculdades Integradas Paulista FIP
Engenharia de Automação e Controle
Engenharia Elétrica
Engenharia Mecânica
Engenharia Civil
Roteiro para
Laboratório de Física 2
Experiência 01
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
Estag. Eriki Masahiko Takara
Laboratorista Vivian Delacoleta
São Paulo 2014
Instruções para a elaboração do Relatório
Após a realização do experimento pelo grupo deve ser apresentado ao professor
responsável um relatório que deverá ser elaborado em grupo, contendo os itens
relacionados a seguir.
Além da apresentação dos dados tomados no laboratório, o relatório deverá conter o
tratamento destes dados bem como sua análise, conforme as instruções sobre o
detalhamento da análise de dados fornecidas neste roteiro.
1. Capa: folha de rosto com a identificação do número do experimento, título, data da
realização do experimento, unidade e turma, sendo que estas informações podem
ser dispostas numa tabela como segue:
Número do Experimento
Título
Data do Experimento
Unidade
Turma
RA
Nome Completo
Assinatura
1
2
3
4
5
6
2. Objetivo: descreva resumidamente qual(is) o(s) objetivo(s) a ser(em) atingido(s)
com o experimento.
3. Material Utilizado: relacione em itens os materiais utilizados no experimento,
citando a identificação técnica (modelo e marca) dos equipamentos e dispositivos
elétricos/eletrônicos, podendo ilustrar com figuras, fotos ou diagramas.
4. Procedimento Experimental: descrição resumida do procedimento adotado para a
realização do experimento.
5. Dados: mostre claramente os dados obtidos, relacionando-os numa tabela, quando
possível.
6. Análise dos Dados: descreva explicitamente os cálculos feitos com os dados
obtidos e outras análises realizadas com os dados colhidos; mostre os resultados
obtidos com os cálculos em tabelas e gráficos quando pertinentes
7. Conclusão: elabore um ou mais parágrafos sobre o que pôde ser concluído a partir
dos dados obtidos e sua análise
8. Referências Bibliográficas: apresente a bibliografia consultada nos estudos
realizados.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
1
SP 04/05/14 (v9s)
Parte prática Laboratórios
Este laboratório será dividido em 3 partes, cada qual com um objetivo de aprendizado
específico que será explicado posteriormente.
A lista de material utilizado a seguir refere-se a todas as partes.
Materiais necessários a realização da sequência de experimentos (vide anexo 5):
1.
2.
3.
4.
5.
Resistores de diversos valores superiores a 1000 Ω;
Multímetro;
Fonte de tensão e corrente contínuas até 30 Vcc;
Proto-board;
Cabos e fios para montagem dos circuitos.
Parte 1
Título: LEITURA E MEDIÇÃO DA RESISTÊNCIA ELÉTRICA DE RESISTORES
Objetivos:
1. Iniciar o contato com o instrumento de medição de resistência elétrica, tensão e
corrente, fazendo medidas preliminares de resistência elétrica.
2. Ler valor nominal da resistência do resistor pelo código de cores.
3. Ler e calcular a tolerância de um resistor e definir se este enquadra-se dentro da
faixa de tolerância.
Introdução Teórica para realização do experimento e análise dos dados obtidos:
Valor Nominal
Valor nominal é o valor da grandeza física do dispositivo que é informado pelo seu
fabricante, por exemplo, no caso dos resistores, o valor nominal é aquele lido no corpo
do resistor a partir da tabela de cores.
Critérios de Arredondamento
Ao ser realizada uma medida necessariamente devemos respeitar as imprecisões dos
instrumentos envolvidos na média, fazendo ajustes, desprezando as casas decimais
que estão fora da precisão desejada. Esta operação é denominada Arredondamento.
A norma técnica ABNT/NBR 5891/1977, detalhada no anexo 2, estabelece os critérios
de arredondamento que devem ser utilizados na elaboração de cálculos e médias que
assim as exijam. Lembrar que uma norma não é uma lei, esta necessariamente não
precisa ser aplicada se não for exigida, cabendo neste caso o bom senso do calculista.
Em nossos experimentos, para agilizarmos as medidas e cálculos, adotaremos um
critério de arredondamento simplificado, sem perda de qualidade. Tornando o critério
de arredondamento o mesmo utilizado na maioria das calculadoras cientificas.
Um número é arredondado para outro, com o número de algarismos significativos
desejados, pelo cancelamento de um ou mais algarismos da direita para a esquerda.
Duas regras são utilizadas neste caso:
1-Quando o algarismo suprimido é menor do que 5, o imediatamente anterior
permanece igual.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
2
SP 04/05/14 (v9s)
2-Quando o algarismo suprimido é maior ou igual a 5, o imediatamente anterior é
acrescido de uma unidade.
Exemplos:
Arredondar 2ª casa após a virgula: L = 2,143 m (antes) ⇒ L = 2,14 m (depois)
Arredondar 3ª casa após a virgula: L = 0,0506 m (antes) ⇒ L = 0,051 m (depois)
Arredondar 1ª casa após a virgula: L = 0,12983 m (antes) ⇒ L = 0,1 m (depois)
Arredondar para um numero inteiro: L = 1,55 m (antes) ⇒ L = 2 m (depois)
Algarismos Significativos
Na medição de grandezas físicas, além da leitura certa do valor da medida no aparelho
de medição, costuma-se fazer estimativas com aproximações de frações da menor
divisão da escala do instrumento.
Os algarismos corretos da medida mais um algarismo duvidoso (zeros à direita são
algarismos significativos e zeros à esquerda não são) são chamados de algarismos
significativos, para maiores detalhe e instruções sobre as operações com os algarismos
significativos vide anexo 3.
Resistores - Tabela de cores
A tabela de cores mostra o padrão adotado para o código que relaciona os valores de
resistência dos resistores e cores que são gravadas em seu corpo.
No anexo 1, apresentamos uma tabela de cores com instrução de como decodificá-las
para encontrar o valor nominal de resistência do resistor e uma abordagem sobre a
quantidade de faixas dos resistores, indicativo de sua precisão.
O que é Tolerância?
A tolerância de um dispositivo elétrico ou eletrônico representa uma faixa de valores
dentro da qual o valor real deste dispositivo permite seu funcionamento adequado
quando inserido num sistema ou circuito.
Por exemplo, se tivermos um resistor com tolerância de 5% e seu valor nominal é de
300 Ω, a faixa de tolerância está entre 275 Ω e 315 Ω, ou seja, ao medirmos o valor de
sua resistência (valor real), ele deverá se encontrar dentro desta faixa: se o valor
medido (real) for 320 Ω, o resistor estará inadequado para uso, pois, o valor de sua
resistência está acima do limite máximo de tolerância.
Usualmente indicamos a faixa de tolerância referenciando o valor nominal com os
limites mínimos e máximos ao lado:
Rnominal = ( 300 ± 15 ) Ω
Ligação de multímetro para medição de resistência de resistores
Para a ligação do multímetro como ohmímetro para medição da resistência dos
resistores, vide anexo 5.
Instruções para a realização do experimento:
1. Faça a leitura do valor da resistência dos resistores fornecidos, utilizando a tabela
de cores de resistores que se encontra no anexo 1 deste roteiro. Este valor lido é o
valor nominal de resistência do resistor.
2. Leia também a tolerância e anote junto com o valor de resistência de cada resistor.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
3
SP 04/05/14 (v9s)
3. Regule o multímetro para uma escala adequada para os valores lidos
lido de
resistência dos resistores, vide Anexo 5.
4. Posicione o resistor na proto
proto-board
board adequadamente (veja esquema de ligação da
proto-board
board no anexo 5).
5. Meça a resistência dos resistores, ligando
ligando-o em
paralelo com o resistor conforme a figura ao lado:
6. Tabele esses resultados, junto com os respectivos valores de resistência lidos
anteriormente.
Instruções para a análise dos dados do experimento
experimento:
1. Com
om a tolerância e o valor nominal da resistência lidos no corpo do resistor, ccalcule
os valores máximo e mínimo de aceitação do valor da resistência
esistência, obtendo assim a
faixa de tolerância.
Observação importante:: a faixa de tolerância deve ser calculada com o valor de
resistência LIDO e não com o valor MEDIDO pelo multímetro.
2. Faça uma tabela com os valores de resistência nominal (lida no corpo do resistor),
tolerância (percentual), faixa de tolerância (em ohms) e resistência medida com o
multímetro, a seguir uma sugestão de tabela.
tabela
1-Resistência
Lida (Ω)
2-Tolerância
(%)
Faixa de tolerância
da Resistor
3-Mínimo
(Ω)
4-Máximo
(Ω)
5-Resistência
Resistência
Medida
(Ω)
Ω)
6-Possível sua
utilização
(S/N)
Resistor 1
Resistor 2
Resistor 3
Resistor 4
Resistor 5
Tabela de resistores utilizados
3. Compare os valores medidos com a faixa de tolerância da resistência,
resistência classificandoos como possíveis de serem utilizados ou não num circuito.
circuito
4. Comente na conclusão d
do relatório qual a finalidade de se saber a tolerância de um
resistor e sua importância.
importância
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
4
SP 04/05/14 (v9s)
Parte 2
Título: MEDIÇÃO DE RESISTÊNCIA EQUIVALENTE DE ASSOCIAÇÃO DE
RESISTORES EM SÉRIE, PARALELA E MISTA
Objetivos:
1. Medir com o multímetro os valores de resistência equivalente de uma associação de
resistores ligados em:
o Série
o Paralelo
o Misto
2. Calcular a resistência equivalente de cada associação de resistores montada
anteriormente com os valores nominais de resistência.
3. Comparar o valor da resistência equivalente obtido do cálculo nominal (item anterior)
com o valor medido com o multímetro.
Introdução Teórica para realização do experimento e análise dos dados obtidos:
Tipos de associação de resistores
De acordo com cada finalidade, os resistores podem ser ligados diferentemente num
circuito elétrico/eletrônico.
A representação dos resistores e fonte de alimentação segue um padrão de símbolos
(vide anexo 5).
A seguir apresentamos os diversos tipos de ligação.
o Série: nesta ligação, os resistores estão ligados um após o outro de forma que a
corrente elétrica proveniente da fonte de alimentação passe por cada resistor e
circule pelo circuito sem mudança de valor. Para representarmos esta ligação,
desenhamos os resistores, com a indicação dos valores ou uma referência, ligados
como nos esquemas a seguir.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
5
SP 04/05/14 (v9s)
o Paralelo: nesta ligação, os resistores estão ligados de forma que a ddp entre os
terminais dos resistores ligados num mesmo ponto seja a mesma. Para
representarmos esta ligação, desenhamos os resistores, com a indicação dos
valores ou uma referência, ligados como nos esquemas a seguir.
o Misto: nesta ligação, os resistores estão ligados em série e em paralelo num
mesmo circuito.
O que é resistência equivalente
Quando associamos mais de um resistor, a resistência que enxergamos desse circuito
é chamada de resistência equivalente, ou seja, podemos trocar todos os resistores
associados por um único resistor de valor equivalente ao conjunto.
Cálculo de resistência equivalente
o Série
⋯ o Paralelo
⋯
Instruções para a realização do experimento:
Se os resistores utilizados para a realização da PARTE 2 do experimento forem os
mesmos de quando realizada a PARTE 1 do experimento pule para o passo 5.
1. Faça a leitura do valor nominal da resistência dos resistores fornecidos, utilizando a
tabela de cores de resistores que se encontra no anexo 1 deste roteiro.
2. Leia também a tolerância e calcule a faixa de tolerância de cada resistor.
3. Regule o multímetro para uma escala adequada para os valores lidos de resistência
dos resistores, vide anexo 5.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
6
SP 04/05/14 (v9s)
4. Meça a resistência dos resistores, tabelando esses resultados.
5. Compare os valores medidos com a faixa de tolerância da resistência, classificandoos como possíveis de serem utilizados ou não num circuito.
6. Verifique o esquema de ligação da proto-board (vide anexo 5).
7. Faça a ligação em série somente dos resistores que passaram no teste de
aceitação (tolerância) utilizando a proto-board.
8. Meça (vide anexo 5) e anote a resistência equivalente da associação em série
obtida.
9. Desmonte a associação de resistores em série.
10. Faça agora a ligação em paralelo dos resistores que passaram no teste de
aceitação (tolerância) utilizando a proto-board.
11. Meça (vide anexo 5) e anote a resistência equivalente da associação em paralelo
obtida.
Associação em
Série
Número de resistores
____
Associação em
Paralelo
Número de resistores
Resistor Equivalente=_______ Ω
____
Tabela de resistores equivalentes
Resistor Equivalente=_______ Ω
Instruções para a análise dos dados do experimento:
1- Com os valores nominais das resistências (valor nominal é aquele LIDO no corpo
do resistor a partir da tabela de cores), calcule a resistência equivalente da
associação de resistores em série.
2- Compare o valor calculado dessa resistência equivalente com o valor da resistência
total dessa associação em série MEDIDA com o multímetro.
3- Com os valores nominais das resistências (valor nominal é aquele LIDO no corpo
do resistor a partir da tabela de cores), calcule a resistência equivalente da
associação de resistores em paralelo.
4- Compare o valor calculado dessa resistência equivalente com o valor da resistência
total dessa associação em paralelo MEDIDA com o multímetro.
5- Comente nas conclusões do seu relatório se houve alguma diferença na
comparação entre os valores da resistência equivalente:
a. LIDO e MEDIDO para cada tipo de associação de resistores (analise se a
diferença entre os valores é grande ou pequena).
b. MEDIDO da associação em série com o da associação em paralelo (analise
a grandeza da resistência equivalente para cada associação).
6- Comente e explique a que se devem estas diferenças.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
7
SP 04/05/14 (v9s)
Parte 3
Título: MEDIÇÃO DE CORRENTE E TENSÃO EM ASSOCIAÇÃO DE RESISTORES E
LEVANTAMENTO DA CURVA CARACTERÍSTICA DO RESISTOR
Objetivo:
1. Medir valores de tensão em associação de resistores em série e paralelo.
2. Medir valores de corrente em associação de resistores em série e paralelo.
3. Levantar curva característica de um resistor.Determinar a resistência elétrica de um
resistor ajustando sua curva característica pelo Método dos Mínimos Quadrados.
Introdução Teórica para realização do experimento e análise dos dados obtidos:
Introdução a Teoria dos Erros
Vide anexo 3.
Ajuste de Reta pelo Método dos Mínimos Quadrados
Vide anexo 4.
Ligação de multímetro em circuitos resistivos
O instrumento de medição, multímetro, deve ser ligado conforme a grandeza a ser lida,
tensão, corrente ou resistência elétrica, na sua respectiva modalidade (vide anexo 5).
A seguir, esquemas de ligação do multímetro numa associação em série:
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
8
SP 04/05/14 (v9s)
•
Para medição de Tensão
Associação em Série
O voltímetro nesta posição
medirá a tensão total sobre os
2 resistores R1 e R2
O voltímetro nesta posição
medirá a tensão sobre o
resistor R1
O voltímetro nesta posição
medirá a tensão sobre o
resistor R2
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
Associação em Paralelo
O voltímetro nesta posição
medirá a tensão total sobre os
2 resistores R1 e R2
O voltímetro nesta
posição medirá a tensão
sobre o resistor R1
O voltímetro nesta posição
medirá a tensão sobre o
resistor R2
9
SP 04/05/14 (v9s)
•
Para medição de Corrente
Associação em Série
O amperímetro nesta
posição medirá a corrente
total que sai da fonte
O amperímetro nesta
posição medirá a corrente
que passou pelo resistor R1
O amperímetro nesta
posição medirá a corrente
que passou pelo resistor R2
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
Associação em Paralelo
O amperímetro
medirá a corrente
total que sai da fonte
Aqui o amperímetro
medirá a corrente que
passou pelo resistor R1
Aqui o amperímetro medirá a
corrente que passou pelo
resistor R2
10
SP 04/05/14 (v9s)
Instruções para a realização do experimento:
•
Medição da Tensão e Corrente nas Associações em Série e em Paralelo
1. Verifique a tolerância de 2 resistores e veja se estão dentro da faixa e podem ser
utilizados num circuito.
2. Verifique o esquema de ligação da proto-board (vide anexo 5).
3. Conecte os dois resistores em SÉRIE na proto-board (vide introdução teórica da
parte 2).
4. Verifique o esquema de ligação da fonte de alimentação (vide anexo 5).
5. Alimente o circuito com uma tensão de 15 V (vide anexo 5).
6. Com o multímetro, meça (vide esquema de ligação na Introdução teórica anterior) e
anote:
a. Tensão total da fonte
b. Tensão em cada resistor
c. Corrente total da fonte
d. Corrente que passa em cada resistor
7. Elabore uma tabela com os valores medidos para organizar os dados tomados:
Associação em Série
Tensão (V)
Corrente (A)
Fonte (total)
Resistor 1=____ Ω
Resistor 2=____ Ω
8. Desligue a fonte de alimentação.
9. Desmonte a associação dos resistores em série.
10. Conecte os dois resistores em PARALELO na proto-board (vide introdução teórica
da parte 2).
11. Verifique o esquema de ligação da fonte de alimentação (vide anexo 5).
12. Alimente o circuito com uma tensão de 15 V (vide anexo 5).
13. Com o multímetro, meça (vide esquema de ligação na Introdução teórica anterior) e
anote:
a. Tensão total da fonte
b. Tensão em cada resistor
c. Corrente total da fonte
d. Corrente que passa em cada resistor
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
11
SP 04/05/14 (v9s)
14. Elabore uma tabela com os valores medidos de cada tipo de associação de
resistores para organizar os dados tomados:
Associação em Paralelo
Tensão (V)
Corrente (A)
Fonte (total)
Resistor 1=____ Ω
Resistor 2=____ Ω
15. Desligue a fonte de alimentação.
16. Desmonte a associação dos resistores em paralelo.
•
Levantamento da Curva Característica do Resistor
1. Monte na proto-board o circuito abaixo:
2. Regule a fonte de tensão para 20 V e ligue-a no circuito.
3. Meça a corrente que passa pelo resistor R1 com o multímetro na modalidade de
amperímetro.
4. Diminua a tensão da fonte para 19 V.
5. Meça a respectiva corrente que passa pelo resistor R1.
6. Assim sucessivamente, vá diminuindo o valor da tensão da fonte de 1 V em 1 V até
chegar no valor de 10 V; para cada valor de tensão, meça a respectiva corrente.
7. Estime uma amplitude para a incerteza nos valores das tensões aplicadas (vide
anexo 3).
8. Tabele estes dados obtidos de corrente e tensão (complete a tabela da próxima
pagina:
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
12
SP 04/05/14 (v9s)
Corrente (A)
Tensão (V)
20
19
18
17
16
15
14
13
12
11
10
± incerteza da tensão (V)
Instruções para a análise dos dados do experimento:
1. Com os dados obtidos de tensão e respectivas correntes, faça um gráfico em
papel milimetrado, colocando a corrente no eixo das abscissas (eixo x) e a
tensão no eixo das ordenadas (eixo y).
2. Coloque os pontos referentes às incertezas somente da tensão elétrica: para
cada corrente haverá um valor de tensão mínima, o valor da tensão aplicada
pela fonte e um valor de tensão máxima, obtido pela respectiva subtração e
soma do valor da tensão aplicada com a amplitude da incerteza estimada.
3. Ajuste esses pontos por uma reta utilizando o Método dos Mínimos Quadrados
(vide anexo 4).
4. Obtenha o valor da resistência do resistor a partir do coeficiente angular da reta
ajustada pelo Método dos Mínimos Quadrados (vide anexo 4).
5. Calcule o coeficiente angular a partir dos pontos obtidos experimentalmente,
medição da corrente e tensão que será o valor da resistência medida
experimentalmente (vide anexo 4).
6. Compare os dois valores de resistência elétrica obtidos nos itens anteriores e
explique a diferença obtida entre os valores, uma vez que o resistor era um só.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
13
SP 04/05/14 (v9s)
Referências
1) http://rmeletronica.com.br/arquivos/resistor/6band.html
2) https://sites.google.com/site/mmprojetoseletronicos/estudos/codigo-de-cores-deresistores
3) http://educar.sc.usp.br/fisica/erro.html
4) https://sites.google.com/site/mmprojetoseletronicos/estudos/codigo-de-cores-deresistores/grafico01.bmp?attredirects=0
5) http://www.roteirosdefisica003.ufba.br/anexo04.pdf
6) http://www1.univap.br/rspessoa/aulas/fisicaexp2012/topico11fisicaexp.pdf\
7) Apostila do Laboratório de Física 1 - Elementos da Teoria dos Erros
Instituto de Física da Universidade de São Paulo, 1987
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
14
SP 04/05/14 (v9s)
Anexo 1 – Abordagem sobre resistores e seu código de cores
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
15
SP 04/05/14 (v9s)
Os resistores tem faixas coloridas para indicar o seu valor, existem resistores com 3 faixas, 4
faixas, 5 faixas e 6 faixas.
Quando um resistor tem 3 faixas é porque ele tem uma tolerância de ±20%.
Abaixo temos a Tabela 1 que informa o significado de cada faixa sendo:
Amarelo = valor significativo
Verde = quantia de zeros
Ciano = tolerância
Roxo = coeficiente de temperatura em PPM/°C. PPM/°C é a variação de tantas
partes por milhão a cada variação de grau Centigrado.
Resistores 3 Faixas
Resistores 4 Faixas
Resistores 5 Faixas
Resistores 6 Faixas
faixa 1 = significativo faixa 1 = significativo faixa 1 = significativo faixa 1 = significativo
faixa 2 = significativo faixa 2 = significativo faixa 2 = significativo faixa 2 = significativo
faixa 3 = quantia de faixa 3 = quantia de
zeros
zeros
Tolerância = ± 20% faixa 4 = tolerância
faixa 3 = significativo faixa 3 = significativo
faixa 4 = quantia de
zeros
faixa 5 = tolerância
faixa 4 = quantia de
zeros
faixa 5 = tolerância
faixa 6 = coeficiente de
temperatura em PPM/C
Tabela 1 – Significado das faixas coloridas
As cores das faixas significativas, quantia de zeros, tolerância e a ultima faixa que fornece a
variação da resistência em função da temperatura seguem o padrão de correspondências com
números. Vide Tabela 2 abaixo.
Tabela 2 – Codificação numérica das cores de resistores
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
16
SP 04/05/14 (v9s)
Entendendo a 6ª faixa, coeficiente de temperatura em PPM/°C.
COR
VALOR
BRANCO VIOLETA
1
5
AZUL
10
LARANJA AMARELO VERMELHO
15
25
50
OURO
100
Tabela 3 – Faixa do coeficiente de temperatura
A 6ª faixa só é utilizada em circuitos de muita precisão. A equação determina a resistência:
Rt = ( ( ( Tt – Ta ) . ( PPM / 1000000 ) ) . Ra ) + Ra
Sendo:
Rt = Valor da resistência na temperatura Tt
Ra = Valor da resistência na Ta
Ta = Temperatura ambiente
Tt = Temperatura de trabalho
PPM = Variação da resistência em partes por milhão à cada grau °C
Exemplo 1: Resistores de 3 faixas.
faixa 1 = marrom = 1 = 1 faixa 2 = preto = 0 = 0 faixa 3 = vermelho = 2 = 00
Valor lido
= 1000Ω = 1KΩ
Tolerância
= +-20% = 200Ω
O resistor pode ser de: 1000Ω - 200Ω -20% de tolerância
1000Ω + 200Ω +20% de tolerância
800 Ω < Resistência < 1200Ω
Exemplo 2: Resistores de 4 faixas.
faixa1 = amarelo = 4 = 4 faixa2 = violeta = 7 = 7 faixa3 = laranja = 3 = 000
Valor lido
= 47000Ω = 47KΩ
faixa4 Tolerância = ouro = +-5% = +-2350Ω
O resistor pode ser de: 47000Ω - 2350Ω -5% de tolerância
47000Ω + 2350Ω +5% de tolerância
44650Ω < Resistência < 49350Ω
Exemplo 3: Resistores de 5 faixas.
faixa1=verde=5=5 faixa2=azul=6=6 faixa3=cinza=8 =8 faixa4=vermelho=2=00
Valor lido
= 56800Ω = 56K8Ω
faixa5 Tolerância = marrom = +-1% = +-568Ω
O resistor pode ser de: 5680Ω - 568Ω -1% de tolerância
56800Ω + 568Ω +1% de tolerância
56232Ω < Resistência < 57368Ω
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
17
SP 04/05/14 (v9s)
Exemplo 4: Resistores de 6 faixas.
faixa=laranja=3=3 faixa2=laranja=3=3 faixa3 = branco=9=9 faixa4=preto=0=0 zeros
Valor lido
= 339Ω
faixa5 Tolerância = vermelho = +-2% = +-6,78Ω
O resistor pode ser de:
339Ω - 6,78Ω -2% de tolerância
339Ω + 6,78Ω +2% de tolerância
332,22Ω < Resistência < 345,78Ω
Agora a 6ª faixa, faixa6 amarelo=25PPM/oC
Este resistor foi medido em um ohmímetro de precisão na temperatura de 25 oC sendo o valor
lido de 339,2Ω. Então a sua resistência na temperatura de 42 oC
Aplicando-se a formula conhecida:
Rt = ( ( ( Tt – Ta ) . ( PPM / 1000000 ) ) . Ra ) + Ra
Rt = ( ( ( 42 – 25 ) . ( 25 / 1000000 ) ) . 339,2 ) + 339,2
Rt = 339,344Ω
Montando um gráfico para este resistor em função da tolerância e da PPM/oC mostrando 50oC
acima e a baixo da Ta: Por padrão a Ta "Temperatura ambiente" tem como valor 25oC. Na Ta
"25oC" o resistor pode ter qualquer valor entre 332,22Ω e 345,78Ω, pois sua tolerância é de
2%. A cada grau acima de 25oC a sua resistência sobe 0,0025% e a cada grau que desce
abaixo de 25C a sua resistência cai 0,0025%. este valor de porcentagem é o valor da PPM/C
dividido por 1000000 e em seguida multiplicado por 100.
Agora com os dois fatores será apresentado o Gráfico 01.
Gráfico 01 – Temperatura [°C] x Resistência Elétrica [Ω]
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
18
SP 04/05/14 (v9s)
Alem dos resistores convencionais abordados até o momento, podemos citar os resistores
SMD (superficial monting device) ou SMT (Surface Mount Tecnology) que foram
desenvolvidos principalmente visando a otimização de espaços, estes componentes podem
ser montados em ambos os de um placa de circuito impresso reduzindo sensivelmente os
espaços utilizados.
Resistor SMT (Surface Mount Tecnology)
1º Valor=1º número
2º Valor=2º número
3º Valor=Multiplicador
Neste exemplo a resistência tem um valor de:
1200 ohms = 1K2
1º Valor=1º número
O "R" indica virgula
3º Valor=2º número
Neste exemplo a resistência tem o valor de:
1,6 ohms
"R" indica " 0. "
2º Valor = 2º número
3ª Valor = 3º número
Neste exemplo a resistência tem o valor de:
0.22 ohms
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
19
SP 04/05/14 (v9s)
Anexo 2 - Arredondamento da numeração decimal
A norma técnica ABNT/NBR 5891/1977 (com código secundário ABNT/NB 87/1961)
dispõe sobre as regras de arredondamento da numeração decimal e mostra sua
aplicação.
Detalhadamente o que diz essa norma técnica:
Primeiramente, escolhe-se a casa decimal em que se quer fazer a aproximação e
depois aplicamos uma das seguintes regras:
Primeira regra: Quando o último algarismo a ser conservado for seguido de um
algarismo inferior a 5, o ultimo algarismo a ser conservado permanece sem
modificação. Exemplo: Arredondar o numero 26,63387 na segunda casa décima.:
1-Ultimo algarismo a
ser conservado.
3-O ultimo algarismo a ser conservado
permanece sem modificação.
26,63387 ≌ 26,63
2-Algarismo imediatamente
seguinte ao ultimo algarismo a
ser conservado é inferior a 5.
Segunda regra:
(a) Quando o algarismo imediatamente seguinte ao ultimo algarismo a
ser conservado for maior 5, o ultimo algarismo a ser conservado devera ser
aumentado de uma unidade
1-Ultimo algarismo a
ser conservado.
3-O ultimo algarismo a ser
conservado devera será
incrementado de uma unidade.
26,66800 ≌ 26,67
2-Algarismo imediatamente
seguinte ao ultimo algarismo a
ser conservado é maior que 5.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
20
SP 04/05/14 (v9s)
(b): Quando o algarismo imediatamente seguinte ao ultimo algarismo a ser
conservado for igual 5 e seguido de no mínimo um algarismo diferente de zero, o ultimo
algarismo a ser conservado devera ser aumentado de uma unidade.
.
1-Ultimo algarismo a
ser conservado.
4-O ultimo algarismo a ser conservado devera
será incrementado de uma unidade.
26,665008 ≌ 26,67
2-Algarismo imediatamente seguinte ao ultimo
algarismo a ser conservado é igual a 5.
3-Se após o algarismo 5 existir pelo menos
um algarismo diferente de 0.
Terceira regra Algarismo a ser conservado é impar: Quando o algarismo
imediatamente seguinte ao ultimo algarismo a ser conservado for maior 5 seguido de
zeros, deve-se arredondar o algarismo a ser conservado para o algarismo par mais
próximo.
1-Ultimo algarismo a ser conservado é
impar.
3-O ultimo algarismo a ser conservado
devera será o próximo algarismo par.
26, 675000 ≌ 26,68
2-Algarismo imediatamente seguinte ao
ultimo algarismo a ser conservado é 5.
Quarta regra Algarismo a ser conservado é par: Algarismo a ser conservado é
par. Quando o algarismo imediatamente seguinte ao ultimo algarismo a ser conservado
for maior 5 seguido de zeros, o algarismo a ser conservado permanece sem
modificação.
1-Ultimo algarismo a ser
conservado, algarismo é par.
3-O ultimo algarismo a ser conservado
permanece sem modificação.
26, 665000 ≌ 26,66
2-Algarismo imediatamente seguinte ao ultimo
algarismo a ser conservado é 5 seguido de
zeros.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
21
SP 04/05/14 (v9s)
Anexo 3 – Introdução a Teoria dos Erros
O que é a Teoria dos Erros
Uma vez que medimos uma grandeza física, encontrando um número que o
caracterize, necessitamos saber com que confiança esse valor representa mesmo a
grandeza física a qual estamos nos referindo quando aplicamos esse resultado, por
exemplo, quando medimos a corrente elétrica que circula num aparelho eletrônico,
necessitamos saber o quanto esse valor está próximo do real para podermos
dimensionar adequadamente uma proteção (um fusível) para ele.
Sabemos que toda medida carrega uma incerteza, então, devemos expressá-la de uma
maneira compreensível a todas as pessoas que irão utilizar esse valor medido através
do uso de uma linguagem universal, além de se utilizar métodos adequados para
combinar essas diversas incertezas.
O tratamento que damos a uma medida para mostrar o grau de confiança desse valor
para aplicação expresso numa linguagem universal, utilizando-se métodos de avaliação
das incertezas compõem o que chamamos de Teoria dos Erros.
O que é medida
As grandezas físicas são determinadas por medidas ou combinações de medidas;
estas medidas representam, então, as dimensões das grandezas físicas.
Algarismos significativos
Em medições de grandezas físicas, costuma-se fazer estimativas com aproximações
de frações da menor divisão da escala do instrumento.
Pode-se fazer aproximações de até décimos da menor divisão da escala, contudo,
estimar-se centésimos ou milésimos está fora dos limites de percepção da maioria dos
seres humanos.
Na régua abaixo, temos 1 mm como a menor divisão da escala, então, quando
realizamos uma medida com a régua milimetrada (figura abaixo) da dimensão da
largura S do retângulo, obtemos
S = 40,3 mm
Esta medida apresenta três dígitos ou três algarismos dos quais o dígito ou algarismo 3
resultou da fração avaliada da menor divisão da escala do instrumento, por isso, nele
reside a dúvida ou incerteza da medida realizada.
Os dois primeiros dígitos, 4 e 0, constituindo o número 40, são isentos de dúvidas (se
outros operadores do instrumento de medida medissem a largura S, obteriam valores
divergentes apenas no algarismo 3 e nunca no 4 e 0).
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
22
SP 04/05/14 (v9s)
Consideramos algarismos significativos de uma medida os algarismos corretos mais o
primeiro duvidoso.
2 algarismos corretos
S = 40,3 mm
1 algarismo duvidoso
No exemplo acima, a medida S tem três algarismos significativos:
Quantidade algarismos
significativos
=
Quantidade algarismos
corretos
+
Um algarismo duvidoso
(primeiro)
Operações com algarismos significativos
Há regras para operar com algarismos significativos. Se estas regras não forem
obedecidas, podemos obter resultados que podem conter algarismos que não são
significativos.
a) Adição e subtração
Vamos supor a seguinte operação de adição:
250,657 + 0,0648 + 53,6 =
Para isto observamos qual a parcela que apresenta o menor número de algarismos
significativos. No caso 53,6 que apresenta apenas uma casa decimal. Esta parcela
será mantida e as demais serão aproximadas para uma casa decimal observando as
regras de arredondamento (anexo 2).
Então:
250,657 ≌ 250,7
0,0648 ≌ 0,1
Daí:
250,7 + 0,1 + 53,6 = 304,4 cm
Na subtração, o procedimento é o mesmo.
b) Multiplicação e divisão
Multiplicando 6,78 por 3,5 obtemos:
6,78 x 3,5 = 23,73
Temos no resultado deste produto algarismos que não são significativos.
A seguinte regra é adotada: Verificar qual o fator que apresenta o menor número de
algarismos significativos e apresentar no resultado apenas a quantidade de algarismo
igual a deste fator, observando as regras de arredondamento.
6,78 x 3,5 = 23,7
Para a divisão o procedimento é análogo.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
23
SP 04/05/14 (v9s)
Observação: As regras para operar com algarismos significativos não são rígidas.
Poderia ser mantido perfeitamente um algarismo a mais no produto. Os dois resultados
são aceitáveis:
6,78 x 3,5 = 23,73 ou 6,78 x 3,5 = 23,7.
O que é incerteza de uma medida
Como as medidas são obtidas a partir da utilização de aparelhos de medição por
pessoas que fazem estas medições, as medidas têm uma incerteza intrínseca
proveniente das características desses aparelhos e também devido ao próprio
operador.
Mesmo que uma mesma medida seja repetida várias vezes com a mesma precaução
por um observador ou vários, os resultados nunca serão os mesmos.
Assim, toda medida de uma grandeza física carrega uma incerteza em seu valor.
Em termos práticos, a incerteza é a fração avaliada da menor divisão da escala, isto é,
ao medirmos uma grandeza, no dígito duvidoso é que reside a incerteza dessa medida,
por exemplo, ao medirmos um comprimento AB, obtemos
AB = 12, 6 cm
este dígito apresenta uma incerteza
Isto significa que a medida AB pode ser:
12,7 cm ou 12,5 cm, ou ainda,
12,8 cm ou 12,4 cm.
O operador deve fixar a amplitude da incerteza, expressando-a da seguinte forma:
AB = (12,6 ± 0,1) cm ou
AB = (12,6 ± 0,2) cm no segundo caso
Tipos de incerteza
Incerteza absoluta é a amplitude de incertezas fixada pelo operador, expressa por m =
(12,6 ± 0,2) kg.
Incerteza relativa é igual ao quociente entre a incerteza absoluta e a medida da
grandeza, expressa em porcentagem m = 1,6 %.
Assim, quanto menor a incerteza relativa, maior a qualidade da medida.
Flutuações das medidas (erros)
O objetivo de uma medida é alcançar o valor real da grandeza física, o que é
impossível, contudo, podemos alcançar um valor que mais se aproxima do valor real.
A essa diferença entre o valor real (valor verdadeiro) e o valor medido da grandeza
física damos o nome de ERRO.
Os erros que acompanham as medidas são a causa de não se conseguir obter o valor
verdadeiro de uma grandeza física e podem ser de origem sistemático ou acidental
(aleatório).
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
24
SP 04/05/14 (v9s)
Erro sistemático
Os erros sistemáticos são originados pelas falhas do método empregado ou defeito do
operador, por exemplo:
a) Calibração errônea de uma régua ou escala de instrumento
b) Relógio descalibrado que sempre atrasa ou sempre adianta
c) Influência do potencial de contato numa medida de tensão
d) Tempo de resposta de um operador que sempre se adianta ou sempre se atrasa
nas observações
e) Operador que sempre subestima ou sempre superestima os valores das
medidas
Pela natureza desse tipo de erro, os erros sistemáticos provocam uma incerteza de
amplitude regular e influenciam nas medidas sempre num mesmo sentido, ou para
mais ou para menos. Por exemplo, devido à dilatação, uma medida numa régua nunca
corresponderá ao valor real e as medidas tomas com essa régua sempre serão sujeitas
a erros sistemáticos que influenciarão no resultado sempre num mesmo sentido e
sempre com a mesma amplitude.
Erro acidental (ou aleatório)
Os erros acidentais ou aleatórios são aqueles cujas causas são fortuitas, acidentais e
variáveis. Suas amplitudes estão compreendidas dentro da aproximação dos
instrumentos de medição e variam conforme a tomada da medida pelo operador, por
exemplo:
Imperícia do operador
a) Variação na capacidade de avaliação ( número de medidas efetuadas, cansaço,
etc)
b) Erro de paralaxe na leitura de uma escala
c) Reflexos variáveis do operador (pressionar o botão de acionamento de um
cronômetro)
Assim, os erros acidentais ou aleatórios podem acontecer em diversas amplitudes e
sentidos, tanto para mais como para menos, podendo ser minimizados pela perícia do
operador, mas jamais eliminados por completo.
Propagação de Erros
Muitas grandezas físicas são determinadas indiretamente por operações algébricas
entre medidas.
Por exemplo, a velocidade média de um veículo é obtida medindo-se o percurso feito
por ele (deslocamento ∆) e tempo gasto (∆para perfazer este percurso, sendo
∆
∆
Se as medidas das grandezas ∆∆ são afetadas por erros, ocasionando uma
incerteza das medidas, na divisão ∆/∆ estes erros se combinarão, afetando o valor
de vm.
Tem-se, então, uma propagação de erros.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
25
SP 04/05/14 (v9s)
, , , . . , Se uma grandeza V é função de outras grandezas (variáveis a, b, c, ..., k)
a incerteza de V é dado por:
" $ $
" $ $
" $ $
" $ $
! # . % ! # . & ! # . ' ⋯ ! # . ( )
"
"
"
"
*+
$
onde:
- $
, . é a derivada parcial da função V(a,b,c,...,k) em relação ao parâmetro a.
-%
- $
, . é a derivada parcial da função V(a,b,c,...,k) em relação ao parâmetro b.
-&
- $
, . é a derivada parcial da função V(a,b,c,...,k) em relação ao parâmetro c.
-'
- $
, . é a derivada parcial da função V(a,b,c,...,k) em relação ao parâmetro k.
-(
sa , sb , sc e sc são as incertezas de a, b, c, ..., k respectivamente,
a) Incerteza da Soma ou Diferença
Seja uma grandeza dada pela soma ou subtração de outras duas:
As incertezas das medidas a e b são, respectivamente, sa , sb
absoluta de V, será:
e sV, a incerteza
/%$ &$ b) Produto
Seja uma grandeza dada pelo produto de outras três:
As derivadas parciais são:
-
-
-%
-&
-
-'
As incertezas das medidas a, b e c são, respectivamente, sa , sb e sc .
A incerteza absoluta de V será:
/ $ $ %$ $ $ &$ $ $ '$ Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
26
SP 04/05/14 (v9s)
A incerteza relativa de V será:
%$ &$ '$
01 $ $ $ 2
c) Quociente
Seja uma grandeza dada pelo divisão entre outras duas:
As derivadas parciais são:
-
*
-
3%
4
-%
&
-&
&
As incertezas das medidas a, b e c são, respectivamente, sa e sb .
A incerteza absoluta de V será:
A incerteza relativa de V será:
d) Caso Geral
As derivadas parciais são:
-
9 63* 7 8
-%
%$ $ $
0 $ 5 &
%$ &$
01 $ $ 2
6 7 8
etc
As incertezas das medidas a, b e c são, respectivamente, sa , sb e sc .
A incerteza relativa de V será:
9 $ . %
: $ . &
; $ . '
0
$
$
$
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
$
$
$
27
SP 04/05/14 (v9s)
Anexo 4 – Ajuste de Retas por Mínimos Quadrados
Se um certo número de medidas é tomado de uma mesma grandeza física e se estas
medidas estão sujeitas a erros aleatórios apenas, então, a Teoria dos Mínimos
Quadrados estabelece que o valor mais provável da quantidade medida é aquele que
faz a soma dos quadrados dos erros ser mínima.
Ao se obter uma sucessão de medidas experimentais que, representados em um
gráfico apresentam comportamento linear, diferentes pessoas poderão traçar diferentes
retas, encontrando diferentes valores para os coeficientes linear e/ou angular.
O método dos mínimos quadrados permite determinar qual a reta correta, ou seja, a
que mais se ajusta às medidas obtidas, consistindo em determinar o coeficiente
angular a e o coeficiente linear b da equação da reta: y = ax + b.
O ajuste de curvas pelo método dos mínimos quadrados é importante, pois ao contrário
do método gráfico, é independente da avaliação do experimentador.
Este método consiste em minimizar o erro quadrático médio (S) das medidas.
Considere um conjunto de N medidas (xi, yi), com i assumindo valores inteiros desde 1
até N, S é definido como:
@
@
?A*
?A*
< = Δ<? =: B :? $
na qual, y é o valor da curva ajustada (y = ax + b).
O objetivo é somar os Δ<? das N medidas e traçar uma reta que torne a soma dos Δ<?
mínima.
-C
-C
Matematicamente, isto corresponde a zerar as derivadas parciais -% 0 e -& 0.
É razoável acreditar que para isso aconteça a reta desejada deve passar entre todos
os pontos experimentais.
Destas derivadas parciais calculamos os valores dos parâmetros a e b, obtendo:
ou seja,
@
@
E ∑@
?A* 9? :? B ∑?A* 9? ∑?A* :?
$
@
$
E ∑@
?A* 9? B ∑?A* 9? GE. HIJ9:K B GHIJHLHMJ9. HIJHLHMJ:K
GE. HIJ9 $K B HIJHLHMJ9$
GHIJ9 $ . HIJHLHMJ:K B GHIJ9:. HIJHLHMJ9K
GE. HIJ9 $K B HIJHLHMJ9$
Na prática, elaboramos tabelas com os vários valores das medidas de x, y e dos
resultados de xy e x2, fazendo a somatória ao final da coluna. Com os valores dos
resultados das somas, substituímos nas fórmulas acima e obtemos os valores dos
coeficientes a e b da reta ajustada.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
28
SP 04/05/14 (v9s)
Exemplo prático de determinação dos coeficientes angulares e lineares de uma
reta utilizando o Método dos Mínimos Quadrados
Considere uma medida de movimento retilíneo uniforme (MRU) efetuado por um
carrinho no laboratório. Foram medidos tanto sua posição (em metros) quanto o tempo
(em segundos) e os resultados colocados na tabela 1, observando que os valores do
tempo serão colocados no eixo das abscissas (eixo x – horizontal) e os valores da
posição serão colocados no eixo das ordenadas (eixo y – vertical).
Tabela 1 – Valores experimentais da posição de um carrinho em função do tempo.
Tempo (segundos)
0,100
0,200
0,300
0,400
0,500
Posição (metros)
0,51
0,59
0,72
0,80
0,92
Para usarmos o Método dos Mínimos Quadrados, devemos construir uma tabela com
os valores de x, y, xy e x2, com as respectivas somas ao final de cada coluna, conforme
indicado a seguir, lembrando que aqui o eixo x corresponde ao tempo t e o eixo y à
posição x:
Tabela 2 – Valores de x, y, x.y e x2, e suas respectivas somatórias.
Tempo - x (s)
0,100
0,200
0,300
0,400
0,500
= N , OP
Posição - y (m)
0,51
0,59
0,72
0,80
0,92
= Q , OR
x.y
0,051
0,120
0,220
0,320
0,460
= NQ , S
x2
0,0100
0,0400
0,0900
0,1600
0,2500
= N P, OO
Com esses resultados, substituir os valores nas fórmulas para os coeficientes a e b,
considerando que neste caso N = 5 medidas:
591,17 B 1,5093,54 5,85 B 5,31 0,54
1,08
590,55 B 1,50$
2,75 B 2,25 0,50
0,5593,54 B 1,1791,50 1,95 B 1,76 0,19
0,38
590,55 B 1,50$
2,75 B 2,25 0,50
Portanto, a equação da reta ajusta pelo Método dos Mínimos Quadrados será:
: 1,089 0,38
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
29
SP 04/05/14 (v9s)
E a nova tabela com os valores estimados da posição do carrinho a partir do Método
dos Mínimos Quadrados será:
Tabela 3 – Valores da posição estimados a partir do Método dos Mínimos Quadrados.
Tempo (segundos)
0,100
0,200
0,300
0,400
0,500
Posição Estimada (metros)
Método dos Mínimos Quadrados
0,49
0,60
0,70
0,81
0,92
O gráfico a seguir mostra os resultados da tabela 1 com os valores medidos da posição
e os da tabela 3 com os valores da posição do carrinho usando o Método dos Mínimos
Quadrados:
O valor da velocidade média calculado pelos dados da tabela 1 é igual a 0,97 m/s:
A
Δ9 M]çãHJ`H]çãH
0,80 B 0,51
0,29
0,97I/
Δ
]aMLHJI`H 0,400 B 0,100 0,30
enquanto que para a curva determinada pelo Método dos Mínimos Quadrados é de
1,08 m/s (coeficiente a da equação da reta ajustada), ou seja, este é o valor mais
próximo do valor real da velocidade do carrinho.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
30
SP 04/05/14 (v9s)
Anexo 5 – Utilização dos Instrumentos
1- Multímetros
O multímetro, também conhecido como VOM (Volt-Ohm-Miliamperímetro), Ohmimetro,
Multiteste ou Tester é um instrumento destinado a medida de grandezas elétricas. Em
eletricidade existem três grandezas básicas (tensão, corrente e resistência elétrica) que
o multiteste ou multímetro mede com precisão e, baseados nelas, podemos empregar
este instrumento numa infinidade de aplicações. Atualmente o tipo mais comum é
mostrado nas figuras abaixo.
Disponibilidade no laboratório:
Multímetros Minipa ET-3200 – alicate amperímetro em uso no laboratório: este
instrumento não realiza medições de Corrente Continua.
Em qualquer instrumento
de medição:
Sempre selecione o maior
valor de escala da
grandeza que desejamos
medir e depois diminua a
escala, até adequar o valor
lido no display ao valor
real.
Selecione uma das posições desta área para
medir uma determinada corrente alternada
que circula em um condutor, nestas posições
somente o alicate estar habilitado a realizar
medições.
Selecione uma das posições
desta área para medir uma
determinada Tensão
Alternada em um
determinado ponto de um
circuito.
Utilizar as pontas de prova
para estas medidas.
Selecione uma das
posições desta área para
medir uma determinada
Resistência. Utilizar as
pontas de prova para estas
medidas.
Para realização de
medidas das grandezas
Tensão CC, Tensão CA, e
Resistência as pontas de
prova deverão estar
colocadas na posição
abaixo
Selecione uma das posições
desta área para medir uma
determinada Tensão Continua
em um determinado ponto de
um circuito.
Utilizar as pontas de prova
para estas medidas.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
31
SP 04/05/14 (v9s)
Multímetros Minipa ET-1002 – Multímetro Digital em uso no laboratório: este
instrumento não realiza medições de Corrente Alternada.
Em qualquer instrumento
de medição:
Sempre selecione o maior
valor de escala da
grandeza que desejamos
medir e depois diminua a
escala, até adequar o
valor lido no display ao
valor real.
Selecione uma das posições desta área
para medir uma determinada Tensão
Alternada em um determinado ponto de
um circuito.
Utilizar as pontas de prova para estas
medidas.
Selecione uma das posições desta área para
medir uma determinada Tensão Continua
em um determinado ponto de um circuito.
Utilizar as pontas de prova para estas
medidas.
Selecione esta posição
para fazer a avaliação de
Transistores. Utilizar as
pontas de prova para
estas medidas
Selecione uma das posições desta área para
medir uma determinada corrente continua
que circula em um circuito. Para correntes
de ate 200 mA a posição das pontas de
provas á a mesma da mostrada ao lado e
abaixo. Quando a corrente for maior que 200
mA devemos mudar a ponta de prova
vermelha para a posição abaixo e selecionar
a posição 10A. Utilizar as pontas de prova
para estas medidas.
Selecione uma das
posições desta área para
medir uma determinada
Resistência. Utilizar as
pontas de prova para
estas medidas.
Para realização de medidas
das grandezas Tensão CC,
Tensão CA, e Resistência
as pontas de prova deverão
estar colocadas na posição
abaixo
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
Selecione esta posição
para fazer a avaliação de
diodos. Utilizar as pontas
de prova para estas
medidas
32
SP 04/05/14 (v9s)
Multímetros Minipa ET-2042D – Multímetro Digital em uso no laboratório: o modelo
mais completo disponível no laboratório. Mensura Corrente Continua e corrente
Alternada ate 20A.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
33
SP 04/05/14 (v9s)
Selecione uma das posições desta
área para medir uma determinada
Resistência. Utilizar as pontas de
prova para estas medidas.
Selecione esta
posição para fazer a
avaliação de diodos.
Utilizar as pontas de
prova para estas
medidas.
Em qualquer instrumento de medição:
Sempre selecione o maior valor de
escala da grandeza que desejamos
medir e depois diminua a escala, até
adequar o valor lido no display ao valor
real.
Com este procedimento evitamos
qualquer dano ao equipamento.
Congela a
informação
no display
Liga e desliga
Back Light do
display.
Selecione uma das posições
desta área para medir uma
determinada Tensão
Continua em um determinado
ponto de um circuito.
Utilizar as pontas de prova
para estas medidas.
Selecione uma das
posições desta área
para medir uma
determinada Tensão
Alternada em um
determinado ponto de
um circuito.
Utilizar as pontas de
prova para estas
medidas.
Selecione esta posição
para fazer a avaliação de
frequência de 2Khz a
200Khz. Utilizar as pontas
de prova para estas
medidas.
Selecione esta posição para
fazer a avaliação do hFe de
Transistores. Utilizar as pontas
de prova para estas medidas.
Para realização de medidas
das grandezas Tensão CC,
Tensão CA, e Resistência as
pontas de prova deverão estar
colocadas na posição abaixo
Selecione esta
posição para fazer a
avaliação da
capacitância de
capacitores. Utilizar
as pontas de prova
para estas medidas.
Selecione esta
posição para
fazer a avaliação
da Temperatura.
Utilizar as
pontas de prova
especial que
acompanham o
equipamento.
Selecione uma das posições desta área
para medir uma determinada corrente
continua que circula em um circuito.
Para correntes de ate 200 mA a
posição das pontas de provas devem
ser a mostrada abaixo. Quando a
corrente for maior que 200 mA
devemos mudar a ponta de prova
vermelha para a posição abaixo e
selecionar a posição 20A. Utilizar as
pontas de prova para estas medidas.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
Selecione uma das posições desta área para
medir uma determinada corrente alternada que
circula em um circuito. Para correntes de ate 200
mA a posição das pontas de provas devem ser a
mostrada abaixo. Quando a corrente for maior
que 200 mA devemos mudar a ponta de prova
vermelha para a posição abaixo e selecionar a
posição 20A. Utilizar as pontas de prova para
estas medidas.
34
SP 04/05/14 (v9s)
Ligação do Multímetro
Amperímetro
O amperímetro é um instrumento utilizado para fazer a medida da intensidade no fluxo
da corrente eletrica que passa através da sessão transversal de um condutor. A
unidade de medida usada é o Ampère.
Quando utilizamos o multimetro na escala Corrente Alternada ou Continua, este se
comporta como um amperimeto, nos dando o valor da corrente que esta circulando no
condutor neste trecho do circuito.
O simbolo utiizado para indicar o uso de um amprerimeto segue abaixo:
Nunca esqueça o amperímetro possui uma resistência
interna muitíssimo BAIXA e sempre deve ser ligado em
SÉRIE com o condutor no qual desejamos mensurar a
CORRENTE que por ele circula.
Voltimetro
O voltimetro é um instrumento utilizado para fazer a medida do valor da tensao que
esta sendo aplicada em um determinado ponto de um circuito. A unidade de medida
usada é o Volt.
Quando utilizamos o multimetro na escala Tensão Alternada ou Continua, este se
comporta como um voltimetro, nos dando o valor da tensão aplicada no ponto no qual
ele é colocado.
O simbolo utiizado para indicar o uso de um voltimetro segue abaixo:
Nunca esqueça o voltímetro possui uma resistência interna
muitíssimo ALTA e sempre deve ser ligado em PARALELO
no ponto que desejamos mensurar a TENSÃO.
Ohmimetro
O Ohmímetro é um instrumento de medida eletrica que mede a resistencia eletrica. Ou
seja a oposição a passagem de corrente elétrica. O ohmímetro e provido de uma
bateria interna que aplica uma tensão a resistência, e atravez da primeira lei de Ohm
calcula o valor da resistencia.
Quando utilizamos o multimetro na escala Resistencia, este se comporta como um
ohmímetro, nos dando o valor da resistencia que esta sendo mensurada.
O simbolo utiizado para indicar o uso de um ohmímetro segue abaixo:
Nunca esqueça o ohmímetro NUNCA deve ser utilizado com
o circuito alimentado. Para medirmos o valor de uma
resistência devemos retira-la do circuito.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
35
SP 04/05/14 (v9s)
2- Proto-Boards
Também conhecida como MATRIZ DE CONTATO. A proto-board consiste de uma
placa de alumínio sobre a qual são presos conjuntos de estruturas plásticas vazadas. A
proto board apresenta abaixo dos quadrados de plástico, uma série de duas lâminas
folheadas a ouro ou cobre, entre as quais os fios ou os componentes serão
conectados, estabelecendo um contato elétrico, aceita somente projetos de baixa
potência (2 - 3A).
Aspectos Construtivos da
protoboard
Placa de circuito onde são
definidas as trilhas que por
sua vez definem as ligações
disponíveis na protoboard.
Desenho de placa para ser
produzida
em
circuito
impresso.
Outra possibilidade, a
disponibilizada no laboratório,
o mesmo circuito da placa ao
lado (esquerdo) agora não
mais produzida em circuito
impresso, mas sim, são
colocados lado a lado
diversos contatos metálicos
que funcionam como
presilhas, onde são inseridos
os terminais rígidos dos
componentes.
Colocação de uma Mascara de
plástico sobre os contatos metálicos.
Os contatos metálicos estão em
diferentes sentidos na matriz. Como
podemos observar nas figuras, a placa
de montagem possui a matriz principal
em seu meio, os contatos estão na
horizontal, marcados em azul sendo as
linhas eletricamente isoladas
Nestas indicações os contatos estão na
vertical.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
Utilização da
Protoboard
Por se tratar de uma
equipamento sem
resistência mecânica
NUNCA force a introdução
dos terminais dos
componentes no conector,
pois causará danos
irreparáveis a Protoboard.
36
SP 04/05/14 (v9s)
3- Fonte de alimentação.
Procedimento que devemos tomar como padrão não só no caso das fontes, mas
também na ligação de qualquer equipamento. Sempre que utilizarmos um
equipamento pela primeira vez devemos observar as características do
equipamento, evitando assim a ligação de equipamentos em alimentação que
não seja a compatível. Exemplo ligar um equipamento 110 V em alimentação
220V, ou ligar um componente de 3.2 Vcc em 5.0 Vcc, isto causara sérios danos
ao equipamento. Em nosso caso a Laboratorista já providenciou a ligação
adequada dos equipamentos, podendo este passo ser pulado.
SEMPRE verifique
com muita atenção
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
SEMPRE verifique
com muita atenção
37
SP 04/05/14 (v9s)
Fonte de Alimentação
Nos laboratórios temos a disponibilidade de dois modelos de fontes de Corrente
Continua. Ambos os modelos fornecem Corrente Continua com a tensão podendo ser
regulada de 0 a 30 Vcc com capacidade de suprir ate 3A. Estas fontes possuem dois
canais independentes, isto e podemos alimentar dois circuitos simultaneamente.
Fonte Digital 30V/3A Dupla=5V/3A Minipa MPC-303D, em uso no laboratório:
Chave de seleção.
Seleciona a
informação a ser
mostrada no
display Tensão ou
Corrente.
Led indicador
de qual
informação
esta sendo
mostrada no
display
Display indicador que mostra a tensão que esta
sendo aplicada em sua saída ou a corrente que
esta sendo fornecida ao circuito. Depende da
chave de seleção estar posicionada em tensão
VOLTS ou AMPS.
Todos os
controles
disponíveis para
o canal 1. De
maneira análoga
estão disponíveis
para o Canal 2.
Knobs de
regulagem de
saída de corrente.
Led indicador de
corrente de curto
circuito.
Botão
Liga/Desliga.
Saída de tensão regulada. Podendo variar
de 0 a 30 V. Esta é a posição dos cabos
que alimentarão os circuitos projetados
em protoboards.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
Led indicador que
a chave de
seleção esta para
tensão.
Knobs de
regulagem de
saída de tensão.
38
SP 04/05/14 (v9s)
Fonte Digital 30V/3A Dupla=5V/3A, Minipa MPL-3003D, em uso no laboratório.
Principal diferença com a fonte Minipa MPC-303D é a presença de dois displays para
cada canal de saída da fonte, um indicador de tensão e outro indicador de corrente.
Display indicador que
mostra a corrente que
esta sendo fornecida
ao circuito.
Todos os
controles
disponíveis para
o canal 1. De
maneira análoga
estão disponíveis
para o Canal 2.
Led indicador de
corrente de curto
circuito.
Knobs de
regulagem da
sensibilidade da
saída de corrente.
Led indicador de como
estão operando os dos
dois canais do
equipamento.
serie/paralelo/indepen
dente
Botão
Liga/Desliga.
Saída de tensão regulada. Podendo variar
de 0 a 30 V. Esta é a posição dos cabos
que alimentarão os circuitos projetados
em protoboards.
Knobs de
regulagem de
saída de
tensão.
Fontes variáveis simples e duplo canal com dissipação de calor.
Possui saída de tensão no formato USB.
• Saída Variável: Dupla
• Tensão/Corrente Variável: 0~30V/0~3A
• Saída Fixa: 5V/3A
• Possui Proteção de Sobrecarga
• Operação Tracking: Série / Paralelo
• Display: 3 Dígitos Quádruplo
• Precisão Básica do Display: 1%
• Regulação de Carga em Tensão: 0,1mV+5mV
• Regulação de Linha em Tensão: 0,1mV+3mV
• Regulação de Carga em Corrente: 2mV+5mA
• Regulação de Linha em Corrente: 2mA+3mA
• Ripple & Ruído (Tensão/Corrente): 0,5mV/3mA RMS
• Precisão de Saída Fixa: ±2,5%
• Método de Resfriamento: Dissipação de Calor
• Alimentação USB: 5V/1A
• Alimentação: 110/220V AC
• Dimensões(mm): 265x155x295
• Garantia: 12 meses
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
Display indicador que
mostra a tensão que
esta sendo fornecida
em sua saída
Seletor do tipo de ligação
dos dois canais. Fonte
dispõem do recurso de
ligarmos os dois canais em
serie/paralelo/independente.
Com isto podendo aumentar
a tensão/corrente de saída
dependendo do tipo de
ligação dos canais.
Normalmente operamos
com o seletor posicionado
em 2 fontes independentes.
39
SP 04/05/14 (v9s)
4- Conectando a Fonte a Protoboard
Como podemos observar na imagem abaixo, disponibilizamos dois tipos de cabos
para conexão da fonte a protoboard, convencionado que a alimentação positiva
esta sempre em fios vermelho ou laranja e a negativa em fios pretos ou verde.
Cabo de alimentação com terminal
“jacaré”, que devera estar conectado a
um fio que por sua vez estará conectado
no alojamento da protoboard.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
Cabo de alimentação com terminal
“banana”, ao qual foi conectado um fio
que por sua vez estará conectado no
alojamento da protoboard.
40
SP 04/05/14 (v9s)
5- Resistores e Fios para Conexão
Disponibilidade de diversos valore
de reitores no laboratório.
Podendo ser requisitados junto a
laboratorista quando necessário.
Resistores separados
aleatoriamente.
Cabo de rede CAT 5e, solido, par
trançado sem a cobertura de
proteção azul.
Prof. José dos Santos Garcia Neto
Profa Suely Midori Aoki
Resistores separados
previamente escolhidos para
realização de experimentos.
Fios CAT 5e previamente
cortados e conformados para
utilização em conexão durante a
montagem de circuitos na
protoboard.
41
SP 04/05/14 (v9s)