Document

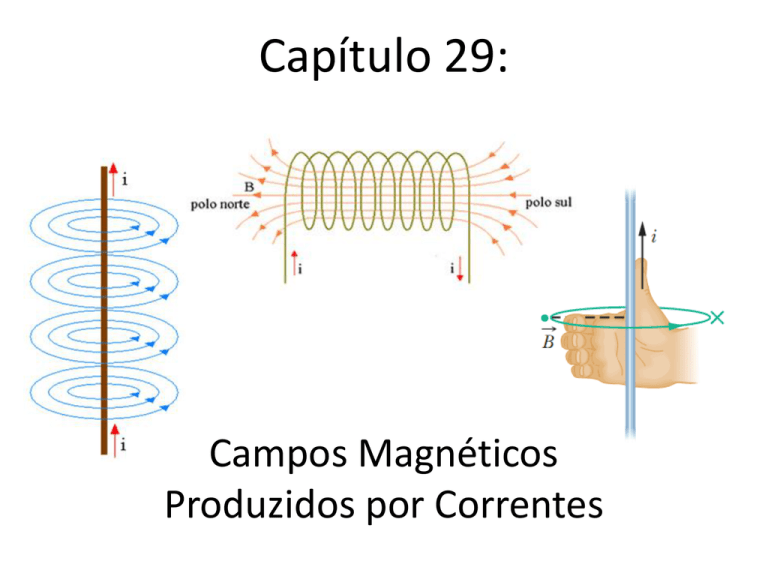
Capítulo 29:
Campos Magnéticos
Produzidos por Correntes
Cap. 29: Campos Magnéticos
Produzidos por Correntes
Índice
 Lei de Biot-Savart;
 Cálculo do Campo Produzido por uma Corrente;
 Força Entre duas Correntes Paralelas;
 Lei de Ampère;
 Solenóides e Toróides;
 Uma Bobina percorrida por Corrente como um Dipolo
Magnético.
Cap. 29: Geração de B por i
A Lei de Biot-Savart
Cargas em movimento geram Campo Magnético
 0 ids  r̂
dB 
4 r 2
 0 dq v  r̂
dB 
4 r 2
Lei de Biot-Savart
 0 =
T.m/A;
 O vetor r aponta do elemento de corrente em direção ao ponto onde o campo deve
ser determinado;
 O vetor ds é um infinitesimal de comprimento orientado na direção da corrente.
4x10-7
Ilustração das variáveis da Lei de Biot-Savart e da regra da mão direita, usada para determinar a
direção e o sentido do campo magnético gerado por uma corrente elétrica
Cap. 29: Geração de B por i
Fio Percorrido por uma Corrente
 0 ids  r̂
0 ids sen( )
dB 
dB 
2
4 r
4
r2

B 0
4


0i ds sen( )
ids sen( )

2
 r 2
4 0
r2
tg 
R
sen 
r
cos   
s
r
R
s
 1 
ds  R
d
2 
 sen  
0i 180 sen
0i 180
1
B
R
d 
send
2
2


4 0 (R/sen ) sen 
4R 0
 0i
180
B
( cos  ) 0
4R
 0i
B
2R
Campo Magnético de um
fio infinito
 0i
B
4R
Campo Magnético de meio
fio infinito em x = 0 (x = 0 até )
Cap. 29: Geração de B por i
Fio Percorrido por uma Corrente
 0 ids  r̂
0 ids sen( )
dB 
dB 
2
4 r
4
r2
 0i
B
2R
Campo Magnético de um
fio infinito
Cap. 29: Geração de B por i
Corrente em um Arco de Circunferência
0 ids sen( )
dB 
4
r2
 O ângulo  entre ds e r é sempre 90°
 r é constante (r = R).
ds  rd
f
B
0i( sen90)
 0i
Rd


( f  i )
2

4R
4R

i
 Para uma volta completa ( varia de 2
até 0).
B
 0i
2R
Campo Magnético gerado
Por uma espira.
Cap. 29: Geração de B por i
Corrente em um Arco de Circunferência
Exemplo 29-1) pg. 238
A figura abaixo mostra um fio percorrido por uma corrente i. Dois segmentos
retilíneos assim como um arco de circunferência com ângulo central de /2 rad
compõe a forma do fio. Determine o campo magnético no ponto C.
 O campo gerado no ponto C será
composto por 3 contribuições.
   
B  B1  B2  B3
0 ids sen( )
dB 
4
r2
 O campo gerado pelos segmentos
retilíneos 1 e 2 é nulo pois o ângulo  entre
a corrente e o vetor r é 0°.
 O campo gerado pelo arco de
circunferência constitui 1/4 do valor do
campo de uma espira.
 
B1  B2  0
1  0i
B  B3 
4 2R
B
 0i
8R
Cap. 29: Geração de B por i
Exemplo 29-2) pg. 239
A figura ao lado mostra dois fios longos percorridos por correntes i1 e i2. Determine o
módulo do campo magnético total no ponto P, para i1 = 15 A, i2 = 32 A e d = 5,3 cm.
 O campo gerado no ponto P será
composto por 2 contribuições.
  
B  B1  B2
 0i
B
2R
 Como o ângulo entre B1 e B2 é 90°,
temos:
B  B1  B2
2
 O campo de cada fio será:
B1 
 0i1
2dcos45
 8 10 5 T
2
B  1,89 104 T
B2 
 0i2
2dcos45
 1,708 10  4 T
  arctg
B1
 25
B2
Cap. 29: Geração de B por i
Forças Geradas por Correntes Paralelas
 Dois fios paralelos percorridos por correntes
ia e ib, sentem a ação de uma força.
 O campo gerado sobre o fio b pela corrente
ia.
0ia
Ba 
2d
 Para um elemento dl do fio b, temos:
 

dF  ib dl  Ba
0 Liaib
Fba 
2d
Fba  ib LBa sen90
 Correntes paralelas se atraem e correntes
antiparalelas se repelem.
Cap. 29: Geração de B por i
Forças Geradas por Correntes Paralelas
 Exemplo de aplicação da força gerada por correntes
paralelas: O Canhão Eletromagnético.
 Uma corrente elétrica
vaporização de um fusível.
elevada
provoca
a
 A corrente nos trilhos gera um campo magnético
que faz com que os gás (fusível vaporizado) sofra a
ação de uma força.
 A força faz com que o gás seja arremessado contra o
projétil, acelerando-o em direção ao exterior.
Cap. 29: Geração de B por i
Lei de Ampère
Nos problemas em que a corrente apresenta alguma simetria o campo magnético
pode ser determinado usando a Lei de Ampère.
 
 B  ds  0iint
 Bds cos    i
0 int
Lei de Ampère
  é o ângulo entre um infinitesimal da curva
Amperiana e o campo magnético local gerado
pelas correntes localizadas no interior da curva.
 Posicione a mão direita com os dedos
apontando no sentido de integração. Uma
corrente que flui no sentido do polegar recebe
o sinal positivo, enquanto que uma corrente no
sentido oposto recebe o sinal negativo.
Cap. 29: Geração de B por i
Lei de Ampère
Campo Gerado por um Fio Longo
 Bds cos    i
0 int
 Escolher uma forma geométrica que delimita
o caminha de integração na qual o campo é
constante, ou apresente uma dependência bem
conhecida (neste caso uma circunferência).
 O ângulo entre B e ds é constante, 0°.
B cos 0 ds  0iint
 0i
B
2r
Campo Magnético gerado
por um fio longo
Cap. 29: Geração de B por i
Lei de Ampère
Campo no Interior de um Fio Longo
 Bds cos    i
0 int
 Nem toda a corrente i contribuirá com o
campo Magnético a uma distância r do centro.
 O ângulo entre B e ds é constante, 0°.
J int  J tot
iint / r 2  i / R 2
ir 2
iint  2
R
ir 2
B 2r  0 2
R
0ir
B
2R 2
Campo Magnético gerado
No interior de um fio longo
Cap. 29: Geração de B por i
Lei de Ampère
Exemplo 29-3) pg. 244
A figura mostra a seção de reta de um cilindro condutor oco de raio interno a = 2,0 cm e
raio externo b = 4,0 cm. O cilindro conduz uma corrente para fora do plano do papel, e o
módulo da densidade de corrente na seção reta é dado por J = cr2, com c = 3,0 x 106 A/m2
e r em metros. Qual é o campo magnético B em um ponto situado a 3 cm de distância do
eixo central do cilindro?
 Bds cos    i
0 int
 Sentido da corrente para fora do papel:
c (r 4  a 4 )
B 2r   0
2
 Cálculo da corrente:

iint   J  nˆdA   cr 2 2rdr
r
c 2r
iint 
4
4 r
a
a
c (r 4  a 4 )

2
B
0 c(r 4  a 4 )
4r
B  2 105 T
 O sinal de negativo indica que o sentido
de que o campo é oposto ao sentido de
circuitação adotado.
Cap. 29: Geração de B por i
Solenóides e Toróides
Solenóide ou Bobina: Dispositivo composto por um condutor enrolado em forma de
espiras muitos próximas. Podem ser formados por uma ou mais camadas de fios
enrolados.
Cap. 29: Geração de B por i
Solenóides e Toróides
Campo no Interior de uma Bobina
 
 B  ds  0iint
 Escolher uma curva Amperiana adequada.
  c   d   a  
 B  ds   B  ds   B  ds   B  ds  0iint
b
a
b
c
d
 As integrais de c até b assim como de a até d se anulam pois o campo é perpendicular
ao caminho de integração. A integral de d até c, que delimita a região externa do
solenóide é nula, pois nessa região o campo magnético é zero.
  d  
 B  ds   B  ds  0 Ni
b
a
B
c
0 Ni
h
h
B  ds  0 Ni
0
B  0 ni
 N = número de espiras.
 h = comprimento da bobina.
 n = número de espiras por unidade de comprimento
Cap. 29: Geração de B por i
Solenóides e Toróides
Toróide: solenóide cilíndrico
que foi encurvado até as
extremidades se tocarem,
formando um anel.
 
 B  ds  0iint
 Por simetria usamos uma circunferência para descrever a simetria do campo no
interior do toróide.
2
B  rd  0 Ni
0
0 Ni
B
2r
Campo Magnético
no interior do Toróide
Cap. 29: Geração de B por i
Solenóides e Toróides
Exemplo 29-3) pg. 247
Um solenóide tem comprimento L = 1,23 m e um diâmetro interno d = 3,55 cm e conduz
uma corrente i = 5,57 A. É formado por 5 camadas de espiras cada uma com 850 espiras.
Qual o valor de B no centro do solenóide?
B  0 ni
 Calcular a densidade linear de espiras do solenóide.
n N/L
5(850)
 3455,3espiras / m
1,23
B  0 ni  24,2mT
Cap. 29: Geração de B por i
Solenóides como um Dipolo Magnético
Campo Magnético de uma Espira ao Longo do Eixo X
0 ids sen( )
dB 
4
r2
 r é cte; i é cte;  é cte;
 r é sempre perpendicular a corrente i ( = 90°).
0 isen(90)
dB 
ds
2

4
r
 Devido à simetria do problema, as componentes Br se cancelam aos pares.
Restam apenas as componentes Bx do campo.
0 i 2R
B
4 r 2
Bx  B cos 
r R x
2
2
2
R
cos   
r
Bx 
R
R2  x2
0
iR
R
2 (R 2  x 2 ) R 2  x 2
 0i
R2
Bx 
2 (R 2  x 2 )3 / 2
Cap. 29: Geração de B por i
Solenóides como um Dipolo Magnético
Campo Magnético de uma Espira ao Longo do Eixo X
 0i
R2
Bx 
2 (R 2  x 2 )3 / 2
Campo Magnético gerado por uma espira ao
longo do eixo x.
 Para x >> R, temos:
Bx 
 0i R 2
2 x3
 Considerando uma bobina de N espiras:
0 Ni R 2
Bx 
2 x 3
Bx 
0 Ni A
2 x 3

Bx 
0 
2x 3
  NiA
Cap. 29: Geração de B por i
Solenóides como um Dipolo Magnético
Campo Magnético de uma Espira ao Longo do Eixo X
 Relembrando o torque de uma bobina:

  B


Campo já existente em
alguma
região
do
espaço!
  Bsen
  NiA
 Agora podemos calcular o momento dipolar magnético de outra forma:
conhecendo o campo gerado pela bobina Bx!



Bx  0 3
2x



2x Bx
3
0
Campo gerado pela bobina
ao longo do eixo x.
Cap. 29: Geração de B por i
A Lei de Biot-Savart
Lista de Exercícios:
3, 5, 7, 11, 13, 17, 21, 28, 31, 33, 37, 41, 43, 47,
48, 53, 55, 59, 63, 69, 87
Referências
HALLIDAY, D.; RESNICK, R.; WALKER, J.; Fundamentos
Eletromagnetismo. 8a ed. Rio de janeiro: LTC, 2009. v3.
de
Física:
TIPLER, P. A.; Física para Cientistas e Engenheiros. 4a ed, LTC, 2000. v2.
SEARS, F.; ZEMANSKY, M.W.; YOUNG, H.; FREEDMAN, R.A.; Física:
Eletromagnetismo. 12a ed. São Paulo: Pearson Addison Wesley, 2008. v3.