Circuitos Elétricos - NS Aulas Particulares

Apostila de Revisão de Eletrodinâmica: 1ª Lei de Ohm, Potência e Energia Elétrica,
Associação de Resistores e Circuito Elétrico
1. (G1 - cftmg 2013) O meio que conduz melhor a eletricidade é a(o)
a) ar, devido à facilidade de propagar o relâmpago.
b) metal, porque possui maior número de cargas livres.
c) plástico, pois deriva-se do petróleo, grande fonte de energia.
d) madeira, uma vez que as árvores atraem raios em dias de tempestade.
2. (Pucrj 2013) O gráfico abaixo apresenta a medida da variação de potencial em função da
corrente que passa em um circuito elétrico.
Podemos dizer que a resistência elétrica deste circuito é de:
a) 2,0 m
b) 0,2 
c) 0,5 
d) 2,0 k
e) 0,5 k
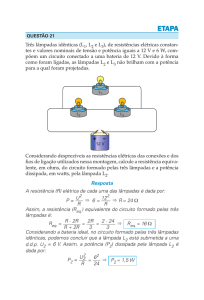
3. (Uerj 2013) Em uma experiência, três lâmpadas idênticas {L1, L2, L3} foram inicialmente
associadas em série e conectadas a uma bateria E de resistência interna nula. Cada uma dessas lâmpadas pode ser individualmente ligada à bateria E sem se queimar.
Observe o esquema desse circuito, quando as três lâmpadas encontram-se acesas:
Em seguida, os extremos não comuns de L1 e L2 foram conectados por um fio metálico,
conforme ilustrado abaixo:
A afirmativa que descreve o estado de funcionamento das lâmpadas nessa nova condição é:
a) As três lâmpadas se apagam.
b) As três lâmpadas permanecem acesas.
c) L1 e L2 se apagam e L3 permanece acesa.
d) L3 se apaga e L1 e L2 permanecem acesas.
4. (Pucrj 2013)
No circuito mostrado na figura, a diferença de potencial entre os pontos B e A vale, em
Volts:
a) 3,0
b) 1,0
c) 2,0
d) 4,5
e) 0,75
5. (G1 - ifsp 2013) Ao entrar em uma loja de materiais de construção, um eletricista vê o
seguinte anúncio:
ECONOMIZE: Lâmpadas fluorescentes de 15 W têm a mesma luminosidade (iluminação)
que lâmpadas incandescentes de 60 W de potência.
De acordo com o anúncio, com o intuito de economizar energia elétrica, o eletricista troca
uma lâmpada incandescente por uma fluorescente e conclui que, em 1 hora, a economia de
energia elétrica, em kWh, será de
a) 0,015.
b) 0,025.
c) 0,030.
d) 0,040.
e) 0,045.
6. (Ufsm 2013) A favor da sustentabilidade do planeta, os aparelhos que funcionam com
eletricidade estão recebendo sucessivos aperfeiçoamentos. O exemplo mais comum são as
lâmpadas eletrônicas que, utilizando menor potência, iluminam tão bem quanto as lâmpadas
de filamento.
Então, analise as afirmativas:
I. A corrente elétrica que circula nas lâmpadas incandescentes é menor do que a que circula
nas lâmpadas eletrônicas.
II. Substituindo uma lâmpada incandescente por uma eletrônica, esta fica com a mesma ddp
que aquela.
III. A energia dissipada na lâmpada incandescente é menor do que na lâmpada eletrônica.
Está(ão) correta(s)
a) apenas I e II. b) apenas II. c) apenas I e III. d) apenas III. e) I, II e III.
7. (Uerj 2013) Ao ser conectado a uma rede elétrica que fornece uma tensão eficaz de 200
V, a taxa de consumo de energia de um resistor ôhmico é igual a 60 W.
Determine o consumo de energia, em kWh, desse resistor, durante quatro horas, ao ser conectado a uma rede que fornece uma tensão eficaz de 100 V.
8. (Unifesp 2013) Observe a charge.
Em uma única tomada de tensão nominal de 110V, estão ligados, por meio de um adaptador, dois abajures (com lâmpadas incandescentes com indicações comerciais de 40W–
110V), um rádio-relógio (com potência nominal de 20W em 110V) e um computador, com
consumo de 120W em 110V. Todos os aparelhos elétricos estão em pleno funcionamento.
a) Utilizando a representação das resistências ôhmicas equivalentes de cada aparelho elétrico como RL para cada abajur, RR para o rádio-relógio e RC para o computador, esboce o
circuito elétrico que esquematiza a ligação desses 4 aparelhos elétricos na tomada (adaptador) e, a partir dos dados da potência consumida por cada aparelho, calcule a corrente
total no circuito, supondo que todos os cabos de ligação e o adaptador são ideais.
b) Considerando que o valor aproximado a ser pago pelo consumo de 1,0kWh é R$0,30 e
que os aparelhos permaneçam ligados em média 4 horas por dia durante os 30 dias do
mês, calcule o valor a ser pago, no final de um mês de consumo, devido a estes aparelhos
elétricos.
9. (G1 - cftmg 2013) Uma pessoa verificou que o ferro elétrico de 1.000 W, por ficar muito
tempo em funcionamento, causa gasto excessivo na sua conta de energia elétrica. Como
medida de economia, ela estabeleceu que o consumo de energia desse aparelho deveria ser
igual ao de um chuveiro de 4.400 W ligado durante 15 minutos. Nessas condições, o tempo
máximo de funcionamento do ferro deve ser, em minutos, igual a
a) 22.
b) 44.
c) 66.
d) 88.
10. (Upe 2013) Ligando quatro lâmpadas de características idênticas, em série, com uma
fonte de força eletromotriz de 220 V, é CORRETO afirmar que a diferença de potencial elétrico em cada lâmpada, em Volts, vale
a) 55
b) 110
c) 220
d) 330
e) 880
11. (Espcex (Aman) 2013) Quatro lâmpadas ôhmicas idênticas A, B, C e D foram associadas e, em seguida, a associação é ligada a um gerador de energia elétrica ideal. Em um dado
instante, a lâmpada A queima, interrompendo o circuito no trecho em que ela se encontra.
As lâmpadas B, C e D permanecem acesas, porém o brilho da lâmpada B aumenta e o brilho
das lâmpadas C e D diminui. Com base nesses dados, a alternativa que indica a associação
formada por essas lâmpadas é:
a)
b)
c)
d)
e)
12. (G1 - cftmg 2012) A figura representa um trecho de um circuito elétrico em que a diferença de potencial entre os pontos A e B vale 12 V.
O valor da intensidade de corrente elétrica i, em ampères, e da resistência elétrica do resistor
R, em ohm, valem, respectivamente,
a) 2,0 e 6,0.
b) 4,0 e 2,0.
c) 6,0 e 2,0.
d) 6,0 e 4,0.
13. (Pucsp 2012) O resistor RB dissipa uma potência de 12 W. Nesse caso, a potência dissipada pelo resistor RD vale
a) 0,75 W
b) 3 W
c) 6 W
d) 18 W
e) 24 W
14. (Enem 2012) Para ligar ou desligar uma mesma lâmpada a partir de dois interruptores,
conectam-se os interruptores para que a mudança de posição de um deles faça ligar ou desligar a lâmpada, não importando qual a posição do outro. Esta ligação é conhecida como
interruptores paralelos. Este interruptor é uma chave de duas posições constituída por um
polo e dois terminais, conforme mostrado nas figuras de um mesmo interruptor. Na Posição
I a chave conecta o polo ao terminal superior, e na Posição II a chave o conecta ao terminal
inferior.
O circuito que cumpre a finalidade de funcionamento descrita no texto é:
a)
b)
c)
d)
e)
15. (Fuvest 2012)
A figura acima representa, de forma esquemática, a instalação elétrica de uma residência,
com circuitos de tomadas de uso geral e circuito específico para um chuveiro elétrico. Nessa
residência, os seguintes equipamentos permaneceram ligados durante 3 horas a tomadas de
uso geral, conforme o esquema da figura: um aquecedor elétrico (Aq) de 990 W, um ferro
de passar roupas de 980 W e duas lâmpadas, L1 e L2, de 60 W cada uma. Nesse período,
além desses equipamentos, um chuveiro elétrico de 4400 W, ligado ao circuito específico,
como indicado na figura, funcionou durante 12 minutos. Para essas condições, determine
a) a energia total, em kWh, consumida durante esse período de 3 horas;
b) a corrente elétrica que percorre cada um dos fios fase, no circuito primário do quadro de
distribuição, com todos os equipamentos, inclusive o chuveiro, ligados;
c) a corrente elétrica que percorre o condutor neutro, no circuito primário do quadro de distribuição, com todos os equipamentos, inclusive o chuveiro, ligados.
NOTE E ADOTE
- A tensão entre fase e neutro é 110 V e, entre as fases, 220 V.
16. (Uff 2012) Um estudante montou o circuito da figura com três lâmpadas idênticas,
A, B e C, e uma bateria de 12V. As lâmpadas têm resistência de 100.
a) Calcule a corrente elétrica que atravessa cada uma das lâmpadas.
b) Calcule as potências dissipadas nas lâmpadas A e B e identifique o que acontecerá com
seus respectivos brilhos (aumenta, diminui ou permanece o mesmo) se a lâmpada C
queimar.
17. (Ufrgs 2012) Considere o circuito a seguir.
No circuito, por onde passa uma corrente elétrica de 4 A, três resistores estão conectados a
uma fonte ideal de força eletromotriz de 20 V.
Os valores da resistência total deste circuito e da resistência RX são, respectivamente,
a) 0,8  e 2,6 .
b) 0,8  e 4,0 .
c) 5,0  e 5,0 .
d) 5,0  e 10,0 .
e) 10,0  e 4,0 .
18. (G1 - utfpr 2012) O chuveiro elétrico esquenta porque, apresenta uma
_______________ que aquece a água, quando passa uma ____________ elétrica. A este
fenômeno chamamos de Efeito ________.
Assinale a única alternativa que completa o texto acima, de forma correta.
a) aceleração, energia potencial, Cascata.
b) energia cinética, força peso, Joule.
c) resistência elétrica, aceleração, Cascata.
d) queda de temperatura, corrente, Joule.
e) resistência elétrica, corrente, Joule.
19. (Espcex (Aman) 2012) Um circuito elétrico é constituído por um resistor de 4 Ω e outro
resistor de 2 Ω. Esse circuito é submetido a uma diferença de potencial de 12 V e a corrente
que passa pelos resistores é a mesma. A intensidade desta corrente é de:
a) 8 A
b) 6 A
c) 3 A
d) 2 A
e) 1 A
TEXTO PARA A PRÓXIMA QUESTÃO:
Uma sala é iluminada por um circuito de lâmpadas incandescentes em paralelo.
Considere os dados abaixo:
− a corrente elétrica eficaz limite do fusível que protege esse circuito é igual a 10 A;
− a tensão eficaz disponível é de 120 V;
− sob essa tensão, cada lâmpada consome uma potência de 60 W.
20. (Uerj 2012) A resistência equivalente, em ohms, de apenas 8 lâmpadas acesas é cerca
de:
a) 30
b) 60
c) 120
d) 240
21. (Fuvest 2011) O filamento de uma lâmpada incandescente, submetido a uma tensão U,
é percorrido por uma corrente de intensidade i. O gráfico abaixo mostra a relação entre i e
U.
As seguintes afirmações se referem a essa lâmpada.
I. A resistência do filamento é a mesma para qualquer valor da tensão aplicada.
II. A resistência do filamento diminui com o aumento da corrente.
III. A potência dissipada no filamento aumenta com o aumento da tensão aplicada.
Dentre essas afirmações, somente
a) I está correta.
b) II está correta.
c) III está correta.
d) I e III estão corretas.
e) II e III estão corretas.
22. (Udesc 2011) Um fio condutor foi submetido a diversas voltagens em um laboratório. A
partir das medidas dessas voltagens e das correntes que se estabeleceram no condutor, foi
possível obter o gráfico a seguir.
O valor da resistência desse condutor é:
a) 32 Ω
b) 0,02 Ω
c) 150 Ω
d) 250 Ω
e) 50 Ω
23. (Ufpr 2011) Um pesquisador produziu um novo material e, para investigar possíveis
aplicações tecnológicas, estudou o comportamento elétrico de um objeto cilíndrico feito
com esse material. Aplicaram-se diversos valores de diferenças de potencial ∆V a esse objeto e mediu-se a corrente elétrica i que circulou por ele. Foi obtido então o gráfico ao lado:
Com base nesse gráfico, considere as seguintes afirmativas:
1. O objeto apresenta comportamento ôhmico apenas para diferenças de potencial entre 0 V
e 1 V.
2. Quando submetido a uma diferença de potencial de 4 V, a resistência elétrica do objeto
vale R = 20  .
3. Para diferenças de potencial entre 1 V e 3 V, a resistência elétrica do objeto é constante.
4. Quando aplicada uma diferença de potencial de 2 V, a potência elétrica dissipada pelo
objeto é igual a 1 W.
Assinale a alternativa correta.
a) Somente as afirmativas 1, 2 e 4 são verdadeiras.
b) Somente as afirmativas 2 e 3 são verdadeiras.
c) Somente as afirmativas 1 e 2 são verdadeiras.
d) Somente as afirmativas 1 e 3 são verdadeiras.
e) As afirmativas 1, 2, 3 e 4 são verdadeiras.
24. (Enem 2011) Um curioso estudante, empolgado com a aula de circuito elétrico que assistiu na escola, resolve desmontar sua lanterna. Utilizando-se da lâmpada e da pilha, retiradas do equipamento, e de um fio com as extremidades descascadas, faz as seguintes ligações
com a intenção de acender a lâmpada:
Tendo por base os esquemas mostrados, em quais casos a lâmpada acendeu?
a) (1), (3), (6)
b) (3), (4), (5)
c) (1), (3), (5)
d) (1), (3), (7)
e) (1), (2), (5)
25. (Uerj 2011) No circuito abaixo, o voltímetro V e o amperímetro A indicam, respectivamente, 18 V e 4,5 A.
Considerando como ideais os elementos do circuito, determine a força eletromotriz E da
bateria.
26. (Uftm 2011) No circuito mostrado no diagrama, todos os resistores são ôhmicos, o gerador e o amperímetro são ideais e os fios de ligação têm resistência elétrica desprezível.
A intensidade da corrente elétrica indicada pelo amperímetro, em A, é de
a) 3.
b) 4.
c) 8.
d) 12.
e) 15.
27. (Ufu 2011) Considere um circuito elétrico formado por uma fonte ideal com força eletromotriz (fem) de 18 V e três resistências R1  2,00, R2  5,00 e R3  1,25 , como mostra a
figura abaixo.
A corrente no circuito é:
a) 6,00 A
b) 12,00 A
c) 2,20 A
d) 4,00 A
28. (Upe 2011) No circuito elétrico a seguir, considere um gerador de força eletromotriz
ε  18V e resistência interna igual a 1Ω . As resistências dos condutores de alimentação são
desprezíveis.
Analise as afirmativas a seguir e conclua.
( ) A resistência equivalente entre os pontos a e c do circuito vale 5Ω .
( ) A corrente elétrica que circula no gerador tem intensidade igual a 3A.
( ) A potência dissipada pelo resistor colocado entre os pontos a e b do circuito é igual à
potência dissipada pelos resistores colocados entre os pontos a e c do circuito.
( ) A diferença de potencial elétrico entre os pontos a e c vale 18 V.
29. (Ufrgs 2011) Considere o circuito abaixo.
Neste circuito, todos os resistores são idênticos, e C1 e C2 são dois interruptores que podem
estar abertos ou fechados, de acordo com os esquemas numerados a seguir.
C1 C2
C1 C2
C1 C2
C1 C2
aberto
fechado X X
(1)
aberto X X
fechado
(2)
aberto X
X
fechado
(3)
X
aberto
fechado X
(4)
Assinale a alternativa que apresenta corretamente o ordenamento dos esquemas de ligação,
em ordem crescente da corrente elétrica que passa no resistor R4 .
a) (4) – (2) – (3) – (1)
b) (1) – (3) – (2) – (4)
c) (2) – (4) – (3) – (1)
d) (2) – (3) – (4) – (1)
e) (3) – (2) – (1) – (4)
30. (Pucrj 2010) Três resistores idênticos são colocados de tal modo que dois estão em série
entre si e ao mesmo tempo em paralelo com o terceiro resistor. Dado que a resistência efetiva é de 2, quanto vale a resistência de cada um destes resistores Ohms ( Ω )?
a) 100 Ω
b) 30 Ω
c) 1 Ω
d) 10 Ω
e) 3 Ω
31. (Pucrj 2010) Calcule a resistência do circuito formado por 10 resistores de 10 k Ω , colocados todos em paralelo entre si, e em série com 2 resistores de 2 k Ω , colocados em paralelo.
a) 1 k Ω
b) 2 k Ω
c) 5 k Ω
d) 7 k Ω
e) 9 k Ω
32. (Ufsc 2010) Nos circuitos a seguir, A e B são duas lâmpadas cujos filamentos têm resistências iguais; R é a resistência de outro dispositivo elétrico; ε é uma bateria de resistência
elétrica desprezível; e I é um interruptor aberto.
Sabendo-se que o brilho das lâmpadas cresce quando a intensidade da corrente elétrica aumenta, é CORRETO afirmar que:
01) no circuito 1, a lâmpada A brilha mais do que a B.
02) no circuito 2, as lâmpadas A e B têm o mesmo brilho.
04) no circuito 3, uma das lâmpadas brilha mais do que a outra.
08) no circuito 4, a lâmpada B brilha mais do que a A.
16) no circuito 5, se o interruptor I for fechado, aumenta o brilho da lâmpada B.
33. (Ufg 2010) Na figura, são apresentadas as resistências elétricas, em ohms, do tecido
conjuntivo em cada região do corpo humano. Uma pessoa descalça apoiada sobre os dois
pés na terra toca acidentalmente, com uma das mãos, um cabo elétrico de tensão 220 V em
relação à terra.
Considerando o exposto e que a corrente flui apenas pelo tecido mencionado, calcule:
a) a resistência imposta pelo corpo à passagem da corrente elétrica;
b) a corrente elétrica total.
34. (Uerj 2009) Um circuito empregado em laboratórios para estudar a condutividade elétrica de soluções aquosas é representado por este esquema:
Ao se acrescentar um determinado soluto ao líquido contido no copo, a lâmpada acende,
consumindo a potência elétrica de 60 W.
Nessas circunstâncias, a resistência da solução, em ohms, corresponde a cerca de:
a) 14
b) 28
c) 42
d) 56
35. (Puc-rio 2009)
No circuito apresentado na figura, onde a tensão da bateria é 12 V, R1 = 5Ω, R2 = 2Ω, R3 =
2Ω, podemos dizer que a corrente medida pelo amperímetro A colocado no circuito é:
a) 1 A.
b) 2 A.
c) 3 A.
d) 4 A.
e) 5 A.
36. (Ufsm 2008)
Chama-se "gato" uma ligação elétrica clandestina entre a rede e uma residência.
Usualmente, o "gato" infringe normas de segurança, porque é feito por pessoas não especializadas. O choque elétrico, que pode ocorrer devido a um "gato" malfeito, é causado por
uma corrente elétrica que passa através do corpo humano.
Considere a resistência do corpo humano como 105Ω para pele seca e 103Ω para pele molhada.
Se uma pessoa com a pele molhada toca os dois polos de uma tomada de 220 V, a corrente
que a atravessa, em A, é
a) 2,2 × 105
b) 2,2 × 103
c) 4,5
d) 2,2 × 10-1
e) 2,2 ×10-3
37. (Puc-rio 2008) Três resistores idênticos de R = 30 Ω estão ligados em paralelo com
uma bateria de 12 V. Pode-se afirmar que a resistência equivalente do circuito é de
a) Req = 10 Ω, e a corrente é 1,2 A.
b) Req = 20 Ω, e a corrente é 0,6 A.
c) Req = 30 Ω, e a corrente é 0,4 A.
d) Req = 40 Ω, e a corrente é 0,3 A.
e) Req = 60 Ω, e a corrente é 0,2 A.
38. (Fatec 2007) Um resistor ôhmico, de resistência R = 20Ω, submetido à ddp de 200V e
percorrido por uma corrente elétrica de intensidade 10 A e dissipa uma potência de 2000W.
Se o mesmo resistor for submetido a ddp de 100V, a intensidade da corrente que o percorrerá, em amperes, e a potência que dissipará, em watts, serão, respectivamente,
a) 10 e 1000.
b) 10 e 500.
c) 5 e 4000.
d) 5 e 2000.
e) 5 e 500.
39. (G1 - cftmg 2005) Uma lâmpada, ligada em uma tomada de 127 V, dissipa uma potência de 60 W e tem uma vida média de 750 h. Ao final desse tempo, ela terá consumido uma
quantidade de energia elétrica, em kWh, igual a
a) 45.
b) 60.
c) 127.
d) 750.
40. (Unesp 2002) As companhias de eletricidade geralmente usam medidores calibrados em
quilowatt-hora (kWh). Um kWh representa o trabalho realizado por uma máquina desenvolvendo potência igual a 1 kW durante 1 hora. Numa conta mensal de energia elétrica de uma
residência com 4 moradores, leem-se, entre outros, os seguintes valores:
CONSUMO (kWh) - 300
TOTAL A PAGAR (R$) - 75,00
Cada um dos 4 moradores toma um banho diário, um de cada vez, num chuveiro elétrico de
3 kW. Se cada banho tem duração de 5 minutos, o custo ao final de um mês (30 dias) da
energia consumida pelo chuveiro é de
a) R$ 4,50.
b) R$ 7,50.
c) R$ 15,00.
d) R$ 22,50.
e) R$ 45,00.
Gabarito:
Resposta da questão 1:
[B]
Os melhores condutores de eletricidade são os metais porque possuem os elétrons da camada mais externa mais fracamente ligados ao núcleo, sendo facilmente transportados, quando
se estabelece uma diferença de potencial entre os terminais do condutor.
Resposta da questão 2:
[D]
Primeira Lei de OHM
V  R.i  12  Rx6  R  2,0k
Resposta da questão 3:
[C]
Quando o fio metálico é ligado como mostrado na segunda figura, as lâmpadas L1 e L2 entram em curto circuito, apagando. A lâmpada L3 permanece acesa, com brilho mais intenso
que antes.
Resposta da questão 4:
[C]
A resistência equivalente do circuito é:
R  1  1/ /1  1  0,5  1,5
A corrente no circuito é:
V  R.i  3  1,5.i  i  2,0A
A ddp procurada é:
V  R.i  VAB  1x2  2,0V
Resposta da questão 5:
[E]
Dados: P1 = 60 W = 0,06 kW; P2 = 15 W = 0,015 kW;
Δt
= 1 h.
Calculando o consumo de energia de cada lâmpada em 1 hora:
E1  0,06  1  0,06 kW  h
Δ E  P Δt  
 ΔE  E1  E2  0,06  0,015 
E2  0,015  1  0,015 kW  h
ΔE  0,045 kW  h.
Resposta da questão 6:
[B]
[I]. Incorreta. De acordo com o próprio enunciado, as lâmpadas eletrônicas utilizam menor
potência. Da expressão da potência elétrica (P = U i), se estão ligadas à mesma fonte, a
ddp (U) é a mesma para as duas lâmpadas, logo pela de menor potência (eletrônica) circula menor corrente (i).
[II]. Correta. A ddp é estabelecida pela rede de distribuição.
[III]. Incorreta. Usando boa vontade e bom senso, suponhamos que os tempos de operação
(Δt) sejam iguais. Assim, da expressão da energia (E) consumida por um dispositivo de potência P (E  PΔt), a lâmpada que utiliza maior potência consome maior energia, no caso a
incandescente.
Resposta da questão 7:
Dados nominais fornecidos no enunciado:
U  200V P  60w
A partir destes dados, temos:
E  P  Δt  15.103 kω  4 h 
neste resistor é dada por:
U2
1002
3.10000


R
2000
 2000 
 3 


30
P
 P  15w
2
P
A energia consumida em 4 horas é dada por:
E  P  Δt  15.103 kw   4 h 
 E  0,06kwh
Resposta da questão 8:
a) Os aparelhos mencionados estão todos ligados diretamente à mesma fonte de tensão,
portanto estão todos em paralelo.
A potência total dissipada é: P = (40 + 40 + 20 + 120) = 220 W.
Aplicando a definição de potência elétrica:
PU I  I
b) Dados:
Δt =
P 220

U 110
 I  2 A.
430 = 120 h; tarifa do kWh, c = R$ 0,30; P = 220 W = 0,22 kW.
O valor a ser pago (C) é :
C  P Δt c  0,22  120  0,30
C  R$ 7,92 .

Resposta da questão 9:
[C]
Dados: Pf = 4.400 W;
Δt f =
15 min; Pc = 1.000 W
Para um mesmo consumo de energia, temos:
Ef  Ec
 Pf Δt f  Pc Δt c
 Δt f 
Pc Δtc 4.400  15

Pf
1.000

Δt f  66 min.
Resposta da questão 10:
[A]
Quando resistores são ligados em série a ddp nos extremos da associação é a soma das ddp
em cada elemento. Como os elementos são idênticos, as ddp também serão. Portanto:
4V  220  V  55 V.
Resposta da questão 11:
[C]
Se A queima e as outras não se apagam, elas não podem estar em série, e, se o brilho delas
se altera, elas não podem estar as quatro em paralelo. Como o brilho de B aumenta, a corrente em B aumenta; como o brilho de C e D diminui, a corrente nelas diminui, implicando
que a resistência equivalente do circuito aumenta. Essas análises nos levam à alternativa
[C].
Resposta da questão 12:
[D]
Como os dois resistores estão em paralelo, a ddp, U = 12 V, é a mesma nos dois ramos.
Aplicando a 1ª lei de Ohm:
12  2 i  i  6 A.
UR i 
12  R 3  R  4 Ω.
Resposta da questão 13:
[C]
Dados: E = 24 V; I = 1 A; iA = 0,5 A; PB = 12 W; iC = 0,25 A.
Como nos dois ramos superiores a corrente se divide igualmente (0,5 A em cada ramo), as
resistências têm mesmo valor. Assim:
RA  8 Ω.
O resistor RB dissipa potência PB = 12 W, com corrente I = 1 A. Da expressão da potência
elétrica dissipada num resistor:
2
PB  RB I2  12  RB 1
 RB  12 Ω.
Aplicando a lei de Ohm-Pouillet:
R

8

E  Req I  E   A  RB  RCD  I  24    12  RCD 1 
2

 2

RCD  8 Ω.
A ddp nesse ramo é:
UCD  RCD I  8 1  UCD  8
A corrente (iD) em RD é:
V.
iD  iC  I  iD  0,25  1  iD  0,75 A.
A potência dissipada em RD por ser calculada por:
PD  UCD iD  8  0,75   PD  6 W.
Resposta da questão 14:
[E]
O único circuito que fecha tanto para a posição I como para a posição II é o circuito da alternativa [E].
Resposta da questão 15:
a) A energia total consumida é o somatório das energias consumidas pelos aparelhos. Da
expressão da potência:
E
12
 E  P Δt  990  980  2  60   W  3h  4.400W 
h  E  7.150 Wh 
Δt
60
E  7,15 kWh.
P
b) A figura a seguir mostra um esquema simplificado desse circuito, representando as tomadas como fontes de corrente contínua e todos os dispositivos como resistores.
Da expressão da potência elétrica:
PU i  i
P
U
Apliquemos essa expressão em cada dispositivo e a lei dos nós em A, B e C no circuito
primário.
Nó A:
Nó C:
c) Nó B:
4.400 990

 20  9  i1  29A.
220 110
4.400
60 980
12 98
110
i2  iC  2iL  iF 
2

 20 

 20 
 i 2  30A.
220
110 110
11 11
11
i1  iC  iA 
iN  i1  i2  iN  29  30  i N 1 A.
Resposta da questão 16:
a) Dados: U = 12 V; R = 100 .
A resistência equivalente do circuito é:
Req  100 
100
2
 R eq  150 Ω.
Aplicando a lei de Ohm-Pouillet:
URI  I
eq
12
150
 I  0,08 A.
Assim:
iA  I  0,08 A;


I
iB  iC   0,04 A.

2
b) Calculemos as potências dissipadas para o caso do item anterior:
2
PR i
P  100  0,08 2  0,64 W;
 A

2
PB  PC  100  0,04   0,16 W.
Se a lâmpada C queimar, as lâmpadas A e B ficam em série, submetidas à tensão U’ = 6 V
cada uma.
As novas potências dissipadas serão:
2
P
U'
R
 PA'  PB' 
62
 0,36 W.
100
Comparando os valores obtidos, concluímos que o brilho da lâmpada A diminui e o brilho
da lâmpada B aumenta.
Resposta da questão 17:
[D]
Da Lei de Ohm-Pouillet:
E  Req I  20  Req  4 
 Req  5 .
Os dois resistores do ramo de cima estão em série, totalizando uma resistência de
dois ramos estão em paralelo. Usando a regra do produto pela soma:
Req 
10  R x
10  R x
 5
10  R x
10  R x
 10  R x  50  5  R x
10 .
Os
 5  R x  50 
R x  10 .
Resposta da questão 18:
[E]
O chuveiro elétrico apresenta um RESISTOR que possui uma resistência elétrica. O que
aquece a água é o calor liberado no resistor pela passagem de corrente elétrica. A esse fenômeno damos o nome de Efeito Joule.
Resposta da questão 19:
[D]
Como a corrente é a mesma, os resistores estão ligados em série e sua resistência equivalente é a soma das resistências de cada um.
Req  R1  R2  6 Ω
Pela Primeira Lei de Ohm, temos:
V  R.i  12  6i  i  2,0A
Resposta da questão 20:
[A]
P
V2
120 2
14400
 8  60 
R 
 30Ω
R
R
480
Resposta da questão 21:
[C]
Para maior clareza, destaquemos dois pontos, A e B, do gráfico:
I. Incorreta. Quando a resistência é constante, tensão e corrente são diretamente proporcionais, portanto o gráfico é uma reta que passa pela origem.
II. Incorreta. Calculemos a resistência para os pontos, A e B, destacados na figura:
RA 
UA
iA

2
 13,3
0,15
.
RB 
UB
iB

6
 24
0, 25
.
Portanto, a resistência aumenta com o aumento da corrente.
III. Correta. Calculemos as potências dissipadas para os valores dos pontos destacados:
PA = UA iA = 2 (0,15) = 0,3 W.
PB = UB iB = 6 (0,25) = 1,5 W.
PB > PA  a potência dissipada no filamento aumenta com o aumento da tensão aplicada.
Resposta da questão 22:
[E]
R
V 32

 50
i
0,6
Resposta da questão 23:
[C]
1. Certo, pois a corrente está proporcional a ddp.
2. Certo. V = Ri  4 = R x 0,2  R = 20
3. Falso.
Para
Para
V
1

 10
i
0,1
V
3
V  3V  R  
 30
i
0,1
V  1V  R 
4. Falso.
P  V.i  2  0,1  0,2W
Resposta da questão 24:
[D]
Observemos a figura:
Ela mostra que, para uma lâmpada incandescente acender, um terminal da pilha deve estar
em contato com a rosca e, o outro, com o pino (base), como ocorre em (1), (3) e (7).
Resposta da questão 25:
Dados: UCD = UBE = 18 V; i2 = 4,5 A.
1ª Solução:
No resistor R3:
UCD = R3 i3  18 = 12 i3  i3 = 1,5 A.
A corrente total é:
i = i2 + i3 = 4,5 + 1,5  i = 6 A.
Aplicando a Lei de Kirchoff na malha ABCDEFA:
E – R1 i – UCD – R4 i = 0  E = 3 (6) + 18 + 4 (6)  E = 60 V.
2ª Solução:
No resistor R3:
UCD = R3 i3  18 = 12 i3  i3 = 1,5 A.
No resistor R2:
UBE = R2 i2  18 = R2 (4,5)  R2 = 4 Ω .
A corrente total é:
i = i2 + i3 = 4,5 + 1,5  i = 6 A.
Calculando a resistência equivalente do circuito:
Req =
R1 
R 2  R3
12  4
 R 4  R eq  3 
4 
R2  R3
12  4
Aplicando a Lei de Ohm-Pouillet:
E = Req i  E = 10 (6)  E = 60 V.
Req = 10 .
Resposta da questão 26:
[E]
O circuito abaixo é equivalente ao dado:
Como mostrado, a resistência equivalente é 4 Ω .
Aplicando a lei de Ohm-Pouillet:
E = Req i  60 = 4 i  i = 15 A.
Resposta da questão 27:
[A]
Req  R1  R2 / /R3
Req  R1 
R2 .R3
R 2  R3
5  1,25
6,25
2
 3Ω
5  1,25
6,25
Lei de Ohm: V  Ri  18  3i  i  6,0A
Req  2 
Resposta da questão 28:
V V V F.
A resistência de 6Ω está em curto e pode ser retirada do circuito.
(V) Rac  10 / /(8  2)  5Ω .
(V) V  R.i  18  (1 5)i  i  3,0A
(V) A corrente que passa no resistor de 10Ω é metade da corrente total, pois as resistências
dos dois braços são iguais. Portanto, as potências dissipadas são iguais.
3
2
(F) V  Ri  V  10x  15W
Resposta da questão 29:
[C]
A corrente em R4 será maior quando a resistência do restante do circuito for menor.
R
.
2
(2) R2 ligada R3 desligada  (Req )2  (R1  R2 )  2R .
(1) R2 em curto, R3 ligada  (Req )1  (R1 / /R3 ) 
(3) As duas ligadas  (Req )3  (R1  R2 ) / /R3 
(4) As duas desligadas  (Req )4  R1  R .
2RxR 2R

.
2R  R
3
A ordem crescente de corrente será a ordem decrescente de resistência. Portanto, (2), (4), (3)
e (1).
Resposta da questão 30:
[E]
A associação é a representada na figura a seguir.
No ramo em série, a resistência equivalente é 2 R.
Na associação em paralelo, fazendo a regra do produto/soma, temos:
2R  R
2R2
2
2 
2R  R
3R
2 R = 6 R = 3 Ω.
Resposta da questão 31:
[B]
O circuito sugerido está mostrado na figura a seguir. Sabemos que para n resistores idênticos em paralelo a resistência equivalente é:
RP =
R
n
.
Assim para os dois conjuntos em paralelo:
R1 =
10
1Ω
10
e R2 =
2
2
= 1Ω.
Como os dois conjuntos estão em série, a resistência equivalente é:
Req = R1 + R2 = 2 Ω .
Resposta da questão 32:
02 + 08 = 10
01) Falsa. As duas lâmpadas estão em série, sendo percorridas pela mesma corrente, apresentando, portanto o mesmo brilho.
02) Correta. Mesma justificativa do item anterior.
04) Falsa. Como elas têm resistências iguais, a corrente total gerada pela bateria é dividida
igualmente em duas correntes parciais que atravessam a lâmpada fazendo com que elas
brilhem com mesma intensidade.
08) Correta. Há o resistor de resistência R em série com a lâmpada A, fazendo com que a
corrente no ramo inferior seja menor do que a corrente no ramo superior. Assim, a lâmpada A brilha menos que a lâmpada B.
16) Falsa. Ao fechar o interruptor, a lâmpada B entra em curto-circuito e apaga.
Resposta da questão 33:
a) O circuito equivalente possui um ramo em série e dois ramos em paralelo, que correspondem ao trajeto pelas pernas.
A resistência equivalente é:
Req = 500 + 270 + 110 + 100 + 13 +
b)
i
U
220

Req 1248
 i  0,176 A.
50  140  320
2
= 993 + 255 =1.248  .
Resposta da questão 34:
[A]
Resolução
Levando em conta a potência e a ddp na lâmpada
P = U.i  60 = 120.i  i = 0,5 A
Esta corrente viaja pelos fios condutores e logo também é a corrente na solução.
U = r.i  (127 – 120) = r.0,5  r = 7/0,5 = 14 
Resposta da questão 35:
[B]
Resolução
Equivalente entre os resistores 2 e 3
 2.2  4
 =1
R’ =
 2  2 4
Para todo o circuito
U = r.i
12 = (5 + 1).i
12 = 6.i  i =
12
6
=2A
Resposta da questão 36:
[D]
Resolução
U = R.i
220 = 103.i  i = 220.10-3 = 2,2.10-1 A
Resposta da questão 37:
[A]
Resposta da questão 38:
[E]
Resposta da questão 39:
[A]
Resposta da questão 40:
[B]