Lista 1 - Departamento de Física

CF059 – Física I
2S-2016
Lista de Problemas 1
Evaldo
Grandezas e Unidades, Cinemática
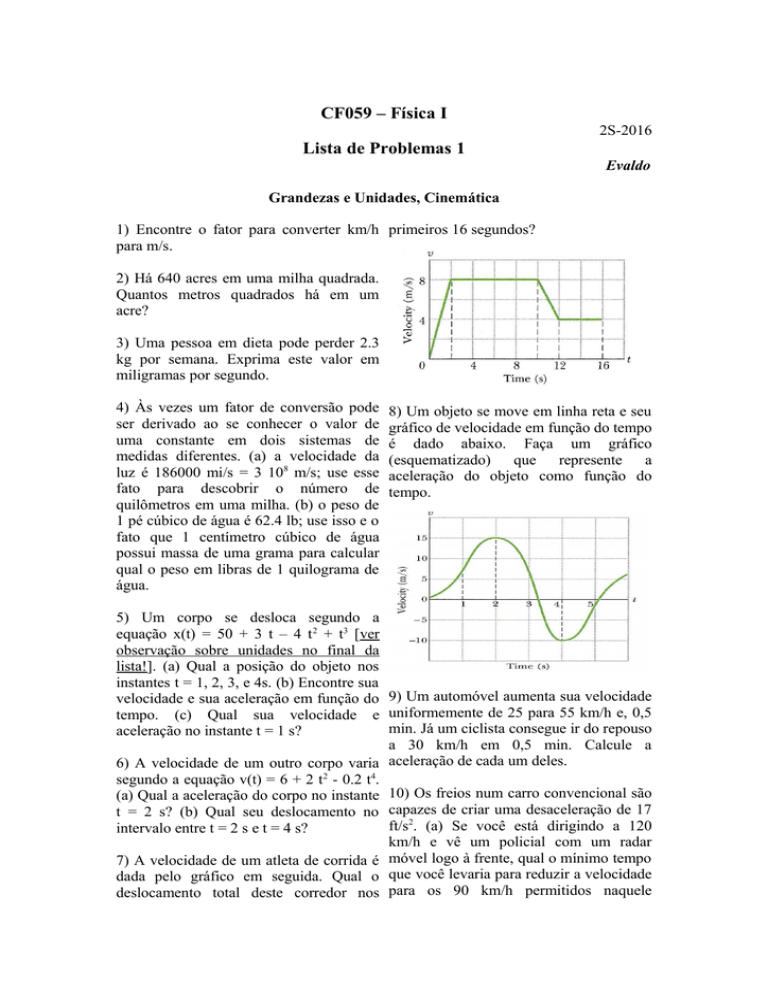
1) Encontre o fator para converter km/h primeiros 16 segundos?
para m/s.
2) Há 640 acres em uma milha quadrada.
Quantos metros quadrados há em um
acre?
3) Uma pessoa em dieta pode perder 2.3
kg por semana. Exprima este valor em
miligramas por segundo.
4) Às vezes um fator de conversão pode
ser derivado ao se conhecer o valor de
uma constante em dois sistemas de
medidas diferentes. (a) a velocidade da
luz é 186000 mi/s = 3 108 m/s; use esse
fato para descobrir o número de
quilômetros em uma milha. (b) o peso de
1 pé cúbico de água é 62.4 lb; use isso e o
fato que 1 centímetro cúbico de água
possui massa de uma grama para calcular
qual o peso em libras de 1 quilograma de
água.
8) Um objeto se move em linha reta e seu
gráfico de velocidade em função do tempo
é dado abaixo. Faça um gráfico
(esquematizado) que represente a
aceleração do objeto como função do
tempo.
5) Um corpo se desloca segundo a
equação x(t) = 50 + 3 t – 4 t 2 + t3 [ver
observação sobre unidades no final da
lista!]. (a) Qual a posição do objeto nos
instantes t = 1, 2, 3, e 4s. (b) Encontre sua
velocidade e sua aceleração em função do 9) Um automóvel aumenta sua velocidade
tempo. (c) Qual sua velocidade e uniformemente de 25 para 55 km/h e, 0,5
min. Já um ciclista consegue ir do repouso
aceleração no instante t = 1 s?
a 30 km/h em 0,5 min. Calcule a
6) A velocidade de um outro corpo varia aceleração de cada um deles.
segundo a equação v(t) = 6 + 2 t2 - 0.2 t4.
(a) Qual a aceleração do corpo no instante 10) Os freios num carro convencional são
t = 2 s? (b) Qual seu deslocamento no capazes de criar uma desaceleração de 17
ft/s2. (a) Se você está dirigindo a 120
intervalo entre t = 2 s e t = 4 s?
km/h e vê um policial com um radar
7) A velocidade de um atleta de corrida é móvel logo à frente, qual o mínimo tempo
dada pelo gráfico em seguida. Qual o que você levaria para reduzir a velocidade
deslocamento total deste corredor nos para os 90 km/h permitidos naquele
trecho? (b) Quanto seu carro se desloca
durante esse intervalo de tempo?
16) Gotas de chuva provindas de uma
nuvem a 1700 m de altitude atingem a
11) Duas estações do metrô de São Paulo superfície da Terra. Se não houvesse
são separadas por 1100 m. Se o trem do resistência do ar, qual a velocidade com
metrô acelera a 1,2 m/s 2 a partir do que as gotas de chuva atingiriam a
repouso na primeira metade do percurso, e superfície? Seria seguro andar na chuva
desacelera a -1,2 m/s2 na segunda metade, nessa situação?
calcule: (a) o tempo total de percurso de
uma estação para a outra; e (b) a 17) Um corpo cai da altura de 50 m
velocidade máxima atingida. (c) Faça um partindo do repouso. Qual a distância
gráfico de x(t), v(t) e a(t) para este percorrida no último segundo de queda?
movimento entre as estações.
18) Um parafuso escapa da base de um
12) No instante em que um semáforo elevador que se move para cima com
muda para luz verde, um automóvel inicia velocidade constante de 6 m/s. O parafuso
seu movimento, a partir do repouso, com atinge o fundo do fosso do elevador em 3
aceleração de 2,2 m/s2. No mesmo s. (a) Qual a altura em que o elevador se
instante, um caminhão que se deslocava encontrava quando o parafuso se soltou?
com velocidade constante de 9,5 m/s (b) Qual a velocidade do parafuso quando
ultrapassa o automóvel. (a) A que atinge o chão do fosso?
distância do semáforo o automóvel vai
ultrapassar o caminhão? (b) Quão rápido 19) Uma bolinha de argila úmida cai de
se desloca o automóvel neste instante da uma altura de 15 m, a partir do repouso.
ultrapassagem?
Ela atinge o solo 20 ms antes de parar
completamente. Qual a aceleração média
13) Dois trens, um viajando a 72 km/h e da bolinha durante o tempo em que esteve
outro a 144 km/h estão viajando nos em contato com o chão (até parar
mesmos trilhos e em rota de colisão. completamente)? Trate a bolinha como
Quando estão separados por 950 m, cada uma partícula.
condutor vê o outro trem em sua direção e
acionam o freio. Como os freios dos trens 20) Encontre a magnitude e a direção dos
conseguem causar uma desaceleração de 1 seguintes vetores: (a) A = 5i + 3j; (b) B =
m/s2, determine se haverá uma colisão.
10i – 7j. [ver observação sobre vetores no
final da lista]
14) Alguns jogadores de futebol, como o
lateral Roberto Carlos e o ponta Éder 21) Dois vetores são dados por A = 4i (canhotos que passaram por um glorioso 3j; (b) B = 6i + 8j. Encontre a magnitude
time nacional) conseguiam chutar a bola e a direção de: (a) A, (b) B, (c) A + B, (d)
com uma velocidade de 130 km/h. Se a A – B, e (e) B – A.
bola fosse chutada para cima, (a) qual
seria a altura máxima atingida e (b) 22) Um canhão é elevado a um ângulo de
quanto tempo a bola permaneceria no ar 45o e dispara uma bala com velocidade de
após o chute?
300 m/s. (a) Que altura a bala atinge? (b)
Quanto tempo a bala fica no ar? (c) Qual
15) Numa obra, uma chave inglesa atinge o alcance do tiro?
o chão com uma velocidade de 24 m/s. (a)
De que altura ela foi largada por acidente? 23) Uma pedra é lançada em direção a um
(b) Por quanto tempo ela ficou caindo penhasco de altura h com uma velocidade
antes de atingir o chão?
inicial de 42 m/s e direcionada a 60 o com
a horizontal, como mostra a figura. A
pedra atinge o ponto A 5,5 s após o
lançamento. Encontre (a) a altura h do
penhasco; (b) a velocidade da pedra no
momento do impacto; e (c) a altura
máxima H que a pedra atinge na vertical.
que objetos no equador tivessem uma
aceleração centrípeta de 9,8 m/s2?
27) Qual é a hora entre 9 horas e 10 horas
em que o ponteiro dos minutos de um
relógio coincide com o das horas?
28) Centrífugas de alta velocidade
(ultracentrífugas) operam na faixa de
60000 rotações por minuto. (a) Se o raio
da centrífuga for 20 cm, qual o módulo da
aceleração na circunferência? (b) Qual a
razão deste valor para g (aceleração da
24) Um projétil é lançado no ar do topo de gravidade)?
um penhasco de 200 m de altura. Sua
velocidade inicial é 60 m/s a um ângulo 29) Na figura abaixo, a roda maior (30 cm
de 60o com a horizontal. Qual o alcance de raio) transmite seu movimento à menor
(20 cm de raio) através da correia sem fim
do projétil?
C, que permanece sempre esticada e sem
25) O alcance de um projétil depende não deslizar. A roda maior, partindo do
apenas do módulo da velocidade inicial e repouso com aceleração angular uniforme,
do ângulo de lançamento, mas também da leva 1 minuto para atingir sua velocidade
aceleração da gravidade local. Em 1936, de regime permanente, e efetua um total
Jesse Owens estabeleceu o recorde de 540 rotações durante esse intervalo.
olímpico de salto em distância (8,09 m) Calcule a velocidade angular da roda
nos jogos olímpicos de Berlin (g = 9,8128 menor e a velocidade linear da correia
m/s2). Assumindo a mesma situação após atingido o regime permanente.
inicial deste salto, qual teria sido o valor
do recorde se o atleta estivesse
competindo em Melbourne (g = 9,7999
m/s2)?
26) (a) Qual é a aceleração centrípeta de
um objeto sobre o equador, devida à
rotação da Terra? (b) Qual deveria ser o
período de rotação de nosso planeta para
Utilizar g = 9.8 m/s2 quando necessário.
Observação sobre unidades
Por questões de estética, sempre que escrevi alguma equação horária, de
velocidade ou algum vetor, omiti as unidades que deveriam vir explicitadas. Por
exemplo, no problema 1 a função da posição deveria ser escrita como:
x(t) = 50 m + 3 m/s t – 4 m/s2 t2 + 1 m/s3 t3,
de forma que as unidades de cada termo resultassem em metros (a unidade de x).
Porém isto é muito maçante e praticamente nenhum livro texto carrega essa notação,
assumindo implicitamente que a análise dimensional é por conta do leitor.
Nesta lista, e nas próximas que virão, se as unidades não estiverem
explicitamente colocadas nas funções horárias, balanços de força, diagramas de
colisão e similares, fica convencionado a partir de agora que utilizarei sempre as
unidades do Sistema Internacional (para o que nos interessa, quilograma, metro e
segundo).
Observação sobre notação vetorial
Conforme comentado em sala, uso nas listas a notação semelhante à adotada
nos livros texto: vetores escritos em negrito (x, v, a) e seus módulos (escalares) em
caracteres normais (x, v, a). As setinhas sobre as grandezas vetoriais ficam para a sala
de aula e para a resolução e correção das provas.