Document

UNIVERSIDADE FEDERAL DE VIÇOSA
ESTUDO DA ENERGIZAÇÃO, CURTO E DE SITUAÇÕES DE
CARGA QUE OCORREM NA LINHA DE TRANSMISSÃO
JAGUARA-TAQUARIL.
Thiago Cornélio da Fonseca
Orientador: José Tarcísio de Resende
VIÇOSA
2010
Thiago Cornélio da Fonseca
ESTUDO DA ENERGIZAÇÃO, CURTO E DE SITUAÇÕES DE
CARGA QUE OCORREM NA LINHA DE TRANSMISSÃO
JAGUARA-TAQUARIL.
Monografia apresentada à Universidade
Federal de Viçosa para aprovação no Curso de
Graduação em Engenharia Elétrica sob a
orientação do Prof ° José Tarcísio de Resende.
VIÇOSA
2010
ESTUDO DA ENERGIZAÇÃO, CURTO E DE SITUAÇÕES DE
CARGA QUE OCORREM NA LINHA DE TRANSMISSÃO
JAGUARA-TAQUARIL.
Thiago Cornélio da Fonseca
Aprovada em ____/____/_____.
BANCA EXAMINADORA
_________________________________________________
José Tarcísio de Resende
Ds - Universidade Federal de Viçosa
__________________________________________________
José Carlos da Costa Campos
Ds - Universidade Federal de Viçosa
__________________________________________________
André Gomes Torres
Ds- Universidade Federal de Viçosa
CONCEITO FINAL: ___________________
AGRADECIMENTOS
A Jesus Cristo, amigo sempre presente, sem o qual nada teria feito. Aos meus colegas de
classe e demais formandos pela amizade e companheirismo que recebi. Ao Professor José
Tarcísio de Resende que me acompanhou, transmitindo-me tranqüilidade neste presente
trabalho e ao professor José Carlos da Costa Campos pela ajuda que recebi.
5
RESUMO
Primeiramente será abordado os comportamentos transitórios da simulação da
energização da linha da LT em vazio. Em seguida será feita a análise das situações de faltas
que podem ocorrer nas linhas de transmissão, sejam elas simétricas (trifásica), ou
assimétricas, destacando as faltas fase-fase, bifásica para a terra e fase-terra. Por último
neste trabalho, será estudado a LT para diferentes comprimentos variando de 150 km até
900 km com nível de tensão de 345 KV, variando seu nível de compensação reativa em
derivação de 40 % até 100 % e para as linhas mais longas compensando também 50 % da
sua impedância longitudinal. Este trabalho tem por finalidade estudar a linha de
transmissão, que interliga as subestações de Jaguara - Taquaril, fazendo um comparativo
com o programa de simulação de transitórios eletromagnéticos em redes polifásicas que é
muito utilizado pelas concessionárias de energia elétrica em suas simulações.Será
enfatizado também alguns gráficos ilustrativos e conclusivos acerca do conteúdo do
trabalho desenvolvido. O trabalho encerrará portanto, com algumas interpretações e
conclusões de forma bem sucinta do desempenho de linhas de transmissão.
Palavras-chave: linhas de transmissão, energização, reatores, faltas,
capacitores.
6
LISTA DE ABREVIATURAS E SIGLAS (OPCIONAL)
LT – Linha de transmissão
ONS- Operador nacional do sistema
SIN – Sistema interligado nacional
ATP - Alternative Transients Program
FURNAS – Furnas Centrais Elétricas S.A
RMG – Raio Médio Geométrico
ASCR - Aluminium Conductor Steel Reinforced
AT – Alta tensão
AC – Alternate Current / Corrente Alternada
ATPDraw – Programa Gráfico de Análise de transitórios
EHV – Extra Alta Tensão
TNA – Análise Transitório de Redes
D.B – Diagrama de Blocos
EMTP - Eletromagnetic Transients Program
7
ÍNDICE DE FIGURAS
01-Sistema brasileiro de transmissão de energia elétrica
14
02-Linhas de transmissão de energia elétrica
15
03-Linha utilizada como exemplo neste trabalho
16
04-Torre de transmissão de energia elétrica
17
05-Aplicativo responsável pelo cálculo dos parâmetros.
19
06-Características básicas da LT
22
07-Isoladores utilizados em LT
25
08- Circuito π demonstrativo
26
09-Temperatura em função da Resistência
27
10-Espaçamento simétrico entre os condutores
27
11-Transposição da linha de transmissão
29
12-Disposição eqüidistantes dos condutores
31
13-Método das imagens para cálculo de capacitâncias em LT
35
14-Circuito pi equivalente de uma LT
42
15-Gráfico de várias situações de carga de uma linha
43
16-Sistema simplificado equivalente usado para os testes
59
17- Modelo π usado para simulações de chaveamento
60
8
18-Superposição das ondas de corrente Fase_A
61
19-Superposição das ondas de tensão de entrada da Fase_A
61
20-Superposição das ondas de tensão de saída da Fase_A
62
21-Superposição das ondas de corrente Fase_B
62
22-Superposição das ondas de tensão de entrada Fase_B
63
23-Superposição das ondas de tensão de saída Fase_B
63
24-Superposição das ondas de corrente Fase_C
64
25-Superposição das ondas de tensão de entrada Fase_C
64
26-Superposição das ondas de tensão de saída Fase_C
65
27-Curto circuito (FASE C ) – Tensão na fase A, terminal inicial
66
28-Curto circuito (FASE C ) – Tensão na fase B , terminal inicial.
67
29-Curto circuito (FASE C ) – Tensão na fase C , terminal inicial.
67
30- Curto circuito (FASE C ) – Tensão na fase A , terminal final.
68
31- Curto circuito (FASE C ) – Tensão na fase B , terminal final.
68
32- Curto circuito (FASE C ) – Tensão na fase C , terminal final.
69
33- Curto circuito (FASE AC) – Tensão na fase A, terminal inicial.
70
34- Curto circuito (FASE AC) – Tensão na fase B ,terminal inicial.
70
9
35- Curto circuito (FASE AC) – Tensão na fase C, terminal inicial.
71
36- Curto circuito (FASE AC) – Tensão na fase A , terminal final
71
37- Curto circuito (FASE AC) – Tensão na fase B , terminal final.
72
38- Curto circuito (FASE AC) – Tensão na fase C , terminal final.
72
39- Curto circuito Trifásico, Tensão na fase A, terminal inicial.
73
40- Curto circuito Trifásico, Tensão na fase B, terminal inicial.
73
41- Curto circuito Trifásico, Tensão na fase C, terminal inicial.
74
42- Curto circuito Trifásico, Tensão na fase A, terminal final.
74
43- Curto circuito Trifásico, Tensão na fase B, terminal final.
75
44- Curto circuito Trifásico, Tensão na fase C, terminal final.
75
45- Perfil de tensão ao longo da linha de transmissão
77
46- D.B para obtenção do ganho de tensão sem compensação
78
47- D.B para obtenção do ganho de tensão com compensação
78
48- Tensão a vazio na linha para Linha de comprimento até 900 Km
79
49- Desenho esquemático para simulação Linha 345 KV
80
50- Compensação em série e paralelo L.T
80
51- Diagrama de blocos para obtenção do Reativo
82
10
SUMÁRIO
Página
1- Introdução .........................................................................................12
1.1- Estrutura dos tópicos apresentados no texto ...................................13
1.2- Localização da linha de transmissão utilizada como exemplo ........14
1.3- Descrição da linha de transmissão utilizada como exemplo ...........16
2 – Revisão Bibliográfica .......................................................................21
3- Simulação comparativa com a linha real. ........................................58
3.1- Análise da energização da linha em vazio .......................................59
3.2- Análise dos vários tipos de curto circuitos ......................................66
3.3-Análise das várias situações de carga ..............................................76
4- Resultados e discussões ....................................................................83
5- Referências Bibliográficas .................................................................85
11
1- INTRODUÇÃO
Em virtude do esgotamento das reservas hídricas próximas aos grandes centros
consumidores, é cada vez mais freqüente a construção de usinas geradoras de energia
elétrica distantes desses centros consumidores. Tal condição resulta no transporte de
grandes blocos de energia por longas distâncias. Para reduzir o custo dessa energia e para
efetivamente tornar viável o seu transporte ao longo de distâncias da ordem de 1000 km, é
necessário reduzir o custo das linhas de transmissão, que sem dúvida têm uma parcela
significativa no investimento para expansão do Sistema Interligado de Energia Elétrica
Brasileiro. Atualmente, as decisões para instalar novas unidades geradoras de energia
elétrica estão se tornando complicadas em muitas partes do mundo, devido às dificuldades
em localizar novos locais de implantação dessas unidades, e nenhum tipo de facilidade para
a implantação do sistema de transmissão de energia elétrica.
Há na literatura apenas um caso relatado no Brasil de simulação em uma linha de
transmissão real: Jaguara – Taquaril, pertencente ao sistema Furnas, no estado de Minas
Gerais. Os modelos de linhas de transmissão de energia elétrica podem ser desenvolvidos
no domínio do tempo ou no domínio da freqüência, sendo que a mesma é mais facilmente
representada no domínio da freqüência. No entanto o sistema elétrico, no qual as linhas de
transmissão estão inseridas, possui diversos elementos não lineares que são de difícil
representação no domínio da freqüência. Deste modo dá-se preferência por modelos de
linha que são desenvolvidos diretamente no domínio do tempo. Um dos primeiros modelos
a representar a linha de transmissão diretamente no domínio do tempo foi desenvolvido por
H. W. Dommel e baseou-se no método das características ou método de Bergeron e
consiste em combinar o método das características com o método numérico de integração
trapezoidal, resultando em um algoritmo que é capaz de simular transitórios
eletromagnéticos em redes cujos parâmetros são discretos ou distribuídos (Dommel,
1969).Este algoritmo sofreu sucessivas evoluções e atualmente é conhecido como
Eletromagnetic Transients Program, ou simplesmente EMTP (Dommel, 1986).}. Em nosso
estudo, o enfoque está voltado para os circuitos π e para o modelo de parâmetros
distribuídos, no domínio do tempo.
12
1.1 – Estrutura dos tópicos apresentados no texto
Na seqüência deste capítulo, a descrição do sistema elétrico de transmissão do
estado de Minas Gerais é apresentada. No caso, é em Minas Gerais que se localiza a linha
de transmissão que foi utilizada para aplicação da modelagem matemática apresentada
neste trabalho. Nos tópicos a seguir, será mostrado a linha em estudo com suas
características elétricas e mecânicas, bem como seus parâmetros elétricos necessários para
a simulação computacional. Foi feito uma abordagem geral das linhas de transmissão,
listando os efeitos que as diversas cargas ocasionam na LT. Apresentamos também as
diversas faltas que ocorrem nas LTs, bem como os efeitos existentes na mesma como,
efeito Ferranti, efeito corona e efeito skin ou pelicular. E por fim, após as conclusões, são
apresentadas as referências bibliográficas nas quais este trabalho foi baseado.
13
1.2 - Localização da linha de transmissão utilizada como exemplo
A figura 1 mostra um esquema do sistema brasileiro de transmissão de energia
elétrica. A figura 2 mostra as linhas de transmissão pertencente ao sistema do estado de
Minas Gerais. Essas figuras foram obtidas na página do Operador Nacional do Sistema
(ONS).
Figura 1 – Sistema brasileiro de transmissão de energia elétrica
14
Figura 2 – linhas de transmissão de energia elétrica
Esta linha é a que interliga as subestações de Jaguara a Taquaril, com uma extensão
de aproximadamente 400 km, pertencente ao sistema Furnas, cuja figura representativa
acima foi obtida do site da (ONS), que é o operador do sistema elétrico brasileiro, que
detém o controle, operação e despacho da energia elétrica.
15
1.3 – Descrição da linha de transmissão utilizada como exemplo.
É uma linha pertencente ao sistema FURNAS, localizada no estado de Minas Gerais
e utilizada no desenvolvimento dos primeiros protótipos dos programas do tipo EMTP,
software mais empregado hoje em dia pelos profissionais do ramo. Essa linha interliga as
subestações de Jaguara e Taquaril. Como essa linha serviu de base para o desenvolvimento
dos principais programas de simulação de transitórios em redes elétricas, as comparações
feitas neste trabalho têm o objetivo de mostrar que a modelagem proposta através de
simulações feitas no computador é adequada às principais ferramentas para esse tipo de
aplicação. A linha não sofre transposição e a resistividade do solo usada na simulação é de
1000 Ω.m. A tensão de serviço original é 345 KV. Um esquema dessa linha é mostrado na
próxima figura. No caso das simulações apresentadas, foi considerado um comprimento de
400 km para a linha esquematizada a seguir.
Figura 3 – Linha Jaguara - Taquaril localizada em Minas Gerais (FURNAS).
16
Figura 4 – Torre da linha transmissão do sistema 345 KV Furnas
17
1.3.1 – Dados elétricos da linha de transmissão 345 KV
Para este sistema, tomamos como referência à configuração da torre de 345 kV da
linha Jaguara - Taquaril, onde os condutores de fase estão em feixe duplo com 2 x 954
MCM - ACSR. Os cabos pára-raios são feitos de aço galvanizado EHS’’, aterrados ao
longo da linha. A resistividade do solo assumida é 1000 Ω.m.
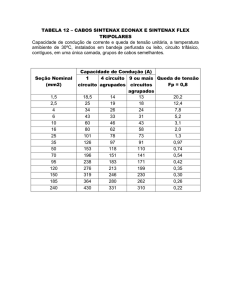
Tabela1 - Características dos cabos condutores do sistema de 345 KV
Dados dos cabos da linha de 345 KV
Condutores de fase tipo: Rail
N° de condutores em feixe
2
Distância dos feixes em (m)
0.2
Diâmetro do condutor externo (m)
0.0281432
Diâmetro do condutor interno (m)
0.00739
Resistência a 60 Hz em (Ω/km )
0.0800497
Temperatura °C
45
Permeabilidade magnética relativa
1
Permissividade relativa
1
Flecha a meio vão (m)
14.6
Tabela 2 - Características do cabo pára-raios no sistema de 345 kV.
Cabo para raios EHS 3/8’’ (sólido)
Resistência a 60 Hz (Ω/km)
4.188
Temperatura °C
45
0,009144
Diâmetro do condutor
Permeabilidade magnética relativa
70
Permissividade magnética
1
Flecha a meio vão (m)
10.62
18
1.3.2 – Parâmetros elétricos
Os parâmetros elétricos obtidos para o sistema de 345 KV (Jaguara - Taquaril) são
mostrados abaixo e foram calculados com base nos dados das características dos cabos
elétricos dispostos anteriormente, através de um programa desenvolvido em ambiente
computacional, através de um software adequando. A potência natural desta linha de
transmissão é de 412,25 MW.
Figura 5 - Aplicativo responsável por calcular os parâmetros da LT
19
Seqüência zero:
Resistência (Ω/km)
Indutância (mH/km)
Capacitância (ηF/km)
0.32183
3.36
8
Seqüência positiva:
Resistência (Ω/km)
Indutância (mH/km)
Capacitância (ηF/km)
0.03419
0.9943
11.8
Para conhecer o grau de compensação adequado para reduzir o efeito Ferranti,
devemos calcular o ganho de tensão no final da linha em vazio, que será abordado nos
capítulos procedentes.
20
2- REVISÃO BIBLIOGRÁFICA
O estudo de linhas de transmissão tem grande importância, destacando, entre outras
análises, cálculos de fluxo de carga, determinação de níveis de curto-circuito, modelagem
de fenômenos eletromagnéticos. Na modelagem das linhas de transmissão, há dificuldades
na correta representação das mesmas e na aferição dos modelos utilizados, sendo relatado
apenas um caso no Brasil, realizado na linha Jaguara-Taquaril do sistema Furnas,
localizada no estado de Minas Gerais. Para o fornecimento de energia a centros
consumidores, os sistemas elétricos de potência e, de forma específica, as linhas de
transmissão operam em regime permanente (tensão, corrente e freqüência nominais e
constantes), interligando tais centros consumidores aos centros de geração de energia. No
entanto, o dimensionamento desses sistemas de transmissão deve basear-se na proteção
contra ocorrências transitórias e extremas acima das condições normais de funcionamento.
A linha de transmissão e seus sistemas de proteção e controle são dimensionados em
relação à probabilidade de ocorrência dos fenômenos transitórios. Os simuladores de redes
elétricas são ferramentas utilizadas para isso. Entre os mais conhecidos destacamos o TNA,
que é o analisador transitório de redes.
21
O desempenho elétrico de uma linha de transmissão depende de suas características
físicas.
Os Componentes de uma linha de transmissão são exibidos na figura 06:
(1) condutores
(2) isoladores (cadeia de isoladores de porcelana ou vidro)
(3) estruturas de suporte (torres, postes)
(4) cabos pára-raios (cabos de aço colocados no topo da estrutura para proteção
contra raios)
Figura 06 – Características básicas da LT
Classes de tensão que temos disponíveis no Brasil:
Sigla
Denominação
LV
low voltage
MV
medium voltage
HV
high voltage
EHV
extra high voltage
UHV
ultra high voltage
Valores típicos de tensão (de linha)
< 600 V
13,8 23 34,5 69 KV
115 138 230 KV
345 440 500 600DC 765 KV
1100 KV
22
Os condutores constituem os elementos ativos das linhas de transmissão. Devem
possuir as características: alta condutibilidade elétrica, baixo custo, boa resistência
mecânica, baixo peso específico e alta resistência a oxidação e à corrosão por agentes
químicos poluentes. Atualmente são usados cabos de alumínio em vez do cabo de cobre
pois, são mais barato, mais leve, requer área da seção reta maior que o cobre para as
mesmas perdas, melhor desempenho em face ao efeito corona(diâmetro maior) e o custo é
em torno de 25% do cobre. A padronização de cabos no Brasil segue a norma norte
americana AWG. Entre as unidades mais comumente usadas, destacamos :
Comprimento: metro [m], pé (foot) [ft], milha (mile) [mi]
1 ft = 0,3048 m, 1 in = 0,025376 m
1 mi = 1609 m
A área da seção reta: milímetro quadrado [mm2], circular mil [CM](*)
(*) 1 CM = corresponde a área
de um círculo de um milésimo de polegada
(mil) de diâmetro.
O encordoamento normal dos cabos condutores, quando compostos de fios de
mesmos diâmetros, obedece a equação:
N = 3.x²+ 3.x +1
(2.1)
onde,
N - número total de fios componentes;
X - número de camadas e coroas
A linha utilizada em nosso trabalho especificamente emprega cabos ASCR
(alumínio com alma de aço): aço mais barato que alumínio, a alma de aço o faz ser mais
resistente à tração (admite lances maiores), isto faz com que este cabo seja o mais usado
para níveis de tensão elevados.
Os isoladores, além de adquirirem o isolamento elétrico, devem suportar os cabos e
às diversas solicitações mecânicas que estão sujeitas:
23
- Forças verticais;
- Forças horizontais axiais;
- Forças horizontais transversais;
Solicitações de natureza elétrica:
- Tensão normal e sobretensões em frequência industrial;
- Surtos de sobretensões de manobra (podendo atingir 3 a 5 vezes a tensão nomal);
- Sobretensões de origem atmosférica ( com intensidades variadas podendo ser de
grandes valores);
Material utilizado:
- Porcelana vitrificada;
- Vidro temperado;
Os isoladores tipo suspensão, monocarpo e de disco são os mais utilizados para as
tensões de 345 KV.
Os cabos pára-raios ocupam a parte superior das estruturas e se destinam a
interceptar descargas de origem atmosférica e descarregá-las para o solo, evitando que
causem danos e interrupções nos sistemas.
Os cabos mais utilizados são os de (3/8’’ a ½’’):
- cabos de aço HS, HSS ou SM galvanizados;
- cabos aluminoweld;
- Cabos copperweld;
- cabos CAA, de alta resistência mecânica;
24
Parâmetros da Linha de Transmissão
Figura 07- Isoladores utilizados em LT
→ Resistência (R)
Dissipação de potência ativa devido à passagem de corrente;
→ Condutância (G)
Representação de correntes de fuga entre condutores e nos isoladores (principal
fonte de condutância);
Depende das condições de operação da linha (umidade relativa do ar, nível de
poluição, etc.). É muito variável, em função dos fatores acima.Seu efeito é em geral
desprezado (sua contribuição no comportamento geral de operação da linha é muito
pequena);
→ Indutância (L)
Deve-se aos campos magnéticos criados pela passagem das correntes;
→ Capacitância (C)
Deve-se aos campos elétricos: carga nos condutores por unidade de diferença de
potencial entre eles.Com base nessas grandezas que representam fenômenos físicos que
ocorrem na operação das linhas, pode-se obter um circuito equivalente (modelo) para a
mesma, como por exemplo:
25
Figura 08- Circuito π demonstrativo
Resistência (R)
Causa a dissipação de potência ativa:
R=
potênciadissipada
I 2 ef
(2.2)
Resistência CC:
R0 = ρ
l
(Ω)
A
(2.3)
0nde,
ρ - resistividade do material (Ω.m)
L – comprimento (m)
A – área da seção reta (m2)
Cobre recozido a 200c - ρ = 1,77x10-8 Ω.m
Alumínio a 200c - ρ = 2,83x10-8 Ω.m
ρ depende da temperatura → Ro varia com a temperatura (ρ aumenta → Ro
aumenta
R2 T + t 2
=
R1 T + t1
(2.4)
Em que T depende do material,sendo T = 234, 5 cobre recozido com 100% de
condutividade, T = 241 cobre têmpera dura com 97,3% de condutividade, T = 228
alumínio têmpera dura com 61% de condutividade
26
Figura 09-Gráfico Temperatura em função da Resistência
Ro aumenta de 1 a 2% para cabos torcidos (fios de alumínio torcidos, p.ex, cabos
ACSR)
Para se ter “x” metros de cabo, necessita-se de 1,01 x a 1,02 x metros de fios para
depois agrupá-los e torcê-los. Em corrente alternada a distribuição de corrente não é
uniforme pela seção reta do condutor → a corrente concentra-se na periferia do condutor.
Área útil para passagem da corrente diminui → RAC > Ro → efeito pelicular (skin
affect).
Equações da indutância de um linha trifásica com espaçamento simétrico:
Figura 10 - Espaçamento simétrico entre os condutores
Da figura podemos tirar que:
Os três condutores tem raios iguais, portanto o mesmo RMG, igual a Ds;
a distância entre condutores é D.Não há fio neutro ou o circuito é equilibrado → Ia
+ Ib + Ic = 0.Fluxo concatenado com o condutor da fase a (há contribuições das três
correntes):
27

λa = 2.10 −7  I a ln


= 2.10 −7  I a ln


= 2.10 −7  I a ln

1
1
1
+ I b ln + I c ln 
DS
D
D

1
1
1
1
+ ( I b + I c ) ln  = 2.10 −7  I a ln
− I a ln 
DS
D
DS
D



1
D
+ I a ln D  = 2.10 −7  I a ln
DS
DS



 (Wb/m) (2.5)

Indutância da fase a:
La =
λa
Ia
= 2.10 −7 ln
D
DS
(H/m)
(2.6)
Por simetria, para as outras fases tem-se La = Lb = Lc
Portanto,
La = Lb = Lc = 2.10 −7. ln
D
(H/m)
DS
(2.7)
Equações da indutância para uma linha trifásica com espaçamento assimétrico:
O fluxo concatenado e a indutância de cada fase são diferentes → circuito
desequilibrado;
Equilíbrio é obtido através da transposição:
28
Figura 11 – Transposição da linha de transmissão
Cálculos considerando a transposição são mais simples.Linhas não transpostas →
considera-se a linha como transposta e a sua indutância como a média das indutâncias das
fases.Fluxo concatenado com fase a, primeiro trecho:

λa1 = 2.10 −7. I a ln

1
1
1 

+ I b ln
+ I c ln
DS
D12
D31 
(2.8)
Fluxo concatenado com fase a, segundo trecho:

λa 2 = 2.10 −7. I a ln

1
1
1 

+ I b ln
+ I c ln
DS
D23
D12 
(2.9)
Fluxo concatenado com fase a, terceiro trecho:
29

λa3 = 2.10 −7. I a ln

1
1
1 

+ I b ln
+ I c ln
DS
D31
D23 
(2.10)
Fluxo médio concatenado com a fase a:
λa =
λa1 + λa 2 + λa 3
3
=

2.10 −7 
1
1
1

. 3.I a ln
=
+ I b ln
+ I c ln
3 
DS
D12 D23 D31
D12 D23 D31 

2.10 −7 
1
1

. 3.I a ln
− I a ln
3 
DS
D12 D23 D31 
= 2.10 −7.I a . ln 3
D12 D23 D31
(Wb/m)
DS
(2.11)
Indutância média por fase da linha trifásica com transposição:
La = 2.10 −7 . ln
Em que,
Deq = 3 D12 D23 D31
Deq
DS
(H/m)
(2.12)
, é o espaçamento eqüilátero equivalente da linha
30
Equações da capacitância de Linhas Trifásicas com Espaçamento Simétrico
Considere a seguinte linha de transmissão trifásica:
Figura 12 – Disposição equidistantes dos condutores
Considere a situação mais comum na prática:
condutores idênticos: ra = rb = rc = r;
linha equilibrada: qa + qb + qc = 0;
Tensões fase-fase → cada tensão recebe contribuição das três cargas:
Vab =
1 
D
r
D
 q a ln + qb ln + qc ln 
2.π .ε o 
r
D
D
(2.13)
Vbc =
1
2.π .ε o
D
r

 qb ln + qc ln 
r
D

(2.14)
Vca =
1 
r
D
 q a ln + qc ln 
2.π .ε o 
D
r
(2.15)
Considere os fasores de tensão:
31
Van = V .∠0 0 ; Vbn = V .∠ − 120 0 ; Vcn = V .∠120 0 (V)
(2.16)
Vab = 3.V .∠30 0 ; Vbc = 3.V .∠ − 90 0 ; Vca = 3.V .∠150 0 (V)
(2.17)
Pode-se mostrar que:
Van =
1
(Vab − Vca )
3
(2.18)
Fazendo as substituições:
1
1 
D
r
r
D
Van = .
 q a ln + qb ln − q a ln − q c ln 
3 2.π .ε o 
r
D
D
r
(2.19)
Considerando qc = -(qa + qb):
3
qa
qa
D
D
Van =
ln  =
ln 
6.π .ε o  r 
2.π .ε o  r  (V)
(2.20)
A capacitância fase-neutro vale:
C an =
qa
2.π .ε o
=
(F/m)
Van
D
ln 
r
(2.21)
Equações da capacitância de Linhas Trifásicas com Espaçamento Assimétrico
Considere a seguinte linha trifásica:
Hipóteses:
32
Os condutores tem o mesmo raio r, linha é transposta (igual ao caso da indutância)
→ obtém-se a capacitância média;
Considerando a transposição, a linha pode ser separada em três trechos distintos:
Para o trecho 1 em que a fase a está na posição 1, b na posição 2 e c na posição 3,
tem-se:
Vab1 =
1
2.π .ε o

D 
D
r
 q a ln 12 + qb ln
+ qc ln 23 
r
D12
D31 

(2.22)
Analogamente para os outros 2 trechos:
Vab2 =
1
2.π .ε o

D
D 
r
 q a ln 23 + qb ln
+ qc ln 31 
r
D23
D12 

(2.23)
Vab3 =
1
2.π .ε o

D
D 
r
 q a ln 31 + qb ln
+ qc ln 12 
r
D31
D23 

(2.24)
A tensão Vab é a média das tensões nos três trechos:
33
Vab =
3 D D D

r
12 23 31
 q a ln
+ qb ln

3 D D D
r
12 23 31





(2.25)
3 D D D

r
12 23 31
 q a ln
+ q c ln

3 D D D
r
12 23 31





(2.26)
1
1
Vab1 + Vab2 + Vab3 =
3
2.π .ε o
(
)
Analogamente:
Vca =
1
1
Vca1 + Vca2 + Vca3 =
3
2.π .ε o
(
)
Lembrando que:
Vab =
1
Vab − Vca
3 1
(
)
(2.27)
qa
(2.28)
Van
tem-se naturalmente (para carga equilibrada → qa + qb + qc = 0:
e
C an =
C an = C bn = C cn =
Em que Deq. =
3
D12 D23 D31
2.π .ε o
Deq
ln(
)
r
(F/m)
(2.29)
é o espaçamento eqüilátero da linha.
34
Efeito do Solo sobre a Capacitância de Linhas Trifásicas
Utiliza-se o método das imagens:
Figura 13- Método das imagens para cálculo de capacitâncias em LT
Obtém-se uma expressão para a capacitância que leva em conta as distâncias entre
os condutores e as distâncias entre os condutores e as imagens:
2.π .ε o
C an =
ln(
Deq.
r
.
3
3
H 1 .H 2 H 3
H 12 .H 23 .H 31
(F/m)
(2.30)
)
35
- Condutores Múltiplos por Fase
Para n condutores, considera-se que a carga em cada um seja de qa/n (para a fase a);
O procedimento para a obtenção da capacitância é semelhante ao que já foi feito
até agora e o resultado final é:
C an =
2.π .ε o
 Deq.
ln b
 D aC



(F/m)
(2.31)
em que:
D b aC = r.d
(2.32) dois condutores por fase (cálculo utilizado para a
linha Jaguara-Taquaril).
D b aC = 3 r.d 2
(2.33) três condutores por fase
D b aC = 1,09.4 r.d 3
(2.34) quatro condutores por fase
b
Os D aC são RMG modificados em relação aos RMG usados no cálculo das
indutâncias, pois o raio externo substitui o raio efetivo.
36
Equação geral da Linha de Transmissão
Modelo para linhas longas
37
A corrente pela impedância série é a média das correntes no início e no meio do
trecho diferencial:
I +( I + ∆I )
∆I
=I+
2
2
(2.36)
A tensão na admitância shunt é a media das tensões no início e no meio do trecho
diferencial:
V +(V + ∆V )
∆V
=V +
2
2
(2.37)
As tensões no início e no fim do trecho diferencial são V e V +∆V ,
respectivamente. A diferença ∆V se deve à queda de tensão associada à passagem de
corrente (média) pelos parâmetros série:
V + ∆V = V − z∆x Im medio
∆V = −( z∆x).( I +
(2.38)
∆I
z∆x∆I
) = − zI∆x −
≈ − zI∆x
2
2
(2.39)
As correntes no início e no fim do trecho diferencial são I e I + ∆I, respectivamente.
A diferença ∆I se deve ao desvio de parte da corrente pelos parâmetros shunt, que estão
submetidos a uma tensão (média):
I + ∆I = I − y∆xVmmedio
∆I = −( y∆x).(V +
(2.40)
y∆x∆V
∆V
) = − yV∆x −
≈ − yV∆x
2
2
(2.41)
Note que os produtos de termos diferenciais são desprezados (muito pequenos)
Fazendo ∆x → 0 (definição de derivada):
38
d
V = − zI
dx
(2.42)
d
I = − yV
dx
(2.43)
- Derivando em relação a x:
d²
d
V = −z I
dx ²
dx
(2.44)
d²
d
I = −y V
dx ²
dx
(2.45)
Fazendo as substituições das derivadas:
d²
V = − zyV
dx ²
(2.46)
d²
I = − zyI
dx ²
(2.47)
Que depois de algumas modificações pode ser posta na seguinte forma:
d²
V ( x) = γ ²V ( x)
dx ²
d²
I ( x ) = γ ² I ( x)
dx ²
(2.48)
(2.49)
Resolvendo as equações de onda, temos que :
γ = zy = ( R + jwL)(G + jwC ) = α + jβ
(2.50)
em que γ é a constante de propagação, α é a constante de atenuação e β é a
constante de fase
39
V ( x) = V (l ) cosh(γx) + ZcI (l ) senh(γx)
(2.51)
1
V (l ) senh(γx)
Zc
(2.52)
I ( x) = I (l ) cosh(γx) +
Em que l é o comprimento da linha, V (l) e I (l) corresponde a tensão e a corrente
no final da linha e x é medido a partir do final da linha em direção ao início da linha.
Esta equação acima é a equação geral de uma linha de Transmissão em que Zc, é
a impedância característica da linha → interpretação: Zc é a impedância a ser colocada no
final da linha para que se tenha a máxima transferência de potência entre gerador e carga
→ casamento de impedâncias.
γ = zy
Zc =
z
y
(2.53)
(2.54)
E dependem somente dos parâmetros da linha.
40
Representação da linha de transmissão por quadripolos
A = D = cosh(γl )
(2.55)
B = Zc.senh(γl )
(2.56)
1
senh(γl )
Zc
(2.57)
C=
Os parâmetros ABCD são conhecidos como constantes genéricas do quadripolo
equivalente de uma LT de parâmetros distribuídos. Se o circuito interior do quadripolo é
constituído apenas por elementos passivos, o quadripolo diz-se passivo. Dada às condições
de simetria de uma LT, ou seja, seus terminais podem ser invertidos (entrada → saída e
saída → entrada) sem alterar o comportamento do sistema a que pertence, tem-se que A=D.
Assim, o quadripolo equivalente de uma LT é simétrico e satisfaz à condição:
AD – BC = 1
(2.58)
41
O circuito equivalente π de uma linha de comprimento “l”
Figura 14-Circuito π equivalente de uma LT
Do circuito π equivalente tem se que :
Y1 = Y2 =
1
γl
tanh( )
Zc
2
Z = Zcsenh(γl )
(2.59)
(2.60)
A carga SIL corresponde ao carregamento característico da linha, ou seja quando a
impedância da carga é equivalente a impedância de surto.
Em geral é utilizada a tensão nominal para o cálculo da SIL. Ela fornece um termo
de comparação das capacidades de carregamento da linha.
SIL =
V ² no min al
L
C
(2.61)
A linha de transmissão está submetida à varias situações de carga, como por
exemplo: carga leve , carga pesada , carga nominal, carga SIL e o caso de um curto circuito
42
nos terminais da linha. O gráfico abaixo exemplifica esta situação em função da tensão e do
comprimento da linha.
Figura 15 – Gráfico de várias situações de carga de uma linha.
43
FALTAS EM LINHAS DE TRANSMISSÃO
A ocorrência de uma situação inesperada em um sistema de transmissão de energia
elétrica pode causar a interrupção no fornecimento de energia. Esta ocorrência aleatória e
imprevisível, na maioria das vezes, é conhecida como falta. A interrupção do fornecimento
é realizada por equipamentos de proteção, visando resguardar a estabilidade do sistema e os
equipamentos envolvidos na transmissão da energia. O rápido restabelecimento do
fornecimento de energia depende da localização do ponto onde ocorreu a falta no sistema e
a realização dos reparos necessários. As linhas de transmissão de energia elétrica compõem
a maior parte, em extensão, do sistema de transmissão de energia. Devido a este fato, a
maioria das faltas que ocorrem no sistema elétrico de potência, envolvem as linhas de
transmissão. As faltas em linhas de transmissão podem ocorrer,
devido a diversos
fatores,tais como: problemas na isolação, “queimadas”próximas a linha de transmissão,
contatos entre os cabos da linha de transmissão (devido ao envolvimento de agentes
externos), entre outros. As linhas de transmissão trifásicas compõem a maior parte do
sistema de transmissão de energia no Brasil e a maioria das faltas que ocorrem nestas
linhas de transmissão são as que envolvem o contato de uma das fases com a terra (faseterra) com 70 % de incidência. A seguir serão demonstradas matematicamente as faltas
que ocorrem no sistema de transmissão de energia, bem como seus diagramas de ligação
para cada situação de falta.
44
Para se estudar curto circuito é importante conhecer sobre o método das
componentes simétricas (também conhecido como Teorema de Fortescue). Esse método, é
importante para o estudo de sistemas elétricos de potência polifásicos desequilibrados.
Consiste na decomposição dos elementos de tensão ou corrente das fases, em parcelas
iguais, mas com ângulos diferentes. Desta forma é possível desmembrar o circuito
polifásico desequilibrado em ‘n’ circuitos monofásicos, supondo válido o princípio da
superposição, ou seja, que os circuitos sejam lineares.
No caso do sistema trifásico, haverá três componentes: zero,positiva e negativa. A
componente positiva representa o elemento de tensão ou corrente em condições normais
equilibradas, com um sentido de giro, por convenção, positivo. A componente de seqüência
negativa representa o elemento de tensão ou corrente com sentido de giro inverso. A
componente de seqüência zero ou homopolar representa e elemento de tensão ou corrente
não girante. Por exemplo, um vetor de tensões de fase pode ser expresso por:
Com o equivalente em componentes simétricas, temos:
A relação entre as tensões é definido por:
45
Onde
, representa a defasagem de 120° entre as tensões.
A matriz de transformação(ou também chamada matriz de Fortescue)
será definida por:
Falta Fase-Terra
Possui grau de incidência: 70%
G
a
b
c
Sistema
Zo, Z1, Z2
~
Zf Impedância
falta-terra
ZO, Z1, Z2: impedâncias do sistema, visto a partir do ponto de defeito;
Ea, Eb, Ec: tensões equivalentes – f.e.m. de seq. Positiva.
Condições no ponto de falta:
Va = ZfIa
Ib = Ic = 0
(2.62)
(2.63)
46
desprezam-se as correntes de carga.
a1) Correntes:
1 1 1 
Ia0 
I a 

 I  = 1 1 a a 2  0 
 a1 
3
 
 Ia2 
 0 

2
a
a
1


1
I a 0 = I a1 = I a 2 = I a
3
(2.64)
a2) Tensões:

Va 0  0   Z 0
V  =  E  − 0
 a1   1  
Va 2  0  0


Va 0 = − Z 0
0
Z1
0
1
Ia
3
Va1 = E1 − Z 1
Va 2 = − Z 2
Retomando
1
Ia
3
1
Ia
3

0  I 
a
1  
0
Ia
3 
Z 2   Ia 

(2.65)
(2.66)
(2.67)
Va = ZfIa
− Z 0 Ia
− Z 0 Ia − Z 0 Ia
+ E1
+
Va
3
3
3
Ia =
=
Zf
Zf
(2.68)
Tirando Ia:
47
Ia =
3E1
Z 0 + Z 1 + Z 2 + 3Z f
(2.69)
As componentes de corrente serão:
E1
Ia
= I ao = I a1 = I a 2 =
3
Z 0 + Z 1 + Z 2 + 3Z f
(2.70)
Diagrama esquemático de ligação:
seq. +
seq. -
seq. 0
Va2
Va0
Z0’
Z1
Va1
Z2
Ia1
Ia2
Z0
3Zn
E1
Ia0
~
N1
3Zf
Ia1
Ia2
componentes
da
corrente C.C.
Ic1
Ib1
Ib2
Ic2
Ia0 Ib0 Ic0
48
Falta entre duas FASES
Possui grau de incidência: 15%
G
a
b
c
Sistema
Zo, Z1, Z2
~
Zf
a) Condições no ponto de falta:
Vb − Vc = Z f Ib
(2.71)
Ia = 0
(2.72)
Ib = − Ic
(2.73)
a1) Componentes simétricos da corrente:
1 1 1 
Ia0 

 0 
 I  = 1 1 a a 2  − I 
 a1 
3
 c 
 Ia2 

  I c 
2
1
a
a


I a0 = 0
(2.74)
∴ I b0 = I c0 = 0
(2.75)
I a 2 = − I a1
(2.76)
a2) Componentes simétricos das tensões:

Va 0  0   Z 0
V  =  E  − 0
 a1   a1  
Va 2  0  0


0
Z1
0

0  I 
ao
 
0  I a1
 
Z 2   I a 2 

49
Va 0 = − Z 0 I a 0 = 0
(2.77)
Va1 = Ea1 − Z1 I a1
(2.78)
Va 2 = Z 2 I a1
(2.79)
Vb2 = Z 2 I b1
(2.80)
Vc 2 = Z 2 I c1
(2.81)
Vb0 = −Z 0 I b0 = 0
(2.82)
Vb1 = Eb1 − Z1 I b1
(2.83)
Vc0 = −Z 0 I c0 = 0
(2.84)
Vc1 = Ec1 − Z1 I c1
(2.85)
Usando expressões análogas para Vb e Vc e partindo de
Vb − Vc = Z f Ib ,
chegamos a:
Vb = Vb0 + Vb1 + Vb2
(2.86)
Vc = Vc0 + Vc1 + Vc2
(2.87)
Ib = Ib0 + Ib1 + Ib2 = 0
(2.88)
Ia0 = 0
(2.89)
50
(2.90)
− Ia1 = Ia2
Ia1 =
Ea1
z f + z1 + z2
(2.91)
I f = Ib = Ib0 + Ib1+ Ib2 = α ² Ia1 + αIa2
(2.92)
I f = α ² Ia1 − αIa1 = (α ² − α ) Ia1
(2.93)
(α ² − α )1 = − j 3
Corrente de Falta será:
If = − j
(2.94)
3Ea1
z f + z1 + z2
(2.95)
Circuito equivalente: o circuito de seqüência 0 (zero) não é utilizado (não haverá
circulação de corrente de neutro no gerador).
Ia1
Ia1
Ia2
Va1
Ic2
Ib2
Z1
Z2
Ea
Va2
Ic1
Zf
Ib1
Ia2
Componentes corrente C.C.
Ia0 = Ib0 = Ic0 = 0
51
Falta entre duas FASES e terra
Possui grau de incidência: 10%
G
a
b
c
Sistema
Zo, Z1, Z2
~
Zf
a)Condições no ponto de falta:
Ia = 0
Vb = Vc = Z f I f
Ib + Ic = I f
(2.96)
(2.97)
(2.98)
a1) Componentes simétricos da tensão
1 1 1 
Va 0 

 Va 
V  = 1 1 a a 2  V 
 a1 
3
 b 
Va2 

 Vb 
2
1
a
a


V a1 = E a1 − I a1 Z 1
(2.99)
Va 2 = 0 − I a 2 Z 2
(2.100)
Va 0 = 0 − I a 0 Z 0
(2.101)
a2) Componentes simétricos das correntes
52
Partindo de Vb = Vc =
I a1 =
I a2 = −
IfZf
Z 0 + Z 2 + 3Z f
Z 1 Z 2 + ( Z 0 + 3Z f )( Z 1 + Z 2 )
Z 0 + 3Z f
Z 1 Z 2 + ( Z 0 + 3Z f )( Z 1 + Z 2 )
I f = 3I a 0
I a0 =
e fazendo algumas substituições, chegamos a:
E a1
E a1
(2.102)
(2.103)
(2.104)
− Z2
E a1
Z 1 Z 2 + ( Z 0 + 3Z f )( Z 1 + Z 2 )
(2.105)
A interligação dos circuitos para os vários tipos de faltas são mostradas a seguir.
53
LIGAÇÕES DOS CIRCUITOS PARA OS VÁRIOS TIPOS DE FALTAS
Falta trifásica
Seq. +
P
Ia
Zf
Falta entre duas FASES
Seq. +
P
Va1
Seq. -
P
Va2
Zf
Ia1 = -Ia2
54
Falta linha-terra
Seq. +
Va1
P
Ia1
Seq. -
Va2
P
IG1
Ia2
Seq. 0
Va0
P
Ia0
3Zf
Falta entre duas
linhas-terra
Seq. +
P
Va1
Seq. -
P
Seq. 0
P
Va0
Ia1
Ia2
Va2
Ia0
3Zf
55
Compensação das Linhas de Transmissão
Para linhas com grandes comprimentos, acima de 400 km, como é o caso da linha
em estudo é necessário o uso de equipamentos de compensação, tais como reatores e
capacitores em paralelo e capacitores em série, para aumentar a capacidade da linha.
Os reatores em paralelo (também chamados de reatores shunt) anulam parcialmente
o efeito capacitivo da linha, minimizando o Efeito Ferranti, que ocorre quando a linha
opera em carga leve. Estes reatores geralmente não são manobráveis, o que pode ser
indesejável quando a linha estiver em sobrecarga.A manobra convencional de um reator
pode levar a sobretensões indesejáveis, e é evitada na medida do possível. O uso de
reatores controláveis permite uma maior flexibilidade, mas acrescenta uma maior
complexidade e custo no sistema de transmissão.
As linhas CA de Itaipu foram as primeiras a usar o sistema de compensação em
série, por se tratar das longas distâncias de suas linhas de transmissão.
A compensação série é um recurso muito utilizado para aumentar a capacidade de
transmissão de energia das linhas de transmissão. Somente no Sistema Interligado Nacional
(SIN) existem mais de 40 bancos de capacitores série, entre fixos e controlados, todos
instalados nos terminais de suas respectivas linhas de transmissão. Entretanto, a utilização
deste recurso tem um grande impacto na complexidade dos sistemas de proteção.
Dentre os fenômenos relacionados com a compensação série, que afetam a
proteção, podemos destacar os seguintes:
- Inversão de tensão;
- Inversão de corrente;
- Ressonância Subsíncrona;
- Desbalanço das impedâncias de Fase;
56
Efeitos ocorrentes nas linhas de transmissão
Destacaremos os principais efeitos que ocorrem nas LT, que são o efeito corona,
efeito pelicular (Skin Affect) e Efeito Ferranti.
Efeito Corona:
É um fenômeno relativamente comum em linhas de transmissão com sobrecargas.
Devido ao campo elétrico muito intenso nas vizinhanças dos condutores, as partículas de ar
que os envolvem tornam-se ionizadas e, como consequência, emitem luz quando da
recombinação dos íons e dos elétrons. O efeito corona é também conhecido como fogo-desantelmo. Esse nome vem de Santo Elmo, padroeiro dos marinheiros, e surgiu quando
antigos marinheiros observaram navios com os mastros envoltos por uma tênue luz. A
superstição
cuidou
de
transformar
esse
fenômeno
em
aparição
divina.
Posteriormente, porém, observou-se que tal aparição ocorria principalmente em regiões
tropicais, em condições que precediam tempestades. Nuvens eletrizadas induziam cargas
nas pontas dos mastros dos navios, produzindo o efeito corona. O efeito corona
corresponde à ionização da região em torno do condutor. Este efeito aumenta a
“resistência” do condutor, gerando mais perdas (perda por efeito corona) e aumentando o
amortecimento da linha para perturbações transitórias. A capacitância da linha varia
durante a ocorrência do efeito mencionado.
Efeito Pelicular (Skin affect):
O efeito pelicular é o fenômeno responsável pelo aumento da resistência aparente
de um condutor elétrico em função do aumento da frequência da corrente elétrica que o
percorre. Se em corrente contínua, a corrente elétrica se distribui de forma uniforme ao
longo de toda a secção reta do condutor elétrico, já em corrente alternada isso não ocorre.
Na realidade, à medida que aumenta a frequência da corrente que percorre o condutor, o
campo magnético junto ao centro do condutor também aumenta conduzindo ao aumento da
reatância local. Este aumento da reatância faz a corrente a se deslocar pela periferia do
condutor, o que implica na diminuição da área efetiva do condutor e logo um aumento da
sua resistência aparente.
57
Efeito Ferranti :
O efeito Ferranti faz com que a tensão aumente ao longo da linha de transmissão.
Na ausência de compensação reativa, a tensão de regime no final da linha de transmissão é
sempre maior do que no início dependendo da situação da carga, principalmente em vazio,
a tensão no extremo da linha, pode chegar a valores exorbitantes.
Para melhor visualização, considere a equação global da LT, em que I(l)=0,pois o
terminal da carga está em aberto.
V ( x) = V (l ) cosh(γx) + ZcI (l ) senh(γx)
(2.51)
1
V (l ) senh(γx)
Zc
(2.52)
I ( x) = I (l ) cosh(γx) +
Sendo assim, temos o ganho de tensão determinado por :
V (l )
1
=
V ( x) cosh(γl )
(2.106)
Iremos no tópico seguinte de simulações, fazer as devidas correções com bancos de
reatores e capacitores, afim de buscarmos a situação desejada
V (l ) = V ( x)
(2.107)
58
3- Simulação comparativa com a linha real
Devido à necessidade de resistir a oscilação de tensão provenientes de
chaveamento, e em que estas afetam consideravelmente o custo de um sistema; é
importante uma estimativa precisa das sobretensões de chaveamento sob várias condições
de operação. Consequentemente, é necessário assegurar que, ao fazer um estudo de
sobretensões de chaveamento, se conheça quais os fatores que podem afetar o resultado e
que precisão pode ser obtida.
3.1- Análise da energização da linha em vazio
Iremos a princípio simular a linha de transmissão adotada como exemplo, fazendo a
priori as devidas simulações para energização da LT em vazio, plotando os gráficos de
corrente e tensão na entrada da linha, e no final da mesma, fazendo as devidas conclusões
acerca do trabalho envolvido. Faremos a seguir as comparações com circuito π nominal da
LT, que é o mais usual nos trabalhos, versus o circuito com parâmetros distribuídos da
linha, em que a tensão e a corrente variam em amplitude e fase ao longo da linha de
transmissão. A linha foi considerada perfeitamente simétrica e representada por duas
seções de modelo π e outro de parâmetros distribuídos.
O circuito representado para os testes de comparação está mostrado na figura 11.
Trata-se de uma linha de 345 KV com 400 km de extensão.
Figura 16- Sistema simplificado equivalente usado para os testes
A fonte foi considerada como uma indutância concentrada com impedância de
seqüência positiva e negativa iguais. O valor adotado foi de Z =180.9 Ω. Usa-se o modelo
59
π para modelagem da linha considerando o acoplamento entre as fases e o solo, como é
mostrado na figura 13.
Figura 17- Modelo π usado para simulações de chaveamento
É tomada com referência de tensão, a passagem do zero vinda do negativo para o
positivo. Aplicamos para efeito de testes comparativos com a linha real feita em EMTP.
Segundo(Hermann W. Dommel),em seus estudos de casos transientes em linhas reais como
Jaguara-Taquaril os seguintes ângulos de fase para a tensão da fonte adotados são:
FaseA = Van∠90°
(2.108)
FaseB = Vbn∠ − 30°
(2.109)
FaseC = Vcn∠210°
(2.110)
Adotamos também para abertura da chave em 1ms e fechamento da chave em
20.7ms. Os gráficos a seguir (18 à 26) , representam os valores de tensão e corrente no
período transitório, devido a energização da linha em vazio. Estes gráficos representam os
valores de tensão e corrente no momento em que é aberto e fechado a chave seccionadora.
São utilizados dois modelos simultaneamente, sendo as curvas em azul representando o
modelo de parâmetros distribuídos, e as curvas em vermelho correspondentes ao modelo
de circuitos π em cascata.
60
Figura 18- Superposição das ondas de corrente Fase_A
Figura 19- Superposição das ondas entrada Fase_A
61
Figura 20 – Superposição das ondas de saída Fase_A
Figura 21- Superposição das ondas de corrente Fase_B
62
Figura 22- Superposição das ondas entrada Fase_B
Figura 23- Superposição das ondas de saída Fase_B
63
Figura 24 – Superposição das ondas de corrente Fase_C
Figura 25 - Superposição das ondas entrada Fase_C
64
Figura 26- Superposição das ondas de saída Fase_C
Considerando a energização da linha analisada, através da obtenção das curvas de
tensão na entrada e saída da linha, podemos observar que as curvas apresentam algumas
diferenças. Isto de deve as limitações do modelo proposto, e implementado no software
utilizado em ambiente computacional. Os gráficos das figuras (20,23,26), representam as
sobretensões de manobra no período transitório no processo de chaveamento da linha em
vazio.Podemos perceber que estes picos de tensão podem chegar até 2,5 pu. As figuras
(18,21,24) mostra-se os gráficos de correntes, onde se verificam os picos no momento da
manobra no período transitório. Estes picos são responsáveis, para dimensionamento das
chaves seccionadoras de entrada de linhas de transmissão. Os demais gráficos ilustrados
acima, representam as tensões (em pu) em cada fase durante a energização.
Para situações de chaveamento ou energização da linha deve ser usado o modelo de
parâmetros dependentes da freqüência, porém o maior incoveniente da utilização deste
modelo, reside no fato de que o processo envolvendo a solução deste problema é um pouco
lento e pode demorar um pouco, visto que temos neste caso a necessidade de resolver uma
integral de convolução. Além disso, embora esse modelos sejam convenientes, os seus
resultados ainda não são confiáveis com os obtidos através do modelo de parâmetros
distribuídos com resistência concentrada, que é o modelo aqui adotado. Quando utilizado o
modelo de circuitos π em cascata e de parâmetros distribuídos para modelar a linha de
65
transmissão para estudo de caso, vimos que os resultados são satisfatórios, estando o
mesmo em consonância com os modelos apresentados por outros autores, que utilizaram o
software EMTP como ambiente computacional para obtenção de resultados de
chaveamento de linhas de transmissão em vazio.
3.2 – Análise dos vários tipos de curto circuito
As figuras (23 a 40) correspondem às tensões de entrada e saída de cada fase após a
simulação dos vários tipos de faltas existentes na linha em estudo.
Para uma situação de falta na linha C temos, os seguintes gráficos mostrados
abaixo:
Figura 27 – Curto circuito em linha não transposta(FASE C ) – Tensão na fase A , terminal inicial.
66
Figura 28 – Curto circuito em linha não transposta (FASE C ) – Tensão na fase B , terminal inicial.
Figura 29 – Curto circuito em linha não transposta (FASE C) –Tensão na fase C , terminal inicial.
67
Figura 30 – Curto circuito em linha não transposta (FASE C ) – Tensão na fase A , terminal final.
Figura 31 Curto circuito em linha não transposta (FASE C ) –Tensão na fase B , terminal final.
68
Figura 32 – Curto circuito em linha não transposta (FASE C) – Tensão na fase C,terminal final.
Podemos observar que as simulações de faltas monofásicas realizadas no ambiente
de simulação computacional, através do circuito π nominal em cascata da linha e de
parâmetros distribuídos, estão condizentes e apresentam concordância com o modelo
proposto por trabalhos apresentados em outros softwares de simulação muito utilizados
atualmente por concessionárias de energia em suas simulações. Os gráficos das figuras 30 e
31 apresentaram resultados esperados, visto que o curto monofásico ocorrido na fase C na
linha de transmissão, apresentou uma elevação de tensão nas outras fases adjacentes,
podendo chegar até o dobro da tensão de alimentação (2pu). O gráfico 32 ilustra o gráfico
de tensão do curto ocorrido na fase C, no período transitório nom terminal final da LT.
Agora com o mesmo método anteriormente descrito, foram plotados os seguintes
gráficos(33 a 38) de tensões de entrada e saída para um curto bifásico ocorrido nas Fases
AC.
69
Figura 33 – Curto circuito em linha não transposta (FASE AC) –Tensão na fase A, terminal inicial.
Figura 34 – Curto circuito em linha não transposta (FASE AC)–Tensão na fase B, terminal inicial.
70
Figura 35 – Curto circuito em linha não transposta (FASE AC) –Tensão na fase C , terminal inicial.
Figura 36–Curto circuito em linha não transposta (FASE AC)–Tensão na fase A,terminal final.
71
Figura 37–Curto circuito em linha não transposta (FASE AC)– Tensão na fase B , terminal final.
Figura 38–Curto circuito em linha não transposta (FASE AC)–Tensão na fase C , terminal final.
72
Curto circuito trifásico nas FASES A_B_C :
Figura 39 – Curto circuito Trifásico, Tensão na fase A, terminal inicial.
Figura 40 – Curto circuito Trifásico, Tensão na fase B, terminal inicial.
73
Figura 41 – Curto circuito Trifásico, Tensão na fase C, terminal inicial.
Figura 42 – Curto circuito Trifásico, Tensão na fase A, terminal final.
74
Figura 43 – Curto circuito Trifásico, Tensão na fase B, terminal final.
Figura 44 – Curto circuito Trifásico, Tensão na fase C,terminal final.
75
No caso das curvas para o terminal final da linha de transmissão analisada e considerando
o curto-circuito na fase AC desse terminal, as simulações com o modelo proposto
apresentaram resultados previsíveis e satisfatórios, como por exemplo, o gráfico da figura
37, em que a tensão na fase B do terminal final da linha, apresentava uma elevação de
tensão(Swell) de 1.8 pu. Os resultados podem ser interpretados como bons, visto pela baixa
complexidade do modelo introduzido. A representação da linha por modelos de circuitos π
e de parâmetros distribuídos, tem sido discutida atualmente, visto que ela possui algumas
limitações quanto ao seu uso.
3.3 Análise das várias situações de carga
Nessa primeira análise, estuda-se as diferentes situações que podem ocorrer no nível
de tensão nos terminais receptores da linha(Jaguara-Taquaril),sem compensação
alguma,como por exemplo, curto circuito, tensão a vazio no terminal final da linha, carga
leve, carga pesada e carregamento nominal.
Em seguida será demonstrado como podemos corrigir as tensões no final da linha,
pela compensação em paralelo com capacitores e indutores e, em seguida a compensação
em série, com capacitores.O perfil das tensões ao longo da linha de transmissão para as
diversas situações estudadas é mostrado na figura 45.
76
Figura 45 – Perfil de tensão ao longo da L.T
Para conhecer o grau de compensação adequado para reduzir o efeito ferranti,
precisaremos conhecer e calcular o ganho de tensão no final da L.T. Em primeiro lugar,
calculamos o ganho de tensão para a linha analisada sem nenhuma compensação,
seguidamente, fazemos o cálculo para sistemas com diferentes níveis de compensação.
Através de um cálculo em ambiente computacional, conseguimos encontrar esses dados
tendo como entrada de dados os parâmetros elétricos do sistema, nível de tensão e
comprimento da linha simulado. Abaixo esboçamos o diagrama de blocos referente aos
cálculos efetuados.
77
Figura 46 – D.B para obtenção do ganho de tensão sem compensação
Figura 47 – D.B para obtenção do ganho de tensão com compensação
78
Figura 48- Desenho esquemático para simulação Linha 345 KV
Na tabela 04 é mostrado os ganhos de tensão para o sistema de 345 da linha
Jaguara-Taquaril, sem compensação e com compensação reativa(40-100%) nos extremos
da linha.
Tab 4- Ganho de tensão da linha de 345 KV com compensação reativa nos extremos
Ganho para a Linha com compensação Reativa em Derivação
Sistema
Convencional
Nível de
Tensão
(KV)
345
L(Km)
150
450
900
V2
V1
1,103
1,213
2.567
Ganho de tensão com Compensação
40%
70%
80%
90%
100%
1,0115 1,0057 1,0038 1,0013 0,99925
1,1123 1,0526 1,0344 1,0163 1,00013
1,5776 1,2246 1,1387 1,0655 0,99903
Na figura 49, mostra que, para a linha(Jaguara-Taquaril), se tivéssemos 900 km de
extensão, o ganho de tensão seria de aproximadamente 2,6 ou seja, 260% da tensão da
barra emissora. Temos então o efeito ferranti bem presente, sendo então necessário a sua
compensação tanto em série através de banco de capacitores quanto em paralelo, através de
banco de indutores, para diminuir essa tensão na barra receptora e conseqüentemente
79
aumentar a potencia a ser transmitida. Na tabela 05 é mostrado os ganhos de tensão do
sistema de 345 KV, simulado com compensação capacitiva no meio da linha
(50%),compensação reativa antes e depois do capacitor série e compensação reativa nos
extremos da linha.
Figura 49- Tensão a vazio na linha p/ L até 900 Km
A figura 46 ilustra o desenho esquemático que é aplicado em nosso estudo das
situações de compensação em série e em paralelo, no meio da linha e nos seus extremos.
Figura 50 – Compensação em série e paralelo L.T
80
Tabela 5 – Ganho de tensão da linha de 345 KV, com compensação em derivação(quatro
bancos)e com capacitor no meio da linha
Ganho para a linha com Compensação Reativa em derivação
e Compensação em Série
Ganho
Sistema
Tensão
Ganho de tensão com Compensação
Convencional sem com.
Nível
deTensão L(Km)
(KV)
345
900
V2
V1
40%
70%
80%
90% 100%
2,5677 1,3112 1,1334 1,0842 1,0403 0,9997
É importante conhecer além do ganho de tensão, os dados dos reativos totais do
sistema em estudo, assim como os dados dos reativos para os diferentes níveis de
compensação em derivação analisados. Na tabela 06, são apresentados os valores dos
reativos que foram calculados através de um software apropriado para realizar tais
funções(ver diagrama de blocos figura 51), para o caso do sistema simulado com dois
bancos de compensação reativa(reatores) em derivação.
Tabela 6- Reativo total no sistema de 345 KV com compensação reativa nos
extremos
Reativo total para o caso de compensação nos extremos
Sistema
Convencional
Nível de
Tensão
em(KV)
345
L(Km)
150
450
900
V2
V1
Ganho de tensão com Compensação
Reator
40%
Reator
70%
Reator
80%
Reator
90%
Reator
100%
(MVAR)
(MVAR) (MVAR)
(MVAR)
(MVAR)
1,103 32,361 56,634 64,722 72,812 80,911
1,213 99,641 174,76 199,28 224,19 249,19
2.5677 219,29 386,82 438,42 493,23 548,03
81
Na figura 51, é representado os respectivos diagramas de blocos para determinar os
valores dos reativos para compensação em paralelo e em série da linha de transmissão.
Figura 51 - Diagrama de blocos para obtenção do Reativo
Para linhas muito longas, além de compensar a reatância transversal da linha, é
compensada também a reatância longitudinal da linha através de um capacitor série. Para
os nossos sistemas mais longos compensamos a reatância longitudinal em 50 %, que é um
nível muito utilizado nos sistemas reais. Na tabela 07 é mostrado o total da reatância
longitudinal da linha em estudo assim como o reativo série a compensar. Também mostrase o reativo compensado em 50% e o valor do capacitor série utilizado.
Tabela 07 – Reatância longitudinal e compensação em série linha 345 KV
Reatância Longitudinal e compensação série
Sistema convencional
Nível de
Tensão
(KV)
345
L(Km) X(Ω)
900
266,08
Reativo
série
(MVAR)
Comp.
Série 50%
(MVAR)
Xc(Ω)
352,45
223,71
133,015
82
4 – Resultados e discussões
Os novos sistemas de transmissão precisam de muito cuidado na abordagem dos
seus problemas, principalmente quando alguns de seus parâmetros são tomados em conta
assumindo semelhança de parâmetros com outras linhas já construídas (Linha JaguaraTaquaril). É necessário que todos os elementos relacionados à transmissão sejam
melhorados para conseguir um maior desempenho e confiabilidade do sistema.
Os estudos das simulações aqui desenvolvidos, envolvem sistemas de transmissão
reais e de grande importância para o SIN brasileiro. Cada sistema foi tratado com suas
características particulares, isto é com os dados reais das alturas dos cabos em suas torres,
distâncias entre feixes, capacitância entre os cabos e o solo, efeito dos cabos guarda, entre
outros fatores.
As simulações para linhas acima de 400 Km,no nível de tensão 345 KV(EHV)
analisados, demonstraram a necessidade da compensação reativa para reduzir o efeito
Ferranti, presente neste sistema. Podemos concluir que as simulações realizadas
considerando a linha Jaguara-Taquaril
curta de até 150 Km, não necessitam de
compensação reativa em derivação, apresentando ganho de tensão no final da linha menor
que 1,02 pu. Para linhas acima de 150 Km vimos que é necessário compensar a linha
transversalmente.
A partir dos resultados obtidos pode-se afirmar que o correto dimensionamento dos
bancos de capacitores em paralelo e em série, assim como os bancos de reatores em
paralelo, tem elevada influência, pois estes são coordenados em sintonia com relés de
subtensão e sobretensão respectivamente.
As comparações forma feitas utilizando as simulações de energização de linha e de
situações de curto-circuito. Estas simulações foram feitas utilizando um programa de
computador, onde estas são comparadas com as simulações realizadas pelo software
ATPDraw, muito utilizado pela grande maioria das concessionárias de energia em suas
simulações com transitórios. As comparações foram realizadas no domínio do tempo,
sendo a tensão o seu principal foco de interesse. Nesta etapa, foi utilizada uma linha do
sistema Furnas, localizada no estado de Minas Gerais, entre as subestações de Jaguara e
Taquaril. Tal linha é uma linha trifásica simples e é reportada como o único caso de
simulação em linha real e que serviu de base para os nossos estudos e simulações
realizadas. Os resultados obtidos tiveram boas aproximações em relação aos resultados
correspondentes obtidos por ferramentas computacionais de simulação já consagradas
nessa área de sistemas elétricos de potência. Finalmente conclui-se que, com a escassez das
83
fontes primárias de energia próximas dos grandes centros consumidores e grandes
distâncias das fontes ainda não explorados destes centros é de suma importância um
planejamento e manutenção adequados nas linhas de transmissão já existentes, evitando a
interrupção e, com isso, um maior aproveitamento.
Para possíveis trabalhos futuros podem ser destacados alguns itens, tais como:
-Analisar a influência do nível de tensão de energização na abertura dos disjuntores
e chaves seccionadoras.
-Através dos valores obtidos de tensão de energização, sabermos o correto
dimensionamento das chaves seccionadoras de entrada da linha.
-Analisar o comportamento do arco elétrico existente nas chaves e nos disjuntores,
mediante os vários tipos de curtos aplicados.
84
5 – Referências Bibliográficas
[1]Willian D. Stevenson Jr. 1974, McGRAW-HILL
[2]Case Studies for Eletromagnetic Transients, 2nd edition – Herman W. Dommel
[3]Operador Nacional do sistema elétrico (ONS), Sistema interligado nacional operação interligada Sudeste
[4]A.Greenwood, Eletrical Transients in Power Systems, Wiley-interscience, 2nd
edition, New York, 1991.
[5]Matrizes de Transformação Reais Aplicadas as Linhas de Circuito Duplo, José
C. C. Campos, Ds –Unicamp,2009.
[6] Análise de Sensibilidade da Corrente de Arco Secundário para diferentes linhas
de Transmissão, Milton Elvis Zevallos Alcahuaman, Ds – Unicamp,2007.
[7] A. D'AJUZ, C. S. FONSECA, F. M. S. CARVALHO, J. AMON
FILHO, L. E. N. DIAS, M. P. PEREIRA, P. C. V. ESMERALDO, R. VAISMAN,
S. O. FRONTIN, Transitórios Elétricos e Coordenação de Isolamento - Aplicação em
Sistemas de Potência de Alta Tensão, Editora da Universidade Fluminense (EDUFF) e
FURNAS Centrais Elétricas, Niterói, Rio de Janeiro, 1987.
[8] “Transmissão de Energia Elétrica: Linhas Aéreas; teoria das Linhas em Regime
Permanente”, R.D. Fuchs, Livros Técnicos e Científicos Editora S.A, Rio de Janeiro,
R.J.,1977.
[9] Antonio C. C. de Carvalho, Carlos M. Portela, Marta Lacorte, e Roberto
Colombo “Disjuntores e Chaves – Aplicação em Sistemas de Potência”, Capítulo 11: A
Teoria do Arco Elétrico nos Disjuntores e Chaves de Alta-tensão, CE 13 do CIGRÉ –
Brasil, FURNAS / UFF, 1996.
85