ExerciciosRefração luminosaXX

Refração luminosa
Parte I
1. (Enem 2010) Um grupo de cientistas liderado por
pesquisadores do Instituto de Tecnologia da Califórnia
(Caltech), nos Estados Unidos, construiu o primeiro
metamaterial que apresenta valor negativo do índice de
refração relativo para a luz visível. Denomina-se
metamaterial um material óptico artificial, tridimensional,
formado por pequenas estruturas menores do que o
comprimento de onda da luz, o que lhe dá propriedades e
comportamentos que não são encontrados em materiais
naturais. Esse material tem sido chamado de “canhoto”.
a) o comprimento de onda diminui e a velocidade aumenta.
b) o comprimento de onda e a frequência da luz diminuem.
c) a frequência aumenta, mas o comprimento de onda
diminui.
d) a frequência não se altera e o comprimento de onda
diminui.
e) a frequência não se altera e o comprimento de onda
aumenta.
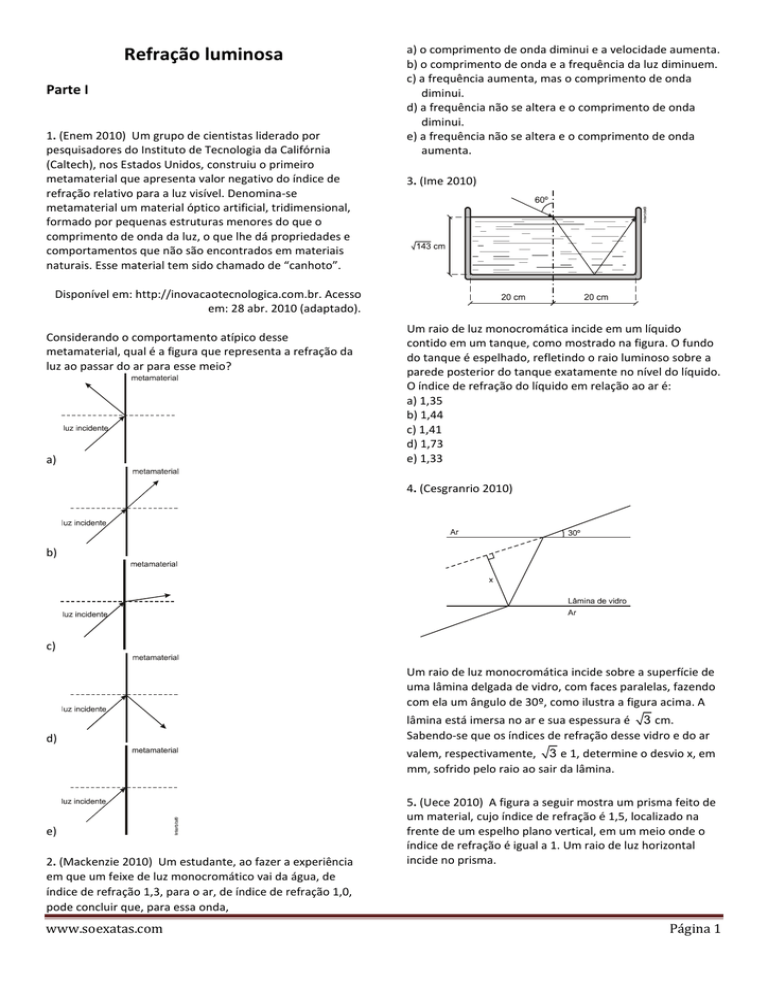
3. (Ime 2010)
Disponível em: http://inovacaotecnologica.com.br. Acesso
em: 28 abr. 2010 (adaptado).
Considerando o comportamento atípico desse
metamaterial, qual é a figura que representa a refração da
luz ao passar do ar para esse meio?
a)
Um raio de luz monocromática incide em um líquido
contido em um tanque, como mostrado na figura. O fundo
do tanque é espelhado, refletindo o raio luminoso sobre a
parede posterior do tanque exatamente no nível do líquido.
O índice de refração do líquido em relação ao ar é:
a) 1,35
b) 1,44
c) 1,41
d) 1,73
e) 1,33
4. (Cesgranrio 2010)
b)
c)
Um raio de luz monocromática incide sobre a superfície de
uma lâmina delgada de vidro, com faces paralelas, fazendo
com ela um ângulo de 30º, como ilustra a figura acima. A
d)
lâmina está imersa no ar e sua espessura é 3 cm.
Sabendo-se que os índices de refração desse vidro e do ar
valem, respectivamente, 3 e 1, determine o desvio x, em
mm, sofrido pelo raio ao sair da lâmina.
e)
2. (Mackenzie 2010) Um estudante, ao fazer a experiência
em que um feixe de luz monocromático vai da água, de
índice de refração 1,3, para o ar, de índice de refração 1,0,
pode concluir que, para essa onda,
www.soexatas.com
5. (Uece 2010) A figura a seguir mostra um prisma feito de
um material, cujo índice de refração é 1,5, localizado na
frente de um espelho plano vertical, em um meio onde o
índice de refração é igual a 1. Um raio de luz horizontal
incide no prisma.
Página 1
c)
d)
o
o
Sabendo que sen(6 ) ≈ 0,104 e sen(9 ) = 0,157, o ângulo de
reflexão no espelho é de
o
a) 2 .
o
b) 3 .
o
c) 4 .
o
d) 6 .
6. (Pucrj 2010) Uma onda eletromagnética se propaga no
vácuo e incide sobre uma superfície de um cristal fazendo
o
um ângulo de θ1 = 60 com a direção normal a superfície.
Considerando a velocidade de propagação da onda no
8
vácuo como c = 3 x 10 m/s e sabendo que a onda refratada
o
faz um ângulo de θ2 = 30 com a direção normal, podemos
dizer que a velocidade de propagação da onda no cristal em
m/s é
8
a) 1 × 10
8
b) 2 × 10
8
c) 3 × 10
8
d) 4 × 10
8
e) 5 × 10
7. (Ufmg 2010) Um arco-íris forma-se devido à dispersão
da luz do Sol em gotas de água na atmosfera.
Após incidir sobre gotas de água na atmosfera, raios de luz
são refratados; em seguida, eles são totalmente refletidos e
novamente refratados.
Sabe-se que o índice de refração da água para a luz azul é
maior que para a luz vermelha.
Considerando essas informações, assinale a alternativa em
que estão mais bem representados os fenômenos que
ocorrem em uma gota de água e dão origem a um arco-íris.
8. (Udesc 2010) Um bastão é colocado sequencialmente
em três recipientes com líquidos diferentes. Olhando-se o
bastão através de cada recipiente, observam-se as imagens
I, II e III, conforme ilustração a seguir, pois os líquidos são
transparentes. Sendo nAr, nI, nII e nIII os índices de refração
do ar, do líquido em I, do líquido em II e do líquido em III,
respectivamente, a relação que está correta é:
a) nAr < nI < nII
b) nII < nAr < nIII
c) nI > nII > nIII
d) nIII > nII > nI
e) nIII < nI < nII
9. (Ufg 2010) Um raio de luz monocromático incide
perpendicularmente na face A de um prisma e sofre
reflexões internas totais com toda luz emergindo pela face
C, como ilustra a figura a seguir. Considerando o exposto e
sabendo que o meio externo é o ar ( n a r = 1 ) , calcule o
índice de refração mínimo do prisma.
10. (Ufpr 2010) Descartes desenvolveu uma teoria
para explicar a formação do arco-íris com base nos
conceitos da óptica geométrica.
Ele supôs uma gota de água com forma esférica e a
incidência de luz branca conforme mostrado de modo
simplificado na figura.
a)
b)
www.soexatas.com
Página 2
O raio incidente sofre refração ao entrar na gota
(ponto A) e apresenta uma decomposição de cores. Em
seguida, esses raios sofrem reflexão interna dentro da gota
(região B) e saem para o ar após passar por uma segunda
refração (região C).
Posteriormente, com a experiência de Newton
com prismas, foi possível explicar corretamente a
decomposição das cores da luz branca. A figura não está
desenhada em escala e, por simplicidade, estão
representados apenas os raios violeta e vermelho, mas
deve-se considerar que entre eles estão os raios das outras
cores do espectro visível.
Sobre esse assunto, avalie as seguintes afirmativas:
1. O fenômeno da separação de cores quando a luz sofre
refração ao passar de um meio para outro é chamado de
dispersão.
2. Ao sofrer reflexão interna, cada raio apresenta ângulo de
reflexão igual ao seu ângulo de incidência, ambos
medidos em relação à reta normal no ponto de
incidência.
3. Ao refratar na entrada da gota (ponto A na figura), o
violeta apresenta menor desvio, significando que o
índice de refração da água para o violeta é menor que
para o vermelho.
córnea e das demais estruturas do olho são muito próximos
do índice de refração da água (n água=
4
). Por isso usamos
3
máscaras de mergulho, o que interpõe uma pequena
camada de ar (n ar=1) entre a água e o olho. Um peixe está
a uma distância de 2,0m de um mergulhador. Suponha o
vidro da máscara plano e de espessura desprezível.
Calcule a que distância o mergulhador vê a imagem do
peixe. Lembre-se que para ângulos pequenos sen(a)>tan(a).
13. (Ufpe 2001) Qual das figuras a seguir melhor
representa a trajetória de um raio de luz monocromática,
ao atravessar uma janela de vidro (imersa no ar) de
espessura d?
Assinale a alternativa correta.
a) Somente a afirmativa 1 é verdadeira.
b) Somente a afirmativa 2 é verdadeira.
c) Somente as afirmativas 1 e 2 são verdadeiras.
d) Somente as afirmativas 1 e 3 são verdadeiras.
e) Somente as afirmativas 2 e 3 são verdadeiras.
11. (Ufrn 2001) Uma fibra ótica, mesmo encurvada,
permite a propagação de um feixe luminoso em seu
interior, de uma extremidade à outra, praticamente sem
sofrer perdas (veja a figura a seguir).
14. (Unesp 1996) Na figura, estão representados um
°
prisma retangular, cujos ângulos da base são iguais a 45 ,
um objeto AB e o olho de um observador.
Devido ao fenômeno da reflexão total, os raios de luz
provenientes do objeto são refletidos na base do prisma,
que funciona como um espelho plano.
Assinale a alternativa que melhor representa a imagem
A'B', vista pelo observador.
A explicação física para o fato acima descrito é a seguinte:
Como o índice de refração da fibra ótica, em relação ao
índice de refração do ar, é
a) baixo, ocorre a reflexão interna total.
b) alto, ocorre a reflexão interna total.
c) alto, a refração é favorecida, dificultando a saída do feixe
pelas laterais.
d) baixo, a refração é favorecida, dificultando a saída do
feixe pelas laterais.
12. (Ufrj 2001) Temos dificuldade em enxergar com
nitidez debaixo da água porque os índices de refração da
www.soexatas.com
Página 3
TEXTO PARA A PRÓXIMA QUESTÃO:
Na(s) questão(ões) a seguir escreva nos parênteses a soma
dos itens corretos.
15. (Ufba 1996) A figura a seguir representa um raio de luz
monocromática R, que incide na base de um recipiente de
vidro que contém uma camada de água. Considerem-se:
°
°
°
sen19 = 0,33; sen 30 = 0,50; sen 60 = 0,86; e os índices de
refração do vidro, da água e do ar respectivamente iguais a
1,5, 1,3 e 1,0.
Dados: sendo os ângulos α e β pequenos, considere
tgα ≅ senα e tgβ ≅ senβ.
índice de refração da água: nágua=1,33
índice de refração do ar: nar=1
a) 0,80 m
b) 1,00 m
c) 1,10 m
d) 1,20 m
e) 1,33 m
2. (Fuvest 2014) Um prisma triangular desvia um feixe de
luz verde de um ângulo θA , em relação à direção de
incidência, como ilustra a figura A, abaixo.
Nessas condições, é correto afirmar:
01) Quando a luz passa do ar para o vidro, a sua velocidade
de propagação é alterada.
02) Uma parcela da luz incidente será refletida sob um
°
ângulo de 30 em relação ao plano da lâmina de vidro.
04) Uma parcela da luz incidente será absorvida pelo vidro.
08) O raio de luz sofrerá reflexão total, ao passar do vidro
para a água.
16) Haverá um raio de luz refratado da água para o ar.
Parte II
1. (Espcex (Aman) 2014) Uma fonte luminosa está fixada
no fundo de uma piscina de profundidade igual a 1,33 m.
Uma pessoa na borda da piscina observa um feixe luminoso
monocromático, emitido pela fonte, que forma um
pequeno ângulo α com a normal da superfície da água, e
que, depois de refratado, forma um pequeno ângulo β
com a normal da superfície da água, conforme o desenho.
A profundidade aparente “h” da fonte luminosa vista pela
pessoa é de:
www.soexatas.com
Se uma placa plana, do mesmo material do prisma, for
colocada entre a fonte de luz e o prisma, nas posições
mostradas nas figuras B e C, a luz, ao sair do prisma, será
desviada, respectivamente, de ângulos θB e θC , em
relação à direção de incidência indicada pela seta. Os
desvios angulares serão tais que
a) θA = θB = θC
b) θ A > θB > θC
c) θA < θB < θC
d) θA = θB > θC
e) θA = θB < θC
3. (Ufpr 2013) Ao ser emitida por uma fonte, uma luz
monocromática, cujo comprimento de onda no ar é λ 0 ,
incide no olho de uma pessoa. A luz faz o seguinte percurso
até atingir a retina: ar – córnea – humor aquoso – cristalino
– humor vítreo. Considerando que o índice de refração do
ar é n0 = 1,00, da córnea é n1 = 1,38, do humor aquoso é
n2 = 1,33, do cristalino é n3 = 1,40 e do humor vítreo é
n4 = 1,34 e que λ1, λ 2 , λ 3 e λ 4 são os comprimentos
de onda da luz na córnea, no humor aquoso, no cristalino e
no humor vítreo, respectivamente, assinale a alternativa
correta.
a) λ1 < λ 0 .
b) λ 2 < λ1.
c) λ 3 > λ 2 .
d) λ 4 < λ 3 .
Página 4
e) λ 4 > λ 0 .
4. (Ufg 2013) Refratômetro é um instrumento ótico
utilizado para medir o índice de refração de uma substância
e também para determinar a concentração de certas
substâncias, como, por exemplo, o açúcar em um fluido
qualquer. A figura ilustra o protótipo de um refratômetro
constituído por um prisma de índice de refração 1,6, um
orifício no qual entra a luz de análise e uma cavidade para
colocar o material líquido a ser analisado. Nessas
condições, um feixe de luz monocromático, ao entrar pelo
orifício, refrata na interface prisma-líquido e atinge a escala
graduada em um ponto a 4 cm da origem.
Uma esfera de gelo de raio R flutua parcialmente imersa
em um copo com água, como mostra a figura acima. Com a
finalidade de iluminar uma bolha de ar, também esférica,
localizada no centro da esfera de gelo, utilizou-se um feixe
πR2 2
m que
100
incide verticalmente na esfera. Considerando que os raios
mais externos do feixe refratado tangenciam a bolha
conforme a figura, determine a massa específica do gelo.
Dados: Índice de refração do ar: 1,0; Índice de refração do
3
gelo: 1,3; Massa específica do ar: 1,0 kg/m ; Massa
3
3
específica da água: 10 kg/m ; Volume da calota esférica:
luminoso de seção reta circular de área
v = 2 ⋅ 10−2 πR3 .
7. (Ufpa 2013) O arco-íris é um fenômeno óptico que
acontece quando a luz branca do Sol incide sobre gotas
esféricas de água presentes na atmosfera. A figura abaixo
mostra as trajetórias de três raios de luz, um vermelho
(com comprimento de onda λ = 700 nm), um verde
( λ = 546 nm )
e um violeta ( λ = 436 nm ) , que estão num
plano que passa pelo centro de uma esfera (também
mostrada na figura). Antes de passar pela esfera, estes raios
fazem parte de um raio de luz branca incidente.
Considerando-se que L = 12 cm e h = 2 cm, calcule:
a) O índice de refração do líquido sob análise.
b) O menor índice de refração que esse instrumento
permite medir.
5. (Uerj 2013) Um raio luminoso monocromático,
inicialmente deslocando-se no vácuo, incide de modo
perpendicular à superfície de um meio transparente, ou
seja, com ângulo de incidência igual a 0°. Após incidir sobre
5
essa superfície, sua velocidade é reduzida a
do valor no
6
vácuo.
sen θ1 θ1
Utilizando a relação
=
para ângulos menores
sen θ2 θ2
que 10°, estime o ângulo de refringência quando o raio
atinge o meio transparente com um ângulo de incidência
igual a 3°.
6. (Ime 2013)
Analisando as trajetórias destes raios quando passam do
meio para a esfera e da esfera, de volta para o meio, é
correto afirmar que
a) o índice de refração da esfera é igual ao índice de
refração do meio.
b) o índice de refração da esfera é maior do que o do meio
e é diretamente proporcional ao comprimento de onda
( λ ) da luz.
c) o índice de refração da esfera é maior do que o do meio
e é inversamente proporcional ao comprimento de onda
( λ ) da luz.
d) o índice de refração da esfera é menor do que o do meio
e é diretamente proporcional ao comprimento de onda
( λ ) da luz.
e) o índice de refração da esfera é menor do que o do meio
e é inversamente proporcional ao comprimento de onda
( λ ) da luz.
8. (Ufg 2013) Um feixe de luz branca é empregado para
transmitir sinais de telecomunicação. Para isso, é instalada
www.soexatas.com
Página 5
uma fibra óptica que possui índice de refração para o azul
de 1,528 e para o vermelho de 1,513. Considerando-se os
raios de luz azul e vermelho e que a distância entre duas
cidades quaisquer é de 300 km, determine:
a) o raio de luz que chega primeiro. Justifique;
b) o atraso entre os raios ao percorrerem essa distância.
Dado:
c = 3 ⋅ 108 m / s
9. (Ibmecrj 2013) Um raio de luz monocromática se
propaga do meio A para o meio B, de tal forma que o
ângulo de refração β vale a metade do ângulo de
incidência α . Se o índice de refração do meio A vale 1 e o
sen β = 0,5 , o índice de refração do meio B vale:
a)
b)
c)
d)
e)
2
3
3
0,75
0,5
10. (Epcar (Afa) 2013) A figura abaixo mostra uma face de
um arranjo cúbico, montado com duas partes
geometricamente iguais. A parte 1 é totalmente preenchida
com um líquido de índice de refração n1 e a parte 2 é um
bloco maciço de um material transparente com índice de
refração n2 .
Considere que todos os meios sejam homogêneos,
transparentes e isotrópicos, e que a interface entre eles
forme um dióptro perfeitamente plano.
Nessas condições, é correto afirmar que o índice de
refração n3 pode ser igual a
a) 1,5 n1
b) 1,3 n1
c) 1,2 n1
d) 1,1n1
11. (Ufg 2013) Leia o texto a seguir.
O processo de unificação se faz por intermédio do que se
chama de redes. Seria, portanto, pela unificação que adviria
o fracionamento. As redes são vetores de modernidade e
também de entropia. Mundiais, veiculam um princípio de
ordem, uma regulação a serviço de atores hegemônicos na
escala planetária.
SANTOS, M. Técnica, espaço e tempo: Meio técnicocientífico-informacional. São Paulo: Hucitec, 1994. p. 28.
O texto indica as transformações que passaram a
caracterizar o mundo globalizado. Para que essa mudança
se concretizasse era preciso consolidar um sistema
mundial, conectado em redes, e capaz de transmitir dados
e vozes em velocidades cada vez maiores e com melhores
qualidades. Uma nova tecnologia passou a converter os
dados digitalizados com a maior velocidade possível, por
meio de um sistema no qual a informação é basicamente
canalizada. Isso tornou as conexões na internet mais
rápidas, diminuindo o tempo para transferências e cópias
de arquivos.
As vias utilizadas nesse tipo de transmissão de informação e
o fenômeno físico fundamental para seu funcionamento
são, respectivamente,
a) os sinais de satélite e a reflexão interna total.
b) as fibras ópticas e a difração.
c) os sinais de rádio e a reflexão de ondas.
d) as fibras ópticas e a reflexão interna total.
e) os sinais de satélite e a difração.
12. (Unesp 2013) Uma haste luminosa de 2,5 m de
comprimento está presa verticalmente a uma boia opaca
circular de 2,26 m de raio, que flutua nas águas paradas e
transparentes de uma piscina, como mostra a figura.
Devido à presença da boia e ao fenômeno da reflexão total
da luz, apenas uma parte da haste pode ser vista por
observadores que estejam fora da água.
Neste arranjo, um raio de luz monocromático, saindo do
ponto P, chega ao ponto C sem sofrer desvio de sua direção
inicial.
Retirando-se o líquido n1 e preenchendo-se
completamente a parte 1 com um outro líquido de índice
de refração n3 , tem-se que o mesmo raio, saindo do ponto
P, chega integralmente ao ponto D.
www.soexatas.com
Página 6
Considere que o índice de refração do ar seja 1,0, o da água
4
da piscina , sen 48,6° = 0,75 e tg 48,6° = 1,13. Um
3
observador que esteja fora da água poderá ver, no máximo,
uma porcentagem do comprimento da haste igual a
a) 70%.
b) 60%.
c) 50%.
d) 20%.
e) 40%.
13. (Ita 2013) Um raio horizontal de luz monocromática
atinge um espelho plano vertical após incidir num prisma
com abertura de 4º e índice de refração n = 1,5. Considere
o sistema imerso no ar e que tanto o raio emergente do
prisma como o refletido pelo espelho estejam no plano do
papel, perpendicular ao plano do espelho, como mostrado
na figura. Assinale a alternativa que indica respectivamente
o ângulo e o sentido em que deve ser girado o espelho em
torno do eixo perpendicular ao plano do papel que passa
pelo ponto O, de modo que o raio refletido retorne
paralelamente ao raio incidente no prisma.
a) COMPLETE, na figura, a trajetória do feixe até sair do
prisma.
b) EXPLIQUE, detalhando seu raciocínio, o que acontece
com esse feixe na superfície oposta ao ângulo reto.
c) Ariete observa a dispersão da luz branca nesse
experimento? JUSTIFIQUE sua resposta.
15. (Ufg 2013) Uma lente convergente de vidro possui
distância focal f quando imersa no ar. Essa lente é
mergulhada em glicerina, um tipo de álcool com índice de
refração maior que o do ar. Considerando-se que o índice
de refração do vidro é o mesmo da glicerina (iguais a 1,5),
conclui-se que o diagrama que representa o
comportamento de um feixe de luz incidindo sobre a lente
imersa na glicerina é o seguinte:
a)
b)
a) 4º, sentido horário.
b) 2º, sentido horário.
c) 2º, sentido anti-horário.
d) 1º, sentido horário.
e) 1º, sentido anti-horário.
c)
d)
14. (Ufmg 2013) Ariete deseja estudar o fenômeno da
dispersão da luz branca, ou seja, a sua decomposição em
várias cores devido à dependência do índice de refração do
material com a frequência. Para isso, ela utiliza um prisma
de vidro cuja seção reta tem a forma de um triângulo
retângulo isósceles.
O índice de refração desse vidro é n = 1,50 para a luz
branca e varia em torno desse valor para as várias cores do
espectro visível.
Ela envia um feixe de luz branca em uma direção
perpendicular a uma das superfícies do prisma que formam
o ângulo reto, como mostrado na figura.
e)
TEXTO PARA A PRÓXIMA QUESTÃO:
DADOS:
sen 45° = 0,71; sen 60° = 0,87; cos 60° = 0,50
sen 36,9° = 0,60; cos 36,9° = 0,80
aceleração da gravidade = 10 m / s2
c = velocidade da luz = 3 × 108 m / s
16. (Cefet MG 2013) A figura a seguir representa uma onda
plana cuja velocidade de propagação e frequência no meio
1 são 14,2 m/s e 20,0 Hz, respectivamente.
(Dados: sen 45° = cos 45° = 0,707.)
www.soexatas.com
Página 7
Num determinado momento, o vagão é acelerado
horizontalmente para a esquerda com aceleração
3
g e, nessa nova situação, o
3
ângulo de incidência do raio, neste dióptro plano, passa a
ser θ2 . Considerando que a aceleração gravitacional no
local é constante e possui módulo igual a g, a razão entre os
senos dos ângulos de refração dos raios refratados na
primeira e na segunda situações, respectivamente, é
1
a)
2
b) 1
c) 2
d) 3
constante de módulo a =
Após refratar-se, o valor do comprimento de onda, em
metros, é
a) 0,500.
b) 0,750.
c) 2,00.
d) 11,6.
e) 17,4.
17. (Ufrgs 2012) Um estudante, para determinar a
velocidade da luz num bloco de acrílico, fez incidir um feixe
de luz sobre o bloco. Os ângulos de incidência e refração
medidos foram, respectivamente, 45° e 30º.

1
2
 Dado : sen 30° = ; sen 45° =

2
2 

Sendo c a velocidade de propagação da luz no ar, o valor
obtido para a velocidade de propagação da luz no bloco é
c
a) .
2
c
.
b)
2
c) c.
d) 2 c.
e) 2c.
18. (Epcar (Afa) 2012) Considere um recipiente fixo
contendo um líquido em repouso no interior de um vagão
em movimento retilíneo e uniforme que se desloca para a
direita. A superfície de separação entre o líquido e o ar
contido no vagão forma um dióptro perfeitamente plano
que é atravessado por um raio luminoso monocromático
emitido por uma fonte F fixa no teto do vagão, como
mostra a figura abaixo. Nessa condição, o ângulo de
incidência do raio luminoso é θ1 = 60°.
19. (Pucrj 2012) Um feixe luminoso se propagando no ar
incide em uma superfície de vidro. Calcule o ângulo que o
feixe refratado faz com a normal à superfície sabendo que o
ângulo de incidência θ i é de 60° e que os índices de
refração do ar e do vidro, ηar e ηvidro , são
respectivamente 1,0 e
a) 30°
b) 45°
c) 60°
d) 73°
e) 90°
3.
20. (Uem 2012) Um prisma, com ângulo de refringência 60°
e índice de refração 1,6 para luz vermelha, e 1,5 para luz
violeta, está imerso no ar, cujo índice de refração absoluto
é 1,0. Com base nessas informações, assinale o que for
correto.
01) Quando a luz violeta incide em uma das faces do
prisma, fazendo um ângulo de 49º com a linha normal a
essa superfície, ela emerge do prisma, na outra
superfície, fazendo um ângulo de 49º com sua normal.
(Dados: sen 49º ~0,75)
02) Quando a luz vermelha incide em uma das faces do
prisma, fazendo um ângulo de 53º com a linha normal a
essa superfície, ela emerge do prisma, na outra
superfície, fazendo um desvio de ~46º. (Dados: sen 53º
~0,80)
04) Esse prisma não pode ser usado como prisma de
reflexão para as radiações visíveis, pois seus índices de
refração para essas radiações são maiores que os
índices do ar.
08) Quando a luz violeta incide em uma das faces do
prisma, fazendo um ângulo de 49º com a linha normal a
essa superfície, ela sofre desvio mínimo. (Dados: sen
49º ~0,75)
16) Esse prisma é um prisma de dispersão, pois tem a
capacidade de separar a luz branca em seus
componentes do espectro eletromagnético.
TEXTO PARA A PRÓXIMA QUESTÃO:
Dados:
www.soexatas.com
Página 8
Aceleração da gravidade: 10 m/s2 .
Densidade do mercúrio: 13,6 g/cm3 .
Pressão atmosférica: 1,0 ⋅ 105 N/m2 .
Constante eletrostática:
k 0 = 1 4 πε0 = 9,0 ⋅ 109 N ⋅ m2 /C2 .
21. (Ufpe 2012) Um raio de luz incide na parte curva de um
cilindro de plástico de seção semicircular formando um
ângulo θi com o eixo de simetria. O raio emerge na face
plana formando um ângulo θr com o mesmo eixo. Um
estudante fez medidas do ângulo θr em função do ângulo
θi e o resultado está mostrado no gráfico θr versus θi .
Determine o índice de refração deste plástico.
Nessas condições, quando a luz visível incide
perpendicularmente em uma das faces do bloco e atravessa
a bolha, o objeto se comporta, aproximadamente, como
a) uma lente divergente, somente se n > 1,4.
b) uma lente convergente, somente se n > 1,4.
c) uma lente convergente, para qualquer valor de n.
d) uma lente divergente, para qualquer valor de n.
e) se a bolha não existisse, para qualquer valor de n.
23. (Uerj 2011) Um raio de luz vindo do ar, denominado
meio A, incide no ponto O da superfície de separação entre
esse meio e o meio B, com um ângulo de incidência igual a
7º.
No interior do meio B, o raio incide em um espelho côncavo
E, passando pelo foco principal F.
O centro de curvatura C do espelho, cuja distância focal é
igual a 1,0 m, encontra-se a 1,0 m da superfície de
separação dos meios A e B.
Observe o esquema:
Considere os seguintes índices de refração:
- nA = 1,0 (meio A)
- nB = 1,2 (meio B)
Determine a que distância do ponto O o raio emerge, após
a reflexão no espelho.
22. (Fuvest 2011) Um objeto decorativo consiste de um
bloco de vidro transparente, de índice de refração igual a
1,4, com a forma de um paralelepípedo, que tem, em seu
interior, uma bolha, aproximadamente esférica, preenchida
com um líquido, também transparente, de índice de
refração n. A figura a seguir mostra um perfil do objeto.
24. (Ita 2011) Um hemisfério de vidro maciço de raio de 10
cm e índice de refração n = 3/2 tem sua face plana apoiada
sobre uma parede, como ilustra a figura.
Um feixe colimado de luz de 1 cm de diâmetro incide sobre
a face esférica, centrado na direção do eixo de simetria do
hemisfério. Valendo-se das aproximações de ângulos
www.soexatas.com
Página 9
pequenos, sen θ ≈ θ e tg θ ≈ θ , o diâmetro do círculo de
luz que se forma sobre a superfície da parede é de
a) 1 cm.
2
b) cm.
3
1
c) cm.
2
1
d) cm.
3
1
e)
cm.
10
25. (Epcar (Afa) 2011) Três raios de luz monocromáticos
correspondendo às cores vermelho (Vm), amarelo (Am) e
violeta (Vi) do espectro eletromagnético visível incidem na
superfície de separação, perfeitamente plana, entre o ar e a
água, fazendo o mesmo ângulo θ com essa superfície,
como mostra a figura abaixo.
Sabe-se que α , β , e γ são, respectivamente, os ângulos
de refração, dos raios vermelho, amarelo e violeta, em
relação à normal no ponto de incidência. A opção que
melhor representa a relação entre esses ângulos é
a) α > β > γ
b) α > γ > β
c) γ > β > α
d) β > α > γ
diferentes ângulos de incidência θ e obtém o gráfico
mostrado na figura (b).
a) Qual é a razão entre n1 e n2 ?
b) À medida que o ângulo θ é aumentado, o raio refratado
deve se afastar ou se aproximar da normal? Justifique
sua resposta.
c) Qual é a razão entre as intensidades da luz refletida I1 e
refratada I2 quando θ = 35° ?
2. (Ufjf 2007) A "miragem" ocorre devido ao fato de que o
ar quente acima da superfície terrestre, como a areia do
deserto ou o asfalto num dia ensolarado, reflete o "céu",
fazendo com que tenhamos a impressão da existência de
água. Admita que o ar na região logo acima da superfície
(figura adiante) possa ser considerado como a sobreposição
de camadas muito finas de ar. Se o ar da camada superior
tem um índice de refração n0 e cada camada subsequente
tem um índice de refração 0,99 vezes o índice de refração
da camada de ar logo acima, como mostra a figura a seguir,
calcule:
Parte III
TEXTO PARA A PRÓXIMA QUESTÃO:
Use quando necessário:
- Aceleração da gravidade g = 10m / s2 ; Densidade da
água ρ = 1,0g / cm3 = 1000kg / m3
- Velocidade da luz no vácuo c = 3,0 × 108 m / s
- Constante de Planck
h = 6,63 × 10 −34 J × s = 4,14 × 10−15 eV × s;
- Constante π = 3,14
1. (Ufjf 2012) A figura (a) mostra uma interface de
separação entre dois meios ópticos de índices de refração
n1 e n2 . Quando um raio de luz de intensidade I0 incide
sobre a interface com um ângulo θ em relação à normal,
observa-se a presença de um raio de luz refletido de
intensidade I1 e um raio de luz refratado de intensidade
I2 . Um estudante de Física mede a razão R = I1 I0 para
www.soexatas.com
a) o seno do ângulo de refração sofrido por um raio de luz
°
que incida com um ângulo θ0 = 60 da camada superior para
a camada subsequentemente abaixo.
b) o seno do ângulo de refração na i-ésima camada do
mesmo raio incidente do item a).
c) o número de camadas de ar necessárias para que ocorra
a reflexão total do raio do item a), supondo que a reflexão
total ocorra na última camada.
3. (Ufjf 2006) O arco-íris é causado pela dispersão da luz do
Sol que sofre refração e reflexão pelas gotas de chuva
(aproximadamente esféricas). Quando você vê um arco-íris,
o Sol está:
a) na sua frente.
b) entre você e o arco-íris.
Página 10
c) em algum lugar atrás do arco-íris.
d) atrás de você.
e) em qualquer lugar, pois não importa a posição do Sol.
4. (Ufjf 2002) Na figura a seguir, está esquematizado um
aparato experimental que é utilizado para estudar o
aumento do número de bactérias numa solução líquida
(meio de cultura), através de medidas de ângulos de
refração. Um feixe de luz monocromático I, produzido por
um laser, incide do ar para a solução, fazendo um ângulo θi
com a normal à superfície líquida. A densidade absoluta
inicial da solução, quando as bactérias são colocadas nela, é
3
1,05g/cm . Para esse valor da densidade absoluta, o ângulo
°
de refração medido é θr = 45 . O índice de refração da
solução, ns, varia em função da densidade absoluta ρ de
é dada por I0 =
P0
, em que P0 é a potência da
4πd 2
fonte. Sendo P0 = 24 W, calcule a intensidade luminosa
que atravessa um polarizador que se encontra a d = 2 m
da fonte e para o qual θ = 60°.
b) Uma maneira de polarizar a luz é por reflexão. Quando
uma luz não polarizada incide na interface entre dois
meios de índices de refração diferentes com o ângulo de
incidência θB , conhecido como ângulo de Brewster, a
luz refletida é polarizada, como mostra a figura abaixo.
Nessas condições, θB + θr = 90°, em que θr é o ângulo
do raio refratado. Sendo n1 = 1,0 o índice de refração do
meio 1 e θB = 60°, calcule o índice de refração do meio
2.
acordo com a expressão ns=C ρ .
a) Com base na expressão para ns acima, encontre uma
unidade para a constante C.
b) À medida em que o tempo passa, o número de bactérias
aumenta, assim como a densidade da solução. Num certo
instante, mede-se o ângulo de refração em relação à
°
normal e encontra-se o valor 30 , para o mesmo ângulo de
incidência do feixe. Calcule a densidade absoluta da solução
neste instante.
2. (Fuvest 2011) Um jovem pesca em uma lagoa de água
transparente, utilizando, para isto, uma lança. Ao enxergar
um peixe, ele atira sua lança na direção em que o observa.
O jovem está fora da água e o peixe está 1 m abaixo da
superfície. A lança atinge a água a uma distância x = 90 cm
da direção vertical em que o peixe se encontra, como
ilustra a figura abaixo. Para essas condições, determine:
a) O ângulo α , de incidência na superfície da água, da luz
refletida pelo peixe.
b) O ângulo β que a lança faz com a superfície da água.
c) A distância y, da superfície da água, em que o jovem
enxerga o peixe.
Parte IV
1. (Unicamp 2013) O efeito de imagem tridimensional no
cinema e nos televisores 3D é obtido quando se expõe cada
olho a uma mesma imagem em duas posições ligeiramente
diferentes. Um modo de se conseguir imagens distintas em
cada olho é através do uso de óculos com filtros
polarizadores.
a) Quando a luz é polarizada, as direções dos campos
elétricos e magnéticos são bem definidas. A intensidade
da luz polarizada que atravessa um filtro polarizador é
2
dada por I = I0 cos θ, onde I0 é a intensidade da luz
incidente e θ é o ângulo entre o campo elétrico E e a
direção de polarização do filtro. A intensidade luminosa,
a uma distância d de uma fonte que emite luz polarizada,
www.soexatas.com
NOTE E ADOTE
Índice de refração do ar = 1
Índice de refração da água = 1,3
Lei de Snell: v1 / v 2 = senθ1 / senθ2
Ângulo θ
sen θ
tg θ
Página 11
30º
40º
42º
53º
60º
0,50
0,64
0,67
0,80
0,87
4. (Fuvest 2010) Luz proveniente de uma lâmpada de
vapor de mercúrio incide perpendicularmente em uma das
o
o
o
faces de um prisma de vidro de ângulos 30 , 60 e 90 ,
imerso no ar, como mostra a figura a seguir.
0,58
0,84
0,90
1,33
1,73
3. (Unicamp 2010) Há atualmente um grande interesse no
desenvolvimento de materiais artificiais, conhecidos como
metamateriais, que têm propriedades físicas não
convencionais. Este é o caso de metamateriais que
apresentam índice de refração negativo, em contraste com
materiais convencionais que têm índice de refração
positivo. Essa propriedade não usual pode ser aplicada na
camuflagem de objetos e no desenvolvimento de lentes
especiais.
a) Na figura a seguir é representado um raio de luz A que se
propaga em um material convencional (Meio 1) com
índice de refração n1 = 1,8 e incide no Meio 2 formando
um ângulo θ1 = 30° com a normal. Um dos raios B, C, D
ou E apresenta uma trajetória que não seria possível em
um material convencional e que ocorre quando o Meio 2
é um metamaterial com índice de refração negativo.
Identifique este raio e calcule o módulo do índice de
refração do Meio 2, n2, neste caso, utilizando a lei de
Snell na forma:
n1 senθ1 = n2 senθ2 . Se necessário use
2 = 1,4 e 3 = 1,7.
b) O índice de refração de um meio material, n, é definido
pela razão entre as velocidades da luz no vácuo e no
meio. A velocidade da luz em um material é dada por
v=
1
, em que ε é a permissividade elétrica e μ é a
εμ
permeabilidade magnética do material. Calcule o índice de
refração de um material que tenha
ε = 2,0x10 −11
C2
N.m2
da luz no vácuo é
8
c = 3,0×10 m/s.
e µ = 1,25x10 −6
www.soexatas.com
N.s2
C2
A radiação atravessa o vidro e atinge um anteparo.
Devido ao fenômeno de refração, o prisma separa as
diferentes cores que compõem a luz da lâmpada de
mercúrio e observam-se, no anteparo, linhas de cor violeta,
azul, verde e amarela. Os valores do índice de refração n do
vidro para as diferentes cores estão dados adiante.
a) Calcule o desvio angular α, em relação a direção de
incidência, do raio de cor violeta que sai do prisma.
b) Desenhe, na figura da página de respostas, o raio de cor
violeta que sai do prisma.
c) Indique, na representação do anteparo na folha de
respostas, a correspondência entre as posições das linhas
L1, L2, L3 e L4 e as cores do espectro do mercúrio.
NOTE E ADOTE:
θ (graus)
senθ
Cor
N (vidro)
60
0,866
Violeta
1,532
50
0,766
Azul
1,528
40
0,643
Verde
1,519
30
0,500
amarelo
1,515
n =1 para qualquer
lei de Snell:
n1 senθ1 = n2 senθ2
comprimento de onda no ar.
b)
. A velocidade
Página 12
c)
5. (Fuvest 2009) Dois sistemas óticos, D1 e D2, são
utilizados para analisar
isar uma lâmina de tecido biológico a
partir de direções diferentes. Em uma análise, a luz
fluorescente, emitida por um indicador incorporado a uma
pequena estrutura, presente no tecido, é captada,
simultaneamente, pelos dois sistemas, ao longo das
direções tracejadas. Levando-se
se em conta o desvio da luz
pela refração, dentre as posições indicadas, aquela que
poderia corresponder à localização real dessa estrutura no
tecido é:
Suponha que o tecido biológico seja transparente à luz e
tenha índice de refração
ão uniforme, semelhante ao da água.
a) A
b) B
c) C
d) D
e) E
6. (Unesp 2008) Um objeto O é colocado frente a um corpo
com superfície esférica e uma imagem I desse objeto é
criada a uma distância de 14 cm do vértice V da superfície,
como ilustrado na figura.
°
O ângulo de incidência θi é 30 e θr é um ângulo que
permite a aproximação sen θr = tg θr. Determine o
tamanho da imagem I, considerando oíndice de refração do
vidro como sendo 1,7 e do ar como 1,0.
www.soexatas.com
7. (Unicamp 2008) A informação digital de um CD é
armazenada em uma camada de gravação que reside
abaixo de uma camada protetora, composta por um
plástico de 1,2 mm de espessura. A leitura da informação é
feita através de um feixe de laser que passa através de uma
lente convergente e da camada protetora para
p
ser
focalizado na camada de gravação, conforme representa a
figura a seguir. Nessa configuração, a área coberta pelo
feixe na superfície do CD é relativamente grande, reduzindo
os distúrbios causados por riscos na superfície.
a) Considere que o material
ial da camada de proteção tem
índice de refração n = 1,5, e que o ângulo de incidência
°
do feixe é de 30 em relação ao eixo normal à superfície
do CD. Usando a Lei de Snell, n1senθ1 = n2senθ2, calcule o
raio R do feixe na superfície do CD. Considere R = 0 no
ponto de leitura.
b) Durante a leitura, a velocidade angular de rotação do CD
varia conforme a distância do sistema ótico de leitura em
relação ao eixo de rotação. Isso é necessário para que a
velocidade linear do ponto de leitura seja constante.
Qual deve
eve ser a razão entre a velocidade angular de
rotação do CD quando o sistema ótico está na parte
central, de raio r1 = 2,0 cm e a velocidade angular de
rotação do CD quando o mesmo está na parte externa,
de raio r2 = 10 cm?
Página 13