1. (Ufg 2013) Baseado nas propriedades ondulatórias

MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
1. (Ufg 2013) Baseado nas propriedades ondulatórias de transmissão e reflexão, as
ondas de ultrassom podem ser empregadas para medir a espessura de vasos sanguíneos.
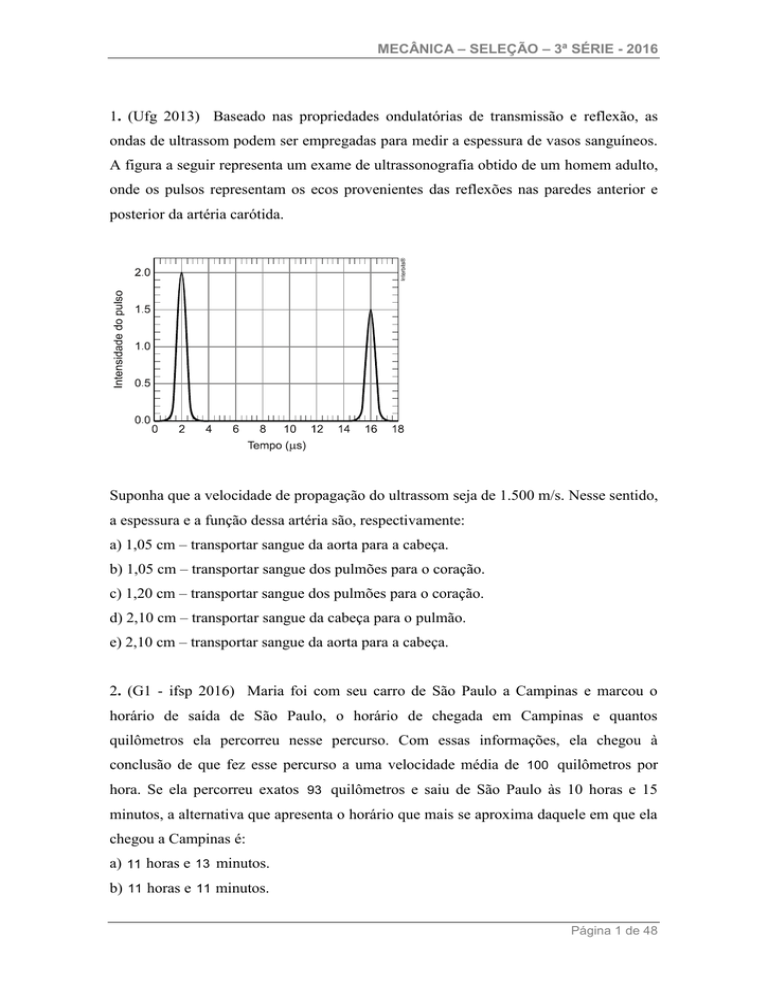
A figura a seguir representa um exame de ultrassonografia obtido de um homem adulto,
onde os pulsos representam os ecos provenientes das reflexões nas paredes anterior e
posterior da artéria carótida.
Suponha que a velocidade de propagação do ultrassom seja de 1.500 m/s. Nesse sentido,
a espessura e a função dessa artéria são, respectivamente:
a) 1,05 cm – transportar sangue da aorta para a cabeça.
b) 1,05 cm – transportar sangue dos pulmões para o coração.
c) 1,20 cm – transportar sangue dos pulmões para o coração.
d) 2,10 cm – transportar sangue da cabeça para o pulmão.
e) 2,10 cm – transportar sangue da aorta para a cabeça.
2. (G1 - ifsp 2016) Maria foi com seu carro de São Paulo a Campinas e marcou o
horário de saída de São Paulo, o horário de chegada em Campinas e quantos
quilômetros ela percorreu nesse percurso. Com essas informações, ela chegou à
conclusão de que fez esse percurso a uma velocidade média de 100 quilômetros por
hora. Se ela percorreu exatos 93 quilômetros e saiu de São Paulo às 10 horas e 15
minutos, a alternativa que apresenta o horário que mais se aproxima daquele em que ela
chegou a Campinas é:
a) 11 horas e 13 minutos.
b) 11 horas e 11 minutos.
Página 1 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
c) 11 horas e 09 minutos.
d) 11 horas e 07 minutos.
e) 11 horas e 05 minutos.
3. (Unesp 2016) Em uma viagem de carro com sua família, um garoto colocou em
prática o que havia aprendido nas aulas de física. Quando seu pai ultrapassou um
caminhão em um trecho reto da estrada, ele calculou a velocidade do caminhão
ultrapassado utilizando um cronômetro.
O garoto acionou o cronômetro quando seu pai alinhou a frente do carro com a traseira
do caminhão e o desligou no instante em que a ultrapassagem terminou, com a traseira
do carro alinhada com a frente do caminhão, obtendo 8,5 s para o tempo de
ultrapassagem.
Em seguida, considerando a informação contida na figura e sabendo que o comprimento
do carro era 4m e que a velocidade do carro permaneceu constante e igual a 30 m / s,
ele calculou a velocidade média do caminhão, durante a ultrapassagem, obtendo
corretamente o valor
a) 24 m / s.
b) 21m / s.
c) 22 m / s.
Página 2 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
d) 26 m / s.
e) 28 m / s.
4. (Unicamp 2016) A demanda por trens de alta velocidade tem crescido em todo o
mundo. Uma preocupação importante no projeto desses trens é o conforto dos
passageiros durante a aceleração. Sendo assim, considere que, em uma viagem de trem
de alta velocidade, a aceleração experimentada pelos passageiros foi limitada a
amax  0,09g, onde g  10 m / s2 é a aceleração da gravidade. Se o trem acelera a partir
do repouso com aceleração constante igual a amax , a distância mínima percorrida pelo
trem para atingir uma velocidade de 1080 km / h corresponde a
a) 10 km.
b) 20 km.
c) 50 km.
d) 100 km.
5. (Espcex (Aman) 2016) Um móvel descreve um movimento retilíneo uniformemente
acelerado. Ele parte da posição inicial igual a 40 m com uma velocidade de 30 m / s, no
sentido contrário à orientação positiva da trajetória, e a sua aceleração é de 10 m / s2 no
sentido positivo da trajetória. A posição do móvel no instante 4s é
a) 0 m
b) 40 m
c) 80 m
d) 100 m
e) 240 m
6. (G1 - cftmg 2016) Um objeto é lançado para baixo, na vertical, do alto de um prédio
de 15 m de altura em relação ao solo. Desprezando-se a resistência do ar e sabendo-se
que ele chega ao solo com uma velocidade de 20 m / s, a velocidade de lançamento, em
m / s, é dada por
a) 10.
b) 15.
Página 3 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
c) 20.
d) 25.
7. (Unicamp 2016) Anemômetros são instrumentos usados para medir a velocidade do
vento. A sua construção mais conhecida é a proposta por Robinson em 1846, que
consiste em um rotor com quatro conchas hemisféricas presas por hastes, conforme
figura abaixo. Em um anemômetro de Robinson ideal, a velocidade do vento é dada pela
velocidade linear das conchas. Um anemômetro em que a distância entre as conchas e o
centro de rotação é r  25 cm, em um dia cuja velocidade do vento é v  18 km / h, teria
uma frequência de rotação de
Se necessário, considere π  3.
a) 3 rpm.
b) 200 rpm.
c) 720 rpm.
d) 1200 rpm.
8. (Uerj 2016) Considere um patinador X que colide elasticamente com a parede P de
uma sala. Os diagramas abaixo mostram segmentos orientados indicando as possíveis
forças que agem no patinador e na parede, durante e após a colisão. Note que segmento
nulo indica força nula.
Página 4 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
Supondo desprezível qualquer atrito, o diagrama que melhor representa essas forças é
designado por:
a) I
b) II
c) III
d) IV
9. (Fmp 2016) Um helicóptero transporta, preso por uma corda, um pacote de massa
100 kg. O helicóptero está subindo com aceleração constante vertical e para cima de
0,5 m s2 .
Se a aceleração da gravidade no local vale 10 m s2 , a tração na corda, em
newtons, que sustenta o peso vale
a) 1.500
b) 1.050
c) 500
d) 1.000
e) 950
10. (Puccamp 2016) Para se calcular o coeficiente de atrito dinâmico entre uma moeda
e uma chapa de fórmica, a moeda foi colocada para deslizar pela chapa, colocada em
um ângulo de 37 com a horizontal.
Foi possível medir que a moeda, partindo do repouso, deslizou 2,0 m em um intervalo
de tempo de 1,0 s, em movimento uniformemente variado.
Adote g  10 m s2 , sen 37  0,60 e cos 37  0,80.
Nessas condições, o coeficiente de atrito dinâmico entre as superfícies vale
Página 5 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
a) 0,15.
b) 0,20.
c) 0,25.
d) 0,30.
e) 0,40.
11. (Acafe 2016) Um homem foi ao mercado comprar 2 kg de arroz, 1kg de feijão e
2 kg de açúcar. Quando saiu do caixa utilizou uma barra de PVC para facilitar no
transporte da sacola (figura 1). Quando chegou em casa reclamou para a mulher que
ficou cansado, pois a sacola estava pesada. Tentando ajudar o marido, a esposa
comentou que ele deveria na próxima vez trazer a sacola com as alças nas extremidades
da barra de PVC (figura 2), pois assim faria menos força. Na semana seguinte, o homem
foi ao mercado e comprou os mesmos produtos e carregou a sacola como a esposa havia
aconselhado.
A alternativa correta sobre a conclusão do homem é:
a) Minha esposa está certa, pois a sacola continua com o mesmo peso da semana
passada, no entanto, eu estou fazendo menos força para suportá-la.
b) Minha esposa está errada, pois a sacola continua com o mesmo peso da semana
passada e eu continuo fazendo a mesma força para suportá-la.
c) Minha esposa está certa, pois estou fazendo menos força para suportar a sacola
porque ela ficou mais leve.
d) Minha esposa está errada, pois a sacola ficou mais pesada do que a da semana
passada e eu estou fazendo mais força para suportá-la.
Página 6 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
12. (G1 - ifsp 2016)
Complete o quadro a seguir que explica as principais
transformações de energia que ocorre em cada tipo de usina.
Energia
Energia
inicial
final
Hidrelétrica
I
Elétrica
Termoelétrica
II
Elétrica
Termonuclear
III
Elétrica
Eólica
IV
Elétrica
Fotovoltaica
V
Elétrica
Tipos de usinas
A alternativa correta que completa a coluna energia inicial é:
a) I - térmica; II - térmica; III - térmica; IV - mecânica; V - luminosa.
b) I - mecânica; II - mecânica; III - luminosa; IV - mecânica; V - mecânica.
c) I - térmica; II - luminosa; III - luminosa; IV - mecânica; V - térmica.
d) I - mecânica; II - térmica; III - térmica; IV - mecânica; V - luminosa.
e) I - luminosa; II - térmica; III - mecânica; IV - mecânica; V - térmica.
13. (G1 - cftmg 2016) Dois blocos A e B de mesmas dimensões e materiais diferentes
são pendurados no teto por fios de mesmo comprimento e mergulhados em uma cuba
cheia de água, conforme a figura abaixo. Cortando-se os fios, observa-se que A
permanece na mesma posição dentro da água, enquanto B vai para o fundo.
Com relação a esse fato, pode-se afirmar que a densidade do bloco
a) B é menor que a de A.
b) A é menor que a de B.
c) A é menor que a da água.
Página 7 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
d) B é menor que a da água.
14. (Pucpr 2016) Um foguete, de massa M, encontra-se no espaço e na ausência de
gravidade com uma velocidade (V0 ) de 3000 km h em relação a um observador na
Terra, conforme ilustra a figura a seguir. Num dado momento da viagem, o estágio, cuja
massa representa 75% da massa do foguete, é desacoplado da cápsula. Devido a essa
separação, a cápsula do foguete passa a viajar 800 km h mais rápido que o estágio.
Qual a velocidade da cápsula do foguete, em relação a um observador na Terra, após a
separação do estágio?
a) 3000 km h.
b) 3200 km h.
c) 3400 km h.
d) 3600 km h.
e) 3800 km h.
15. (Pucrs 2016) Para responder à questão, analise a situação a seguir.
Duas esferas – A e B – de massas respectivamente iguais a 3 kg e 2 kg estão em
movimento unidimensional sobre um plano horizontal perfeitamente liso, como mostra
a figura 1.
Página 8 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
Inicialmente as esferas se movimentam em sentidos opostos, colidindo no instante t1. A
figura 2 representa a evolução das velocidades em função do tempo para essas esferas
imediatamente antes e após a colisão mecânica.
Sobre o sistema formado pelas esferas A e B, é correto afirmar:
a) Há conservação da energia cinética do sistema durante a colisão.
b) Há dissipação de energia mecânica do sistema durante a colisão.
c) A quantidade de movimento total do sistema formado varia durante a colisão.
d) A velocidade relativa de afastamento dos corpos após a colisão é diferente de zero.
e) A velocidade relativa entre as esferas antes da colisão é inferior à velocidade relativa
entre elas após colidirem.
16. (Uerj 2016) Em um pêndulo, um fio de massa desprezível sustenta uma pequena
esfera magnetizada de massa igual a 0,01kg. O sistema encontra-se em estado de
equilíbrio, com o fio de sustentação em uma direção perpendicular ao solo.
Um ímã, ao ser aproximado do sistema, exerce uma força horizontal sobre a esfera, e o
pêndulo alcança um novo estado de equilíbrio, com o fio de sustentação formando um
ângulo de 45 com a direção inicial.
Admitindo a aceleração da gravidade igual a 10 m  s2 , a magnitude dessa força, em
newtons, é igual a:
a) 0,1
b) 0,2
Página 9 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
c) 1,0
d) 2,0
17. (Epcar (Afa) 2016) Dois móveis, A e B, partindo juntos de uma mesma posição,
porém com velocidades diferentes, que variam conforme o gráfico abaixo, irão se
encontrar novamente em um determinado instante.
Considerando que os intervalos de tempo t1  t0 , t2  t1, t3  t2, t 4  t3 e t5  t 4 são todos
iguais, os móveis A e B novamente se encontrarão no instante
a) t 4
b) t 5
c) t 2
d) t 3
18. (Uerj 2015) Em uma pista de competição, quatro carrinhos elétricos, numerados de
I a IV, são movimentados de acordo com o gráfico v  t a seguir.
Página 10 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
O carrinho que percorreu a maior distância em 4 segundos tem a seguinte numeração:
a) I
b) II
c) III
d) IV
19. (Unesp 2015) A fotografia mostra um avião bombardeiro norte-americano B52
despejando bombas sobre determinada cidade no Vietnã do Norte, em dezembro de
1972.
Durante essa operação, o avião bombardeiro sobrevoou, horizontalmente e com
velocidade vetorial constante, a região atacada, enquanto abandonava as bombas que, na
fotografia tirada de outro avião em repouso em relação ao bombardeiro, aparecem
alinhadas verticalmente sob ele, durante a queda. Desprezando a resistência do ar e a
atuação de forças horizontais sobre as bombas, é correto afirmar que:
a) no referencial em repouso sobre a superfície da Terra, cada bomba percorreu uma
trajetória parabólica diferente.
b) no referencial em repouso sobre a superfície da Terra, as bombas estavam em
movimento retilíneo acelerado.
c) no referencial do avião bombardeiro, a trajetória de cada bomba é representada por
um arco de parábola.
d) enquanto caíam, as bombas estavam todas em repouso, uma em relação às outras.
e) as bombas atingiram um mesmo ponto sobre a superfície da Terra, uma vez que
caíram verticalmente.
Página 11 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
20. (Udesc 2015) Deixa-se cair um objeto de massa 500 g de uma altura de 5m acima
do solo. Assinale a alternativa que representa a velocidade do objeto, imediatamente,
antes de tocar o solo, desprezando-se a resistência do ar.
a) 10m / s
b) 7,0m / s
c) 5,0m / s
d) 15m / s
e) 2,5m / s
21. (Unesp 2015) A figura representa, de forma simplificada, parte de um sistema de
engrenagens que tem a função de fazer girar duas hélices, H1 e H2 . Um eixo ligado a um
motor gira com velocidade angular constante e nele estão presas duas engrenagens, A e
B. Esse eixo pode se movimentar horizontalmente assumindo a posição 1 ou 2. Na
posição 1, a engrenagem B acopla-se à engrenagem C e, na posição 2, a engrenagem
A acopla-se à engrenagem D. Com as engrenagens B e C acopladas, a hélice H1 gira
com velocidade angular constante ω1 e, com as engrenagens A e D acopladas, a hélice
H2 gira com velocidade angular constante ω2 .
Página 12 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
Considere rA , rB, rC , e rD, os raios das engrenagens A, B, C e D, respectivamente.
Sabendo que rB  2  rA e que rC  rD , é correto afirmar que a relação
ω1
é igual a
ω2
a) 1,0.
b) 0,2.
c) 0,5.
d) 2,0.
e) 2,2.
22. (Espcex (Aman) 2015) Uma pessoa de massa igual a 80 kg está dentro de um
elevador sobre uma balança calibrada que indica o peso em newtons, conforme desenho
abaixo. Quando o elevador está acelerado para cima com uma aceleração constante de
intensidade a  2,0 m / s2, a pessoa observa que a balança indica o valor de
Dado: intensidade da aceleração da gravidade g  10 m / s2
a) 160 N
b) 640 N
c) 800 N
d) 960 N
e) 1600 N
23. (Ifsul 2015) O sistema abaixo está em equilíbrio.
Página 13 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
A razão
a)
2
5
b)
2
3
c)
3
2
d)
5
2
T1
entre as intensidades das trações nos fios ideais 1 e 2 vale
T2
24. (Ufpr 2015) Um bloco B de massa 400g está apoiado sobre um bloco A de massa
800g, o qual está sobre uma superfície horizontal. Os dois blocos estão unidos por uma
corda inextensível e sem massa, que passa por uma polia presa na parede, conforme
ilustra abaixo. O coeficiente de atrito cinético entre os dois blocos e entre o bloco A e a
superfície horizontal é o mesmo e vale 0,35. Considerando a aceleração da gravidade
igual a 10m / s2 e desprezando a massa da polia, assinale a alternativa correta para o
módulo da força F necessária para que os dois blocos se movam com velocidade
constante.
a) 1,4N.
b) 4,2N.
Página 14 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
c) 7,0N.
d) 8,5N.
e) 9,3N.
25. (G1 - cps 2015) A apresentação de motociclistas dentro do globo da morte é sempre
um momento empolgante de uma sessão de circo, pois ao atingir o ponto mais alto do
globo, eles ficam de ponta cabeça. Para que, nesse momento, o motociclista não caia, é
necessário que ele esteja a uma velocidade mínima (v) que se relaciona com o raio do
globo (R) e a aceleração da gravidade (g) pela expressão: v  R  g, com R dado em
metros.
Considere que no ponto mais alto de um globo da morte, um motociclista não caiu, pois
estava com a velocidade mínima de 27km h.
Assim sendo, o raio do globo é, aproximadamente, em metros,
Adote g  10m / s2
a) 5,6.
b) 6,3.
c) 7,5.
d) 8,2.
e) 9,8.
26. (Pucrj 2015) Um elevador de 500 kg deve subir uma carga de 2,5 toneladas a uma
Página 15 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
altura de 20 metros, em um tempo inferior a 25 segundos. Qual deve ser a potência
média mínima do motor do elevador, em kW ?
Dado: g  10 m / s2
a) 20
b) 16
c) 24
d) 38
e) 15
27. (Uerj 2015) Um carro, em um trecho retilíneo da estrada na qual trafegava, colidiu
frontalmente com um poste. O motorista informou um determinado valor para a
velocidade de seu veículo no momento do acidente. O perito de uma seguradora apurou,
no entanto, que a velocidade correspondia a exatamente o dobro do valor informado
pelo motorista.
Considere Ec1 a energia cinética do veículo calculada com a velocidade informada pelo
motorista e Ec 2 aquela calculada com o valor apurado pelo perito.
A razão
a)
1
2
b)
1
4
Ec1
corresponde a:
Ec 2
c) 1
d) 2
28. (Pucmg 2015)
A densidade do óleo de soja usado na alimentação é de
aproximadamente 0,80 g / cm3 . O número de recipientes com o volume de 1litro que se
podem encher com 80 kg desse óleo é de:
a) 100
b) 20
c) 500
d) 50
Página 16 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
29. (Epcar (Afa) 2015) A figura abaixo representa um macaco hidráulico constituído de
dois pistões A e B de raios RA  60 cm e RB  240 cm, respectivamente. Esse
dispositivo será utilizado para elevar a uma altura de 2 m, em relação à posição inicial,
um veículo de massa igual a 1 tonelada devido à aplicação de uma força F. Despreze as
massas dos pistões, todos os atritos e considere que o líquido seja incompressível.
Nessas condições, o fator de multiplicação de força deste macaco hidráulico e o
trabalho, em joules, realizado pela força F, aplicada sobre o pistão de menor área, ao
levantar o veículo bem lentamente e com velocidade constante, são, respectivamente,
a) 4 e 2,0  104
b) 4 e 5,0  103
c) 16 e 2,0  104
d) 16 e 1,25  103
30. (Imed 2015)
Dois carros de mesma massa sofrem uma colisão frontal.
Imediatamente, antes da colisão, o primeiro carro viajava a 72 km h no sentido norte de
uma estrada retilínea, enquanto o segundo carro viajava na contramão da mesma estrada
com velocidade igual a 36 km h, no sentido sul. Considere que a colisão foi
perfeitamente inelástica. Qual é a velocidade final dos carros imediatamente após essa
colisão?
a) 5 m s para o norte.
b) 5 m s para o sul.
c) 10 m s para o norte.
d) 10 m s para o sul.
Página 17 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
e) 30 m s para o norte.
31. (G1 - cps 2015) A Op Art ou “arte óptica” é um segmento do Cubismo abstrato que
valoriza a ideia de mais visualização e menos expressão. É por esse motivo que alguns
artistas dessa vertente do Cubismo escolheram o móbile como base de sua arte.
No móbile representado, considere que os “passarinhos” tenham a mesma massa e que
as barras horizontais e os fios tenham massas desprezíveis.
Para que o móbile permaneça equilibrado, conforme a figura, a barra maior que sustenta
todo o conjunto deve receber um fio que a pendure, atado ao ponto numerado por
a) 1.
b) 2.
c) 3.
d) 4.
e) 5.
32. (Enem 2015) Em um experimento, um professor levou para a sala de aula um saco
de arroz, um pedaço de madeira triangular e uma barra de ferro cilíndrica e homogênea.
Ele propôs que fizessem a medição da massa da barra utilizando esses objetos. Para
isso, os alunos fizeram marcações na barra, dividindo-a em oito partes iguais, e em
seguida apoiaram-na sobre a base triangular, com o saco de arroz pendurado em uma de
suas extremidades, até atingir a situação de equilíbrio.
Página 18 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
Nessa situação, qual foi a massa da barra obtida pelos alunos?
a) 3,00 kg
b) 3,75 kg
c) 5,00 kg
d) 6,00 kg
e) 15,00 kg
33. (Uece 2014) Considere um cubo imerso em água, conforme a figura a seguir.
No ponto destacado de uma das faces desse cubo, há uma força devido à pressão
hidrostática exercida pela água. Assinale o vetor que melhor representa essa força.
a) FI
b) FII
c) FIII
d) FIV
34. (Fmp 2014) Uma prensa hidráulica é composta por dois reservatórios: um cilíndrico
e outro em forma de prisma com base quadrada. O diâmetro do êmbolo do reservatório
cilíndrico tem a mesma medida que o lado do êmbolo do reservatório prismático. Esses
Página 19 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
êmbolos são extremamente leves e podem deslocar-se para cima ou para baixo, sem
atrito, e perfeitamente ajustados às paredes dos reservatórios.
Sobre o êmbolo cilíndrico está um corpo de peso P.
A força que deve ser aplicada no êmbolo quadrado para elevar esse corpo deve ter
intensidade mínima igual a
a)
P
π
b)
2P
π
c)
4P
π
d)
π P
2
e)
π P
4
35. (Espcex (Aman) 2014) Um bloco de massa M=180 g está sobre urna superfície
horizontal sem atrito, e prende-se a extremidade de uma mola ideal de massa
desprezível e constante elástica igual a 2  103 N / m. A outra extremidade da mola está
presa a um suporte fixo, conforme mostra o desenho. Inicialmente o bloco se encontra
em repouso e a mola no seu comprimento natural, Isto é, sem deformação.
Página 20 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
Um projétil de massa m=20 g é disparado horizontalmente contra o bloco, que é de fácil
penetração. Ele atinge o bloco no centro de sua face, com velocidade de v=200 m/s.
Devido ao choque, o projétil aloja-se no interior do bloco. Desprezando a resistência do
ar, a compressão máxima da mola é de:
a) 10,0 cm
b) 12,0 cm
c) 15,0 cm
d) 20,0 cm
e) 30,0 cm
36. (Acafe 2014) O tratamento de tração é a aplicação de uma força de tração sobre
uma parte do corpo. A tração ainda é usada principalmente como uma prescrição em
curto prazo até que outras modalidades, como a fixação externa ou interna, sejam
possíveis. Isso reduz o risco da síndrome do desuso. Seja um paciente de massa 50 kg
submetido a um tratamento de tração como na figura abaixo, que está deitado em uma
cama onde o coeficiente de atrito entre a mesma e o paciente é μ  0,26.
Sabendo-se que o ângulo entre a força de tração e a horizontal é 30°, a alternativa
correta que apresenta a máxima massa, em kg, que deve ser utilizada para produzir tal
força de tração sem que o paciente se desloque em cima da cama é:
a) 25
b) 13
c) 10
d) 50
Página 21 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
37. (Unesp 2013) Um garçom deve levar um copo com água apoiado em uma bandeja
plana e mantida na horizontal, sem deixar que o copo escorregue em relação à bandeja e
sem que a água transborde do copo.
O copo, com massa total de 0,4 kg, parte do repouso e descreve um movimento retilíneo
e acelerado em relação ao solo, em um plano horizontal e com aceleração constante.
Em um intervalo de tempo de 0,8 s, o garçom move o copo por uma distância de 1,6 m.
Desprezando a resistência do ar, o módulo da força de atrito devido à interação com a
bandeja, em newtons, que atua sobre o copo nesse intervalo de tempo é igual a
a) 2.
b) 3.
c) 5.
d) 1.
e) 4.
38. (Ufrgs 2013) A figura apresenta esquematicamente o sistema de transmissão de
uma bicicleta convencional.
Página 22 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
Na bicicleta, a coroa A conecta-se à catraca B através da correia P. Por sua vez, B é
ligada à roda traseira R, girando com ela quando o ciclista está pedalando.
Nesta situação, supondo que a bicicleta se move sem deslizar, as magnitudes das
velocidades angulares, ωA , ωB e ωR , são tais que
a) ωA  ωB  ωR .
b) ωA  ωB  ωR .
c) ωA  ωB  ωR .
d) ωA  ωB  ωR .
e) ωA  ωB  ωR .
39. (Upe 2013) Suponha um bloco de massa m = 2 kg inicialmente em repouso sobre
um plano horizontal sem atrito. Uma força F = 16 N é aplicada sobre o bloco, conforme
mostra a figura a seguir.
Qual é a intensidade da reação normal do plano de apoio e a aceleração do bloco,
respectivamente, sabendo-se que sen 60° = 0,85, cos 60° = 0,50 e g = 10 m/s2?
a) 6,4 N e 4 m/s2
b) 13, 6 N e 4 m/s2
c) 20,0 N e 8 m/s2
d) 16,0 N e 8 m/s2
e) 8,00 N e 8 m/s2
40. (Pucrj 2013) Sobre uma superfície sem atrito, há um bloco de massa m1 = 4,0 kg
sobre o qual está apoiado um bloco menor de massa m2 = 1,0 kg. Uma corda puxa o
bloco menor com uma força horizontal F de módulo 10 N, como mostrado na figura
abaixo, e observa-se que nesta situação os dois blocos movem-se juntos.
Página 23 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
A força de atrito existente entre as superfícies dos blocos vale em Newtons:
a) 10
b) 2,0
c) 40
d) 13
e) 8,0
41. (Unesp 2013) A figura representa, de forma simplificada, o autódromo de Tarumã,
localizado na cidade de Viamão, na Grande Porto Alegre. Em um evento comemorativo,
três veículos de diferentes categorias do automobilismo, um kart (K), um fórmula 1 (F)
e um stock-car (S), passam por diferentes curvas do circuito, com velocidades escalares
iguais e constantes.
As tabelas 1 e 2 indicam, respectivamente e de forma comparativa, as massas de cada
veículo e os raios de curvatura das curvas representadas na figura, nas posições onde se
encontram os veículos.
Página 24 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
TABELA 1
TABELA 2
Veículo
Massa
Curva
Raio
kart
M
Tala Larga 2R
fórmula 1 3M
do Laço
R
stock-car
Um
3R
6M
Sendo FK, FF e FS os módulos das forças resultantes centrípetas que atuam em cada um
dos veículos nas posições em que eles se encontram na figura, é correto afirmar que
a) FS < FK < FF.
b) FK < FS < FF.
c) FK < FF < FS.
d) FF < FS < FK.
e) FS < FF < FK.
42. (Unesp 2013)
A figura ilustra um brinquedo oferecido por alguns parques,
conhecido por tirolesa, no qual uma pessoa desce de determinada altura segurando-se
em uma roldana apoiada numa corda tensionada. Em determinado ponto do percurso, a
pessoa se solta e cai na água de um lago.
Considere que uma pessoa de 50 kg parta do repouso no ponto A e desça até o ponto B
segurando-se na roldana, e que nesse trajeto tenha havido perda de 36% da energia
mecânica do sistema, devido ao atrito entre a roldana e a corda. No ponto B ela se solta,
atingindo o ponto C na superfície da água. Em seu movimento, o centro de massa da
pessoa sofre o desnível vertical de 5 m mostrado na figura.
Desprezando a resistência do ar e a massa da roldana, e adotando g = 10 m/s2, pode-se
afirmar que a pessoa atinge o ponto C com uma velocidade, em m/s, de módulo igual a
Página 25 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
a) 8.
b) 10.
c) 6.
d) 12.
e) 4.
43. (Uerj 2013) Observe, na figura a seguir, a representa玢o de uma prensa hidr醬lica,
na qual as for鏰s F1 e F2 atuam, respectivamente, sobre os 阭bolos dos cilindros I e II.
Admita que os cilindros estejam totalmente preenchidos por um l韖uido.
O volume do cilindro II ? igual a quatro vezes o volume do cilindro I, cuja altura ? o
triplo da altura do cilindro II.
A raz鉶
F2
entre as intensidades das for鏰s, quando o sistema est? em equil韇rio,
F1
corresponde a:
a) 12
b) 6
c) 3
d) 2
44. (Enem PPL 2013) Retirar a roda de um carro é uma tarefa facilitada por algumas
características da ferramenta utilizada, habitualmente denominada chave de roda. As
figuras representam alguns modelos de chaves de roda:
Página 26 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
Em condições usuais, qual desses modelos permite a retirada da roda com mais
facilidade?
a) 1, em função de o momento da força ser menor.
b) 1, em função da ação de um binário de forças.
c) 2, em função de o braço da força aplicada ser maior.
d) 3, em função de o braço da força aplicada poder variar.
e) 3, em função de o momento da força produzida ser maior.
Página 27 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
Gabarito:
Resposta da questão 1: [A]
[Resposta do ponto de vista da disciplina de Biologia]
As artérias carótidas transportam sangue arterial da aorta para a cabeça.
[Resposta do ponto de vista da disciplina de Física]
Do gráfico, a diferença de tempo entre as duas recepções é:
Δt  16  2  14 μs  14  106 s.
A distância percorrida (d) nesse intervalo de tempo é igual a duas vezes a espessura (e)
da artéria. Assim:
d  v Δt  2 e  v Δt  e 
v Δt 1500  14  106

 1,05  102 m 
2
2
e  1,05 cm.
Resposta da questão 2: [B]
Dados: ΔS  93km; vm  100km/h
Δt 
ΔS 93

h  0,93h  0,93  60min   55,8min  Δt  56min.
vm 100
Horário de chegada:
t  10h e 15min  56 min  11h e 11min.
Resposta da questão 3: [D]
Dados: v A  30 m/s; Δt  8s; LA  4m; LB  30m.
Em relação ao caminhão, a velocidade do carro (vrel ) e o deslocamento relativo durante
a ultrapassagem (ΔSrel ), são:
Página 28 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
vrel  v A  v C  vrel  30  v C .

ΔSrel  L A  LC  30  4  ΔSrel  34m.
v C  30  4 
 vrel 
ΔSrel
34
 30  v C 

Δt
8,5
v C  26m/s.
Resposta da questão 4:[C]
Dados: a max  0,09 g  0,09 10  0,9 m/s2; v0  0; v  1080 km/h  300 m/s.
A distância é mínima quando a aceleração escalar é máxima. Na equação de Torricelli:
v 2  v 02  2 amax dmin  dmin 
v 2  v 02 3002  02 90.000


 50.000 m 
2 amax
2  0,9
1,8
dmin  50 km.
Resposta da questão 5: [A]
Pelos dados do enunciado e pela função horária do espaço para um MRUV, temos que:
a  t2
2
10  16
S  40  30  4 
2
S  40  120  80
S0m
S  S0  v 0  t 
Resposta da questão 6: [A]
Dado: v  20m s; h  15m; g  10 m s2.
Aplicando a equação de Torricelli:
v 2  v 02  2gh  v 0 
v 2  2gh 
202  2  10  15 
100 
v 0  10 m s.
Resposta da questão 7: [B]
Página 29 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
Dados: v  18 km/h  5 m/s; r  25 cm  0,25 m; π  3.
v  2 πr f  f 
v
5
5
5


Hz 
 60 rpm 
2 π r 2  3  0,25 1,5
1,5
f  200 Hz.
Resposta da questão 8: [A]
Conforme descrito no enunciado, o patinador colide elasticamente com a parede. Disto,
podemos dizer que o patinador estará exercendo uma força na parede durante um certo
intervalo de tempo (ou um Impulso). Devido a isto, pelo Princípio da Ação e Reação, a
parede irá exercer uma força sobre o patinador de mesma intensidade, mesma direção e
com o sentido contrário.
Vale salientar que as duas forças só estarão atuando no patinador e na parede durante a
colisão.
Desta forma, analisando as alternativas,
[I] CORRETA.
[II] INCORRETA. As intensidades das forças são iguais durante a colisão e após não
existe forças atuando nos corpos.
[III] INCORRETA. Vai contra o Princípio da Ação e Reação.
[IV] INCORRETA. Alternativa contraria a situação que de fato ocorre. Ver explicação.
Resposta da questão 9: [B]
Observando o diagrama de corpo livre para o sistema de corpos:
Página 30 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
Aplicando a segunda lei de Newton sobre o pacote:
FR  m  a
T mg  ma
T  m   g  a  T  100 kg  10  0,5 m / s2  T  1050 N
Resposta da questão 10: [C]
Analisando o proposto pelo enunciado, podemos desenhar o diagrama de forças que
atuam sobre o corpo.
Assim, analisando as forças, temos que:

FR  P  sen  37   Fat


P  cos  37   N
Pelos dados de deslocamento, podemos calcular a aceleração da moeda no tempo dado:
ΔS  v o  t 
2
a  t2
2
a  12
2
a  4 m s2
Diante disto, temos que:
Página 31 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
FR  P  sen  37   Fat
FR  P  sen  37   μ  N
FR  P  sen  37   μ  P  cos  37 
m  a  m  g  sen  37   μ  m  g  cos  37 
a  g  sen  37   μ  g  cos  37 
4  10  0,6  μ  10  0,8
μ  0,25
Resposta da questão 11: [B]
O peso da sacola de compras, tanto da figura 1 como da figura 2 são exatamente iguais,
pois o mesmo não é modificado pelo fato de segurar de forma diferente, portanto a
esposa está errada. Agora, a pressão aplicada no bastão é maior para a figura 1 em
relação à figura 2, e esta sim é capaz de se alterar devido à área de contato ser diferente
em ambas as posições, sendo a pressão dada pela razão entre a força e a área de contato,
quanto menor for a área de contato maior será a pressão.
Resposta da questão 12: [D]
As transformações estão descritas na tabela.
Energia
Energia
inicial
final
Hidrelétrica
I – Mecânica
Elétrica
Termoelétrica
II – Térmica
Elétrica
Termonuclear
III – Térmica
Elétrica
Eólica
IV – Mecânica
Elétrica
Fotovoltaica
V – Luminosa
Elétrica
Tipos de usinas
Resposta da questão 13: [B]
O bloco A continua na mesma posição: sua densidade é igual à da água;
O bloco B vai para o fundo: sua densidade é maior que a da água.
Assim:
Página 32 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
dA  dág

dB  dág

dA  dB
Resposta da questão 14: [D]
Pela conservação do momento linear, temos que:
Qfog.  Qest .  Qcap.
M  v fog.  mest.  v est.  mcap.  v cap.
Onde,
 v fog.  3000 km h

mest.  0,75  M

 v est.  v  800
m
 0,25  M
 cap.
v
 cap.  v
Assim,
3000  M   0,75  M   v  800    0,25  M  v
3000  0,75  v  600  0,25  v
v  3600 km h
Resposta da questão 15: [B]
Pela análise do gráfico, constata-se que os corpos andam juntos após o choque
(velocidade relativa de afastamento dos corpos depois do choque é igual a zero),
representando um choque perfeitamente inelástico. Neste caso, a energia cinética não é
conservada e existe a perda de parte da energia mecânica inicial sob a forma de calor
(energia dissipada) com aumento da energia interna e temperatura devido à deformação
sofrida no choque. Sendo assim, a única alternativa correta é da letra [B].
Resposta da questão 16: [A]
A figura mostra as forças que agem na esfera: peso, tração e força magnética.
Página 33 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
Como a esfera está em equilíbrio, pela regra da poligonal, as três forças devem fechar
um triângulo.
tg 45
F
 F  P tg 45  m g (1)  0,01(10) 
P
F  0,1 N.
Resposta da questão 17: [A]
O móvel B começa com maior velocidade em relação ao móvel A inicialmente e,
portanto como a distância percorrida representa a área sob a curva v  t, a área pintada
de amarelo representa a vantagem percorrida por B em relação à A até o momento t 2
quando as velocidades dos dois móveis passam a ser iguais (área A1), a partir do qual
com o móvel B desacelerando e o móvel A acelerando com o mesmo módulo. Como os
móveis acabam invertendo as velocidades, agora é o móvel A que começa a percorrer
Página 34 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
maior distância com o tempo e a área pintada de azul representa a vantagem de A em
relação à B (área A 2 ).
Para que os dois móveis se encontrem novamente estas áreas devem ser iguais, portanto
o encontro se dá no tempo t 4 .
Resposta da questão 18: [B]
No gráfico v  t, a distância percorrida é obtida pela ”área" entre a linha do gráfico e o
eixo dos tempos. Calculando cada uma delas:

 2  0,5 1
2  0,5

 1 2  0,5  1,25  2  3,75 m.
DI 
2
2





1,5  1 2
1 1

 1,5  1  0,5  2,5  1,5  4,5 m.
DII 
2
2





2 1
 2  1  1  2  3 m.
DIII 
2





D  3  0,5   0,5  11  0,75  0,75  1,5 m.
IV
2
2

Resposta da questão 19: [A]
Como o avião bombardeiro tem velocidade horizontal constante, as bombas que são
abandonadas têm essa mesma velocidade horizontal, por isso estão sempre abaixo dele.
No referencial do outro avião que segue trajetória paralela à do bombardeiro, o
movimento das bombas corresponde a uma queda livre, uma vez que a resistência do ar
pode ser desprezada. A figura mostra as trajetórias parabólicas das bombas B1, B2, B3 e
B4 abandonadas, respectivamente, dos pontos P1, P2 , P3 e P4 no referencial em repouso
sobre a superfície da Terra.
Página 35 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
Resposta da questão 20: [A]
Sabendo que se trata de uma queda livre (velocidade inicial v0 é nula), onde a altura
inicial é de 5 metros e a massa do corpo é de 0,5 kg, podemos resolver de duas formas
distintas.
1ª Solução – Queda Livre:
Utilizando a equação de Torricelli, temos que:
v 2  v 02  2  a  ΔS
Onde,
ag
ΔS  h
v0  0
Temos que,
v2  2  g  h
v 2  2  10  5
v  100
v  10 m s
2ª Solução – Conservação de Energia Mecânica:
Sabendo que inicialmente o corpo está em repouso, podemos dizer que:
Página 36 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
Em  Em
f
Ep  Ec
f
i
gi
m gh 
m  v2
2
v2  2  g  h
v  10 m s
Resposta da questão 21: [D]
Na posição 1:









rB  2 r A .
ωB  ωA 
vB
vB
 ωA 
 ωA  v B  2 ω A r A .
rB
2 rA
v C  vB  ωC rC  2 ωA rA .
ωC  ω1  ω1rC  2 ωA rA . (I)
Na posição 2:
 vD  v A  ω D rD  ωA rA .

 ω2  ωD .
 r r .
 C D
 ω2 rC  ωA rA . (II)
Dividindo membro a membro (I) por (II):
ω1 rC
ω2 rC

2 ωA rA
ωA rA

ω1
 2.
ω2
Resposta da questão 22: [D]
Entendendo que a balança do enunciado seja na verdade um dinamômetro, a leitura
indicada é a intensidade (FN) da força normal que a plataforma do dinamômetro aplica
nos pés da pessoa:
FN  P  m a  FN  800  80  2  
FN  960 N.
Resposta da questão 23: [D]
Página 37 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
Do diagrama abaixo, determinamos a força resultante para cada corpo:
Para o corpo 1:
T1  P1  T2
Para o corpo 2:
T2  P2
Então,
T1  P1  P2  T1  60  40  T1  100 N
T2  40 N
Logo, a razão
T1
será:
T2
T1 100 5


T2
40 2
Resposta da questão 24: [C]
Para que os dois blocos se movam com velocidade constante, basta que a força
resultante em cada um deles separadamente seja nula.
Analisando o Bloco B, temos que:
Página 38 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
Disto, para que a força resultante seja nula,
T  Fat
BA
 μ  mB  g
T  0,35  0,4  10
T  1,4 N
Analisando o Bloco A, temos que:
Note que a força de atrito entre o bloco A e o bloco B também deve ser considerada
neste caso.
Disto, para que a força resultante seja nula,
F  T  Fat
AS
 Fat
BA
F  1,4  0,35  mA  mB   g  1,4
F  1,4  0,35  1,2  10  1,4
F  7,0 N
Resposta da questão 25: [A]
Sabendo que 27km h 
15
m s, vem
2
15
 R  10  R  5,6 m.
2
Resposta da questão 26: [C]
Página 39 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
No caso, a potência mínima será dada por:
P
 500  2500  kg  10 m / s2  20 m
τ mgh

P
 24000 W  24 kW
Δt
Δt
25 s
Resposta da questão 27: [B]

m v2
Ec 1 

2

2

m 2 v 
Ec

 2
2

mv
 Ec 2  4
2

Ec 1 1
 .
Ec 2 4
2
Resposta da questão 28: [A]
Dados: d  0,8 g/cm3  0,8 kg/L; m  80 kg.
Calculando o volume ocupado por 80 kg de óleo:
d
m
m 80
 V 
V
d 0,8

V  100 L.
Como o volume de cada recipiente é 1 L, podem ser enchidos 100 recipientes.
Resposta da questão 29: [C]
Pelo princípio de Pascal, a pressão é transmitida integralmente por cada ponto do
líquido, isto é, a pressão no pistão A é igual à pressão no pistão B :
pA  pB
Usando a definição de pressão como a razão entre a força F e a área A, ficamos com:
FA
F
 B
A A AB
Fazendo a razão entre as forças e calculando as áreas dos pistões
Página 40 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
π   240 cm 
FB
A
F
F
 B  B 
 B  16
2
FA A A
FA
FA
π   60 cm 
2
Já o trabalho W realizado para erguer o automóvel é:
W  F  h  W  m  g  h  W  1000 kg  10 m / s2  2 m
W  2  104 J
Resposta da questão 30: [A]
Tem-se a seguinte situação.
Em uma colisão perfeitamente inelástica, os corpos permanecem juntos após a colisão.
Desta forma:
m1  v1i  m2  v2i  m1  v1f  m2  v2 f
Como,
v1f  v 2 f
m1  v1i  m2  v 2 i  m1  m2   v f
m   20   m   10   2  m  v f
2v  10
v  5m s
Assim,
Página 41 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
Resposta da questão 31: [C]
Quando suspensa, a barra maior sofrerá em cada extremidade uma tração de intensidade
igual à do triplo do peso de cada passarinho. Então, por simetria, ela deve receber um
fio que a pendure, atado ao seu ponto médio, ou seja, o ponto de número 3.
Resposta da questão 32: [E]
Na barra agem as três forças mostradas na figura: peso do saco arroz (Pa ), o peso da
barra (Pb ), agindo no centro de gravidade pois a barra é homogênea e a normal (N), no
ponto de apoio.
Adotando o polo no ponto de apoio, chamando de u o comprimento de cada divisão e
fazendo o somatório dos momentos, temos:
MP  MP
b
a
 m b g  u   m a g 3 u   m b  3 5  
m b  15 kg.
Resposta da questão 33: [A]
A força que provoca pressão é perpendicular á área de aplicação.
Resposta da questão 34: [C]
Página 42 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
A figura mostra as forças agindo sobre os êmbolos de áreas A1 e A2.
Aplicando o Teorema de Pascal:
F
P

A 2 A1

F
2

D
P
2
πD
4

F
4P
.
π
Resposta da questão 35: [D]
Dados: M  180g  18  10–2 kg; m  20g  2  10–2 kg; k  2  10–3 N / m; v  200m / s.
Pela conservação da quantidade de movimento calculamos a velocidade do sistema (vs)
depois da colisão:
Qdepois
 Qantes

sist
sist
M  m vs  m v
 200 v s  20  200  v s  20 m/s.
Depois da colisão, o sistema é conservativo. Pela conservação da energia mecânica
calculamos a máxima deformação (x) sofrida pela mola.
inicial
final
EMec
 EMec
x  20 

M  m  v 2s
18  2   102
2  10
3
2
 20 

k x2
2
20  102
2  10
3
 x  vs
 20  10 4
Mm
k

 x  20  10 2 m 
x  20 cm.
Resposta da questão 36: [B]
Página 43 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
Considerando o paciente e o bloco como pontos materiais, as forças atuantes em cada
um deles estão mostradas abaixo.
Como se trata de uma situação de equilíbrio, temos:
 T  m g I 


N  Ty  M g  N  T sen 30  M g


Fat  Tx  Fat  T cos30 III
II
(I) em (II):
N  m g sen 30  M g  N  50  10  m  10 
1
 N  500  5 m IV 
2
Na iminência de escorregar, a força de atrito estática no paciente atinge valor máximo.
Substituindo (IV) em (III):
μ N  m gcos30  0,26   500  5 m   m  10  0,87 
130  1,3  m  8,7  m  10  m  130 
m  13 kg
Resposta da questão 37: [A]
Dados: m = 0,4 kg; ΔS  1,6 m ; t = 0,8 s.
Calculando a aceleração escalar:
S 
2 S 2  1,6
a 2
3,2
t  a


 a  5 m /s2.
2
2
2
0,64
t
0,8
Página 44 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
A força de atrito sobre o copo é a resultante. Aplicando o Princípio Fundamental da
Dinâmica para o movimento retilíneo:
Fat  m a  Fat  0,4  5  Fat  2 N.
Resposta da questão 38: [A]
Como a catraca B gira juntamente com a roda R, ou seja, ambas completam uma volta
no mesmo intervalo de tempo, elas possuem a mesma velocidade angular: ωB  ωR .
Como a coroa A conecta-se à catraca B através de uma correia, os pontos de suas
periferias possuem a mesma velocidade escalar, ou seja: VA  VB .
Lembrando que V  ω.r : VA  VB  ωA .rA  ωB .rB .
Como: rA  rB  ωA  ωB .
Resposta da questão 39: [A]
A figura abaixo mostra as forças que agem no bloco.
As forças verticais anulam-se. Ou seja:
N  Fsen60  P  N  16x0,85  20  N  20  13,6  6,4N
Na horizontal FR  ma  Fcos60  ma  16x0,5  2a  a  4,0 m/s2
Página 45 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
Resposta da questão 40: [E]
A força F acelera o conjunto.
FR  ma  10  5a  a  2,0m / s2
A força de atrito acelera o bloco de baixo.
Fat  ma  Fat  4x2  8,0N
Resposta da questão 41: [B]
Como as velocidades escalares são iguais e constantes, de acordo com a figura e as
tabelas dadas, comparando as resultantes centrípetas temos:
Fc p 
M v2
R

M v2
1  M v2 
FK 

 FK  
2R
2  R 


 M v2 

3 M v2


F


F

3
 F
F
 R 
R




2
2
M v 
6Mv


 FS  2 
FS  3 R
 R 



 FK  FS  FF.
Resposta da questão 42: [A]
Dados: m = 50 kg; h = 5 m; v0 = 0; g = 10 m/s2.
1ª Solução: Pelo Teorema da Energia Cinética.
O sistema é não conservativo. O trabalho das forças não conservativas (W) corresponde,
em módulo, à energia mecânica dissipada, igual a 36% da energia mecânica inicial.
WFat  0,36 m g h
Pelo Teorema da Energia Cinética: o trabalho da força resultante é igual à variação da
energia cinética.
Página 46 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
W Re s  ΔECin
F
 WP  WFat 
m g h  0,36 m g h 
m v2
2
m v 2 m v 02

2
2

 v  0,64  2  g  h  1,28  10  5  64 
v  8 m / s.
2ª Solução: Pelo Teorema da Energia Mecânica.
Se houve dissipação de 36% da energia mecânica do sistema, então a energia mecânica
final (que é apenas cinética) é igual a 64% da energia mecânica inicial (que é apenas
potencial gravitacional).
final
inicial
EMec
 0,64 EMec

m v2
 0,64 m g h  v  1,28  g  h  1,28  10  5  64 
2
v  8 m / s.
Resposta da questão 43: [A]
Pelo teorema de Pascal aplicado em prensas hidráulicas, temos:
F1
F
 2
A1 A 2
O volume dos cilindros é dado por: V  A.h.
Nas condições apresentadas no enunciado, temos:
V2  4.V1
A 2 .h2  4.A1.h1
A 2 .h  4.A1.3h
A2  12.A1
Assim:
F1
F
F
 2  2  12
A1 12A1
F1
Página 47 de 48
MECÂNICA – SELEÇÃO – 3ª SÉRIE - 2016
Resposta da questão 44: [B]
Para forças de mesma intensidade (F), aplicadas perpendicularmente nas extremidades
das alavancas, para os três modelos, 1, 2 e 3, temos os respectivos momentos:
M1  F  40

M2  F  30
M  F  25
 3
 M1  M2  M3 .
Página 48 de 48