Aula 11 “Root Locus – LGR ” (Lugar Geométrico das Raízes) parte I

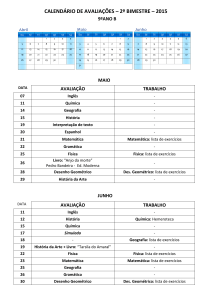
Aula 11
“Root Locus – LGR”
(Lugar Geométrico das Raízes)
parte I
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Sistema de malha fechada
G(s)
R(s)
+
-
K
G(s)
H(s)
G(s)
Y(s)
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Sistema de malha fechada
R(s)
+
-
K
G(s)
Y(s)
H(s)
O “Root Locus” é o lugar geométrico dos polos do
sistema de malha fechada, quando K varia.
Aqui vamos fazer sempre para K  0, mas também é possível
construir o “Root Locus” para K  0 ou para -  K  .
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
“Root Locus” (RL) = Lugar Geométrico das Raízes (LGR)
Mas o “Root Locus” é na verdade o lugar geométrico dos polos,
ou seja, das raízes da equação característica, do sistema de
malha fechada
R(s)
+
-
G(s)
Y(s)
Plano
Complexo
j eixo
H(s)
imaginário
0
eixo real
Logo, o “Root Locus” é traçado no plano complexo
É fácil de observar que o “Root Locus” é SIMÉTRICO em relação
ao eixo real
Ou seja, a parte de cima é um espelho da parte de baixo
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Como já sabemos, a “função de transferência” de malha
fechada (FTMF) do sistema é dada por
G(s)
F.T. 
1  G(s)H(s)
e os polos de malha fechada deste sistema são as raízes da
equação característica da FTMF
É fácil de mostrar que estas raízes da equação característica
da FTMF são as mesmas raízes que
1 + G(s)H(s) = 0
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Ou seja, calcula-se a expressão
1 + G(s)H(s) = 0
e depois calcula-se as raízes do numerador.
Estas serão raízes da equação característica da FTMF
sem a necessidade de calcular a FTMF
Na verdade, a equação característica desta FTMF é
justamente o numerador de
1 + G(s)H(s)
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 1:
R(s)
+
-
K  (2s  1)
(s  4)
Y(s)
1
s
Observe que:
K  (2s  1)
1  G(s)H(s)  1 
(s  4)s
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 1 (continuação)
logo,
s  (2K  4) s  K
1  G (s)H(s) 
(s  4) s
2
e portanto, a equação característica da FTMF é dada por:
s  (2K  4) s  K  0
2
que poderia igualmente ser obtida (embora com um pouco mais de
contas) através do denominador da FTMF, que é dada por:
K (2s  1) s
FTMF  2
s  (2K  4) s  K
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 2:
Vamos fazer o Root Locus do sistema M.F.
R(s)
+
-
K  (s  2)
(s  5)
Y(s)
Observe que:
K  (s  2)
1  G(s)H(s)  1 
(s  5)
(K  1) s  (5  2K)

(s  5)
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 2 (continuação)
R(s)
+
-
K  (s  2)
(s  5)
Logo, a equação característica do sistema M.F. é:
(K  1) s  (5  2K)  0
e o único polo de M.F. é:
(2K  5)
s 
(K  1)
Y(s)
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 2 (continuação)
R(s)
+
-
K  (s  2)
(s  5)
Y(s)
Portanto, o Root Locus deste sistema é o lugar geométrico de s
(2K  5)
s 
(K  1)
no plano complexo, quando varia-se o K, para K > 0.
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 2 (continuação)
Observe que:
s = –5
s → +2
se K = 0
se K → ∞
Portanto, é fácil de observar que o Root Locus deste sistema é
o segmento de reta no eixo real entre –5 e +2, isto é [–5 ,+2].
eixo
imaginário
x
–5
0
o
2
eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 2 (continuação)
Na verdade, o segmento de reta que vai de –5 para 2,
quando K vai de 0 a ∞.
e note que K = 2,5 quando s = 0.
K→0
K = 2,5
K→∞
eixo
imaginário
x
–5
0
o
2
eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 2 (continuação)
Como este sistema de M.F. é de 1ª ordem,
o único polo de M.F. é real,
e portanto,
este Root Locus fica inteiramente localizado no eixo real.
K→0
K = 2,5
K→∞
eixo
imaginário
x
–5
0
o
2
eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 2 (continuação)
O Root Locus permite-nos ver que
para K < 2,5  o sistema M.F. é estável,
pois neste caso o único polo M.F. estará no SPE, enquanto que
para K ≥ 2,5  o sistema M.F. não é estável.
K→0
K = 2,5
K→∞
eixo
imaginário
x
–5
0
o
2
eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 3:
R(s)
+
-
K
2
s  2s  3
Y(s)
Observe que:
K
1  G(s)H(s)  1 
(s  1) (s  3)

s  2s  (K  3)
s 2  2s  3
2
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 3 (continuação)
R(s)
+
-
K
s 2  2s  3
Logo, a equação característica do sistema M.F. é:
s2  2s  (K  3)  0
e os 2 polos de M.F. são:
s  1  4  K
Y(s)
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 3 (continuação)
R(s)
+
-
K
s 2  2s  3
Y(s)
Portanto, o Root Locus deste sistema é o lugar geométrico de s
s  1  4  K
no plano complexo, quando varia-se o K, para K > 0.
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 3 (continuação)
Observe que:
s = –3 e
se K = 0
s=1
eixo imaginário
K=0
K=0
x
–3
0
x
1
eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 3 (continuação)
além disso:
s  1  4  K polos reais
s   1 polos reais e duplos
se K < 4
se K = 4
eixo imaginário
K=4
K=0
x
–3
K=0
–1
0
x
1
eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 3 (continuação)
e ainda:
o Root Locus
passa pela origem
s  0
se K = 3
eixo imaginário
K=3
K=4
K=0
x
–3
–1
0
x
1
K=0
eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 3 (continuação)
Mas este Root Locus não fica restrito ao eixo real, pois
s  1  j K  4
se K > 4
K→∞
eixo imaginário
K=3
K=4
K=0
x
–3
–1
K→∞
0
x
1
complexos
conjugados
com parte real = –1
e a parte imaginária
variando de 0 a ∞.
K=0
eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 3 (continuação)
E mostrando os 2 ramos
deste Root Locus com
cores diferentes, como
faz o Matlab…
Resumindo, …
Este Root Locus tem 2 ramos
K→∞
eixo imaginário
K=3
K=4
K=0
x
–3
–1
K→∞
0
x
1
K=0
eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 3 (continuação)
E mostrando os 2 ramos
deste Root Locus com
cores diferentes, como
faz o Matlab…
K→∞
eixo imaginário
K=3
K=4
K=0
x
–3
–1
K→∞
0
x
1
K=0
eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 3 (continuação)
O Root Locus permite-nos ver que para K ≤ 3 
 o sistema M.F. não é estável,
enquanto que para K > 3  o sistema M.F. é estável,
pois neste caso os 2 polos M.F. estarão no SPE.
K→∞
eixo imaginário
K=3
K=4
K=0
x
–3
–1
K→∞
0
x
1
K=0
eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Note que o “Root Locus” depende apenas do produto
G(s)H(s) e não de G(s) ou de H(s) separadamente.
Portanto, se os 2 sistemas de malha fechada abaixo
R(s)
+
-
G1(s)
Y(s)
R(s)
+
-
H1(s)
G2(s)
Y(s)
H2(s)
satisfazem
G1(s)H1(s) = G2(s)H2(s)
então os “Root Locus” destes dois sistemas serão o mesmo
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
A expressão
G(s)H(s)
é chamada de função de transferência do sistema
em malha aberta (FTMA).
G(s)H(s)
(FTMA)
R(s)
é como
malha fosse
aberta aqui
tornando-se
aberta
+
-
G(s)
H(s)
Y(s)
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Portanto, os polos e zeros de
G(s)H(s)
são chamados de polos e zeros de malha aberta.
Vamos chamar de n e m o número de polos e zeros de
G(s)H(s), respectivamente
ou seja:
n = número de polos de malha aberta
m = número de zeros de malha aberta
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regras para a construção do
“Root Locus”
A seguir vamos apresentar 8 regras que auxiliarão na elaboração
do esboço do “Root Locus” para um sistema de malha fechada
com FTMA dada por G(s)H(s).
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #1
Número de ramos
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #1 – Número de ramos
O número de ramos n de um “Root Locus” é o número
de polos de malha aberta, ou seja, o número de polos
de G(s)H(s).
n = nº ramos = nº polos de G(s)H(s)
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #2
Intervalos com e sem “Root Locus” no eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #2 – Intervalos com e sem “Root Locus” no eixo real
Um ponto s no eixo real pertencerá ao “Root Locus” se
houver um número ímpar de polos e zeros reais de malha
aberta a direita de s.
ou seja, se houver um número ímpar de polos e zeros reais
de G(s)H(s) a direita de s.
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 4:
x
x
x
Aplicação da Regra #2 –
Intervalos com e sem “Root Locus” no eixo real
o
x
x
o
x
0
0
o
o
x o
x
o
eixo real
o
x
x
eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 4 (continuação)
Aplicação da Regra #2
x
x
o
x
o
0
x
oo
eixo real
x
x
xx
o
o
o
o
0
x
x
o
x
eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 5:
Aplicação da Regra #2 –
Intervalos com e sem “Root Locus” no eixo real
Considere o sistema de M.F. no qual
K
G(s)H(s) 
(s  1) (s  2) (s  3)
x
–3
x
–2
x
–1
0
eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #3
Pontos de início e término dos ramos do “Root Locus”
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #3 – Pontos de início e término dos ramos do “Root Locus”
Os n ramos do “Root Locus” começam nos n polos de
malha aberta
ou seja, começam nos n polos de G(s)H(s)
m dos n ramos do “Root Locus” terminam nos m zeros de
malha aberta
ou seja, terminam nos m zeros de G(s)H(s)
e os restantes:
(n – m) ramos do “Root Locus” terminam no infinito ()
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #3 – Pontos de início e término dos ramos do “Root Locus”
(continuação)
Note que (n – m) é a diferença entre o número de polos de
malha aberta n e o número de zeros de malha aberta m
i.e., a diferença entre o número de polos e zeros de
G(s)H(s)
Se n = m então (n – m) = 0, e portanto nenhum ramo
termina no infinito ()
Logo, se o número de polos de malha aberta for igual ao
número de zeros de malha aberta, então nenhum ramo
termina no infinito ()
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #4
Assíntotas no infinito
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #4 – Assíntotas no infinito
Para os (n – m) ramos do “Root Locus” que não terminam
nos m zeros de malha aberta, isto é, os m zeros finitos de
G(s)H(s), pode-se determinar a direção que eles vão para
o infinito no plano complexo.
 = ângulo da assíntota com o eixo real
180º(2i  1)

(n  m)
i  0,1, 2,
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #4 – Assíntotas no infinito
(continuação)
Aplicando-se a fórmula obtém-se a tabela abaixo:
n–m
1
2
3
4
5
6


 = ângulo da assíntota com o eixo real
180º
90º e –90º
60º, –60º e 180º
45º, –45º, 135º e –135º
36º, –36º, 108º, –108º e 180º
30º, –30º, 90º, –90º, 150º e –150º




Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #5
Pontos de interseção das assíntotas com o eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #5 – Pontos de interseção das assíntotas com o eixo real
As (n – m) assíntotas no infinito ficam determinadas
pelas suas direções (ângulos ) e pelo ponto onde eles
se encontram no eixo real, o dado pela expressão:
m
 n

  Re( pi )   Re( z j ) 


i

1
j

1

o  
( n  m)
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #6
Pontos do eixo real onde há encontro de ramos
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #6 – Pontos do eixo real onde há encontro de ramos
Primeiro constrói-se a equação
1 + G(s)H(s) = 0,
e daí obtém-se uma expressão para K em função de s:
K(s)
então calcula-se a derivada de K em relação a s, dK/ds
Agora, através da equação abaixo em s
dK
0
ds
obtém-se os pontos s do eixo real onde há encontro de ramos
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #6 – Pontos do eixo real onde há encontro de ramos
(continuação)
A equação em s
dK
0
ds
em geral tem um número de soluções
s = s1
s = s2
s = s3
s = s4
s = s5 … … …
maior que o número de pontos de
encontro de ramos no eixo real
É necessário cancelar as soluções que não sejam pontos
pertencentes ao “Root Locus”
s = s1
s = s2
s = s3
s = s4
s = s5 … … …
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #6 – Pontos do eixo real onde há encontro de ramos
(continuação)
eixo real
Quando há encontro de ramos no eixo real pode ser ramos
que se encontram e ENTRAM no eixo real ou ramos que se
encontram e PARTEM do eixo real.
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #6 – Pontos do eixo real onde há encontro de ramos
(continuação)
Para um ponto
s = s’
onde há encontro de ramos no eixo real,
calculamos a segunda derivada de K(s) em s = s’
d 2K
ds 2 ss'
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #6 – Pontos do eixo real onde há encontro de ramos
(continuação)
Se
d 2K
 0
2
ds ss'
s’
eixo real
 2 ramos que se encontram e PARTEM do eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #6 – Pontos do eixo real onde há encontro de ramos
(continuação)
Se
d 2K
 0
2
ds ss'
s’
eixo real
 2 ramos que se encontram e ENTRAM no eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #6 – Pontos do eixo real onde há encontro de ramos
(continuação)
Se
d 2K
 0
2
ds ss'
s’
eixo real
 mais de 2 ramos que se encontram neste ponto
 prosseguir para Regra #7 – Encontro de mais de dois ramos
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 6:
Aplicação da Regra #6 –
Pontos do eixo real onde há encontro de ramos
Retornando ao Exemplo 1, fazendo
K  (2s  1)
1  G(s)H(s)  1 
 0
(s  4) s
tem-se que:
(s  4) s
K  
(2s  1)
e portanto:
dK
2 (s 2  s  2)

 0
2
ds
(2s  1)
Logo, s = 1 e s = –2 são os pontos onde há
encontro de ramos
s=1
s = –2
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 6 (continuação)
Aplicação da Regra #6
Para se saber o valor de K em cada um destes pontos
é necessário substituí-los (s = 1 e s = –2) na expressão
de K
Logo, os pontos onde há
encontro de ramos são
(s  4)s
K  
 1
(2s  1) s1
(s  4)s
K  
 4
(2s  1) s2
s = 1 (K = 1)
s = –2 (K = 4)
e
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 6 (continuação)
Aplicação da Regra #6
os pontos onde há encontro de ramos são
s = 1 (K = 1)
e
s = –2 (K = 4)
K=4
K=1
s’’= –2
0
s’= 1
eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 6 (continuação)
Aplicação da Regra #6
Agora para se saber se cada um destes encontro de ramos
são de ramos que CHEGAM ou de ramos que PARTEM, é
necessário calcular a segunda derivada
d 2K
18
 
2
ds
(2s  1)3
substituindo-se pelos pontos onde há encontro de ramos:
s=1
e
s = –2
d 2K
 18
2



 0
2
3
ds s 1
(2s  1) s 1
3
d 2K
ds 2
s  2
 18

(2s  1)3
s  2
2
 
 0
3
ramos que PARTEM
do eixo real
ramos que ENTRAM
no eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 6 (continuação)
Aplicação da Regra #6
Logo, os pontos onde há encontro de ramos são:
s = 1 (K = 1) ramos que PARTEM do eixo real
s = –2 (K = 4) ramos que ENTRAM no eixo real
K=4
s’’= –2
K=1
0
s’= 1
eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 7:
Aplicação da Regra #6 –
Pontos do eixo real onde há encontro de ramos
Retornando ao Exemplo 5
K
G(s)H(s) 
(s  1) (s  2) (s  3)
então
K
1  G(s)H(s)  1 
 0
(s  1) (s  2) (s  3)
K   (s  1) (s  2) (s  3)
  s 3  6 s 2  11s  6
dK
  3 s 2  12 s  11
ds
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 7 (continuação)
Aplicação da Regra #6
logo, fazendo
dK
 0
ds
 3s2 12 s 11  0
s = – 2,58
concluímos que
somente uma das
soluções,
s = –1,423
s = –1,423
está num
intervalo com
“Root Locus”
agora, observando os intervalos com e sem
“Root Locus” no eixo real (exemplo 5)
x
–3
x
–2
x
–1
0
eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #7
Encontro de mais de dois ramos
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #7 – Encontro de mais de dois ramos
Na aplicação da regra anterior se
d2K
0
2
ds ss'
isto significa que há encontro de mais de dois ramos e tem que
se continuar a derivar K(s) para derivadas de ordem mais altas
dkK
ds k
k  3, 4, 5,
até que
d ηK
0
η
ds ss'
para algum η
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #7 – Encontro de mais de dois ramos (continuação)
Se
d K
0

ds ss'
e
dk K
0
k
ds ss'
para  k < η
isto significa que há encontro de η ramos em s’
ou seja, η ramos
CHEGAM
e η ramos
PARTEM
em s’
O encontro de 3 ramos ou mais não é muito comum
Certamente ocorre com menos frequência que o encontro
de 2 ramos (Regra #6)
Portanto esta Regra #7 não é sempre utilizada. Somente
naqueles casos em que, ao aplicar a Regra #6, nós
encontrarmos
d2K
0
2
ds ss'
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #7 – Encontro de mais de dois ramos (continuação)
Um encontro de 3 ramos em s’ pode ter o seguinte aspeto
3 ramos CHEGAM
e 3 ramos PARTEM
em s’
s’
eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Regra #7 – Encontro de mais de dois ramos (continuação)
Um encontro de 4 ramos em s’ pode ter o seguinte aspeto
4 ramos CHEGAM
e 4 ramos PARTEM
em s’
s’
eixo real
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 8:
Aplicação da Regra #7 –
Encontro de mais de dois ramos
K
G(s)H(s)  3
(s  1)
1  G(s)H(s)  0
dK
  3s2  0
ds
d2K
  6s s0  0
2
ds s0
K   s 1
3
s’ = 0
aplicar Regra #7
(a começar pela
derivada de 3ª ordem)
Root Locus – LGR (Lugar Geométrico das Raízes) parte I
______________________________________________________________________________________________________________________________________________________________________________________
Exemplo 8 (continuação)
d 3K
 6  0
3
ds s0
Aplicação da Regra #7
encontro de 3 ramos em
s’ = 0
K=∞
3 ramos CHEGAM
e 3 ramos PARTEM
em s’= 0
K=∞
Este exemplo apenas ilustra
a aplicação da Regra #7
Para fazer o esboço deste
“Root Locus” completo é
necessário aplicar todas as
regras
–0,5 + 0,866j
K = 0x
K=1
s’= 0
K=0
x
1
eixo real
K=0 x
–0,5 – 0,866j
K=∞
Obrigado!
Felippe de Souza
[email protected]