1 a √

1.
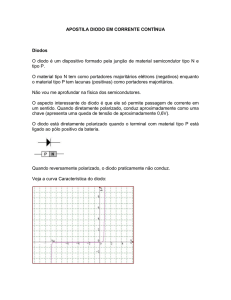
Seja o retificador mostrado abaixo, onde V1(ωt)=220sen(wt); R= 20Ω e L=100mH; f=50Hz.
Calcular VLmed, ILmed.e o FP da estrutura.
D1
R
V1(ωt)
L
Solução:
Cálculo do ângulo de extinção de corrente β:
a
α=0
√2 (1.1)
0
314,16 0,1
cos 0,537
20
Através do ábaco de Puschlowski obtêm-se com:
cos α=0
a= 0
cosΦ=0,4
β=254°
cosΦ=0,6
β=236°
Fazendo uma média obtêm-se
α=0
a= 0
cosΦ=0,55
(1.2)
(1.3)
(1.4)
β=240,5°
2#
% '
$
Onde m é o número de pulsos do conversor e α é o ângulo de início de condução do diodo.
Cálculo do ângulo crítico de extinção de corrente βc:
!" (1.5)
Para este circuito tem-se α=0 e m=1.
Βc=360°
(1.6)
,
- √2 . /,012
2#
(1.7)
Como β< βc , é condução descontínua.
Cálculo da tensão média na carga VLmed:
()*+
3
45
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução e β é o ângulo de fim de
condução do diodo.
()*+
678,9°
1
- 220 /,012 52,52
2#
8
()*+ ; 52,52
2,63<
20
(1.8)
Cálculo da corrente média na carga ILmed:
Cálculo do fator de potência:
:()*+ (1.9)
Para o cálculo do fator de potência é necessário o valor da corrente eficaz na carga e na fonte de tensão,
que neste caso é o mesmo para os dois.
1
314,16 0,1
(1.10)
57,52°
20
Utilizando o ábaco da Fig.2.8 do livro de Eletrônica de Potência 6ª edição de Ivo Barbi para correntes
normalizadas obtêm-se:
Sendo
(1.11)
Ief=0,63A
Portanto:
> ?6 % 0 16 37,23@
:(*A Potência dissipada na carga:
√2 8 :*A 220 0,63
3,72<
>
37,23
(1.12)
(1.13)
P=R·ILef2
(1.14)
P=20·3,72²=276,77 W
(1.15)
S=Vef·Ief
(1.16)
Potência aparente na fonte:
C 276,77
0,478
D 578,68
(1.17)
S=155,56·3,72=578,68 VA
BC (1.18)
2.
Considere o conversor abaixo onde V(ωt)=220sen(ωt)
E=120V; L=100mH; R=8Ω; f= 50Hz
D
1
R
L
V(ωt)
E
a)
Calcule o ângulo de extinção da corrente e defina o modo de condução.
b)
Apresente as formas de onda e calcule VLmed e ILmed..
c)
Sendo E=0V e R= 20Ω, adicione em anti-paralelo com a carga um diodo e calcule o valor da
indutância para se obter condução crítica.
Solução:
a)
Cálculo do ângulo de extinção de corrente β:
Devido a presença de fonte E na carga o ângulo de início de condução do diodo deixa de ser α=0° e
passa a ser o ângulo θ1 em que a fonte de entrada tem seu valor igual ao da fonte E, onde a partir desse
momento polarizando positivamente o diodo dando início a condução.
Para determinar o ângulo θ1 deve se igualar a tensão E com a tensão de entrada e isolar ωt, pois neste
instante ωt= θ1.
220·sen(ωt)=120
α= Θ1 = ωt = 33,05°=0,576 rad
(2.1)
2
a
cos √ 2 120
220
0,55
314,16 0,1
cos 0,247
8
(2.2)
(2.3)
Através do ábaco de Puschlowski e fazendo médias sucessivas obtêm-se:
α=33,05°
a= 0,4
α=33,05°
a= 0,6
cos ϕ = 0, 2
cos ϕ = 0, 4
cos ϕ = 0,3
β
β
β
cos ϕ = 0, 25 β
= 221°
= 210°
= 215, 5°
cos ϕ = 0, 2
cos ϕ = 0, 4
cos ϕ = 0,3
= 194°
= 187°
= 190, 5°
β
β
β
cos ϕ = 0, 25 β
= 218, 25°
(2.4)
= 192, 25°
Fazendo uma média obtêm-se
a= 0,5
cos ϕ = 0, 25
a= 0,55 cos ϕ = 0, 25
β = 205, 25°
β = 198, 75° = 3, 47rad
2#
% '
$
Onde m é o número de pulsos do conversor e α é o ângulo de início de condução do diodo.
Cálculo do ângulo crítico de extinção de corrente βc:
!" (2.5)
Para este circuito monofásico de meia onda tem-se m=1 e α= 33,05° logo,
βc=360+33,05=393,05°
(2.6)
Como β< βc tem-se condução descontínua.
b)
Formas de onda
V(ωt)
400V
200V
0
V
-200V
-400V
400V
VL
200V
0
V
-200V
-400V
400V
VD1
200V
0
V
-200V
-400V
4.0A
IL
2.0A
0A
0
π
2π
3π
4π
3
Cálculo da tensão média na carga VLmed:
()*+
46
4H
,
G - √2 . /,012 % - 2 I
2#
45
(2.7)
46
Onde n é o número de pulsos do conversor,θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo (extinção da corrente β) e θ3 é o ângulo de reinício de condução do diodo.
()*+
5NO,L9°
1
G 2#
HH°
220 /,012 %
6JK8,9LM
-
H,7L
1202 I 127,25
()*+ ; 127,25 ; 120
0,906<
8
(2.8)
Cálculo da corrente média na carga ILmed:
:()*+ c)
(2.9)
Indutância necessária para condução critica Lc:
Colocando um diodo em anti-paralelo, torna-se o circuito em um circuito monofásico de meia onda com
roda livre, onde para que haja condução critica é necessário que
#
5Q (2.10)
Onde π é o ângulo em que se tem roda livre, ou seja, é o tempo em que o indutor se descarregará
através do resistor até a fonte de entrada voltar a carregar o indutor. ω é a freqüência angular e τ é a constante
de tempo do circuito dada por L/R.
Portanto para que haja condução contínua é necessário que o tempo de 5τ seja maior que o tempo em
que a fonte fica sem fornecer energia à carga. Logo.
#. #. 20
40$S
5
5.314,16
(2.11)
3.
Para o retificador monofásico de onda completa com ponto médio abaixo.
R=2Ω; L=3mH; E=36V; V(ωt)=180sen(ωt); f=50Hz; rt=10mΩ; Vto=1V; Ta= 50°C; N1/N2=3
D
1
R
N
2
V(ωt)
L
N
1
N
2
E
D
2
a)
b)
c)
Calcular o ângulo de extinção da corrente, βc e definir o modo de condução.
Traçar as formas de onda.
Calcular VLmed, ILmed.e, se possível ILef.
Solução:
Sendo N1/N2=3 a tensão nas bobinas do transformador no secundário é V2(ωt)=60sen(ωt).
a)
Cálculo do ângulo de extinção de corrente β:
Devido a presença de fonte E na carga o ângulo de início de condução do diodo deixa de ser α=0° e
passa a ser o ângulo θ1 em que a fonte de entrada tem seu valor igual ao da fonte E, onde a partir desse
momento polarizando positivamente o diodo dando início a condução.
4
Para determinar o ângulo θ1 deve se igualar a tensão E com a tensão de entrada e isolar ωt, pois neste
instante ωt= θ1.
60·sen(ωt)=36
α =Θ1 = ωt = 36,87°=0,644 rad
a
√ 2 36
60
(3.1)
0,6
(3.2)
314,16 3$
cos 0,9
2
Através do ábaco de Puschlowski obtêm-se:
cos a=0,6
cosΦ=0,9
(3.3)
(3.4)
β=164° ou 2,862 rad
2#
% '
$
Onde m é o número de pulsos do conversor e α é o ângulo de início de condução do diodo.
Cálculo do ângulo crítico de extinção de corrente βc:
!" (3.5)
Para circuito monofásico de ponto médio, m=2 e α=36,87°.
Logo,
βc=180+36,87°=216,87°
(3.6)
Como β< βc tem-se condução descontínua.
b)
Formas de onda
100V
V(ωt)
0V
-100V
100V
VL
50V
0V
0V
VD1
-100V
-200V
10.0A
IL
5.0A
0A
π
0
c)
Cálculo da tensão média na carga VLmed:
()*+
46
3π
2π
4H
,
G - √2 . /,012 % - 2 I
2#
45
46
4π
(3.7)
5
Onde n é o número de pulsos do conversor,θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo (extinção da corrente β) e θ3 o ângulo de reinício de condução do diodo.
()*+
5M7,88°
2
G 2#
HM,OL°
60 /,012 %
JK8,M77
-
6,OM6
362 I 44,22
(3.8)
()*+ ; 44,22 ; 36
4,11<
2
Cálculo da corrente média na carga ILmed:
:()*+ (3.9)
Cálculo da corrente eficaz na carga ILef:
Como a condução é descontínua, as harmônicas de ordem superior não podem ser desprezadas e o
cálculo se torna muito complexo.
4.
Considere o circuito abaixo.
V(ωt)=√2 220sen(ωt); f= 60Hz; R=20Ω; E=60V.
D1
D2
R
V(ωt)
D5
D3
E
D4
a)
Traçar as formas de onda V(ωt), VL(ωt), IL(ωt) e VD1.
b)
Calcule o valor da tensão média, corrente média e da corrente eficaz na carga.
c)
Calcular o valor da resistência térmica entre junção e o ambiente para que o diodo D5 se
mantenha com uma temperatura de junção de 150°C
Solução:
Analisando o circuito, vê-se que o diodo D5 nunca entrará em condução, pois como não se tem
indutância no circuito, a menor tensão que aparecerá na carga será a da própria fonte E, polarizando
negativamente o diodo D5.
a)
Formas de onda:
Ângulo de inicio de condução θ1
Para determinar o ângulo θ1 deve se igualar a tensão E com a tensão de entrada e isolar ωt, pois neste
instante ωt= θ1.
311·sen(ωt)=60
Θ1 = ωt = 11,12°=0,194 rad
(4.1)
6
400V
V(ωt)
0V
-400V
400V
VL
200V
0V
0V
VD1
-200V
-400V
20A
IL
10A
0A
b)
3π
2π
π
0
Cálculo da tensão média na carga VLmed:
()*+
46
4H
,
G - √2 . /,012 % - 2 I
2#
45
46
4π
(4.2)
Onde n é o número de pulsos do conversor,θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo (extinção da corrente β) e θ3 o ângulo de reinício de condução do diodo.
()*+
311·sen(ωt)=60
Θ1 = ωt = 11,12°=0,194 rad
(4.3)
Θ2=ωt=180-11,12=168,88°=2,948 rad
(4.4)
Θ3=π + 0,194 rad
(4.5)
5MO,OO°
2
G 2#
55,56°
311 /,012 %
JK8,5N7
-
6,N7O
602 I 201,68
()*+ ; 201,68 ; 60
7,084<
20
(4.6)
Cálculo da corrente média na carga ILmed:
:()*+ (4.7)
7
Cálculo da corrente eficaz na carga ILef:
:(*A
T
c)
ambiente.
5.
46
,
√2 . /,01 ; T
-U
V 2 2#
5MO,OO°
2
2#
55,56°
6
45
0
(4.8)
311 /,01 ; 60 6
1 2 8,37<
20
Como o diodo não entra em condução, a temperatura do diodo se mantém em temperatura
Considere o conversor abaixo com:
V(ωt)=√2 220sen(ωt); f= 60Hz; R=1Ω; L=1000mH; E=60V.
D1
D2
R
V(ωt)
L
D3
E
D4
a)
b)
c)
Calcular o ângulo de extinção da corrente, βc e definir o modo de condução.
Traçar as formas de onda V(ωt), VL(ωt), IL(ωt) e VD1.
Calcule o valor da tensão média, corrente média e da corrente eficaz na carga.
Solução:
a)
Cálculo do ângulo de extinção de corrente β:
Devido a presença de fonte E na carga o ângulo de início de condução do diodo deixa de ser α=0° e
passa a ser o ângulo θ1 em que a fonte de entrada tem seu valor igual ao da fonte E, onde a partir desse
momento polarizando positivamente o diodo dando início a condução.
Para determinar o ângulo θ1 deve se igualar a tensão E com a tensão de entrada e isolar ωt, pois neste
instante ωt= θ1.
a
311·sen(ωt)=60
(5.1)
60
(5.2)
α =Θ1 = ωt = 11,12°=0,194 rad
√ 2 √2. 220
0,193 W 0,2
377 1
cos 2,65$ W 0
1
Através do ábaco de Puschlowski se obtêm:
cos α=11,12°
a=0,2
cosΦ=0
β=274° ou 2,862 rad
2#
% '
$
Onde m é o número de pulsos do conversor e α é o ângulo de início de condução do diodo.
(5.3)
(5.4)
(5.5)
Cálculo do ângulo crítico de extinção de corrente βc:
!" (5.6)
8
Para este circuito monofásico de onda completa tem-se m=2 e α=11,12°.
βc=180+11,12°=191,12°
(5.7)
Como β> βc tem-se condução contínua.
b)
Formas de onda
400V
V(ωt)
0V
-400V
400V
VL
0V
-400V
400V
VD1
0V
-400V
IL
150A
100A
50A
0A
π
0
c)
2π
3π
4π
Cálculo da tensão média na carga VLmed:
()*+
46
,
- √2 . /,012
2#
45
(5.8)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo e θ2 é o ângulo
de fim de condução do diodo.
()*+
5O8,88°
2
2#
8°
311 /,012 198,0
(5.9)
Cálculo da corrente média na carga ILmed:
:()*+ ()*+ ; 198,0 ; 60
138,0<
1
(5.10)
9
Cálculo da corrente eficaz na carga ILef:
Como a condução é contínua, e β é maior que βc o suficiente para considerar a corrente na carga uma
constante. Então:
:(*A :()*+ 138,0<
6.
(5.11)
Considere o retificador trifásico com ponto médio da figura abaixo.
V1(ωt)=√2 220sen(ωt); V2(ωt)=√2 220sen(ωt+120°); V3(ωt)=√2 220sen(ωt-120°); f= 60Hz; R=5Ω;
L=3000mH; rt=11mΩ; Vto=1V; Ta=40°C.
V1(ωt)
D1
V2(ωt)
D2
R
V3(ωt)
D3
L
a)
Traçar as formas de onda V1, V2, V3, VL, IL e VD2.
b)
Calcular VLmed, ILmed, ILef, VD1, IDmed, IDef.
c)
Calcular o valor da resistência térmica entre junção e o ambiente para que o diodo D2 se
mantenha com uma temperatura de junção inferior à 150°C.
d)
Calcular o FP da fonte 2.
Solução:
a)
Formas de onda:
Cálculo do ângulo de extinção de corrente β:
a
α=30°.
√ 2 (6.1)
0
377 3
cos 0
5
Através do ábaco de Puschlowski obtêm-se:
cos α=30°
a= 0
cosΦ=0
β= 330°
2#
% '
$
Para este circuito trifásico de ponto médio tem-se m=3 e α= 30° logo,
(6.2)
(6.3)
(6.4)
Cálculo do ângulo crítico de extinção de corrente βc:
!" βc=120+30=150°
(6.5)
(6.6)
Como β> βc tem-se condução contínua.
10
400V
V1(ωt)
V2(ωt)
V3(ωt)
200V
0V
-200V
-400V
400V
VL
200V
0V
0V
VD2
-250V
-500V
100A
IL
50A
0A
b)
2π
π
0
3π
4π
Cálculo da tensão média na carga VLmed:
()*+
46
,
- √2 . /,012
2#
45
(6.7)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo.
()*+
598°
3
- 311 /,012 257,19
2#
H8°
()*+ ; 257,19
51,44<
5
(6.8)
Cálculo da corrente média na carga ILmed:
:()*+ (6.9)
Cálculo da corrente eficaz na carga ILef:
Como a condução é contínua, e β é maior que βc o suficiente para considerar a corrente na carga uma
constante. Então:
:(*A :()*+ 51,44<
(6.10)
11
Cálculo da tensão de pico de D1 VD1:
XY √2 √3 8 √2 √3 220 538,88
(6.11)
Cálculo da corrente média no diodo:
:()*+ 51,44
17,15<
3
3
No circuito trifásico o diodo conduz em 1/3 do tempo total do ciclo. Então:
:X)*+ (6.12)
Cálculo da corrente eficaz no diodo:
:X*A c)
6J
H
:(*A 51,44
T 1
- 0:(*A 16 2 29,70<
2#
√3
√3
(6.13)
8
Resistência junção-ambiente:
Cálculo da potência dissipada em um diodo:
C Z :X*A 6 % [. :X)*+ 11$ 29,706 % 1 17,15 26,85\
(6.14)
]^ ; ]_ ^_ C
(6.15)
Cálculo da resistência junção-ambiente.
^_ d)
]^ ; ]_ 150 ; 40
4,10°`/\
C
26,85
Fator de potência:
BC C
D
C( :(*A 6 5 51,446 13230,37\
(6.16)
(6.17)
Cálculo da potência ativa na carga:
(6.18)
A potência ativa na fonte pode ser dada pela potência ativa na carga pela quantidade de fontes
presentes no circuito.
C( 13230,37
4410,12\
3
3
Cálculo da potência aparente da fonte:
Cb (6.19)
A potência aparente na fonte é dada pela tensão eficaz da fonte e pela corrente eficaz na fonte, que
neste caso é dado pela corrente eficaz no diodo.
D *A . :*A 220 29,70 7407,40<
Cálculo do fator de potência:
BC 4410,12
0,595
7407,40
(6.20)
(6.21)
12
7.
Para o retificador trifásico com ponto médio da figura abaixo.
V1(ωt)=√2 220sen(ωt); V2(ωt)=√2 220sen(ωt-120°); V3(ωt)=√2 220sen(ωt+120°); f= 60Hz; R=2Ω;
L=26mH; E=124V.
V1(ωt)
D1
V2(ωt)
D2
R
V3(ωt)
D3
L
E
a)
b)
c)
Obtenha o ângulo de extinção da corrente, o ângulo crítico e determine o modo de condução.
Traçar as formas de onda VL(ωt), IL(ωt) e VD1.
Calcular VLmed, ILmed, ILef, VDp, IDmed, IDef.
Solução:
a)
Cálculo do ângulo de extinção de corrente β:
Devido a presença da fonte é necessário verificar se o ângulo em que a fonte de entrada torna-se maior
do que o do valor da fonte E é maior ou menor do que 30° a fim de verificar a influência da fonte E no início de
condução do diodo.
311·sen(ωt)=124
(7.1)
Θ1 = ωt = 23,50°
Como o ângulo em que a fonte de entrada ultrapassa o valor da fonte E é menor do que 30°(ângulo em
que uma fonte de entrada se torna a fonte com o maior valor de tensão do circuito forçando a condução do
diodo) se tem
α=30°.
a
√ 2 cos 124
√2 220
(7.2)
0,40
377 26$
cos 0,2
5
(7.3)
(7.4)
Através do ábaco de Puschlowski e fazendo médias sucessivas obtêm-se:
α=30° a= 0,4
cosΦ=0,2
β= 221°
2#
% '
$
Para este circuito trifásico de ponto médio, m=3 e α= 30° logo,
(7.5)
Cálculo do ângulo crítico de extinção de corrente βc:
!" βc=120+30=150°
(7.6)
(7.7)
13
Como β>βc tem-se condução contínua.
b)
Formas de onda
400V
V1(ωt)
V2(ωt)
V3(ωt)
0V
-400V
400V
VL
200V
0V
VD1
0V
-250V
-500V
100A
IL
75A
50A
25A
0A
c)
2π
π
0
3π
4π
Cálculo da tensão média na carga VLmed:
()*+
46
,
- √2 . /,012
2#
45
(7.8)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo.
()*+
598°
3
- 311 /,012 257,19
2#
H8°
()*+ ; 257,19 ; 124
66,6<
2
Cálculo da corrente eficaz na carga ILef:
(7.9)
Cálculo da corrente média na carga ILmed:
:()*+ (7.10)
Como a condução é contínua, e β é maior que βc o suficiente para considerar a corrente na carga uma
constante. Então :
:(*A :()*+ 66,6<
(7.11)
Cálculo da tensão de pico de D1 VD1:
14
XY √2 √3 8 √2 √3 220 538,88
(7.12)
Cálculo da corrente média no diodo:
:()*+ 66,6
22,2<
3
3
No circuito trifásico o diodo conduz em 1/3 do tempo total do ciclo. Então:
:X)*+ Cálculo da corrente eficaz no diodo:
:X*A 6J
H
(7.13)
:(*A 66,66
T1
- 0:(*A 16 2 38,45<
2#
√3
√3
(7.14)
8
8.
Considere o conversor abaixo com tensão eficaz de linha de 440V, f=60Hz, Vto=0,5V e rt=8mΩ.
R=2Ω; L=100mH; E=350V;
D
1
V1(ωt
)
D
2
D
3
V2(ωt
)
R
L
V3(ωt
)
E
D
4
a)
b)
c)
d)
D
5
D
6
Calcular o ângulo de extinção da corrente, o ângulo crítico e determinar o modo de condução.
Traçar as formas de onda V1, V2, V3, VL, IL, ID1, VD1 e calcular VLmed, ILmed, IDmed, IDef
Calcular a potência dissipada e a tensão máxima em cada diodo.
Calcular o rendimento da estrutura e o FP.
Solução:
a)
Cálculo do ângulo de extinção de corrente β:
É necessário verificar se o ângulo em que a fonte de entrada torna-se maior do que o do valor da fonte E
é maior ou menor do que 60° a fim de verificar a influência da fonte E no início de condução do diodo.
622,25·sen(ωt)=350
Θ1 = ωt = 34,23°
(8.1)
Como o ângulo em que a fonte de entrada ultrapassa o valor da fonte E é menor do que 60°(ângulo em
que uma tensão de linha se torna a maior no circuito forçando a condução dos diodos) se tem:
a
√ 2 √ 3 cos 350
α=60°.
√2 440
0,57 W 0,6
377 100$
cos W 0
2
(8.2)
(8.3)
(8.4)
Através do ábaco de Puschlowski e fazendo médias sucessivas obtêm-se:
15
α=60°
a= 0,6
cosΦ=0
β= 199°
(8.5)
2#
% '
$
Para este circuito em ponte de Graetz, m=6 e α= 60° logo,
Cálculo do ângulo crítico de extinção de corrente βc:
!" (8.6)
βc=60+60=120°
(8.7)
Como β>βc tem-se condução contínua.
b)
Formas de onda
400V
V1(ωt)
V2(ωt)
V3(ωt)
0V
-400V
VL
500V
250V
0V
0V
VD1
-250V
-500V
200A
IL
ID1
100A
-10A
c)
2π
π
0
3π
4π
Cálculo da tensão média na carga VLmed:
()*+
46
,
- √2 √3 . /,012
2#
45
(8.8)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução de um par de diodos, θ2
é o ângulo de fim de condução do par de diodos.
()*+
568°
6
- 622,25 /,012 594,2
2#
M8°
(8.9)
Cálculo da corrente média na carga ILmed:
16
:()*+ ()*+ ; 594,2 ; 350
122,1<
2
(8.10)
Cálculo da corrente eficaz na carga ILef:
Como a condução é contínua, e β é maior que βc o suficiente para considerar a corrente na carga uma
constante. Então:
:(*A :()*+ 122,1<
(8.11)
XY √2 √3 8 √2 440 622,25
(8.12)
Cálculo da tensão de pico de D1 VD1:
Cálculo da corrente média no diodo:
:()*+ 122,1
40,7<
3
3
No circuito em ponte de Graetz cada diodo conduz em 1/3 do tempo total do ciclo. Então:
:X)*+ (8.13)
Cálculo da corrente eficaz no diodo:
:X*A d)
6J
H
:(*A 122,1
T 1
- 0:(*A 16 2 70,49<
2#
√3
√3
(8.14)
8
Cálculo do rendimento:
Para o cálculo do rendimento verifica-se potência entregue na carga pela potência entregue pelas
fontes(potência dissipada nos diodos e potência dissipada na carga)
c
c
:()*+ % :(*A 6
:()*+ % :(*A 6 % 60Z :X*A 6 % [. :X)*+ 1
350 122,1 % 2 122,1
0,995
350 122,1 % 2 122,16 % 608$ 70,496 % 5 40,71
6
Cálculo do fator de potência:
BC C
D
(8.15)
(8.16)
C :()*+ % :(*A 6 350 122,1 % 2 122,16 72551,82\
(8.17)
D 3 d :*Ae 3 254,03 99,69 75972,75<
(8.18)
Cálculo da potência dissipada na carga:
Cálculo da potência aparente entregue pelas fontes
BC C 72551,82
0,955
D 75972,75
(8.19)
17
9.
Deseja-se utilizar o retificador com filtro capacitivo para alimentar um circuito CMOS,
sabendo que a variação de tensão admitida no circuito é de 14,6V à 15,4V e que a potência consumida é de
pelo menos 5W calcule:
V1(ωt)=311sen(ωt); f=50Hz.
a)
b)
Calcule C, R e Icef.
Calcule e especifique o transformador.
Solução:
a)
Considerando os valores de tensão admitidos no circuito tem-se a tensão de pico com 15,4V e
a tensão mínima de 14,6V. Assim
$f, 14,6
0,948
gh
15,4
(9.1)
6
6 156
i
75@
C
5
(9.2)
Pelo ábaco da figura 10.9 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi obtêm-se ωRC=48
Considerando que a tensão média no circuito seja de 15V e a potência de 5W, obtêm-se o valor da
resistência:
Assim
C
`
48
20,5$B
75.314,16
(9.3)
:j*A 3,1 15,4
3,1 i :j*A 0,64<
gh
75
(9.4)
Vpk=15,4V
(9.5)
Pelo ábaco da figura 10.10 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi se obtêm
E a tensão máxima no capacitor é a tensão máxima de ondulação permitida no circuito:
b)
À partir do ábaco da figura 10.29 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi
obtêm-se FP=0,42. Logo
BC C
C
5
iD
11,9 <
D
BC 0,42
(9.6)
Tensão de saída do transformador:
A tensão de saída do transformador é obtida através do valor de pico necessário no circuito:
15,4
√2
10,9
(9.7)
Tensão de entrada do transformador
A tensão de entrada do transformador é obtida através do valor da fonte de entrada do circuito.
f, 311
√2
220
(9.8)
18
V1(ωt)= √2 127sen(ωt); f=60Hz; R=10Ω.
10.
Para o retificador com filtro capacitivo da figura abaixo, onde:
D1
D2
V1(ωt)
C
R
D3
D4
a)
Calcular e especificar o capacitor (C) para que a máxima ondulação de tensão na carga seja de
10% da tensão de pico de entrada.
Calcular a corrente eficaz neste capacitor.
b)
c)
Qual o fator de potência da estrutura?
Solução:
a)
Cálculo do capacitor:
Para que a máxima tensão de ondulação seja de 10%, sendo o pico de 179,61V diminui-se 10% do valor
de pico da tensão de entrada da fonte para obter a mínima tensão no capacitor que é de 161,64V. Assim
$f, 161,64
0,90
gh
179,61
(10.1)
Pelo ábaco da figura 10.9 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi obtêm-se ωRC=30.
Logo
`
b)
30
7,96$B
10 377
(10.2)
Corrente eficaz no capacitor:
:j*A 2,7 179,61
2,7 i :j*A 48,5<
gh
10
Pelo ábaco da figura 10.10 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi obtêm-se
c)
FP=0,46
(10.3)
pelo ábaco da figura 10.29 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi obtêm-se
19
11.
Deseja-se usar o circuito como fonte de tensão média de 600V, dados
V1(ωt)=√2 220sen(ωt); V2(ωt)=√2 220sen(ωt-120°); V3(ωt)=√2 220sen(ωt+120°); f= 60Hz; ∆Vo=2%;
Pout=600W. Considere transformador Y-Y
a)
b)
Calcular e especificar o capacitor (capacitância, corrente eficaz e máxima tensão).
Calcular e especificar o transformador (tensão eficaz de entrada e saída e potência(VA))
Solução:
a)
Como se deseja uma tensão média de 600V e uma ondulação máxima de 2%, considera-se
que seja 1% acima e 1% abaixo. Logo
$f, 594
0,98
606
gh
(11.1)
Cálculo da capacitância:
Pelo ábaco da figura 10.22 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi obtêm-se ωRC=35
6
6 6006
i
600@
C
600
A resistência da carga se obtêm através da seguinte expressão:
Logo
C
`
35
154,73kB
600 377
(11.2)
(11.3)
Cálculo da corrente no capacitor:
Pelo ábaco da figura 10.24 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi se obtêm
:j*A 2,14 606
2,14 i :j*A 2,16<
gh
600
(11.4)
A tensão de pico do capacitor será tensão de pico estabelecida para a carga
Vpk=606V
b)
(11.5)
Cálculo do transformador
Através do ábaco da figura 10.34 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi se obtêm
FP=0,42
Assim a potência do transformador é obtida conforme a seguir
BC C
C
600
iD
1428,57<
D
BC 0,42
(11.6)
20
Cálculo da tensão de saída:
Cálculo da tensão de entrada
f, 606
√2√3
247,4
√2. 220
√2
(11.7)
220
(11.8)
12.
Considere o retificador trifásico com ponto médio da figura abaixo. Sabe-se que o diodo D1
está queimado (aberto) e que:
V1(ωt)=√2 220sen(ωt); V2(ωt)=√2 220sen(ωt-120°); V3(ωt)=√2 220sen(ωt+120°); f= 60Hz; R=5Ω; L=3H;
D1=D2=D3=SKN 20/04, rt= 11mΩ, Vto=1V; Ta=40°C.
V1(ωt)
D1
V2(ωt)
D2
R
V3(ωt)
D3
L
Traçar as formas de onda V1, V2, V3, VL, IL e VD2.
a)
Calcular VLmed, ILmed, ILef, VD2, IDmed, IDef.
b)
c)
Calcular o valor da resistência térmica entre junção e o ambiente para que o diodo D2 se
mantenha com uma temperatura de junção inferior à 150°C.
Solução:
a)
Formas de onda
Verificação condução contínua
Devido a presença do diodo queimado, é necessário que a constante de tempo seja suficientemente
grande para que a corrente na carga não se anule durante um período 60° , que é o período em que se aplica
tensão negativa na carga, sendo assim ωc=π/3rad
"
5Q l
#
5Q l
3
#
5 l
(12.1)
3
3
#
5 l
5 3 377
3 l 2,78$
É condução contínua
21
V1(ωt)
400V
V2(ωt)
V3(ωt)
0V
-400V
400V
VL
0V
-400V
0V
VD2
-250V
-500V
40A
IL
30A
20A
10A
0A
b)
2π
π
0
3π
4π
Cálculo da tensão média na carga VLmed:
()*+
46
,
- √2 . /,012
2#
45
(12.2)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo.
()*+
598°
2
- 311 /,012 171,53
2#
mH8°
()*+ ; 171,53
34,30<
5
Cálculo da corrente eficaz na carga ILef:
(12.3)
Cálculo da corrente média na carga ILmed:
:()*+ (12.4)
Como a condução é contínua, com 5τ maior que o tempo em que a carga é submetida a tensão negativa
o suficiente para considerar a corrente na carga uma constante. Então:
:(*A :()*+ 34,30<
(12.5)
XY √2 √3 8 √2 √3 220 538,88
(12.6)
Cálculo da tensão de pico de D2 VD2:
Cálculo da corrente média no diodo:
Neste circuito cada diodo conduz em 1/2 do tempo total do ciclo. Então:
:X)*+ :()*+ 34,30
17,15<
2
2
(12.7)
22
Cálculo da corrente eficaz no diodo:
:X*A
c)
J
:(*A 34,30
1
T
-0:(*A 16 2 24,26<
2. #
√2
√2
(12.8)
8
Resistência junção ambiente
Cálculo da potência dissipada no diodo:
C Z :X*A 6 % [. :X)*+ 11$ 24,266 % 1 17,15 23,62\
]^ ; ]_ 150 ; 40
4,66°`/\
C
23,62
(12.9)
Cálculo da resistência junção-ambiente:
^_ (12.10)
C
(12.11)
D
Cálculo da potência ativa fornecida por cada fonte:
A potência que cada fonte fornece ao circuito é a potência total dissipada no resistor de carga dividida
pelo número de fontes que fornecem energia ao circuito, que neste circuito devido a queima de um diodo,
apenas duas fontes fornecem energia ao circuito.
d)
Cálculo do fator de potência:
C
BC :(*A 6 5 34,306
2941,23\
2
2
(12.12)
D d :*A 220 24,26 5337,2<
Cálculo da potência aparente
BC (12.13)
C 2941,23
0,55
D
5337,2
(12.14)
13.
Considere o circuito abaixo, que se encontra com o diodo D1 queimado, com tensão eficaz de
linha de 380V.
R=2Ω; L=100mH; E=350V; f=60Hz;
V1(ωt
)
D1
D2
D3
R
V2(ωt
)
L
V3(ωt
)
E
D4
a)
b)
D5
D6
Traçar as formas de onda V1, V2, V3, VL, IL, ID2 e VD2.
Calcular VLmed, ILmed, ILef, ID2med, ID2ef.
23
Solução:
a)
Formas de onda
Devido a presença do diodo queimado, é necessário que a constante de tempo seja suficientemente
grande para que a corrente na carga não se anule durante o período em que se aplica tensão com menor valor
do que a fonte E na carga.
537,4·sen(ωt)=350
(13.1)
Θ1 = ωt = 40,64°
Sendo θ1 o ângulo em que a fonte de entrada torna-se maior do que a fonte E, e através das formas de
onda base para tensões de linha verifica-se que a falta de um diodo em ponte de Graetz implica num período
de 2.θ1 em que se tem a tensão da fonte de alimentação menor do que o da fonte E. Portanto
ωc=2.40,64°=81,28°=1,419 rad
"
5Q l
"
5 l
(13.2)
0,1 1,419
5
l
2
377
0,25 l 3,76$
Condução contínua
V1(ωt)
400V
V2(ωt)
V3(ωt)
0V
-400V
VL
500V
250V
0V
0V
VD2
-250V
-500V
100A
IL
ID2
50A
-10A
b)
2π
π
0
3π
4π
Cálculo da tensão média na carga VLmed:
()*+
46
,
- √2 . /,012
2#
45
(13.3)
24
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o
ângulo de fim de condução do diodo.
Pode-se
()*+
568°
568°
2
G - 538,89 /,012 % - 538,89 /,012 I 428,84
2#
8°
M8°
()*+ ; 428,84 ; 350
39,42<
2
Cálculo da corrente eficaz na carga ILef:
Cálculo da corrente média na carga ILmed:
:()*+ (13.4)
(13.5)
Como a condução é contínua, e o tempo de 5τ é maior o suficiente que o tempo em que as fontes de
entrada ficam com tensão menor que o da fonte E para considerar a corrente na carga uma constante. Então :
:(*A :()*+ 39,42<
(13.6)
Cálculo da corrente de pico de D1 VD1:
XY √2 √3 8 √2 380 537,4
(13.7)
Cálculo da corrente média no diodo:
Devido ao diodo queimado os diodos da parte superior conduzem em metade do período cada
enquanto os diodos da parte inferior conduzem um terço do periodo. Então:
Diodos superiores:
:X)*+ Diodos inferiores:
:X)*+ Cálculo da corrente eficaz no diodo:
Diodos superiores:
:X*A
Diodos inferiores:
:()*+ 39,42
19,71<
2
2
:()*+ 39,42
13,14<
3
3
J
:(*A 39,42
1
T
-0:(*A 16 2 27,87<
2#
√2
√2
:X*A 8
6J
H
:(*A 39,42
T 1
- 0:(*A 16 2 22,76<
2#
√3
√3
(13.8)
(13.9)
(13.10)
(13.11)
8
25
14.
Considere o conversor abaixo com:
V(ωt)=225sen(ωt); f=50Hz;R=2Ω; L=9mH; E=10V;N1/N2=9.
D1
R
N2
L
V(ωt)
N1
N2
E
D2
a)
b)
c)
d)
Calcular o ângulo de extinção da corrente, βc e definir o modo de condução.
Traçar as formas de onda V(ωt), I(ωt), VL(ωt), IL(ωt) e ID1.
Calcule o valor da tensão média, corrente média e da corrente eficaz na carga.
A potência pode ser calculada por VLmed.ILmed? Justifique.
Solução:
a)
Cálculo do ângulo de extinção de corrente β:
Devido a presença de fonte E na carga o ângulo de início de condução do diodo deixa de ser α=0° e
passa a ser o ângulo em que a fonte de entrada tem seu valor maior que o da fonte E, polarizando
positivamente o diodo dando início a condução.
25·sen(ωt)=10
α = Θ1 = ωt = 23,58°
a
√ 2 10
25
(14.1)
0,40
314,16 9$
cos 0,577 W 0,6
2
Através do ábaco de Puschlowski obtêm-se:
cos α=23,58°
a= 0,4
cosΦ=0,6
(14.2)
(14.3)
β= 200°
(14.4)
2#
% '
$
Para este circuito monofásico ponto médio tem-se m=2 e α= 23,58° logo,
(14.5)
Cálculo do ângulo crítico de extinção de corrente βc:
!" βc=180+23,58=203,58°
(14.6)
Neste circuito acontece um fato que deve ser levado em consideração, na obtenção do valor de β, existe
uma variação no valor de β que não pode ser calculada matematicamente. Esta variação decorre do fato de
que o ábaco de Puschlowski foi criado considerando que a tensão na carga se torna negativa, porém no circuito
de ponto médio no momento em que a tensão na carga ficaria negativa, o outro diodo entra em condução
forçando o bloqueio do diodo que estava em condução e coloca uma tensão positiva na carga porém ainda
menor que a fonte E. Esta mudança no valor de tensão causa uma variação na energia acumulada no indutor, o
que ocasiona uma variação no valor do ângulo de extinção de corrente, esta mudança pode fazer com que um
circuito onde se obtêm um valor de β pelo ábaco próximo ao de βc, mas menor, o que resultaria em condução
descontínua, na realidade possua uma condução contínua muito próxima a critica, que é o caso que será
considerado neste circuito.
26
b)
Formas de onda:
400V
V(ωt)
0V
-400V
40V
VL
0V
-40V
50V
VD1
0V
-50V
5.0A
IL
0A
-5.0A
0.5A
I(wt)
0A
-0.5A
c)
2π
π
0
3π
4π
Cálculo da tensão média na carga VLmed:
()*+
46
,
- √2 . /,012
2#
45
(14.7)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o
ângulo de fim de condução do diodo.
()*+
5O8°
2
- 25 /,012 15,91
2#
8°
()*+ ; 15,91 ; 10
2,96<
2
(14.8)
Cálculo da corrente média na carga ILmed:
:()*+ (14.9)
d)
A potência não pode ser calculada por VLmed·ILmed devido a forma de onda de corrente ser
ondulada, o que significa que há a presença de harmônicas que não podem ser desconsideradas nos
cálculos.Assim a potencia na carga deveria ser calculada através de
C :(*A 6 % :()*+
(14.10)
27
15.
Considere o conversor abaixo com o diodo D1 queimado e também não queimado:
R=5Ω; L=3H; E=62V; Vo=220; f=60Hz; rt=10mΩ, Vto=0,6V; Ta=30°C; Rca=46°C/W.
V1(ωt)
D1
V2(ωt)
D2
R
V3(ωt)
D3
L
D4
E
a)
b)
c)
d)
Calcule o ângulo de extinção da corrente, modo de condução e βc.
Traçar as formas de onda V1, V2, V3, VL, IL , VD2 e I2.
A tensão e corrente média na carga.
Calcule a temperatura na cápsula do diodo D2.
Para circuito sem diodo queimado:
Neste caso o diodo D4 nunca entrará em condução, pois nunca terá tensão negativa na carga.
Cálculo do ângulo de extinção de corrente β:
Devido a presença da fonte é necessário verificar se o ângulo em que a fonte de entrada torna-se maior
do que o do valor da fonte E é maior ou menor do que 30° a fim de verificar a influência da fonte E no início de
condução do diodo.
311·sen(ωt)=62
Θ1 = ωt = 11,50°
(15.1)
Como o ângulo em que a fonte de entrada ultrapassa o valor da fonte E é menor do que 30°(ângulo em
que uma fonte de entrada se torna a fonte com o maior valor de tensão do circuito forçando a condução do
diodo) se tem
a
α=30°.
√ 2 62
√2 220
0,2
377 3
cos 0
5
Através do ábaco de Puschlowski obtêm-se:
cos α=30° a= 0,2
cosΦ=0
2#
% '
$
β= 271°
(15.2)
(15.3)
(15.4)
(15.5)
Cálculo do ângulo crítico de extinção de corrente βc:
!" Para este circuito tem-se m=3 e α= 30° logo,
βc=120+30=150°
(15.6)
(15.7)
Como β>βc é condução contínua.
28
b)
Formas de onda
V1(ωt)
400V
V2(ωt)
V3(ωt)
0V
-400V
400V
VL
200V
0V
VD2
0V
-250V
-500V
40A
IL
ID2
20A
0A
c)
2π
π
0
4π3π
Cálculo da tensão média na carga VLmed:
()*+
46
,
- √2 . /,012
2#
45
(15.8)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o
ângulo de fim de condução do diodo.
()*+
598°
3
- 311 /,012 257,19
2#
H8°
()*+ ; 257,19 ; 62
39,03<
5
(15.9)
Cálculo da corrente média na carga ILmed:
:()*+ (15.10)
Cálculo da corrente eficaz na carga ILef:
Como a condução é contínua, e β é maior que βc o suficiente para considerarmos a corrente na carga
uma constante. Então :
:(*A :()*+ 39,03<
(15.11)
Cálculo da corrente de pico no diodo VD:
XY √2 √3 8 √2 √3 220 538,88
(15.12)
29
Cálculo da corrente média no diodo:
:()*+ 39,3
13,01<
3
3
No circuito trifásico o diodo conduz em 1/3 do tempo total do ciclo. Então:
:X)*+ Cálculo da corrente eficaz no diodo:
:X*A d)
6J
H
:(*A 39,03
T 1
- 0:(*A 16 2 22,53<
2#
√3
√3
(15.13)
(15.14)
8
Resistência junção ambiente
C Z :X*A 6 % [. :X)*+ 10$ 22,536 % 0,6 13,01 12,88\
Cálculo da potência dissipada no diodo:
]" ; ]_ "_ C i ]" "_ C % ]_ 46 12,88 % 30 622,48°`
(15.15)
Cálculo da temperatura de cápsula:
(15.16)
Com diodo queimado
a)
Devido a presença do diodo queimado não é possível obter β através do ábaco de
Puschlowski, então a verificação de condução contínua é obtida através da constante de tempo. Onde o ângulo
ωc será igual ao intervalo em que o valor das duas fontes de entrada que entregam energia ao circuito
encontram-se com tensão abaixo do valor da fonte E.
311·sen(θ1)=62
Θ1 = 11,50°
(15.17)
Com um diodo queimado a carga teria tensão negativa em um período de 60°. Assim para que a carga tenha
tensão menor que da fonte E:
ωc = 60°+2.11,50° = 83° = 1,45rad
"
5Q l
"
5 l
3 1,45
5 l
5 377
3 l 3,85$
(15.18)
É condução contínua
30
b)
Formas de onda
Deve ser lembrado que no momento em que a tensão na carga se torna negativa o diodo D4 entra em
condução criando roda-livre na carga
V1(ωt)
400V
V2(ωt)
V3(ωt)
0V
-400V
400V
VL
200V
0V
0V
VD2
-250V
-600V
40A
IL
ID2
20A
0A
c)
2π
π
0
3π
4π
Cálculo da tensão média na carga VLmed:
()*+
46
,
- √2 . /,012
2#
45
(15.19)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo.
()*+
598°
2
- 311 /,012 184,73
2#
8°
()*+ ; 184,73 ; 62
24,55<
5
(15.20)
Cálculo da corrente média na carga ILmed:
:()*+ (15.21)
Cálculo da corrente eficaz na carga ILef:
Sendo condução contínua, considera-se constante pois a constante de tempo é suficientemente maior
que o tempo em que as fontes de entrada estão com tensão menor que a fonte E na carga. Então:
:(*A :()*+ 24,55
(15.22)
Cálculo da corrente de pico dos diodos VDP:
XY √2 √3 8 √2 √3 220 538,88
(15.23)
31
Cálculo da corrente média no diodo:
:()*+ 24,55
12,28<
2
2
Neste circuito cada diodo conduz em 1/2 do tempo total do ciclo. Então:
:X)*+ Cálculo da corrente eficaz no diodo:
:X*A
d)
J
(15.24)
:(*A 24,55
1
T
-0:(*A 16 2 17,36<
2#
√2
√2
8
(15.25)
Resistência junção ambiente
C Z :X*A 6 % [. :X)*+ 10$ 17,366 % 0,6 12,28 10,38\
(15.26)
]" ; ]_ "_ C i ]" "_ C % ]_ 46 10,38 % 30 507,48°`
(15.27)
Cálculo da potência dissipada nos diodos:
Cálculo da temperatura na cápsula:
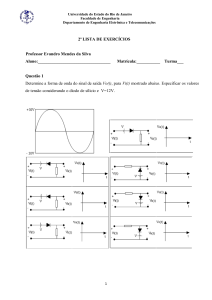
16.
Considere o conversor abaixo onde V(ωt)=220sen(ωt)
E=60V; L=100mH; R=5Ω; f= 50Hz
D
1
R
L
V(ωt)
E
Calcule o ângulo de extinção da corrente e defina o modo de condução.
a)
b)
Apresente as formas de onda e calcule VLmed e ILmed..
c)
Sendo E=0V e R= 20Ω, adicione em anti-paralelo com a carga um diodo e calcule o valor da
indutância para se obter condução crítica.
Solução:
a)
Cálculo do ângulo de extinção da corrente β:
Com a presença de fonte E na carga, o ângulo de início de condução do diodo deixa de ser α=0° e passa
a ser o ângulo em que a fonte de entrada tem seu valor maior que o da fonte E, polarizando positivamente o
diodo, dando início a condução.
220·sen(ωt)=60
α= Θ1 = ωt = 15,83°=0,276 rad
a
√ 2 cos 60
220
0,273 W 0,3
314,16 0,1
cos 0,157
5
(16.1)
(16.2)
(16.3)
32
Utilizando-se do ábaco de Puschlowski e aplicando médias sucessivas se obtêm os seguintes valores:
Para
Para
Para
a=0,2
a=0,4
a=0,3
cosΦ=0
β=274°
cosΦ=0,2
β=249°
cosΦ=0,1
β=261,5°
cosΦ=0,15
β=255,25°
cosΦ=0
(16.4)
β=236°
cosΦ=0,2
β=221°
cosΦ=0,1
β=228,5°
cosΦ=0,15
β=224,75°
cosΦ=0,15
β=240°=4,19 rad
2. #
% '
$
Onde m é o número de pulsos do conversor e α é o ângulo de início de condução do diodo.
Para este circuito tem-se m=1 e α= 15,83°.
Cálculo do ângulo crítico de extinção de corrente:
!" (16.5)
βc=360+15,83=375,83°
(16.6)
Como βc>β tem-se condução descontínua.
b)
Formas de onda:
V(ωt)
400V
0V
-400V
VL
400V
0V
-400V
0V
VD1
-200V
-400V
IL
8.0A
4.0A
0A
π
0
Cálculo da tensão média na carga VLmed:
()*+
46
3π
2π
4H
,
G - √2 . /,012 % - 2 I
2#
45
46
4π
(16.7)
33
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo (extinção da corrente β) e θ3 o ângulo de reinício de condução do diodo.
()*+
678°
1
G - 220 /,012 %
2·#
59,OH°
-
7,5N
602 I 73,83
()*+ ; 73,83 ; 60
2,77<
5
Indutância necessária para condução critica Lc:
Cálculo da corrente média na carga ILmed:
c)
6JK8,6LM
:()*+ (16.8)
(16.9)
Colocando um diodo em anti-paralelo, torna-se o circuito em um circuito monofásico de meia onda com
roda livre, onde para que haja condução critica é necessário que
#
5Q (16.10)
Onde π é o ângulo em que se tem roda livre, ou seja, é o tempo em que o indutor se descarregará
através do resistor até a fonte de entrada voltar a carregar o indutor. ω é a freqüência angular e τ é a constante
de tempo do circuito dada por L/R.
Portanto para que haja condução contínua é necessário que o tempo de 5τ seja maior que o tempo em
que a fonte fica sem fornecer energia à carga. Logo.
#. #. 20
40$S
5
5.314,16
(16.11)
17.
Para o retificador monofásico de onda completa com ponto médio abaixo.
R=2Ω; L=100mH; E=10V; V(ωt)=180sen(ωt); f=50Hz; rt=10mΩ; Vto=1V; Ta= 50°C; N1/N2=5
D
1
R
N
2
V(ωt)
L
N
1
N
2
E
D
2
a)
b)
c)
d)
Calcular o ângulo de extinção da corrente, βc e definir o modo de condução.
Traçar as formas de onda VL, IL, v(ωt), i(ωt) e VD1.
Calcular VLmed e ILmed.
Calcule a temperatura na cápsula do componente sendo que Rthjc=1°C/W, Rthca=45°C/W.
Solução:
a)
Cálculo do ângulo de extinção de corrente β:
Para circuitos monofásicos tem-se:
Devido a presença de fonte E na carga o ângulo de início de condução do diodo deixa de ser α=0° e
passa a ser o ângulo em que a fonte de entrada tem seu valor maior que o da fonte E, polarizando
positivamente o diodo dando início a condução.
36sen(ωt)=10
α =Θ1 = ωt = 16,13°=0,281 rad
√2 .
10
0,278 W 3
36
(17.1)
(17.2)
34
314,16 100$
cos 0,05 W 0
2
Através do ábaco de Puschlowski e fazendo médias sucessivas obtêm-se:
cos α=16,13°
a=0,2
a=0,4
a=0,3
cosΦ=0
cosΦ=0
cosΦ=0
β=274°
β=236°
β=255°
(17.3)
(17.4)
2#
% '
$
Cálculo do ângulo crítico de extinção de corrente βc:
!" (17.5)
Onde m é o número de pulsos do conversor e α é o ângulo de início de condução do diodo.
Para este circuito m=2 e α=16,13°.
logo,
βc=180+16,13°=196,13°
(17.6)
Como βc<β tem-se condução contínua.
b)
Formas de onda
200V
V(ωt)
0V
-200V
VL
40V
20V
0V
0V
VD1
-50V
-100V
10A
IL
0A
-10A
2A
I(wt)
0A
-2A
0
π
2π
3π
4π
35
c)
Cálculo da tensão média na carga VLmed:
()*+
46
,
G - √2 . /,012
2#
(17.7)
45
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o
ângulo de fim de condução do diodo.
()*+
5O8°
2
G - 36 /,012 22,87
2#
8°
(17.8)
Cálculo da corrente média na carga ILmed:
()*+ ; 22,87 ; 10
6,435<
2
Cálculo da corrente média no diodo:
:()*+ (17.9)
:()*+ 6,435
3,22<
2
2
Cada diodo conduz ½ do período total do ciclo:
:X)*+ Cálculo da corrente eficaz no diodo:
:X*A
d)
J
(17.10)
:(*A 6,435
1
T
-0:(*A 16 2 4,55<
2#
√2
√2
8
(17.11)
Resistência junção ambiente
C Z :X*A 6 % [. :X)*+ 10$ 4,556 % 1 3,22 3,4245\
Cálculo da potência dissipada no diodo:
]" ; ]_ "_ C i ]" "_ C % ]_ 45 3,4245 % 50 204,1°`
(17.12)
Cálculo da temperatura na cápsula do diodo:
18.
(17.13)
Para o retificador trifásico com ponto médio da figura abaixo.
V1(ωt)=√2 220sen(ωt); V2(ωt)=√2 220sen(ωt-120°); V3(ωt)=√2 220sen(ωt+120°); f= 60Hz; R=2Ω;
L=3000mH; E=100V; rt=10mΩ; Vto=1V; Ta=50°C.
V1(ωt)
D1
V2(ωt)
D2
R
V3(ωt)
D3
L
E
a)
Traçar as formas de onda VL(ωt), IL(ωt), ID2 e VD2.
b)
Calcular VLmed, ILmed, ILef, IDmed, IDef. e VDP.
c)
Calcular o fator de potência da fonte
d)
Calcular o valor da resistência térmica entre junção e o ambiente para que o diodo D1 se
mantenha com uma temperatura inferior a 150°C.
36
Solução:
a)
Formas de onda:
Cálculo do ângulo de extinção de corrente β:
Devido a presença da fonte é necessário verificar se o ângulo em que a fonte de entrada torna-se maior
do que o do valor da fonte E é maior ou menor do que 30° a fim de verificar a influência da fonte E no início de
condução do diodo.
311·sen(ωt)=100
(18.1)
Θ1 = ωt = 18,76°
Como o ângulo em que a fonte de entrada ultrapassa o valor da fonte E é menor do que 30°(ângulo em
que uma tensão de linha se torna a maior no circuito forçando a condução dos diodos) se tem
a
100
α=30°.
√ 2 311
(18.2)
0,321 W 0,3
(18.3)
377 3
cos 0
2
Através do ábaco de Puschlowski e fazendo médias sucessivas obtêm-se:
cos α=30°
a= 0,2
cosΦ=0
β= 274°
a= 0,4
cosΦ=0
β= 236°
a= 0,3
cosΦ=0
β= 255°
(18.4)
(18.5)
2#
% '
$
Para este circuito monofásico de meia onda tem-se m=1 e α= 30° logo,
Cálculo do ângulo crítico de extinção de corrente βc:
!" (18.6)
βc=120+30=150°
(18.7)
Como β >βc tem-se condução contínua.
V1(ωt)
400V
V2(ωt)
V3(ωt)
0V
-400V
400V
VL
200V
0V
0V
VD2
-250V
-500V
80A
IL
ID2
40A
0A
0
π
2π
3π
4π
37
b)
Cálculo da tensão média na carga VLmed:
()*+
46
,
- √2 . /,012
2#
45
(18.8)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo, θ2 é o
ângulo de fim de condução do diodo.
()*+
598°
3
- 311 /,012 257,19
2#
H8°
()*+ ; 257,19 ; 100
78,65<
2
Cálculo da corrente eficaz na carga ILef:
(18.9)
Cálculo da corrente média na carga ILmed:
:()*+ (18.10)
Como a condução é contínua, e β é maior que βc o suficiente para considerarmos a corrente na carga
uma constante. Então:
:(*A :()*+ 78,65<
(18.11)
Cálculo da corrente de pico de D1 VD1:
XY √2 √3 8 √2 √3 220 538,88
(18.12)
Cálculo da corrente média no diodo:
:()*+ 78,65
26,22<
3
3
No circuito trifásico, cada diodo conduz em 1/3 do tempo total do ciclo. Então:
:X)*+ Cálculo da corrente eficaz no diodo:
:X*A c)
6J
H
:(*A 78,65
T 1
- 0:(*A 16 2 45,41<
2#
√3
√3
8
Fator de potência:
BC C
D
C( :(*A 6 % :()*+ 2 78,656 % 100 78,65 20236\
Cálculo da potência ativa na carga:
C( 20236
6745,3\
3
3
Cálculo da potência aparente da fonte de tensão:
(18.13)
(18.14)
(18.15)
(18.16)
Mas como cada fonte contribui com 1/3 da potência total se tem:
Cb D *A :*A 220 45,41 9990,2<
Cálculo do fator de potência:
d)
BC Resistência junção ambiente:
6745,3
0,676
9990
C Z :X*A 6 % [. :X)*+ 10$ 45,416 % 1 26,22 46,84\
(18.17)
(18.18)
(18.18)
Cálculo da potência dissipada por diodo:
]^ ; ]_ ^_ C
(18.19)
Cálculo da resistência junção-ambiente
^_ ]^ ; ]_ 150 ; 50
2,135°`/\
C
46,84
(18.20)
(18.21)
38
19.
Considere o conversor abaixo com:
R=10Ω; E=180V; Vo=220.
V1(ωt)
D1
V2(ωt)
D2
R
V3(ωt)
D3
E
Traçar as formas de onda VL(ωt), IL(ωt), ID1 e VD1.
Calcular VLmed, ILmed, ILef, IDmed, IDef.
Calcular o fator de potência da fonte
a)
b)
c)
Solução:
a)
Formas de ondas
V1(ωt)
400V
V2(ωt)
V3(ωt)
0V
-400V
400V
VL
200V
0V
0V
VD1
-250V
-500V
20A
IL
10A
0A
π
0
b)
Calculo da tensão média na carga VLmed:
()*+
46
3π
2π
4H
,
G - √2 . /,012 % - 2 I
2#
45
4π
(19.1)
46
Onde n é o número de pulsos do conversor,θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo (extinção da corrente β) e θ3 o ângulo de reinício de condução do diodo.
39
311·sen(ωt)=180
Θ1 = ωt = 35,36°=0,617 rad
()*+
Θ2=ωt=180-35,36=144,64°=2,524 rad
(19.3)
Θ3=150+5,36=155,36°=2,712 rad
(19.4)
577,M7°
3
G 2#
H9,HM°
6,L56
311 /,012 % - 1802I 258,27
6,967
()*+ ; 258,27 ; 180
7,83<
10
Cálculo da corrente eficaz na carga ILef:
Cálculo da corrente média na carga ILmed:
:()*+ :(*A
(19.2)
577,M7°
46
,
3
√2 . /,01 ; 6
T
-0
1 2 T
2#
2#
45
H9,HM°
Cálculo da corrente média no diodo:
311 /,01 ; 180 6
0
1 2 9,03<
10
:()*+ 7,83
2,61<
3
3
(19.5)
(19.6)
(19.7)
No circuito trifásico o diodo conduz em 1/3 do tempo total do ciclo. Então:
:X)*+ Cálculo da corrente eficaz no diodo:
:X*A c)
Fator de potência:
6J
H
:(*A 9,03
T 1
- 0:(*A 16 2 5,21<
2#
√3
√3
8
BC C
D
C( :(*A 6 % :()*+ 10 9,036 % 180 7,83 2224,81\
Cálculo da potência na carga:
C( 2224,81
741,6\
3
3
(19.8)
(19.9)
(19.10)
(19.11)
Como cada fonte entrega 1/3 da potência total para a carga
Cb D *A :*A 220 5,21 1146,2<
(19.12)
Cálculo da potência aparente da fonte:
BC 741,6
0,647
1146,2
(19.13)
(19.14)
40
20.
Sabendo que a variação da tensão admitida no circuito é de 24V à 26V e que a potência
consumida pelo mesmo é 5W.
Vo= 220 V; f=60Hz
a)
Calcular e especificar o capacitor (C, Icef e Vmax)
b)
Calcular e especificar o transformador (tensão eficaz entrada, tensão eficaz de saída e
potência aparente).
Solução:
a)
Cálculo do capacitor
Como deseja-se uma tensão de pico de 26V e uma tensão mínima no capacitor de 24V tem-se:
$f, 24
0,923
26
gh
(20.1)
Pelo ábaco da figura 10.9 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi se obtêm ωRC=32
6
6 256
i
125@
C
5
A resistência pode ser obtida através da potência que é desejada pelo microprocessador. Assim
C
32
679,05kB
125.377
Calculo da corrente eficaz no capacitor:
Pelo ábaco da figura 10.10 do livro de Eletrônica de Potência 6 Edição de Ivo Barbi obtêm-se
Portanto,
`
:j*A . 2,8.26
2,8 i :j*A 0,58<
gh
125
(20.2)
(20.3)
(20.4)
A tensão máxima do capacitor deve ser a tensão máxima desejada no circuito, ou seja
Vpk=26
(20.5)
b)
Cálculo do transformador
Cálculo da potência aparente do transformador:
Através do ábaco figura 10.29 do livro de Eletrônica de Potência 6ª edição de Ivo Barbi se obtêm
FP=0,45, portanto
BC C
C
5
iD
11,11 <
D
BC 0,45
26
Cálculo da tensão de saída do transformador:
√2
Cálculo da tensão de entrada do transformador
18,38
f, 220
(20.6)
(20.7)
(20.8)
41
21.
Considere a estrutura abaixo onde f=60Hz, rt=11mΩ, Vto=0,85V, Rthjc=2°C/W e Rthcd = 1°C/W,
Ta= 50°C. V1(ωt)=√2 110sen(ωt); V2(ωt)=√2 110sen(ωt-120°); V3(ωt)=√2 110sen(ωt+120°); L=130mH e R=10Ω.
D
1
V1(ωt
)
D
2
D
3
R
V2(ωt
)
L
V3(ωt
)
D
4
D
5
D
6
a)
Calcule o valor da tensão média na carga e da corrente média na carga.
b)
Determine o valor da resistência térmica do dissipador para um dos diodos para que a
temperatura de junção se mantenha em 140°.
Caso o diodo D6 esteja com problemas (circuito aberto), esboce a forma de onda de tensão
c)
na carga e calcule o valor médio da tensão na carga.
Solução:
a)
Cálculo do ângulo de extinção de corrente β:
Para circuitos em ponte de Graetz tem-se:
a
α=60°.
?2√3
(21.1)
0
377 130$
cos 0,2
10
Através do ábaco de Puschlowski e fazendo médias sucessivas obtêm-se:
cos α=60° a= 0
cosΦ=0,2
β= 300°
(21.2)
(21.3)
(21.4)
2#
% '
$
(21.5)
βc=60+60=120°
(21.6)
Cálculo do ângulo crítico de extinção de corrente βc:
!" Para este circuito tem-se m=6 e α= 60° logo,
Como βc<β tem-se condução contínua.
42
Formas de onda
V1(ωt)
200V
V2(ωt)
V3(ωt)
0V
-200V
300V
VL
200V
100V
0V
0V
VD1
-200V
-400V
30A
IL
20A
10A
0A
π
0
Cálculo da tensão média na carga VLmed:
()*+
2π
3π
46
,
- √2 . /,012
2#
45
4π
(21.7)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução de um par de diodos, θ2
é o ângulo de fim de condução do par de diodos.
()*+
568°
6
- √3 √2 110 /,012 257,24
2#
M8°
()*+ ; 257,24
25,73<
10
Cálculo da corrente eficaz na carga ILef:
(21.8)
Cálculo da corrente média na carga ILmed:
:()*+ (21.9)
Como a condução é contínua, e β é maior que βc o suficiente para considerarmos a corrente na carga
uma constante. Então :
Cálculo da tensão de pico de D1 VD1:
:(*A :()*+ 25,73<
XY √2 √3 8 √2 √3 110 269,44
(21.10)
(21.11)
Cálculo da corrente média no diodo:
:()*+ 25,73
8,58<
3
3
No circuito trifásico o diodo conduz em 1/3 do tempo total do ciclo. Então:
:X)*+ (21.12)
43
Cálculo da corrente eficaz no diodo:
:X*A b)
6J
H
:(*A 25,73
T 1
- 0:(*A 16 2 14,86<
2#
√3
√3
(21.13)
8
C Z :X*A 6 % [. :X)*+ 11$ 14,866 % 0,85 8,58 9,71\
Cálculo da potência dissipada em um diodo
]^ ; ]_ ^_ . C
(21.14)
Cálculo da resistência junção ambiente:
^_ ^" % "+ % +_e
c)
(21.15)
]^ ; ]_
]^ ; ]_
140 ; 50
i +_e
; ^" ; "+e
; 2 ; 1 6,27°`/\
C
C
9,71
(21.16)
Verificação da condução
Verificando as formas de onda base, verifica-se que na falta de um diodo a tensão na carga não ficará
negativa, o que resultará no mínimo em condução critica, mas devido a presença do indutor pode se dizer que
terá condução contínua.
200V
V1(ωt)
V2(ωt)
V3(ωt)
0V
-200V
400V
VL
200V
0V
0V
VD1
-200V
-400V
40A
IL
20A
0A
Cálculo da tensão média na carga VLmed:
()*+
568°
2π
π
0
()*+
3π
4π
46
,
- √2 . /,012
2#
45
568°
2
G - 269,44 /,012 % - 269,44 /,012I 214,41
2#
8°
M8°
(21.17)
(21.18)
44
()*+ ; 214,41
21,44<
10
Cálculo da corrente média na carga ILmed:
:()*+ 22.
(21.19)
Seja o circuito :
D1
R
V1(ωt)
L
R= 100Ω; L=500mH; Vo=220V; f=60Hz.
Calcular
a)
Tensão média na carga
b)
Corrente média na carga
c)
O valor da corrente instantânea de carga quando ωt=π, no 1° semi-periodo.
d)
Verificar se a condução é contínua ou descontínua.
Solução:
a)
Cálculo da tensão média na carga VLmed:
()*+
46
,
- √2 . /,012
2#
45
(22.1)
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução do diodo D1, θ2 é o
ângulo de fim de condução do diodo D1 e entrada em condução do diodo de roda livre.
()*+
5O8°
1
- 311 /,012 99,0
2#
8
()*+ ; 99
0,99<
100
c)
Valor da corrente instantânea de carga quando ωt=π no primeiro semi-periodo:
sabe-se que a formula da corrente no tempo para circuitos rl é dada por
b)
Cálculo da corrente média na carga ILmed:
:()*+ f( 0#1 Onde,
mZ
√2 .
G
/,0# ; o1 ; /,0;o1/ p I
>
> ?6 % 0 16 213,38@
mZ
Assim
(22.2)
f( 0#1 4
377.0,5
62°
100
Jr
J588
/ p / qp / q( / HLL8,9 / m5,MM 0,189
√2 220
G
/,0# ; 62°1 ; /,0;62°1 0,189I 1,53<
213,38
(22.3)
(22.4)
(22.5)
(22.6)
(22.7)
(22.8)
45
d)
Verificação condução contínua
Como o circuito permanece em roda livre por π rad, tem-se ωc=π. Logo,
"
5Q l
#
5Q l
#
5 l
0,5
#
5
l
100 377
25$ l 8,33$
(22.9)
Assim verifica-se que é condução contínua e pelos valores obtidos pode-se dizer que é contínua
ondulada.
400V
V (ωt)
0V
-400V
400V
VL
200V
-10V
0V
VD1
-200V
-400V
2.0A
IL
1.0A
0A
3π
2π
π
0
4π
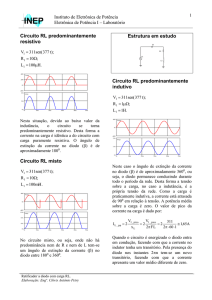
23.
Seja o retificador mostrado abaixo, onde V1=100V (pico); R= 10Ω e L=0,01H; f=60Hz. Calcular
VLmed, ILmed., potência absorvida pela carga e o FP da estrutura.
D1
R
V1(ωt)
L
46
Solução:
Cálculo do ângulo de extinção de corrente β:
Para circuitos monofásicos tem-se:
Ângulo de início de condução α= 0
a
√2 0
(23.1)
377 0,01
I cos 0,94
10
Através do ábaco de Puschlowski obtêm-se com:
cos G α=0
a= 0
cosΦ=0,9
β=206°
cosΦ=1,0
β=180°
(23.2)
(23.3)
Fazendo uma média obtêm-se
α=0
a= 0
cosΦ=0,95
β=193°
2#
% '
$
Onde m é o número de pulsos do conversor e α é o ângulo de início de condução do diodo.
Cálculo do ângulo crítico de extinção de corrente βc:
!" (23.4)
Para circuito monofásico de meia onda tem-se α=0 e m=1.
Βc=360°
(23.5)
Como βc>β tem-se condução descontínua.
Formas de onda:
100V
V(ωt)
0V
-100V
100V
VL
0V
-100V
0V
VD1
-50V
-100V
10.0A
IL
5.0A
0A
0
π
2π
3π
4π
47
Cálculo da tensão média na carga VLmed:
()*+
46
,
- √2 . /,012
2#
(23.6)
45
Onde n é o número de pulsos do conversor, θ1 é o ângulo de início de condução e θ2 é o ângulo de fim
de condução do diodo.
()*+
5NH°
1
- 100 /,012 31,42
2#
8
()*+ ; 31,42
3,14<
10
(23.7)
Cálculo da corrente média na carga ILmed:
Cálculo do fator de potência:
:()*+ (23.8)
Para o cálculo do fator de potência é necessário o valor da corrente eficaz na carga é na fonte de tensão,
que neste caso é o mesmo para os dois.
314,16 0,1
(23.9)
57,52°
20
Utilizando o ábaco da Fig.2.8 do livro de Eletrônica de Potência 6ª edição de Ivo Barbi para correntes
normalizadas obtêm-se:
Sendo
Portanto:
Ief=0,5A
(23.10)
> ?6 % 0 16 10,69@
(23.11)
:(*A Potência dissipada na carga:
√2 8 :*A 100 0,5
4,68<
>
10,69
(23.12)
P=R·ILef2
(23.13)
P=10·4,68²=218,9 W
Potência dissipada na fonte:
S=Vef·Ief
(23.14)
C
218,9
0,66
D 330,93
S=70,71·4,68=330,93 VA
BC (23.15)
24.
Considere o retificador trifásico com ponto médio da figura abaixo. Sabe-se que o diodo D1
está queimado (aberto) e que:
V1(ωt)=√2 220sen(ωt); V2(ωt)=√2 220sen(ωt+120°); V3(ωt)=√2 220sen(ωt-120°); f= 60Hz; R=10Ω;
L=800mH; D1=D2=D3=SKN 20/04, rt= 11mΩ, Vto=1V; Ta=30°C.
V1(ωt)
D1
V2(ωt)
D2
R
V3(ωt)
D3
L
48
a)
Traçar as formas de onda V1, V2, V3, VL, IL e VD2.
b)
Calcular VLmed, ILmed, ILef, VD1, IDmed, IDef.
c)
Calcular o valor da resistência térmica entre junção e o ambiente para que o diodo D2 se
mantenha com uma temperatura de junção inferior à 150°C.
Solução:
a)
Formas de onda
Verificação condução contínua
Devido a queima de um diodo a carga fica exposta a uma tensão negativa durante um tempo de 60°,
portanto ωc=60°=π/3 rad
"
5Q l
#
5 l
3. (24.1)
0,8
#
l
5
10 3 377
0,4 l 2,78$
É condução contínua
V1(ωt)
400V
V2(ωt)
V3(ωt)
0V
VL
400V
VL
0V
-400V
0V
VD2
-250V
-500V
20A
IL
10A
0A
0
b)
2π
π
3π
4π
Cálculo da tensão média na carga VLmed:
()*+
46
,
- √2 . /,012
2#
45
(24.2)
49
Onde n é o número de pulsos do conversor,θ1 é o ângulo de início de condução do diodo, θ2 é o ângulo
de fim de condução do diodo.
()*+
598°
2
- 311 /,012 171,53
2#
mH8°
()*+ ; 171,53
17,15<
10
Cálculo da corrente eficaz na carga ILef:
(24.3)
Cálculo da corrente média na carga ILmed:
:()*+ (24.4)
Como a condução é contínua, e a constante de tempo é grande o suficiente para considerarmos a
corrente na carga uma constante. Então :
Cálculo da tensão de pico de D2 VD2:
:(*A :()*+ 17,15<
XY √2 √3 8 √2 √3 220 538,88
(24.5)
(24.6)
Cálculo da corrente média no diodo:
:()*+ 17,15
8,575<
2
2
Neste circuito o diodo conduz em 1/2 do tempo total do ciclo. Então:
:X)*+ Cálculo da corrente eficaz no diodo:
:X*A
c)
J
:(*A 17,15
1
T
-0:(*A 16 2 12,13<
2#
√2
√2
8
C Z :X*A 6 % [. :X)*+ 11$ 12,136 % 1 8,575 10,19\
(24.7)
(24.8)
Cálculo da potência dissipada no diodo:
]^ ; ]_ 150 ; 30
11,78°`/\
C
10,19
(24.9)
Cálculo da resistência junção-ambiente
^_ (24.10)
50