Q - Tolstenko

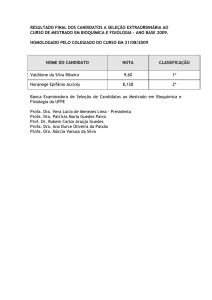
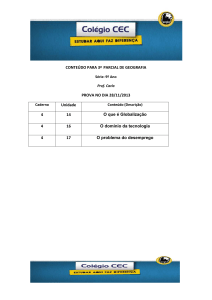
Capítulo 4: Análise de Sistemas:
1ª e 2ª Leis da Termodinâmica
Revisão
Exercícios
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Primeira lei da termodinâmica
• O balanço de energia pode ser escrito na forma
diferencial:
dE = δQ - δW
• Como energia E é uma propriedade termodinâmica,
sua integral não depende do caminho:
– Depende só do estado inicial e final do sistema.
E2 − E1 =1 Q2 −1W2
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Energia total do sistema
• A propriedade E representa toda a energia contida
em um sistema num determinado estado e será
considerada apenas as influências da energia
interna, energia cinética e energia potencial.
E = Energia interna(U ) + Energia cinética( Ec ) + Energia potencial ( Ep )
1
Ec = Mv 2
2
Ep = Mgz
onde: v = velocidade do sistema
g = aceleração gravitacional
z = elevação do sistema a partir de um referencial
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Energia Interna (U)
• A energia interna refere-se à energia que a molécula
possui como resultado dos movimentos de
translação, rotação e vibração em nível
microscópico.
• A energia interna está associada ao estado
termodinâmico do sistema e seus valores são
tabelados em função deste.
• Pode ser obtida através de equação de estado ou
através da tabela termodinâmica.
• Na região de saturação uma mistura líquido-gás
terá:
u = ul + x(ug – ul)
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Primeira lei da termodinâmica
• Há muitos processos reais que dependem
do tempo.
• Se as propriedades mudam a uma pequena
taxa em relação ao tempo, a hipótese de
processo quase-estático é válida:
Onde: dE
•
•
dE
= Q −W
dt
dt
= variação da energia total
•
Q = taxa de transferência de calor
•
W = potência
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Alguns casos particulares da
aplicação da primeira lei
• Num sistema isolado não há interação
com as imediações e desta forma:
1
Q2 = 0
e
W2 = 0
1
• Assim:
E 2 = E1
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Alguns casos particulares da
aplicação da primeira lei
• Em sistemas estacionários não há
movimentação do sistema como um todo
(ou são desprezíveis) e por isto:
∆Ec = 0
Logo:
e ∆ Ep = 0
dE = dU
• Integrando a primeira lei tem-se:
U 2 − U1 =1 Q2 −1W2
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Alguns casos particulares da
aplicação da primeira lei
• Processo de expansão quase-estático a
pressão constante (processo isobárico):
– Assumindo que o sistema seja estacionário e que o único
trabalho realizado durante o processo seja o associado
ao movimento da fronteira, a primeira lei da
termodinâmica se reduz a:
1Q2
1
- 1W2 = U2 – U1
Q2 = (U 2 + P2 V2 ) − (U 1 + P1 V1 )
1
Q2 = ∆(U + PV) = ∆H = H 2 - H 1
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Alguns casos particulares da
aplicação da primeira lei
• Processo de expansão quase-estático a pressão
constante (processo isobárico):
– Sendo ainda um gás ideal:
2
1
Q 2 = M ∫ c p dT
1
– Em sendo um gás perfeito: cp constante
1
EM-524 Fenômenos de Transporte
Q 2 = Mc p (T2 − T1 )
Profa. Dra. Carla K. N. Cavaliero
Alguns casos particulares da
aplicação da primeira lei
• Processo isotérmico reversível de um gás perfeito
em um sistema estacionário:
– No sistema estacionário: E = U
– No processo reversível:
δW = PdV
– No processo isotérmico de um gás ideal:
E conseqüentemente u = cte.
dE d ( Mu )
=
=0
1 Q2 − 1W 2 =
dT
dT
EM-524 Fenômenos de Transporte
1
T = cte
Q2 =1W2
Profa. Dra. Carla K. N. Cavaliero
Alguns casos particulares da
aplicação da primeira lei
• Processo adiabático reversível de um gás
perfeito em um sistema estacionário (processo
politrópico):
– No processo adiabático: δQ = 0
– No processo reversível: δW = PdV
– Para um gás ideal:
PV = MRgT
– Relação de propriedades:
P1  V2 
=  
P2  V1 
EM-524 Fenômenos de Transporte
γ
 P1 
 
 P2 
1- γ
 T2 
=  
 T1 
du = cv dT
dh = cp dT
cp – cv = Rg
γ
Profa. Dra. Carla K. N. Cavaliero
Primeira lei aplicada a um ciclo
• Quando um sistema perfaz um ciclo, o valor de
qualquer propriedade do sistema ao final é
idêntico ao seu valor no estado inicial. Portanto:
∫ dY = 0
onde Y é qualquer propriedade
• Como E é uma propriedade tem-se:
∫ dE = 0 = ∫ δQ − ∫ δW
• Logo:
∫ δQ = ∫ δW
Qciclo = Wciclo
O calor efetivo transmitido é igual ao trabalho efetivo realizado
para um sistema perfazendo um ciclo.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Enunciado de Clausius
É impossível construir um dispositivo que opere em
um ciclo termodinâmico e não produza outros
efeitos além da transferência de calor de um corpo
frio para um corpo quente
• Naturalmente, calor não pode fluir de um corpo à
temperatura mais baixa para outro à temperatura mais alta;
• Para a transferência de calor ocorrer neste sistema, devem
haver “outros efeitos”que o permitam.
• Por exemplo: a refrigeração de alimentos é realizada por
refrigeradores movidos a motores elétricos que necessitam
de trabalho de sua vizinhança para operar.
• Logo o enunciado de Clausius indica que é impossível
construir um ciclo de refrigeração que opere sem um aporte
de trabalho.
EM-524 Fenômenos de Transporte
Por Prof. Ricardo Mazza
Profa. Dra. Carla K. N. Cavaliero
Enunciado de Kelvin-Planck
É impossível construir um dispositivo que opere em
um ciclo termodinâmico e não produza outros
efeitos além da produção de trabalho e troca de
calor com um único reservatório térmico
• Calor não pode ser convertido em trabalho completamente e
continuamente em um único reservatório térmico operando
em um ciclo termodinâmico;
• A experiência mostra que o processo reverso é o processo
natural: trabalho pode ser completa e continuamente
convertido em calor.
EM-524 Fenômenos de Transporte
Por Prof. Ricardo Mazza
Profa. Dra. Carla K. N. Cavaliero
Máquina térmica
• É um dispositivo que opera num ciclo termodinâmico
e que produz trabalho líquido positivo, trocando calor
líquido também positivo.
• Um exemplo é o utilizado em grandes centrais de
geração elétrica para produção de potência elétrica.
EM-524 Fenômenos de Transporte
Por Prof. Ricardo Mazza
Profa. Dra. Carla K. N. Cavaliero
Máquina térmica
Reservatório de alta
temperatura
TH
QH
Máquina térmica
QL
Reservatório de baixa
temperatura
TL
∫ dE = 0 = ∫ δQ − ∫ δW ⇒ Q
ciclo
Q H − Q L = Wciclo
• Eficiência é a relação
W = Wlíq
do que se obtém pelo
que se gasta:
W
QH − QL
QL
η=
=
= 1−
QH
QH
QH
•
η=
EM-524 Fenômenos de Transporte
= Wciclo
W
•
QH
•
=
•
QH − QL
•
QH
•
= 1−
QL
•
QH
Profa. Dra. Carla K. N. Cavaliero
Sistema de refrigeração
Reservatório de alta
temperatura
TH
QH
Máquina térmica
revertida
QL
Reservatório de baixa
temperatura
TL
EM-524 Fenômenos de Transporte
• Seu objetivo é remover o calor
de um reservatório de baixa
temperatura.
• O coeficiente de desempenho
ou de eficácia de um
refrigerador pode ser escrito
W
como:
QL
QL
1
βR =
=
=
W
QH − QL  QH 

 − 1
 QL 
Por Prof. Ricardo Mazza
Profa. Dra. Carla K. N. Cavaliero
Bomba de calor
Reservatório de alta
temperatura
TH
QH
Máquina térmica
revertida
QL
W
• Como o objetivo é fornecer
calor a um reservatório de
alta temperatura, seu
coeficiente de desempenho
será (β
βBC):
β BC
QH
QH
=
=
=
W QH − QL
Reservatório de baixa
temperatura
TL
EM-524 Fenômenos de Transporte
Por Prof. Ricardo Mazza
1
 QL
1 − 
 QH



Profa. Dra. Carla K. N. Cavaliero
Processos ideais ou reversíveis
• Devido à segunda lei, nenhuma máquina térmica
pode apresentar teoricamente rendimento de
100%. O maior rendimento será o obtido de uma
máquina térmica reversível.
• No entanto, na prática não existem máquinas
reversíveis.
• Nos casos reais, existem várias causas de
irreversibilidade.
• Um ciclo externamente reversível é aquele em que
todos os processos são externamente reversíveis.
Um exemplo é o Ciclo de Carnot.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Ciclo de Carnot
• A máquina térmica que
opera num Ciclo de Carnot
consiste em 4 processos
externamente reversíveis:
– Processo isotérmico reversível
de transferência de calor, QH,
do reservatório TH para o
sistema;
– Um processo adiabático
reversível de abaixamento de
temperatura (TH→TL);
– Processo isotérmico reversível
de transferência de calor, QL, do
sistema ao reservatório TL;
– Um processo adiabático
reversível de aumento de
temperatura (TL→TH).
EM-524 Fenômenos de Transporte
Reservatório Quente TH
QH
Gerador de Vapor
Bomba
Turbina
W
Condensador
QL
Reservatório Frio TL
Profa. Dra. Carla K. N. Cavaliero
Ciclo de Carnot
TL =
máquina térmica: o
sistema realiza trabalho
EM-524 Fenômenos de Transporte
TL =
Bomba de calor e
refrigerador: o sistema
realiza trabalho
Profa. Dra. Carla K. N. Cavaliero
Escala termodinâmica de
temperatura
• Como a razão das transferências de calor em um
ciclo de potência reversível depende apenas das
temperaturas dos reservatórios, existirá uma escala
de temperatura independente das propriedades de
qualquer substância.
• Esta escala é denominada Escala Kelvin e expressa:
 QL

 QH
EM-524 Fenômenos de Transporte

 TL 

=  
 ciclo  TH  ciclo
Profa. Dra. Carla K. N. Cavaliero
Eficiência do ciclo de Carnot
• Assim, todas as máquinas térmicas externamente
reversíveis operando entre dois reservatórios possuem a
eficiência máxima:
η Carnot
W
QH − QL
QL
TL
= 1−
= 1−
=
=
QH
QH
QH
TH
η máx
TL
= 1−
TH
• Em bombas de calor e refrigeradores o coeficiente de
desempenho máximo será:
β Rmáx
QL
QL
TL
=
=
=
W
Q H − Q L TH − TL
EM-524 Fenômenos de Transporte
β BCmáx
TH
=
TH − TC
Profa. Dra. Carla K. N. Cavaliero
Segunda lei da termodinâmica:
Desigualdade de Clausius
Para uma máquina reversível:
Prova que a
δQ ≥ 0
=0
Desigualdade de
T
Clausius é
Para uma máquina térmica irreversível: válida para
δQ
QUALQUER
δQ ≥ 0
<0
máquina térmica
T
(reversível ou
Desigualdade de Clausius para
irreversível)
qualquer máquina:
∫
∫
∫
∫
δQ
 δQ 
∫  T  ≤ 0
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Entropia
• Desta forma, define-se entropia em processos
reversíveis como sendo:
 δQ 
dS ≡ 

 T  rev
onde:
δQ é a transferência de calor para (+) ou do (-) sistema;
T é a temperatura absoluta do sistema.
• A variação de entropia de um sistema entre um
estado e outro pode ser obtida como:
2
 δQ 
∆S = S 2 − S1 = ∫ 

T  rev
1
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Entropia de uma substância pura
• Os valores da entropia
específica podem ser
obtidos de forma
similar às outras
propriedades:
S
s=
M
• Para a região de
saturação o título deve
ser usado para se
calcular a entropia.
s = sl + x( sv − sl )
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Variação de entropia no ciclo de
T
Carnot
2
SSSS
1111
2222
SSSS
TH
−
1
1Q2
=
δQ
=
TH ∫1
TH
1
2
Área = Trabalho
líquido do ciclo
0000
3
∫
S3 −
− S 2 == ∫
2222
3333
SSSS
=
Processo adiabático
reversível
SSSS
4444
SSSS
1111
SSSS
−
Processo isotérmico reversível
2
2
3 Processo isotérmico reversível
4
TL
δδQ
Q
== 00
T
T
4
3333
SSSS
4444
SSSS
−
1
3 Q4
=
δQ =
∫
TL 3
TL
Wliq
área 1 - 2 - 3 - 4 - 1
η =
=
QH área 1 - 2 - b - a - 1
a
EM-524 Fenômenos de Transporte
b
S
Profa. Dra. Carla K. N. Cavaliero
Variação de entropia
• Para um caso geral (processos reversíveis e
irreversíveis), pode-se escrever que:
dS ≥
δQ
T
2
ou
S 2 − S1 ≥ ∫
1
δQ
T
A variação de entropia em um processo irreversível
é maior que num reversível com o mesmo δQ e T;
• De forma genérica, pode-se escrever que:
dS =
δQ
T
+ δS ger
EM-524 Fenômenos de Transporte
onde
δSger = 0 Processo reversível
δSger > 0 Processo irreversível
Profa. Dra. Carla K. N. Cavaliero
O termo δSger
dS =
δQ
T
+ δS ger
• S de um sistema aumenta por adição de calor ou pela
presença de irreversibilidade.
• S de um sistema diminui apenas por remoção de calor.
• Todos os processos adiabáticos reversíveis são
isoentrópicos (∆
∆S=0, ou seja, S2=S1).
• Nem todos processos isoentrópicos são obrigatoriamente
adiabáticos reversíveis (a remoção de calor pode
compensar a irreversibilidade).
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Duas relações termodinâmicas
importantes
• Primeira equação TdS:
TdS = dU + PdV
Tds = du + Pdν
• Segunda equação TdS:
TdS = dH − VdP
Tds = dh −νdP
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Variação de entropia para um gás
perfeito
• Pela primeira equação TdS:
 T2 
 ν2 
s2 − s1 = c v cte ln  + R g ln 
 T1 
 ν1 
• Usando a segunda equação TdS:
 T2 
 P2 
s2 − s1 = cp cteln  − R g ln 
 T1 
 P1 
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Processo isentrópico para um gás
perfeito
• Da equação de estado para gases perfeitos e da de
processos politrópico, pode-se escrever que:
 P2   V1 
  =  
 P1   V2 
e:
 T2   P2 
  =  
 T1   P1 
EM-524 Fenômenos de Transporte
( γ −1)
γ
γ
 V1 
=  
 V2 
γ −1
Profa. Dra. Carla K. N. Cavaliero
Moto perpétuo
São considerados motos perpétuos os sistemas que
violam alguma lei termodinâmica.
• Moto perpétuo da 1ª. lei
– Um exemplo deste sistema pode ser um sistema
adiabático que fornece trabalho sem que haja mudanças
na energia interna, potencial ou cinética.
• Moto perpétuo da 2ª. lei
– Um exemplo seria uma máquina térmica que recebesse
calor de uma reservatório mais quente e realizasse
apenas trabalho (eficiência 100%).
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Exercícios - Capítulo 4
Análise de sistemas: 1ª e 2ª leis da
termodinâmica
Proposição de exercícios:
4.1/ 4.3/ 4.6/ 4.7E/ 4.8/ 4.10/ 4.13/4.14/ 4.15/
4.16/ 4.17/ 4.18/ 4.22/ 4.23/ 4.24/ 4.27/ 4.31/
4.32/ 4.34/ 4.37/ 4.38
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Exercício 1: Água contida em uma montagem pistão-cilindro é
submetida a dois processos em série partindo de um estado
inicial onde a pressão é 10 bar (1 MPa) e a temperatura é 400 oC:
Processo 1-2: a água é resfriada à medida que é comprimida à
pressão cte de 10 bar até o estado de vapor saturado;
Processo 2-3: a água é resfriada a volume cte até 150 oC.
Esboce os processos no diagrama T-ν
ν e determine o trabalho
(kJ/kg) e a quantidade de calor transferida (kJ/kg) para o
processo global.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Exercício 2: Vapor d’água saturado a 0,40 MPa é expandido
reversivelmente e adiabaticamente em um dispositivo pistãocilindro, atingindo a pressão de 0,10 MPa.
Esboce esse processo em um diagrama T-s.
Determine o título da água no estado final.
Considerando que as variações de energia cinética e potencial
são desprezíveis ao longo do processo, determine o trabalho
realizado (kJ/kg).
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Exercício 3: Uma central de potência opera hipoteticamente
segundo um ciclo de Carnot com água/vapor como fluido de
trabalho. A adição de calor isotérmica reversível ocorre em uma
caldeira à pressão de 2 MPa e, durante este processo, água líquida
saturada é convertida em vapor d’água saturado. A rejeição de
calor isotérmica reversível ocorre em um condensador à 1 atm.
a) Calcule a transferência de calor em cada etapa do ciclo.
b) Qual é o trabalho líquido realizado pela máquina?
c) Qual é a eficiência térmica da máquina? Compare este valor
com o valor máximo teórico. Ciclo de Carnot:
T
P=2MPa
TH=212,42 oC
TL=99,63 oC
1
4
2
P=0,1MPa
3
1-2: isotérmico reversível (TH)
2-3: adiabático reversível (isoentrópico)
3-4: isotérmico reversível (TL)
4-1: adiabático reversível (isoentrópico)
Pela 2a lei da termodinâmica:
δQ
EM-524 Fenômenos de Transporte
s
Q2
dS =
∴ s2 − s1 =
T
T
Profa. Dra. Carla K. N. Cavaliero
1
Exercício 4: O projeto da termoelétrica de Carioba II (AmericanaSP 2000) prevê uma geração de 950 MW queimando gás natural e
operando num ciclo Rankine (vapor) a uma pressão máxima de 6
MPa. Determine a mínima taxa de calor que ela rejeitará ao rio
Piracicaba. Se ela tomar do rio 4 m3/s de água para fins de
resfriamento, calcule qual o aumento na temperatura dessa água
ao retornar ao rio (considere desprezível esse aumento de
temperatura em função do tempo).
W=950 MW P=6MPa
Ciclo a vapor
TH=276oC (vapor saturado a 6 MPa)
TL=25oC
QL ?
Retirando 4 m3/s de água do rio, ∆T ?
EM-524 Fenômenos de Transporte
6MPa e 276oC
950 MW
oC Dra. Carla K. N. Cavaliero
25Profa.
Exercício 4: O projeto da termoelétrica de Carioba II (AmericanaSP 2000) prevê uma geração de 950 MW queimando gás natural e
operando num ciclo Rankine (vapor) a uma pressão máxima de 6
MPa. Determine a mínima taxa de calor que ela rejeitará ao rio
Piracicaba. Se ela tomar do rio 4 m3/s de água para fins de
resfriamento, calcule qual o aumento na temperatura desta água
ao retornar ao rio (considere desprezível esse aumento de
temperatura em função do tempo).
TH=276oC = 549K
ηCarnot
TL=25oC = 298K
TL
298
= 1−
= 1−
= 0,457
TH
549
•
ηCarnot
•
950
= • ⇒ QH =
= 2079MW
0,457
QH
•
W
•
•
QL = QH − W = 2079 − 950 = 1129 MW
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Exercício 4: O projeto da termoelétrica de Carioba II (AmericanaSP 2000) prevê uma geração de 950 MW queimando gás natural e
operando num ciclo Rankine (vapor) a uma pressão máxima de 6
MPa. Determine a mínima taxa de calor que ela rejeitará ao rio
Piracicaba. Se ela tomar do rio 4 m3/s de água para fins de
resfriamento, calcule qual o aumento na temperatura desta água
ao retornar ao rio (considere desprezível esse aumento de
temperatura em função do tempo).
TH=276oC = 549K
TL=25oC = 298K
Tomando água do rio a 4 m3/s, o aumento da temperatura será:
•
QL = Mc∆T
∆T =
QL
•
ρV c
Considerando ρ = 1000 kg/m3 e c = 4190 J/kg.K, tem-se
1129 ∗106
∆T =
= 67 K = 67 o C
1000 ∗ 4 ∗ 4190
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
FIM!
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero