1ª Lei da Termodinâmica - DEP

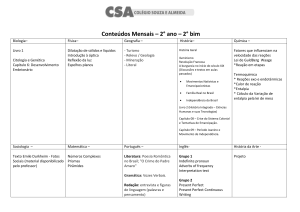
Capítulo 2. A 1ª Lei da Termodinâmica
Parte 2: termoquímica; entalpia de transformações físicas e
químicas; lei de Hess; entalpia padrão de formação; entalpia
padrão de reacção; sua dependência da temperatura
Baseado no livro: Atkins’ Physical Chemistry
Eighth Edition
Peter Atkins • Julio de Paula
22-03-2007
Maria da Conceição Paiva
1
Termoquímica
A termoquímica estuda a energia transferida na forma de calor durante as
reacções químicas.
O reactor, ou recipiente onde se dá a reacção, e o seu conteúdo,
constituem o sistema em estudo.
Pode-se usar a calorimetria para medir q para uma reacção, ou seja, para
medir
ΔU – se a reacção ocorrer a volume constante
ΔH – se a reacção ocorrer a pressão constante
Quando se liberta energia para o meio exterior durante a reacção química,
a pressão constante - ΔH ‹ 0 (processo exotérmico)
Quando se absorve energia do meio exterior durante a reacção química, a
pressão constante - ΔH › 0 (processo endotérmico)
22-03-2007
Maria da Conceição Paiva
2
Variações de entalpia padrão
ΔH0 – variação de entalpia para um processo em que os reagentes e
produtos se encontram nos seus estados padrão
Estado padrão de uma substância: estado de uma substância a
determinada temperatura e à pressão de 1 bar.
Ex: variação de entalpia padrão de vaporização para a H2O, ΔvapH0, é a
variação molar de entalpia do líquido puro a 1 bar, quando passa a gás,
a 1 bar.
H2O(l) → H2O(g)
ΔvapH0 (373 K) = +40.66 kJ/mol
Pode-se fornecer valore de entalpia padrão a qualquer temperatura. A
temperatura convencional para descrever quantidades termodinâmicas
é 298.15 K.
22-03-2007
Maria da Conceição Paiva
3
Entalpia de transformações físicas
As mudanças de estado físico são acompanhadas por variações de entalpia. Se estas
forem descritas à pressão de 1 bar, são definidas como transições de entalpia padrão.
Ex:
Entalpia padrão de vaporização, ΔvapH0 – variação de entalpia que acompanha a
conversão de líquido para gás
Entalpia padrão de fusão ΔfusH0 - variação de entalpia que acompanha a conversão de
sólido para líquido
22-03-2007
Maria da Conceição Paiva
4
A entalpia é uma função de estado, logo a
variação de entalpia é independente do
caminho percorrido entre o estado inicial e final
H2O(s) → H2O(l)
ΔfusH0
H2O(l) → H2O(g)
ΔvapH0
H2O(s) → H2O(g)
ΔsubH0= ΔfusH0 + ΔvapH0
ΔsubH0= 6.01 + 40.66 = 46.67 kJ/mol
22-03-2007
Maria da Conceição Paiva
5
ΔH0 (A→B)= - ΔH0 (B→A)
A entalpia padrão de um processo é igual e de sinal oposto à entalpia padrão do
processo inverso.
22-03-2007
Maria da Conceição Paiva
6
22-03-2007
Maria da Conceição Paiva
7
Entalpia de reacção química
2 A + B → 3C + D
Entalpia padrão de reacção:
Δr H 0 =
0
ν
H
∑ m−
produtos
0
ν
H
∑ m
reagentes
Ou seja, para a reacção anterior, a entalpia padrão de reacção será:
{
} {
}
Δ r H 0 = 3H m0 (C ) + H m0 (D ) − 2H m0 (A ) + H m0 (B )
Ex: entalpia padrão de combustão do metano
CH4 (g) + 2 O2 (g) → CO2 (g) + 2 H2O (l)
ΔcH0= (ΔfH0CO2 + 2ΔfH0H2O) - (ΔfH0CH4 + 2ΔfH0O2) = (-393.51-(2x285.83)) – (-74.8+0) kJ/mol
ΔcH0= - 890.37 kJ/mol
22-03-2007
Maria da Conceição Paiva
8
22-03-2007
Maria da Conceição Paiva
9
Lei de Hess
A entalpia padrão de uma reacção pode ser obtida a partir das entalpias padrão de
reacções individuais em que a reacção principal se possa dividir.
Exemplo: a partir da entalpia padrão de hidrogenação do propeno e da entalpia padrão
de combustão do propano, calcule a entalpia padrão de combustão do propeno.
CH2=CH-CH3 (g) + H2 → CH3CH2CH3 (g)
ΔHH0= -124 kJ/mol
CH3CH2CH3 (g) + 5 O2 → 3 CO2 (g) + 4 H2O (l)
ΔCH0= -2220 kJ/mol
H2O (l) → H2 (g) + ½ O2 (g)
ΔrH0= +286 kJ/mol
CH2=CH-CH3 (g) + 9/2 O2 (g) → 3 CO2 (g) + 3 H2O (l)
ΔCH0 (propeno) = ΔCH0 (propano) + ΔHH0 (propeno) - ΔrH0 (água)
ΔCH0 (propeno) = -2220 – 124 + 286 = -2058 kJ/mol
22-03-2007
Maria da Conceição Paiva
10
Entalpia padrão de formação, ΔfH0
A entalpia padrão de formação, ΔfH0,
de uma substância, é a entalpia padrão
da reacção de formação dessa
substância a partir dos seus elementos
no seu estado padrão.
O estado de referência de um
elemento é o seu estado mais estável à
pressão de 1 bar e à temperatura
indicada.
As entalpias padrão de formação de
elementos no seu estado de referência
são zero, a qualquer temperatura.
22-03-2007
Maria da Conceição Paiva
11
22-03-2007
Maria da Conceição Paiva
12
Entalpia padrão de reacção – pode ser obtida a partir das entalpias padrão de
formação dos reagentes e produtos envolvidos nessa reacção
Pode-se considerara a reacção como
soma de duas etapas, a da decomposição
dos reagentes nos seus elementos e a
formação dos produtos a partir desses
elementos
Δr H 0 =
0
ν
Δ
H
∑ f −
produtos
0
ν
Δ
H
∑ f
reagentes
Em que ν é o coeficiente estequiométrico
22-03-2007
Maria da Conceição Paiva
13
Dependência da entalpia de reacção na temperatura
Quando não se dispõe dos valores experimentais da entalpia de uma reacção a
diferentes temperaturas, o seu valor pode-se estimar a partir do conhecimento da
entalpia da reacção a uma determinada temperatura e das capacidades caloríficas
de produtos e reagentes.
Quando uma substância é aquecida de T1 para T2, a sua entalpia varia (assumindo
que não há transições de fase na gama de temperatura considerada):
H (T2 ) = H (T1 ) + ∫ C p dT
T2
T1
Esta equação é aplicável a cada substância envolvida na reacção, logo:
Δ r H (T2 ) = Δ r H (T1 ) + ∫ Δ r C p0 dT
0
0
T2
Equação de Kirchhoff
T1
Em que:
Δ r C p0 =
0
ν
C
∑ p ,m −
produtos
22-03-2007
Maria da Conceição Paiva
0
ν
C
∑ p ,m
reagentes
14
Ilustração da equação de Kirchhoff
Δ r H 0 (T2 ) = Δ r H 0 (T1 ) + ∫ Δ r C p0 dT
T2
T1
22-03-2007
Maria da Conceição Paiva
15
As funções de estado, tais como a energia interna, U e a entalpia, H, são
propriedades que têm um valor que não depende da forma como a amostra é
preparada. O seu valor depende apenas do estado em que o sistema se
encontra, e não da história prévia do sistema.
Para um sistema que sofra as variações
indicadas na figura, desde o estado de
energia interna Ui até ao estado de energia
interna Uf, o trabalho realizado quando a
variação se efectua pelo caminho 1, por um
processo de expansão adiabática, será w. O
mesmo estado final pode ser atingido por
um processo de expansão não adiabática,
pelo caminho 2, e neste caso o sistema
realiza um trabalho w’. O estado de energia
interna Ui e Uf são os mesmos em ambos os
casos, mas no primeiro caso não há
variação de calor e a variação de energia,
na forma de trabalho, é diferente nos dois
processos.
22-03-2007
Maria da Conceição Paiva
16
Quando um sistema passa de um estado inicial Ui para um estado final Uf a
sua variação total é igual à soma (integral) de todas as variações
infinitesimais ao longo do caminho.
f
ΔU = ∫ dU
i
ΔU depende do estado inicial e final do sistema, mas não do caminho
percorrido entre eles.
dU é uma diferencial exacta: é uma quantidade infinitesimal que, quando
integrada, dá um resultado independente dos estados inicial e final.
22-03-2007
Maria da Conceição Paiva
17
A energia interna é uma função de V, T e p. Como é descrita por uma equação de
estado, estas variáveis estão relacionadas: conhecendo o valor de duas delas, o valor
da terceira fica definido.
Quando V varia para V+dV a T
constante, U varia para:
Quando T varia para T+dT a V
constante, U varia para:
⎛ ∂U ⎞
U' = U + ⎜
⎟ dT
∂
T
⎝
⎠V
⎛ ∂U ⎞
U' = U + ⎜
⎟ dV
⎝ ∂V ⎠T
22-03-2007
Maria da Conceição Paiva
18
Se V e T variarem ambos infinitesimalmente, a energia interna será dada pelas
somas das variações infinitesimais (desprezando as variações infinitesimais de 2ª
ordem, que correspondem a dVdT):
⎛ ∂U ⎞
⎛ ∂U ⎞
U' = U + ⎜
⎟ dT
⎟ dV + ⎜
V
T
∂
∂
⎠V
⎝
⎠T
⎝
= U + dU
⎛ ∂U ⎞
⎛ ∂U ⎞
dU = ⎜
⎟ dV + ⎜
⎟ dT
∂
V
∂
T
⎝
⎠T
⎝
⎠V
dU = π T dV + CV dT
(∂U/∂V)T – medida da variação da energia
interna de uma substância quando o seu
volume varia a temperatura constante - πT, ou
pressão interna
22-03-2007
Maria da Conceição Paiva
19
Para um gás perfeito, a energia interna é independente do volume (a T
constante). Não há interacção entre moléculas, logo a energia interna é
independente da distância entre moléculas, e portanto é independente do
volume da amostra. Então, πT= 0.
Num gás real, quando a energia
interna aumenta com a expansão
isotérmica do gás, πT> 0 (domínio
em que as moléculas sofrem
forças atractivas entre elas).
22-03-2007
Maria da Conceição Paiva
20
Experiência de Joule
Procurou medir πT medindo a varição de temperatura do gás na sua expansão no vazio.
Usou dois compartimentos metálicos imersos num banho de água. Procurou medir a
variação de temperatura do banho quando se dá a expansão do gás para o vazio. Não
encontrou variação de T, ou seja, concluiu que, como w=0, e q=0, então ΔU=0.
Na
verdade,
na
expansão
isotérmica de um gás, U varia
muito pouco, por isso πT ≈0. Nas
condições da experiência a
variação de T observada era
demasiado pequena
para ser
medida
22-03-2007
Maria da Conceição Paiva
21
Variação da energia interna a pressão constante
A partir da equação obtida anteriormente:
dU = π T dV + CV dT
Observa-se a variação com a T a pressão
constante como sendo:
⎛ ∂U ⎞
⎛ ∂V ⎞
π
=
⎜
⎟
⎟ + CV
T⎜
⎝ ∂T ⎠ p
⎝ ∂T ⎠ p
Declive do gráfico da variação de V com
T, a pressão constante → é o coeficiente
de expansão, α, da substância, ou seja, é
a fracção do volume que varia por
aumento de temperatura.
α=
22-03-2007
Podemos também definir um outro
coeficiente: a compressibilidade
isotérmica, κT, a fracção do
volume que varia devido a um
aumento de pressão a T constante.
1 ⎛ ∂V ⎞
⎟
⎜
V ⎝ ∂T ⎠ p
κT =
Maria da Conceição Paiva
1 ⎛ ∂V
⎜
V ⎜⎝ ∂p
⎞
⎟⎟
⎠T
22
Introduzindo α na expressão para (∂U/∂T)p, obtém-se:
⎛ ∂U ⎞
⎜
⎟ = απ TV + CV
⎝ ∂T ⎠ p
Para um gás perfeito, πT=0, logo:
⎛ ∂U ⎞
⎟ = CV
⎜
⎝ ∂T ⎠ p
Pode-se provar que:
C p − CV = nR
α 2TV
C p − CV =
κT
22-03-2007
Maria da Conceição Paiva
23
Problemas
6. Uma amostra constituída por 1 mole de átomos de gás perfeito
(para os quais Cv,m = 3/2 R) sofre o ciclo descrito na figura ao
lado.
a)Determine a temperatura nos pontos 1, 2 e 3
b)Calcule q, w, ΔU e ΔH para cada passo e para o ciclo total
Se a informação disponível não permitir uma resposta numérica,
indique se é +, -, 0 ou ?, conforme apropriado.
7. Uma amostra de 1.00 mole de H2O (g) foi condensada isotermicamente e reversivelmente a
água líquida a 100 ºC. A entalpia padrão de vaporizaçãoda água a 100 ºC é 40.656 kJmol-1.
Calcule w, q, ΔU e ΔH para este processo.
8. Quando se fornece 229 J de energia na forma de calor a 3.0 moles de Ar (g), a temperatura da
amostra aumenta de 2.55 K. Calcule as capacidades caloríficas molares a volume constante e
pressão constante para este gás.
9. Dadas as reacções (1) e (2), determine: a) ΔrH0 e ΔrU0 para a reacção 3; b) ΔfH0 para HCl (g) e
H2O (g), ambos a 298 K.
(1)
H2 (g) + Cl2 (g) → 2 HCl (g)
ΔrH0 = -184.62 kJ mol-1
(2)
2 H2 (g) + O2 (g) → 2 H2O (g)
ΔrH0 = -483.64 kJ mol-1
(3)
4 HCl (g) + O2 (g) → 2 Cl2 (g) + 2 H2O (g)
10. Um determinado líquido tem ΔvapH0= 32.0 kJmol-1. Calcule q, w, ΔH e ΔU quando se vaporiza
0.75 mol a 260 K e 765 Torr. R: q= ΔH= 24.0 kJ; w= -1.6 kJ; ΔU= 22.4 kJ.
22-03-2007
Maria da Conceição Paiva
24
Problemas
11. Verificou-se que a capacidade calorífica a pressão constante de uma amostra de um gás perfeito
variava com a temperatura de acordo com a expressão: Cp= 20.17 + 0.4001 T (J/K-1). Calcule q, w,
ΔU e ΔH quando a temperatura aumenta de 0 ºC a 100 ºC (a) a pressão constante, (b) a volume
constante.
R: a) q= ΔH =13.1 x 103 J; w= -831 J; ΔU= 12.3 kJ; b) ΔH =13.1 kJ; w= 0; ΔU= q= 12.3 kJ
12. Quando 2 moles de CO2 são aquecidas a uma pressão constante de 1.25 atm, a sua
temperatura aumenta de 250 K para 277 K. Sendo a capacidade calorífica molar do CO2 a pressão
constante 37.11 JK-1mol-1, calcule q, ΔU e ΔH.
R: q= ΔH =2 x 103 J mol-1; ΔU= 1.6 x 103 J mol-1
13. Uma amostra de 5 moles de CO2 está inicialmente limitada a 15 dm3 a 280 K, sofrendo de
seguida uma expansão adiabática contra uma pressão constante de 78.5 kPa até o volume ter
aumentado 4 vezes. Calcule q, w, ΔT, ΔU e ΔH. (a pressão final do gás não é necessariamente 78.5
kPa). R: q=0; w=-3.5 kJ; ΔU=-3.5 kJ; ΔT=-24 K; ΔH=-4.5 kJ.
14. Dadas as reacções (1) e (2) abaixo, determine: a) ΔrH0 e ΔrU0 para a reacção (3) e b) ΔfH0 para o
HI (g) e para a H2O (g) a 298 K.
(1)H2 (g) + I2 (s) → 2 HI (g)
ΔrH0 = +52.96 kJ mol-1
(2)2 H2 (g) + O2 (g) → 2 H2O (g)
ΔrH0 = -483.64 kJ mol-1
(3)4 HI (g) + O2 (g) → 2 I2 (s) + 2 H2O (g)
R: a) ΔrH0 (3)= -589.56 kJ mol-1; ΔrU0 (3)= -582.13 kJ mol-1; b) ΔfH0 (HI) = 26.48 kJ mol-1; ΔfH0 (H2O)=
-241.82 kJ mol-1
22-03-2007
Maria da Conceição Paiva
25