Ciências
Natureza
Ciênciasda
Humanas
e
esuas
suasTecnologias
Tecnologias
Física
História
Prof. Marcos
Prof.: Haroldo
Zilfran
8
13
nº
nº
A Física Hopi Hari
MONTEZUM
Montezum é a maior montanha-russa de madeira da América
Latina e é a montanha-russa de madeira mais próxima de Jundiaí.
Também, pudera, sua extensão é de 1,2 quilômetro e ela se situa em
Vinhedo.
O tempo total de percurso da Montezum é de 1min 27seg, e
30seg desse tempo são gastos durante a subida inicial. Veja abaixo
uma foto da Montezum:
No ponto mais alto da Montezum (vide foto acima), o
carrinho de massa 7500kg é praticamente abandonado do repouso
e a energia mecânica dele é dada pela fórmula Em = Ep + Ec.
Acompanhe o cálculo abaixo:
•
Em = Ep + 0
•
Em = mgh + 0
•
Em = (7500).(10).(44) → h = 44m é a altura do ponto
mais alto.
•
Em = 3300000J
Como a Energia Mecânica se conserva por todo
o trajeto (estamos desconsiderando o atrito), podemos
calcular qual a velocidade máxima que o carrinho atinge.
Essa velocidade ocorre ao final da primeira descida. Observe:
•
Em = Ep + Ec
•
Em = 0 + (mv²)/2 (a energia potencial na parte mais
baixa é nula)
•
v² = [(2).(Em)]/(m)
•
v² = [(2).(3300000)]/(7500)
•
v² = (2).(440)
•
v² = 880
•
v = 29,66m/s
Nesse ponto a força centrípeta é para cima e também pode
ser calculada. Veja seu cálculo:
•
Fc = (mv²)/r
•
Fc = (7500).(880)/r
•
Fc = 6600000/r (não sabemos o raio da curva)
Outra coisa legal desse ponto é que nele nós tivemos sensação de
aumento de peso. Essa sensação varia durante todo o percurso e,
se o carrinho passar pela parte de cima da ‘lombada’, parece que
o peso diminui.
“
Katapul é uma
montanha-russa
de aço, localizada
no parque de
diversões Hopi
Hari. É a única
montanha-russa
de propulsão do
Brasil
”
Ciências da Natureza e Suas Tecnologias
LA TOUR EIFFEL
Esse simulador de elevador não é muito bom, afinal, ele faz as pessoas caírem em queda-livre por 47 metros. Os próximos
22 metros dessa torre de 69m são utilizados para a frenagem, realizado por intermédio de aparatos eletromagnéticos.
Após a queda-livre, o carrinho de massa 1000kg pode chegar ao máximo de 26,11m/s (94km/h). Os efeitos desse
brinquedo podem ser observados na foto à direita:
No topo da Tour Eiffel, a energia mecânica de cada carrinho é:
• Em = Ep + Ec • Em = Ep (o carrinho tá parado)
• Em = mgh • Em = (1000).(10).(69) (desconsideramos a massa das pessoas)
• Em = 690000J
Agora que sabemos a energia mecânica, podemos calcular a velocidade do
carrinho após a queda-livre:
• Em = Ep + Ec • 690000 = (1000).(10).(22) + (1000)(v²)/(2)
• 690 = 220 + v²/2 • 470 = v²/2
• v² = 940 • v = 30,65m/s
A velocidade calculada é diferente da velocidade real, porque desconsideramos
o atrito em nosso raciocínio, por conveniências de cálculo. Agora, podemos calcular
a aceleração dos freios magnéticos a partir da equação de Torricceli. Acompanhe-nos:
• V²fim = v² + 2as (v (minúsculo) é o mesmo do exemplo anterior) • 0 = 940 + (2).(a).(22)
• a = -(940/44) • a = -21,36m/s2
KATAPUL
Katapul é uma montanha-russa de aço, localizada no parque de diversões Hopi Hari.
É a única montanha-russa de propulsão do Brasil (em que o trem não necessita de subir
por meio de uma corrente para adquirir energia: ele já é lançado). Tem 220,1 metros de
extensão, atinge 85,3km/h em 3 segundos, e possui uma altura de 42 metros, fazendo
com que seja a montanha-russa de aço mais alta do Brasil. O trem é lançado da estação
por meio de um contrapeso de 40 toneladas que encontra-se dentro de uma torre branca
abaixo da primeira subida da atração. O contrapeso cai com uma certa velocidade, fazendo com
que um sistema de roldanas e cabos se movimentem, encaixando um aparelho chamado Pusher
atrás do último vagão, e este, por sua vez, empurra o trem até a velocidade de 85,3Km/h em apenas
3 segundos.
Ao atingir 85,3Km/h, o pusher solta o trem, fazendo com que ele passe em um
looping de aproximadamente 18 metros, e em seguida, suba uma rampa de 42 metros e
inclinação de 70º. Ao chegar próximo ao topo dessa rampa, o trem já está sem energia
potencial, o que faz com que ele pare, e comece a voltar de costas.
Ao descer esse trecho de costas, o trem passa novamente no looping, percorre a área de lançamento, e passa pela estação onde sua
velocidade é controlada pelos freios, e depois, sobe outra rampa de 70º de inclinação. Sua energia potencial acaba novamente, fazendo com
que ele volte (de frente) para estação, e seja parado completamente.
Todo esse processo (do lançamento à parada total) ocorre em cerca de 30 segundos.
10 m
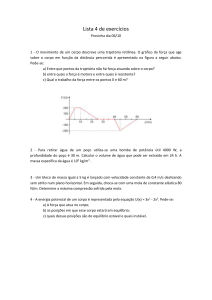
1. A figura abaixo apresenta um esquema simplificado de uma das maiores atrações do Parque Hopi Hari: o escorregador selvagem.
y
Nesse brinquedo, o visitante parte do ponto A com velocidade inicial nula e escorrega seguindo
A
P
uma das duas possíveis trajetórias –– I ou II –– indicadas na figura. A trajetória I corresponde
a um escorregador que liga os pontos A e B por meio de um segmento de reta. A trajetória II,
trajetória I
por sua vez, corresponde a um escorregador que liga os mesmos pontos A e B por meio de um
arco de circunferência, com centro no ponto P. Na figura ao lado, a trajetória indicada por III,
q
em linha tracejada, representa uma aproximação por dois segmentos de reta da trajetória II.
trajetória II
As trajetórias II e III têm em comum o ponto C, interseção entre o segmento de reta OP e o
trajetória III
arco de circunferência correspondente à trajetória II. No ambiente apresentado, considere que a
aceleração da gravidade seja igual a 10 m/s2.
Com base no texto, julgue os itens a seguir.
(1). Supondo a ausência de forças dissipativas, se duas pessoas partirem do ponto A
C
simultaneamente, uma pela trajetória I e a outra pela trajetória II, então elas chegarão ao ponto
B
B no mesmo instante.
x
O
10 m
(2). Supondo a ausência de atrito, quando duas pessoas de massas distintas m1 e m2 percorrerem as
trajetórias I e II, respectivamente, os trabalhos realizados pela força da gravidade em cada uma dessas pessoas serão iguais.
(3). Supondo a presença de força de atrito e que o módulo dessa força seja proporcional à força normal que atua em uma pessoa que está
escorregando, então, para a trajetória II, o módulo da força de atrito é uma função crescente de x.
(4). Suponha que uma pessoa de peso igual a 600N escorregue, a partir do ponto A, pela trajetória II e que o módulo da força de atrito que atua
sobre essa pessoa seja constante e igual a 240 2 N. Nessas condições, a energia cinética dessa pessoa no ponto B é menor que 1.200J.
(5). Supondo que dois visitantes V1 e V2 partam simultaneamente do ponto A pelas trajetórias I e II, respectivamente, então, ao chegarem
no ponto B, o módulo da velocidade do visitante V1 será maior que o da velocidade do visitante V2.
(6). Partindo do ponto A pela trajetória I, um visitante leva 2s para chegar ao ponto B.
(7). Partindo do ponto A, caso seguisse a trajetória III, um visitante levaria mais tempo para percorrer o trecho entre os pontos A e C que
para percorrer o trecho entre os pontos A e B, seguindo a trajetória I.
Quantos itens estão corretos?
a) cinco.
b) quatro.
c) três.
d)
dois. e)
um.
2.
Caminhando pelo Hopi Hari, encontra-se o barco viking. Esse brinquedo, ilustrado a seguir, quando em funcionamento, tem um movimento
análogo ao de um pêndulo simples. Quando o ponto A coincide com A’ ou B coincide com B', o barco atinge sua altura máxima. O barco
atingirá altura mínima quando os pontos P, P’e O estiverem alinhados.
2
FB NO ENEM
Ciências da Natureza e Suas Tecnologias
Considerando que a aceleração da gravidade seja igual a 10m/s2, que o sistema ao
lado seja simétrico com relação ao eixo OP e desprezando todas as forças dissipativas,
julgue os itens abaixo.
(1). Em relação ao ponto O, a energia potencial gravitacional do barco viking é máxima
quando A coincide com A’ ou B coincide com B’.
(2). Supondo que o centro de massa do barco coincida com seu centro geométrico, quando
o barco estiver em movimento, a sua energia cinética será máxima quando os pontos
P, P’ e O estiverem alinhados.
(3). O período de oscilação do barco depende de sua massa e não depende do comprimento
l das barras que o sustentam.
(4). Quando o barco estiver em movimento e os pontos P, P’ e O estiverem alinhados,
o módulo do vetor resultante da soma vetorial da tração em cada uma das barras
de sustentação será igual ao módulo do peso total do barco.
É(são) correto(s):
b) (1) e (3).
c) (1) e (2).
d) (2) e (4).
P´
A´
B´
O
e) (3) e (4).
3.
Um brinquedo muito procurado pelos visitantes do parque aquático água pura é o
toboágua irado, que consiste em um escorregador no qual o visitante parte do ponto A
com velocidade inicial nula e escorrega sobre uma boia por uma rampa reta, até o ponto B,
r
onde ele encontra uma piscina de água corrente, de velocidade constante v, permanecendo
na superfície da água sem afundar. Na
piscina,
o
visitante
é
levado
sobre
a boia pela
r
correnteza das águas com velocidade v, em linha reta, até o ponto C. As dimensões do
toboágua irado estão mostradas na figura ao lado, sendo o ângulo q ajustado de acordo
com a solicitação do visitante, para emoções mais fortes. O tempo total, em milissegundos
–– ms ––, que o visitante leva para percorrer o trajeto de A a C é dado pela fórmula: t(q) =
B
A
y
A
θ
10 m
a) todos os itens.
barras de sustentação
P
103 20 104
+
(1–tanq), em que g é a aceleração da gravidade, considerada igual
cos θ g
v
r
2
a 10m/s , v é o módulo de v e o ângulo q é dado em graus. Suponha que a densidade da
água seja de 1.000 kg/m3 e que a massa do sistema visitante-boia seja de 100kg.
Considerando o texto, julgue os itens que se seguem, e marque o incorreto
a) Na situação descrita, ao cair na água, parte da energia mecânica do sistema
atrito
visitante-boia é dissipada e transformada em outro tipo de energia.
b) Supondo que o sistema visitante-boia esteja descendo a rampa com
q = 30°, então todas as forças que atuam sobre esse sistema estão corretamente
ilustradas no diagrama ao lado.
c) Supondo as condições da hidrostática, para que o sistema visitante-boia flutue, é necessário
que parte dele seja composto de material com densidade menor que a da água.
d) Supondo as condições da hidrostática, para que o sistema visitante-boia flutue,
o seu volume imerso na água deve ser menor que 0,12m3.
e) O trabalho da força peso do sistema visitante-bóia é 104J.
10 m
B
(θ)
v
C
x
componente do peso
A
4.
imagem 1
imagem 2
imagem 3
Uma das atrações do Parque Beto Carrero é o conjunto de salas de espelhos, nas
quais o visitante pode ver sua imagem refletida de inúmeras formas divertidas: pequena,
grande, magra, gorda, distorcida etc. Em uma das salas disponíveis, dois espelhos planos
α = 90º
especiais A e B, de dimensões adequadas, são colocados formando um ângulo a entre eles.
B
O
O caso a = 90° é ilustrado na figura I à esquerda. Nesse caso, quando um objeto é colocado entre os
dois espelhos, duas imagens desse objeto são formadas nos espelhos A e B, como indicado nessa figura
imagem 3
pelas imagens 1 e 3. Uma outra imagem, indicada por 2, é gerada como resultado de múltiplas reflexões
girando-se o objeto inicial de um ângulo de 2a, no sentido anti-horário, em torno do ponto O.
Figura I
Para um ângulo a qualquer, uma lei de formação geral pode ser utilizada para
imagem 1
A
determinar todas as n imagens distintas obtidas. A figura II ilustra essa lei de formação,
para o caso a = 45°. As imagens indexadas por 1 e n, formadas nos espelhos A e B,
objeto inicial = respectivamente, são as imagens refletidas do objeto nesses espelhos. Outras imagens,
imagem 0
indexadas por k, para k=2, ..., n – 1, são geradas por múltiplas reflexões do objeto inicial
α = 45º
e de imagens desse objeto. Denominando-se o objeto inicial de imagem 0, para k=2, ...,
O
B
n – 1, a imagem k é obtida da imagem k –– 2 girando-se esta última de um ângulo de 2a, no
sentido
anti-horário, em torno do ponto O.
imagem 7
objeto inicial =
imagem 0
Com base nessas informações, julgue os itens a seguir.
Figura II
(1). No caso a = 45°, a figura
ilustra a imagem 5.
(2). No caso a = 22,5% desconsiderando-se o objeto inicial, o número de imagens distintas obtidas desse objeto é igual a 15.
(3). Para o caso em que são formadas exatamente n = 2m imagens distintas, para m ≥ 2, existem, contando-se a imagem 0,
exatamente 2m–1pares de imagens que são simétricas em relação ao ponto O, tais como as imagens 3 e 7, mostradas na figura II.
É(são) correto(s):
a) (1), (2) e (3) b) (2) e (3)
c) (1) e (3)
d) (2) e (3)
e) (1) e (2)
FB NO ENEM
3
Ciências da Natureza e Suas Tecnologias
5.
Continuando na sala dos espelhos do Parque Beto Carrero, encontramos o caleidoscópio. Leia o texto abaixo e responda ao
questionamento.
O físico alemão David Brewster é o inventor do caleidoscópio (1816). Inicialmente elaborado como uma ferramenta científica, o
caleidoscópio é vendido como um brinquedo muito popular, tanto para adultos como para crianças. O nome vem da união das palavras
gregas kalos (belo), eidos (imagem) e scopéo (vejo), ou seja, caleidoscópio quer dizer algo como "vejo belas imagens", o que de fato
acontece graças à simetria. Simetria é uma característica que pode ser observada na matemática, na biologia, na literatura, na física, nas
artes em geral e em diversos outros ramos do conhecimento.
O caleidoscópio é constituído, basicamente, por três espelhos planos retangulares que formam a superfície lateral de um prisma
triangular reto. Em todo espelho plano, um objeto e a sua imagem são simétricos em relação ao plano do espelho.
Observe a seção transversal de um caleidoscópio e algumas de suas infinitas imagens:
Entre as imagens numeradas da figura acima, qual está desenhada de modo incorreto?
a) I
b) II
c) III
d) IV
e) V
GABARITO (V.12)
1
B
2
E
3
D
4
D
5
A
Professor-Colaborador: Régis Nogueira
4
FB NO ENEM
OSG: 32874/10 - A.J/- REV.:Diego