UMA PROPOSTA DE ATIVIDADE PARA SALA DE AULA: O USO DE UM
APLICATIVO PARA AUXILIAR OS ALUNOS NOS ESTUDOS DE FUNÇÕES DO
PRIMEIRO GRAU
Prof. Me. Francinario Oliveira de Araújo
[email protected]
Resumo: Neste artigo iremos apresentar um aplicativo de matemática para que o professor
e/ou aluno possa usar na sala aula, ou em casa pelos alunos. Trata-se de um aplicativo
simples, ele pode ser executado em qualquer computador ou notebook que tiver o Java. Esse
aplicativo pode ser usado no cálculo da raiz, na determinação do sinal de uma função linear,
ou seja, mostrar onde a função é positiva e onde ela é negativa, o aplicativo também diz se a
função é crescente ou decrescente. A idéia é que esse aplicativo possa ser usado pelos alunos e
professores para verificação do resultado encontrado pelos alunos estão ou não corretos.
Palavras chave: aplicativo, função linear e ferramenta de ensino.
1. INTRODUÇÃO
É do conhecimento de todos, quer seja docente ou não, a respeito das dificuldades
enfrentadas por alunos e professores durante o processo de ensino e aprendizagem dos
conceitos de matemática. Grande parte dos alunos do ensino básico (ensino fundamental e
médio) usa a desculpa de que matemática é difícil, e que apenas pessoas inteligentes são
capazes de aprender.
Esse problema é cultural, desde sempre, os alunos ouvem de familiares e amigos o
quanto matemática é complicada e sem aplicabilidade no seu dia-dia, e para completar, ainda
existem professores de matemática que usam o método tradicional de ensino.
O fato de muitos professores seguirem a metodologia apenas com aulas expositivas,
onde o objetivo central é tentar cumprir ao máximo a ementa. Como se apenas a transmissão
dos conteúdos de um livro texto fosse suficiente. Atualmente, apenas o que importa para os
alunos do ensino médio se resume em quais conteúdos serão cobrados na prova do ENEM
(Exame Nacional do Ensino Médio), e muitas vezes os alunos não conseguem levar para sua
vida os conhecimentos adquiridos no ensino básico.
Minha experiência em sala de aula como professor de matemática da rede básica de
ensino foi apenas durante os estágios obrigatórios durante o curso de graduação. Mas, ainda
assim com o pouco contato com esse público, percebi o quão difícil é para os docentes
conseguir ministrar suas aulas e conseguir atingir o objetivo desejado, que é ver o
desenvolvimento dos alunos.
Sempre me questionei, o que os docentes podem fazer para tornar as aulas de
matemática mais dinâmica e atrativa? Questionamento difícil de ser respondido, dessa forma,
cabe ao professor identificar a realidade de cada turma e assim tentar escolher a metodologia
mais adequada para a mesma.
Diante dessa realidade, podemos citar algumas metodologias que os professores
podem usar em suas aulas, como por exemplo: uso de jogos e/ou meterias concretos,
modelagem matemática, fazer uso da história da matemática no ensino de matemática,
etnomatemática, recursos computacionais e tecnológicos no ensino, entre outros.
Notamos que a tecnologia faz parte de vários setores do nosso cotidiano. Então fica a
pergunta, como podemos trazer essa tecnologia para o âmbito educacional, em particular para
o processo de ensino e aprendizagem de matemática? O professor deve refletir bastante antes
de inserir essa nova ferramenta em sala de aula.
Basta apenas o professor mencionar que irá fazer uso do computador em sua sala de
aula, que certamente os alunos ficaram curiosos para saber qual relação deve existir entre
matemática e computador, uma vez que a maior parte dos alunos não vê aplicação da
matemática. O computador por si só já prende a atenção dos alunos, o mesmo ainda pode
oferecer experiências que seriam bem difíceis de conseguir com o uso apenas de papel e lápis.
Segundo Freire e Prado (2000) é imprescindível que o professor busque fazer a coesão
entre sua prática pedagógica e os meios tecnológicos, sendo assim, devemos pensar em
reconstruir o referencial norteador de uma prática, e deixar de encarar a informática como um
recurso, mas pensar nela como uma forma de (re)pensar a educação como um processo
investigativo do aluno na construção do seu conhecimento.
Nesse trabalho apresentaremos um aplicativo para computador (que em breve poderá
ser usado em celulares também) que pode ser usado pelos alunos e/ou professores, como
ferramenta para ser usado durante a resolução de exercícios de função linear. O aplicativo é
bem fácil de ser manipulado, pois necessita apenas de entrar com dois números e clicar na
opção desejada, veremos mais detalhes a seguir.
2. METODOLOGIA
De acordo com os (PCN’s,1998), a formação do aluno deve ter como objetivo central a
aquisição dos conhecimentos básicos e o desenvolvimento de capacidades tais como: de
pesquisar, buscar informações, selecioná-las e analisá-las; a capacidade de formular hipóteses,
verificá-las e testá-las. Desta forma, é preciso que o educador procure aspectos considerando
positivos no software a ser utilizado em suas aulas, visando sempre ampliar aspectos de
inteligência (Valente, 1991, p. 16-31).
Sabemos que existem várias ferramentas computacionais, que podem sem usadas como
facilitador no processo de ensino e aprendizagem encontrados na web, são softwares
educacionais voltados para o ensino de matemática. Esses softwares podem ser pagos ou não.
Iremos listar agora alguns softwares que podem ser usados como ferramenta no processo
de ensino e aprendizagem de matemática. Essa lista foi tirada de LENZ, FERRAZ (2007) ver
quadro 1, para maiores informações a respeito desses softwares sugerimos a leitura de LENZ
e FERRAZ (2007), lá os autores fazer um breve resumo a respeito de cada software.
Área da matemática
Na área da geometria
Gráficos
Softwares
1. Cabri Géomètre
2. Sketchpad
3. Cinderella
4. Dr Geo
5. Geoplan
6. Geospace
7. Régua e Compasso
8. Geometria Descritiva
9. Euklid
10. Wingeom,
11. S-Logo
12. Poly
13. Shapari
1.
2.
3.
4.
5.
6.
7.
8.
Graphmatica
Modellus
Winplot
MathGV
Ratos
Vrum-Vrum
Graphequation
CurveExpert;
Álgebra
1. Winmat
Cálculos em planilhas
1. Microsoft Execel
Recreativos
1.
2.
3.
4.
5.
6.
Tangram
Torre de Hanói
OOG (Object Orientation Game)
Winarc
Polytris
Tess
Quadro 1- Exemplos de softwares que podem ser usados nas aulas de matemática
Fonte(LENZ, FERRAZ, 2007, P. 11)
Com base no que foi exposto acima, notamos que existem várias possibilidades para o
uso de softwares no ensino de matemática. Porém, nosso trabalho tem como proposta, o uso
de um aplicativo para trabalhar função linear (até o presente momento o aplicativo pode ser
executado em qualquer computador que tenha o JAVA, e em um futuro próximo estaremos
executando em outros dispositivos). O aplicativo desenvolvido para este trabalho é bem
simples de ser operado, podemos usá-lo para trabalhar função linear, mais especificamente os
seguintes aspectos: calcular a raiz, calcular o sinal da função, determinar se a função é
crescente ou não. O aplicativo ainda não desenha o gráfico da função linear, mas já estamos
resolvendo esse detalhe.
Sabemos que para o uso dos softwares o usuário tem que saber os comandos do
mesmo. Por exemplo, para resolver um sistema linear no Scilab, podemos escrever o sistema
na forma matricial Ax = b, e depois usar o comando linsolve. Isso foi apenas um exemplo, e
isso faz com que os professores percam o interesse pelo uso dessa ferramenta, pois muitas
vezes o professor não tem tempo suficiente para elaborar uma aula com o uso de software.
O conjunto de ferramentas necessárias para desenvolver, compilar e executar
aplicativos Java precisa de um kit conhecido como Java Development Kit (JDK). Podemos
baixar
esse
kit
no
site
(http://www.oracle.com/technetwork/java/javase/downloads/index.html) o download é
gratuito e fácil.
Depois de instalado o JDK compatível com seu computador, para iniciar a
programação em Java é necessario um editor de texto para editar os programas. Existem
muitos Ambientes de Desenvolvimento – Integrated Development Environment (IDE), que
dão suporte a linguagem Java. Um IDE é um programa de computador que reune ferramentas
de apoio ao desenvolvimento de software com o objetivo principal de agilizar o processo de
codificação. Há vários IDEs para programação Java, podemos citar o NetBeans e o Eclipse.
Nesse artigo usaremos o NetBeans IDE 8.1 ver a figura 1 que mostra a interface do
NetBeans IDE 8.1. Esse IDE é um ambiente de desenvolvimento com muitas vantagens,
como por exemplo: é gratuito, de código aberto, além de ser executado em muitas
plataformas, como Windows, Linux, Solaris e MacOS, sendo fácil de instalar e usar.
O NetBeans IDE 8.1 é uma excelente ferramenta para criar interface grafica, pois é
muito prático e fácil. Em resumo, podemos montar uma interface gráfica apenas clicando e
arrastando os butões e acessórios desejados.
Figura1: Interface gráfica do NetBeans IDE 8.1
A figura 2 mostra a interface gráfica do nosso aplicativo, podemos trabalhar alguns
conceitos de função linear, nesse aplicativo o usuário (professor e/ou aluno) poderá trabalhar
os seguintes conceitos de função linear:
1. Calcular a raiz de uma função linear, ou seja, encontrar o valor de x tal que f(x)=0.
2. Calcular o sinal da função linear, isto é, saber para quais valores de x a função linear é
positiva, e para quais valores de x a função linear é negativa.
3. Calcular o comportamento da função linear, ou seja, o aplicativo mostra se a função
linear é crescente ou decrescente.
Figura2 - Interface do aplicativo
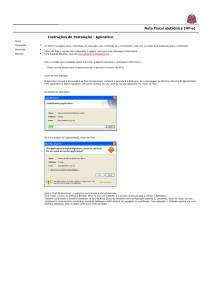
3. FUNCIONAMENTO DO APLICATIVO
O usuário (professor e/ou aluno) deve entrar com os valores a e b, onde a tem que ser
diferente de zero, e essas constantes compõem a função linear f(x)=ax+b. Agora iremos
descrever a função de cada botão do aplicativo.
Botão do aplicativo
Função do botão
Esse campo de texto é para o usuário entrar com o
valor do coeficiente angular da função linear, ou
seja, o termo a.
Esse campo de texto é para o usuário entrar com o
valor do coeficiente independente da função
linear, ou seja, o termo b.
Esse botão vai verificar se o termo digitado no
primeiro campo de texto é diferente de zero. Caso
o valor seja diferente de zero então os botões
calcular a raiz, calcular o sinal, crescente ou
decrescente é liberado para o usuário. Caso o valor
seja zero vai aparecer a seguinte mensagem para o
usuário ver a figura 3.
Figura3
Esse botão calcula a raiz da função linear
escolhida pelo usuário.
Esse botão calcula o sinal da função linear
escolhida pelo usuário, ou seja, ao clicar nesse
botão o aplicativo vai mostrar onde a função linear
é positiva e onde ela é negativa.
Esse botão calcula o comportamento da função
linear escolhida pelo usuário, ou seja, ao clicar
nesse botão o aplicativo vai mostrar se a função
linear é crescente ou decrescente.
Quando o usuário clicar nesse botão o aplicativo
vai limpar os dados dos dois campos de textos de
entrada de dados. Além disso, os botões calcular a
raiz, calcular o sinal, crescente ou decrescente
serão desativados.
Ao clicar nesse botão o aplicativo será fechado.
Quadro 1-Descrição dos botões do aplicativo
Agora daremos um exemplo de uma aplicação do aplicativo, para isso, tomemos a
seguinte função linear f(x)=2x-10, de onde tiramos os seguintes dados a=2 e b=-10. Com
base nesses dados, já sabemos que:
1. A raiz é 5;
2. A função linear e positiva para x>5 e negativa para x<5;
3. Como o valor de a>0, então a função linear é crescente.
Para maiores detalhes ver a figura 4.
Figura4: exemplo de uma aplicação do nosso aplicativo
4. CONSIDERAÇÕES FINAIS
A proposta central desse trabalho era, apresentar um aplicativo que pudesse ser usado
como ferramenta, no processo de ensino e aprendizagem de função linear. O aplicativo ainda
está em fase de construção, essa é a primeira versão do aplicativo, essa versão pode ser
executada apenas em computador, a única exigência é que o computador tenha o Java. Ainda
temos as seguintes melhorias a fazer nesse aplicativo:
1. Fazer com que o aplicativo construa o gráfico da função linear;
2. Fazer com que o aplicativo seja executado em outros dispositivos como, por exemplo,
aparelho celular.
O ponto positivo dessa versão desse aplicativo é a facilidade com que ele pode ser
utilizado. Ele não requer nenhum comando especifico para seu uso. Para manipular esse
aplicativo, o usuário digita os valores a e b, correspondentes aos da função linear f(x)=ax+b e
clicar no botão verificar, caso o valor a seja não nulo, os demais botões serão liberados, e em
seguida o usuário clica no botão com a função desejada, e ver o resultado. Pontos negativos
são: o fato de não desenhar o gráficos ainda; e ser executado apenas em computadores. Mas,
esses dois pontos negativos serão solucionados em breve.
Essa ferramenta vem para ajudar no processo de ensino e aprendizagem de função
linear. O aplicativo vai ajudar os alunos na hora dos exercícios, pois muitas vezes o aluno não
tem certeza se sua resposta está correta ou não, já que muitos livros não têm as respostas dos
exercícios, e nesse sentido o aplicativo vai ajudar bastante.
5. REFERÊNCIAS
VALENTE, J. A. (Org.) (1998). Computadores e conhecimento: repensando a educação. 2.
ed. Campinas: UNICAMP/Núcleo de Informática Aplicada à Educação (NIED), 1998.
VALENTE, J.A. (1991). Uso do Computador na Educação. In: Liberando a Mente:
Computadores na Educação Especial, (pp. 16-31). Campinas, Gráfica Central da
UNICAMP.
JUNIOR, A. C. (2002). Novas Tecnologias Educacionais no Ensino de Matemática:
Estudo de Caso - Logo e do Cabri-Géomètre, UNIVERSIDADE FEDERAL DE SANTA
CATARINA – UFSC, Programa de Pós-graduação em Engenharia de Produção, Dissertação
de Mestrado, Florianópolis, SC.
LENZ, E.A.; FERRAZ, I. R. (2007). Ferramentas de informática: Usando recursos da
informática para o ensino e aprendizagem de matemática, (pp. 11). Universidade
Paranaense - UNIPAR.
LEVY, P. As tecnologias da inteligência: o futuro do pensamento na era da informática.
Rio de Janeiro: Editora 34, 1995.
BRASIL. Ministério da Educação, Secretaria de Educação Média e Tecnológica. Parâmetros
curriculares nacionais: ensino médio. Brasília. MEC. 1999; BRASIL. Ministério da
Educação, Secretaria de Educação Média e Tecnológica. PCN+- ensino médio, orientações
educacionais complementares aos parâmetros curriculares nacionais. Brasília. 2002.
Disponível em: <http://www.sbfisica.org.br/ensino/pcn.shtml>. Acesso em: 10-06-2016.
VALENTE, J. A. Informática na educação: conformar ou contornar a escola.
Perspectiva. Universidade Federal de Santa Catarina, Florianópolis, n. 24, 1995.
FREIRE, F. M. P.; PRADO, M. E. B. O computador em sala de aula: articulando saberes.
Campinas, SP: UNICAMP/NIED, 2000.