Ruído em amplificadores

Instrumentação e Técnicas de Medidas
Ruído Elétrico e Componentes Reais
Controle de Versões
2013
Versão 1 – Instrumentação e Técnicas de Medidas (ITM)
Com base nas notas de aula de COB783 e Op Amp Applications Handbook,
Section 4, edited by Walt Jung (Newnes, 2006).
Última alteração: 11/10/2013
Índice
20 Ruído elétrico em circuitos com amplificador operacional............................................................4
20.1 Ruído Térmico........................................................................................................................4
20.2 Shot Noise...............................................................................................................................4
20.3 Ruído de Contato....................................................................................................................5
20.4 Popcorn Noise.........................................................................................................................5
20.5 Soma de Ruídos......................................................................................................................6
20.6 Espectro de ruído....................................................................................................................7
20.7 Equivalente Elétrico................................................................................................................8
20.8 Razão sinal ruído....................................................................................................................9
20.9 Figura de ruído........................................................................................................................9
20.10 Exemplo: Ruído..................................................................................................................10
20.10.1 Tabela de erros............................................................................................................11
21 Componentes Passivos (Resistores Capacitores).........................................................................13
21.1 Resistores e potenciômetros..................................................................................................13
21.1.1 Efeitos térmicos.............................................................................................................13
21.1.2 Elementos parasitas.......................................................................................................14
21.1.3 Falhas, variação com o tempo e ruído...........................................................................15
21.1.4 Potenciômetros..............................................................................................................15
21.2 Indutores...............................................................................................................................16
21.3 Capacitores............................................................................................................................16
21.3.1 Absorção Dielétrica.......................................................................................................17
21.3.2 Elementos parasitas (Rp, ESR e ESL)..........................................................................18
21.3.3 Tolerância......................................................................................................................20
20 Ruído elétrico em circuitos com amplificador operacional
Ruído elétrico é todo o tipo de interferência que se sobrepõe a uma informação elétrica. Para
evitar confusão, a partir deste momento, a palavra “sinal” passa a representar a informação útil ao
passo que a palavra “ruído” será utilizada para referenciar qualquer tipo de interferência elétrica
sobre um determinado sinal. O ruído elétrico nos operacionais se deve ao ruído inerente a cada
dispositivos que o compõe (transistores, resistores, etc....).
Existem várias formas de ruído elétrico sendo que cada uma destas formas está associada a
algum evento físico ou a alguma característica de confecção do componente. A seguir, são listados
os principais tipos de ruído, suas fontes e seus efeitos na saída dos AO. A Texas Instruments tem
dois bons textos sobre o assunto, o Op Amp Noise Theory and Applications e o Noise Analysis In
Operational Amplifier Circuits.
20.1 Ruído Térmico
Este ruído é causado pela agitação térmica dos elétrons em uma resistência. O ruído térmico
é constante ao longo de todo o espectro de frequências, e por isso é chamado de “ruído branco”. A
tensão eficaz gerada pelo ruído térmico pode ser calculada com a equação 20.1.
V T  RMS = 4 kTBR [ V ] ( 20.1 )
onde: k é a constante de Boltzman (1,38⋅10-23J/K); T é a temperatura [K]; B é a banda
passante [Hz]; R é a resistência [Ω].
No osciloscópio o ruído térmico aparece como o desenho da Figura 20.1.
Figura 20.1: Aparência do ruído térmico.
.
20.2 Shot Noise
Este ruído está associado com uma corrente fluindo através de uma barreira de potencial.
Isto significa que ele é formado pela flutuação instantânea de corrente elétrica, causada pela
emissão aleatória de elétrons e lacunas. Schottky, em 1918, mostrou que este ruído gera uma
corrente eficaz, que pode ser quantizada de acordo com equação 20.2.
I SN  RMS = 2 qI DC B [ A ]
( 20.2 )
onde: q é a carga do elétron (1,6⋅10-19C); IDC é a corrente média [A]; B é a banda passante
[Hz].
Quanto ao espectro de frequências o shot noise é similar ao ruído térmico, pois a densidade
de potência é constante com a frequência.
20.3 Ruído de Contato
Também conhecido por Excess Noise, Flicker Noise, ruído 1/f e ruído de baixa frequência, é
causado pela variação da condutividade devido ao contato imperfeito entre dois materiais (por
exemplo, silício e alumínio). Este tipo de ruído aparece sempre que existe junções entre materiais
de qualquer tipo, como nas chaves, pontos de solda etc.. A equação 20.3 mostra a intensidade da
corrente pela qual pode ser modelado este ruído.
I f RMS =
KI DC  B
[ A ] ( 20.3 )
f
onde: K é uma constante que depende do material; IDC é a corrente média [A]; B é banda
passante [Hz]; F é a frequência [Hz].
Note que o ruído de contato If aumenta com a diminuição da frequência. Esta é a maior fonte
de ruído em componentes à baixas frequências. Para dois resistores de 1kΩ , um de carbono e outro
de fio, o ruído térmico é o mesmo e proporcional a resistência. Porém, com a passagem de corrente
elétrica o resistor de carbono apresenta mais ruído que o resistor de fio devido a variação de
condutividade no contato imperfeito do resistor.
20.4 Popcorn Noise
Este ruído é responsável pelo conhecido “estalo” que aparece, por exemplo, em aparelhos de
som. É causado por defeitos de manufatura da junção (tal como uma impureza) de componentes
semicondutores. Este tipo de ruído depende do processo de fabricação dos semicondutores. O
popcorn tem a aparência de um degrau de tensão de duração aproximada de 10 ms e que aparece
esporadicamente nos aparelhos. A Figura 20.2 mostra a aparência destes ruídos quando visto em
osciloscópio. Este tipo de ruído está praticamente extinto dos amplificadores operacionais modernos
uma vez que o grau de pureza dos materiais utilizados é elevado.
Figura 20.2: Aparência do ruído popcorn
20.5 Soma de Ruídos
Várias são as fontes de ruído e todas podem estar presentes ao mesmo tempo em um mesmo
circuito. Quando isto ocorre e os ruídos não são correlacionados, ou seja, são independentes. O
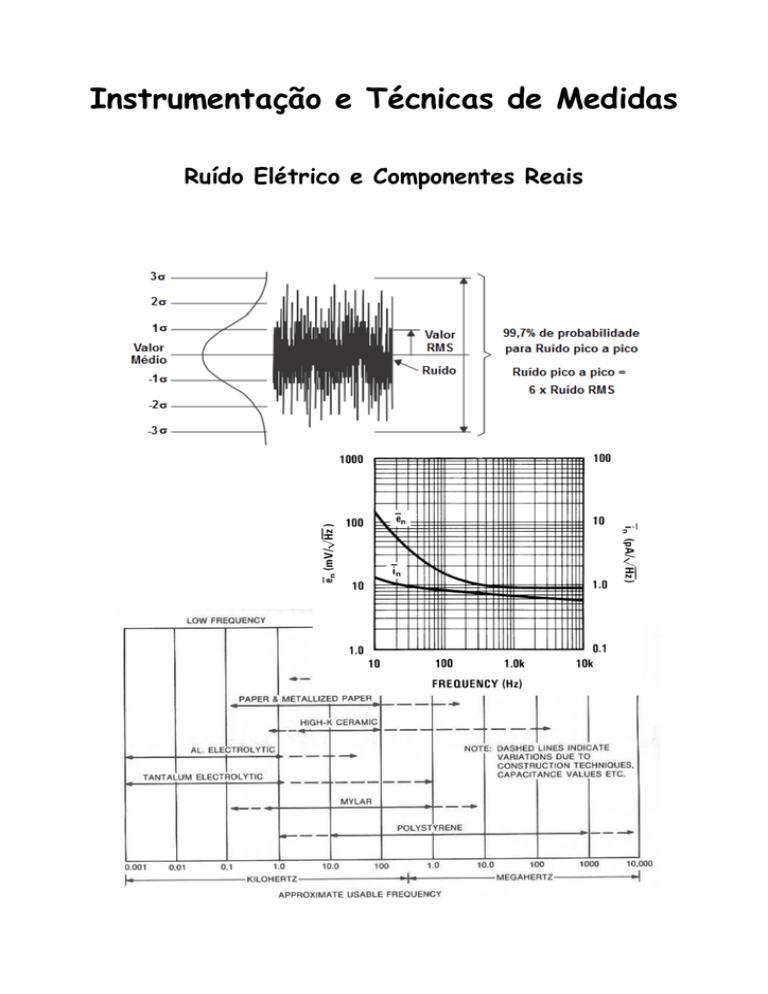
ruído RMS total é como se fosse o desvio padrão de uma distribuição de probabilidade normal com
média zero (Figura 20.3). Por esta razão a soma das fontes de ruído produz uma potência total que é
igual a soma da potência de cada fonte, de acordo com a equação 20.4. O resultado também pode
ser expresso em termos de uma fonte de tensão como na equação 20.5.
Figura 20.3: Relação entre ruído de pico a pico e RMS.
P T =P1 P 2...P n

2
2
( 20.4 )
2
V T = V 1 V 2 . . .. .V n
( 20.5 )
Algumas vezes, entretanto, o ruido é expresso em termos de valores pico a pico. Nestes
casos, é comum dividir o valor pico a pico por 6 para se obter uma informação RMS de corrente ou
tensão (Figura 20.3).
20.6 Espectro de ruído
Um gráfico de ruído equivalente é construído com auxílio de filtros passa faixa sintonizados
ou de processamento digital de sinais. A representação do ruído sempre é feita no domínio da
frequência.
A curva de tensão e corrente de ruído para um AO típico é mostrada na Figura 20.4. Note as
unidades nV /  Hz e pA/  Hz para cada frequência específica. Se desejarmos conhecer o ruído
para uma faixa de frequências basta integrar este ruído na faixa de frequência desejada. Observe
também que há um ruído 1/f preponderante para as baixas frequências mas que fica praticamente
constante a partir da chamada frequência de “corte”. Quando a faixa de interesse não inclui a
frequência de corte ou é três décadas maior que ela o efeito deste ruído de baixa frequência pode ser
desprezado. Quando esta faixa for importante a integral pode ser calculada como
√
V N (RMS )=V Nplano⋅ f NC⋅ln
( )
f Máx
+( f Máx − f Min ) [V]
f Min
onde fMáx e fMin são as frequências máximas e mínimas da faixa de interesse, VNplano a tensão
de ruído na faixa plana, e fNC a frequência de corte do ruído 1/f. Se fNC não for dada ou não puder ser
obtida pelo gráfico ela pode ser calculada como
f
NC
(V
=
2
N
)
( f )∣f = fx – V Nplano ⋅ fx
2
V
2
Nplano
[Hz]
onde VN(f) é a tensão de ruído na região 1/f para uma frequência fx.
Figura 20.4: Corrente e tensão de ruído para um AO típico (National, AN 104, May 1974).
Por exemplo, para a Figura 20.4, na banda de 10Hz até 10kHz:
2
f
NC
≈
2
[(110nV / √ Hz) −(9,5 nV / √ Hz) ]⋅10
2
(9,5 nV / √ Hz )
√
V N (RMS )=9,5 nV / √ Hz⋅ 1330⋅ln
(
=1330Hz
)
10000
+(10000−10)=1,315μ V
10
Como os filtros destas bandas de frequência não são ideais, é necessário aplicar uma
correção aos valores calculados. Para filtros de primeira ordem é necessário multiplicar o resultado
por 1,57. Para filtros de segunda, terceira e quarta ordem os multiplicadores são 1,11, 1,05 e 1,025
respectivamente.
20.7 Equivalente Elétrico
Fontes de tensão e corrente podem ser aplicadas para modelar a influência do ruído em um
AO. Conforme apresentado na Figura 20.5 estas fontes são aplicadas da mesma forma que para
modelar VOS e IB.
Figura 20.5: Modelo do AO com fontes de ruído.
20.8 Razão sinal ruído
Para avaliação de amplificadores também se utiliza a chamada razão sinal ruído (SNR),
definida conforme equação 20.6. Quanto maior a razão SNR melhor o amplificador.
SNR=20⋅log

Vsinal RMS
Vruído RMS

( 20.6 )
20.9 Figura de ruído
A figura de ruído corresponde a razão entre as SNR na entrada do amplificador (como se ele
não existisse) e na sua saída. Note que para esta medida é importante que os valores da impedância
da fonte de entrada (o gerador de sinais) sejam consideradas.
NF =10⋅log

SNRin
SNRout

NF =10⋅log

Sinal in⋅Ruído out
Sinal out⋅Ruídoin

NF =10⋅log

2
Sinal in⋅Av⋅V TNin

Sinal in⋅Av⋅V 2T
,
onde Av é o ganho de tensão do amplificador, V TNin é a tensão de ruído total na entrada do
amplificador, VT é a tensão de ruído térmico na resistência da fonte.
 
2
NF =10⋅log
V TNin
2
VT
NF =10⋅log

V 2nV 2T  I 2n⋅R 2gerador
V 2T

Supondo que o único ruído do gerador seja o ruído térmico, quando conectarmos este
gerador ao amplificador a tensão de ruído se soma a tensão do gerador e a corrente de ruído,
passando pela resistência do gerador produz outra tensão de ruído que depende da impedância de
entrada do gerador. Por esta razão, para pequenos valores de impedância do gerador a tensão de
ruído tem importância maior que a corrente. Se a resistência do gerador é grande a corrente de ruído
é mais importante. Uma clara vantagem do amplificador com entrada FET, pois assim como as
correntes de polarização a corrente de ruído destes amplificadores é muito menor que nos TBJ.
20.10 Exemplo: Ruído
Para o amplificador cuja tensão e corrente de ruído são apresentadas na Figura 20.4,
supondo que ele está conectado a um gerador com impedância de 2kΩ (National Semiconductor,
Application Note 104, May 1974).
a) Calcular o ruído equivalente total na entrada do amplificador operando a 1kHz (por
unidade de frequência).
No resistor da fonte (para 1Hz de banda): V T = 4⋅k⋅T⋅R⋅B=5,7 nV /  Hz
Da Figura 20.4 vem que
V n |1kHz =9,5 nV /  Hz
I n |1kHz =0,68 pA/  Hz
Total: V TN =  V 2nV T2  I 2n⋅R 2gerador =11,16 nV /  Hz
b) Calcular o ruído equivalente total na entrada do amplificador operando entre 1kHz e
10kHz.
V TN =11,16 nV /  Hz⋅ 10kHz – 1kHz=1,1  V RMS
Observe que para banda larga (sinais acima de 10kHz, por exemplo), pode se considerar
constante mesmo o ruído de baixa frequência (abaixo de 100Hz, neste exemplo), uma vez que o
erro será pequeno.
c) Calcular a relação sinal ruído na entrada do amplificador, supondo que o sinal do gerador
possui apenas 4mVRMS.
SNR=20⋅log


V gerador
=71dB
V TN
20.10.1 Tabela de erros
Como a análise realizada neste capítulo sempre trata de tensões e correntes muito pequenas
nem sempre é fácil ter uma noção clara da ordem de grandeza dos erros que estão sendo discutidos.
Em sistemas digitais, a resolução de equipamentos é sempre mais facilmente compreendida pois a
medida é quantizada em um número finito de possibilidades. Nesta secção será calculado o erro
total em um sistema de aquisição de sinais com medida em ponte e o resultado será comparado com
a resolução equivalente de um AD, de forma que fique mais simples de se entender as preocupações
apresentadas anteriormente. O problema original está em In-Amp Bridge Circuit Error Budget
Analysis.
Suponha o caso de uma ponte com todos os elementos variando conectada a um
amplificador de instrumentação AD620B que deve ser interligado a um sistema de aquisição de
dados. Qual a resolução necessária para o AD de forma a obtermos uma saída estável?
Neste exemplo consideraremos que a impedância equivalente da ponte é de 350Ω com saída
máxima de 100mV e excitação de 10V. O ganho do amplificador de instrumentação foi programado
para ser de 100 vezes (para produzir um sinal de saída de 10V). As especificações do AD620 para
25oC são Vos=55µV, Ios=0,5nA, Erro de Ganho = 0,15%, Não linearidade de 40ppm, ruído de 0,1
até 10Hz de 280nVpp e CMR=120dB @ 60Hz. A tabela a seguir consolida os erros para esta
medida:
Parâmetro
Cálculo
Contribuição
Compensar
Vos
55µV / 100mV
550ppm
sim
Ios
(350Ω ⋅ 0,5nA) / 100mV
1,8ppm
sim
Erro de ganho
0,15%
1500ppm
sim
Erro de CMR
120dB: (1ppm ⋅ 5V) / 100mV 50ppm
sim
Ruído (0,1 até 10Hz)
280nV / 100mV
2,8ppm
não
Erro de linearidade
40ppm
40ppm
não
Erro total (pior caso)
≈ 9 bits exatidão
2145ppm (tudo)
Erro total (melhor caso) ≈ 14 bits exatidão
42ppm (linearidade+ruído)
Observa-se que foi calculado o erro de CMR para o sinal de modo comum em CC (obtido na
ponte alimentada com 10V). Este erro resulta em um offset na saída do amplificador. Não foi
calculado quanto pode resultar de ruído de 60Hz devido ao CMR do amplificador. Observa-se
também que todos os erros de offset ou ganho podem ser compensados mas os erros relativos a
ruído e não linearidade do amplificador não. Assim, para o pior caso teríamos que usar um AD de 9
bits e para o melhor caso um AD de 14 bits.
21 Componentes Passivos
Neste capítulo são apresentadas as características reais de resistores, capacitores e indutores
e como eles podem influenciar no desempenho de circuitos.
21.1 Resistores e potenciômetros
Resistores e potenciômetros podem ser feitos, entre outros, de compósitos de carbono,
filmes de carbono, metal, filme metálico e fios (indutivos e não indutivos). Um bom texto sobre
resistores, falando sobre suas características e parâmetros pode ser obtido na Vishay – Resistors
101, How to select resistors e How to select resistors for precision applications. O texto apresentado
aqui tem como base principalmente os exemplos e descrições contidas em Hardware and
Housekeeping Techniques. São apresentados os problemas mais comuns envolvendo o uso de
resistores e potenciômetros em aplicações de precisão.
21.1.1 Efeitos térmicos
Resistores reais são sensíveis a variação de temperatura o que pode alterar ganhos e
aumentar a propagação de erros. Os efeitos destas variações podem ser facilmente percebidos com o
uso de exemplos simples. Por exemplo, supondo um amplificador não inversor de ganho
G=1+
R1
R2
onde R1=9,9kΩ, ¼ W e TC=25ppm/°C e R2=100Ω, ¼ W e TC=50ppm/°C, uma variação de 10°C
leva a erros de 250ppm/°C (dez vezes a diferença entre os TC). Observe que isto é equivalente a 1
LSB em um conversor de 12 bits. O uso de resistores com TC iguais não significa que este
problema está resolvido uma vez que alguns resistores, como os de compósito de carbono, podem
ter coeficientes térmicos bem elevados com TC=1500ppm/°C ou mais. Nestes casos qualquer
pequena diferença nos TC pode ser significativa e mesmo uma variação de 1% nestes TC resulta em
uma diferença de 15ppm/°C.
O autoaquecimento também pode ser um problema. Para o mesmo ganho do exemplo
anterior, considerando que os dois TC=25ppm/°C, quando a saída chega a 10V a dissipação em R1
é de 9,9mW e a de R2 é de 0,1mW. Se a resistência térmica destes resistores é de 125°C/W, então
R1 aquece 1,24°C e R2 aquece 0,0125°C. Isto resulta em uma diferença de 31ppm no ganho, o que
pode levar a um erro de ½ LSB num AD de 14 bits. Este autoaquecimento pode causar efeitos de
não linearidades ainda piores se o ganho for elevado. Neste caso o melhor a fazer é dividir o ganho
em mais de um estágio e usar resistores com resistência térmica menor (resistores de maior
potência).
Para o caso de resistores de pequeno valor (<10Ω) o vilão pode ser a resistência de trilhas,
fios e interconexões, que passam a ter valor não desprezível. Ademais, o TC do cobre, por exemplo,
é de aproximadamente 3900ppm/°C, e mesmo que o resistor utilizado tenha TC baixo, o TC do
cobre adicionando resistência ao circuito faz com que o TC equivalente seja muito maior do que o
do resistor.
Para piorar ainda mais as coisas o TC dos resistores e o próprio valor das resistências pode
mudar após vários ciclos de calor e frio. O valor dos resistores também pode mudar com a tensão
aplicada por razões completamente diferentes do autoaquecimento.
21.1.2 Elementos parasitas
Resistores apresentam capacitâncias e indutâncias parasitas que costumam ser pronunciadas
em altas frequências. Estes elementos parasitas são expressos em termos de erro percentual para a
diferença entre a impedância e a resistência CA com relação a resistência CC. Neste aspecto um dos
piores casos é o dos resistores de fio. Mesmo para os casos ditos não indutivos pode ser encontrada
indutância de 20µH para valores menores que 10kΩ e 5pF para resistores com mais de 10kΩ. Estas
características levam ao surgimento de picos, oscilações e aumento no tempo de estabilização para
respostas ao degrau, ou seja, alterações dinâmicas associadas a resposta em frequência.
Para altas frequências (acima de 0,1GHz) o modelo da próxima figura pode ser utilizado
para resistores de filmes finos. Os componentes R, L e C representam o resistor enquanto que LG e
CG representam as interconexões.
Efeitos termoelétricos também podem ser importantes. Diferentes ligas de cobre podem
gerar entre 1µV/°C e 20µV/°C para resistores de filme metálico comuns, ou 400µV/°C para
resistores de carbono. Mesmo assim isto não costuma ser um problema muito grande pois as tensões
de cada terminal tendem a se cancelar se a distribuição de calor for simétrica. Isto, entretanto, nem
sempre acontece e vai depender da forma e local onde os componentes estão conectados. Por
exemplo, componentes deitados sobre a placa tendem a apresentar a mesma temperatura em ambos
os terminais mas isto pode não ser verdadeiro caso os resistores sejam colocadas na vertical como
na próxima figura.
21.1.3 Falhas, variação com o tempo e ruído
Resistores podem queimar e abrir (filme de carbono) ou queimar e curto-circuitar (filme
metálico). Os resistores podem mudar com o tempo (ppm/ano) sendo necessário realizar ciclos de
aquecimento até a estabilização (resistores de metal filme precisa de 4 a 5000 horas para
estabilizar). O ruido gerado pelos resistores não necessariamente é o mesmo uma vez que alguns
resistores também apresentam ruído 1/f. Os resistores menos ruidosos são os de filme de carbono,
metal filme e fios.
21.1.4 Potenciômetros
Quanto ao uso de potenciômetros e trim-pots estes podem se danificar com poeira,
solventes, umidade e uso além de adicionarem ruído de contato ao circuito. De um modo geral o
uso destes componentes deve ser evitado ou minimizado e seu uso pode ser substituído por
potenciômetros digitais ou arranjos com conversores DA. Estas soluções evitam os problemas
mecânicos e permitem o ajuste automático dos componentes em circuitos realimentados. Quando
for usar um potenciômetro lembre-se “use com infinito cuidado e ajuste em faixa infinitesimal para
evitar infinita frustração.
21.2 Indutores
Indutores não são componentes comuns em circuitos eletrônicos nem em instrumentação
pois, na prática, estão longe de se comportar como seu modelo ideal e não são fáceis de fabricar
com dimensões reduzidas e estáveis (de um modo geral só são comercializadas indutâncias estáveis
e pequenas com valores de alguns nH até alguns µH). Mesmo assim os indutores são componentes
importantes em fontes de alimentação, filtros (incluindo filtro contra EMI), bobinas choke,
casamento de impedância e osciladores. Para caracterizar bem os indutores atuais, pontuando as
diferentes tecnologias e nomenclaturas empregadas, dois textos da Vishay pode ser utilizados. O
primeiro é o Inductors 101, e o segundo é o Inductor and Magnetic Product Terminology.
Para se obter indutâncias maiores em um espaço menor é comum o uso de núcleos
magnéticos de ferro, ferrite, cerâmicas, mumetal, permalloy entre outros, porém estes materiais
podem saturam, tornando o indutor num elemento não linear. Adicionalmente a temperatura
também apresenta efeitos sobre os núcleos alterando as suas propriedades.
As espiras dos indutores se comportam como placas condutoras paralelas, conferindo ao
indutor características capacitivas. Como consequência o indutor real pode oscilar e apresenta como
um dos parâmetros de manual uma frequência de ressonância. Completando o cenário, os fios que
formam o indutor apresentam resistência não nula, nem sempre desprezível, e que, por efeito skin,
pode variar com a frequência. Indutores nunca terão impedância (paralela) elevada (MΩ) pois a
resistência da bobina e a capacitância parasita vão limitar estes valores. Desta forma o Q dos
indutores nunca é muito alto e vai limitar o Q de circuitos sintonizados a valores em torno de 100,
enquanto ressonadores cerâmicos podem chegar a 1.000 e cristais a 10.000 ou mais. Esta limitação
na seletividade, entretanto, não é necessariamente ruim. Núcleos e braçadeiras de ferrite (ferrite
beads) usados para filtros, por exemplo, apresentam baixo Q e por isso podem atuar eliminando
interferências em uma ampla banda de frequências.
21.3 Capacitores
Capacitores reais são produzidos com os mais variados dielétricos e, por isso, apresentam
características distintas tanto no que diz respeito ao valor da capacitância, a faixa de frequência em
que podem ser utilizados, a tensão de funcionamento e outros. Assim, capacitores reais estão longe
do ideal. A figura abaixo apresenta um modelo equivalente para eles, e tabelas comparativas podem
ser obtidas nas páginas dos fabricantes como a AVX e a HolyStone. Na figura C é o capacitor, Rp
modela as perdas, ESR é a resistência de terminais e placas, ERL modela a indutância de terminais
e placas, RDA-CDA modela a absorção dielétrica (DA).
21.3.1 Absorção Dielétrica
A absorção dielétrica está associada a polarização do dielétrico. Capacitores que ficam
muito tempo carregados “polarizam” o dielétrico. Isto causa uma espécie de histerese ou efeito
memória no capacitor. Considerando que o modelo apresentado está correto e que o capacitor é
carregado, parte da carga é armazenada em C e parte em CDA. Mesmo depois de curto-circuitar os
terminais do capacitor e esperar que a tensão em seus terminais caia a zero não é possível garantir
que a tensão sobre CDA será nula (há uma constante de tempo associada a esta descarga). Isto
significa que, ao abrir os terminais do capacitor, uma tensão residual pode aparecer em seus
terminais. O efeito pode ser visualizado na figura a seguir.
Este problema pode ser importante em integradores e comparadores além de ser responsável
pelo surgimento de offset ou não linearidades em conversores V-F. Também podem resultar em
erros na tensão armazenada em S&H quando há troca de canais com tensões muito diferentes,
filtros e sistemas de controle (elevada constante de tempo – vários ms ou mais). A solução para este
problema passa pelo uso de capacitores de boa qualidade (evite usar capacitores cujo fabricante não
informa a DA) ou sistemas realimentados com autozero.
Material
DA
Teflon, poliestireno, polipropileno
0,02%
Cerâmica
0,2% - 0,6%
Mica, vidro
5%
Eletrolítico, tântalo
10%
OBS.: Observe que um erro de 0,2% representa um erro de ½ LSB em conversores AD de 8 bits.
21.3.2 Elementos parasitas (Rp, ESR e ESL)
Todos os elementos parasitas dos capacitores são informados pelos fabricantes. As perdas
que são modeladas pela resistência Rp costumam ser informadas pelo nome IR (insulation
resistance). Normalmente esta resistência é dependente da tensão de alimentação e pode ser
informada tanto como um valor de resistência quanto como uma contante de tempo (produto Rp⋅C).
Estes valores podem variar de 1s para capacitores eletrolíticos até milhões de segundos para
capacitores de teflon, poliestireno e polipropileno. Isto significa que mesmo desconectado o
capacitor carregado pode descarregar em poucos segundos ou vários dias. A tabela a seguir mostra
valores comuns para diferentes tipos de capacitores.
Material
Constante de Tempo
Eletrolítico
1s
Cerâmica
100s
Vidro
1.000s
Teflon e poliestireno e polipropileno
1.000.000s
A indutância e a resistência de terminais e placas (ESL e RSL), por outro lado, afetam
diretamente o comportamento da resposta em frequência do capacitor. Assim, capacitores com
diferentes dielétricos e processos de fabricação serão recomendados para diferentes faixas de
frequência. Na próxima figura observa-se o comportamento de dois capacitores produzidos por
processos diferentes. Observe que para baixas frequências o capacitor se comporta como tal, para
altas frequências o capacitor se comporta como um indutor e para uma frequência intermediaria
apresenta ressonância série com impedância limitada ao valor de RSL.
É este comportamento que restringe o uso de capacitores para frequências elevadas. De um
modo geral capacitores eletrolíticos, de tântalo ou construídos com placas e dielétricos enrolados
apresentam ESL elevada limitação maior de frequência. Por está razão é comum ver circuitos onde
um pequeno capacitor é colocado em paralelo com grandes capacitores eletrolíticos ou de tântalo.
Este pequeno capacitor tem função apenas para frequências elevadas, evitando que o circuito
apresente característica marcadamente indutiva. A próxima figura apresenta as faixas de uso para
cada tipo de capacitor.
Todos estes elementos parasitas (ESR, ESL e Rp) são apresentados de forma conjunto por
meio de um parâmetro conhecido como fator de dissipação (DF). O DF é definido pela razão entre
resistências e reatâncias, ou seja, é um parâmetro que mede a ineficiência do capacitor relacionando
a relação entre a energia perdida e energia armazenada. Como uma aproximação Q≈1/DF.
21.3.3 Tolerância
Adicionalmente a obtenção de capacitores de precisão não é fácil. Sob demanda é possível
encontrar capacitores com tolerância de 0,5 ou 1% (cerâmica NP0, alguns filmes finos) mas valores
comuns estão entre 5 e 10%. A temperatura e a frequência também influenciam a capacitância, a DF
e a DA. Coeficientes térmicos da ordem de 30ppm/ oC (cerâmica NP0) e 100 a 200ppm/ oC
(poliestireno e polipropileno) são comuns. A faixa de operação também varia muito. Alguns
capacitores de filmes finos funcionam até 85oC enquanto que os de teflon funcionam até 200oC.