formatação final M1-parte1

ATENÇÃO:
O material a seguir é parte de uma das aulas da apostila
de MÓDULO 1 que por sua vez, faz parte do CURSO
de ELETROELETRÔNICA ANALÓGICA -DIGITAL
que vai do MÓDULO 1 ao 4.
A partir da amostra da aula, terá uma idéia de onde o
treinamento de eletroeletrônica poderá lhe levar.
Você poderá adquirir o arquivo digital da apostila
completa (16 aulas), ou ainda na forma impressa que
será enviada por por correio. Entre na nova loja
virtual CTA Eletrônica e veja como:
www.lojacta.com.br
Além de ter a apostila e estuda-la, torne-se aluno e
assim poderá tirar dúvidas de cada uma das questões
dos blocos atrelados a cada uma das aulas da apostila,
receber as respostas por e-mail, fazer parte do
ranking de módulos e após a conclusão do módulo
com prova final, participar do ranking geral e poder
ser chamado por empresas do ramo de eletroeletrônica.
Saiba mais como se tornar um aluno acessando nossa
página de cursos:
www.ctaeletronica.com.br/web/curso.asp
APOSTILA ELÉTRICA PARA ELETRÔNICA
LEI DE OHM - POTÊNCIA - RESISTORES VARIÁVEIS
AULA
8
A lei de Ohm e suas diversas interpretações
A potência elétrica e o efeito Joule
Potância de 10 e a nomenclatura de Grandezas
Resistores variáveis e ajustáveis:
Potenciômetros - Trimpots
LEI DE OHM
Como já tínhamos comentado no capítulo anterior,
no século XIX, o cientista Georg Simon Ohm,
enunciou uma lei da física
que envolve Resistência,
Corrente e Tensão. Ele
chegou a estas
conclusões através de
muitos experimentos
práticos, e conseguiu
uma “equação” que pode
relacionar a queda de
tensão sobre uma
resistência com a
Georg Simon Ohm
corrente que passa por
ela. Essa “lei” é empírica
e na época em que foi enunciada não podia ser
comprovada matematicamente por nenhum
cálculo, só podia ser comprovada na prática. Só
muitos anos depois essa “lei” pode ser comprovada
teoricamente pela física e por cálculos diferencias
complexos.
Essa “lei” básica, é fundamental nos processos
envolvendo as grandezas chamadas TENSÃO,
CORRENTE e RESISTÊNCIA, ou seja, se
V
(a)
V=
V
RI
Desta mesma “lei” podemos derivar estas outras
expressões:
I = V/R
e
R=V/I
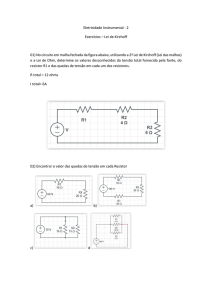
Na figura abaixo, mostramos a manifestação da
lógica da lei de ohm, através de uma série de
medições de tensão e corrente em um circuito
formado por uma bateria, lâmpada e um resistor.
Como a lâmpada possui uma tensão de trabalha de
aproximadamente 3V (no circuito está funcionando
com 3,4V), será necessário existir um resistor em
série com a lâmpada que terá maior valor que esta
(pouco mais do dobro), e nele haverá a queda do
restante da tensão da fonte. Para medirmos a
Lp
i
+
I
R
(b)
aplicarmos 1 volt sobre uma resistência de 1 ohm,
haverá a circulação de corrente de 1 ampère.
Na LEI DE OHM a corrente é diretamente
proporcional a tensão aplicada (quando uma
aumenta a outra também aumenta) e inversamente
proporcional a resistência (quando uma aumenta a
outra diminui).
A LEI DE OHM é expressa na seguinte fórmula:
V=RxI
ELETRÔNICA
MÓDULO - 1
corrente que circula pelo circuito, deveremos
colocar a ponta vermelha do multímetro, no polo
positivo da bateria e com a ponta preta do, fechar a
ligação do circuito, obrigando a corrente da malha a
circular não somente pelo circuito, mas também
pelo multímetro, permitindo a medição da corrente
total da malha.
ELETRICIDADE - ATOMOS - TENSÃO - CORRENTE - RESISTÊNCIA - CORRENTE ALTERNADA E CONTÍNUA - FORMAS DE ONDA - CAPACITORES - ANÁLISE DE DEFEITOS SÉRIE-PARALELO - POTÊNCIA - LEI DE OHM
75
APOSTILA ELÉTRICA PARA ELETRÔNICA
Trabalhando agora com um circuito semelhante ao
anterior, vamos fazer diversas considerações.
Fica claro que se ligarmos uma lâmpada cuja
resistência seja de 6 ohms em uma bateria de 12V,
circulará uma corrente de 2A (figura 1). O raciocínio
é simples, pois se aplicássemos uma tensão de 12V
sobre uma resistência de 12 ohms, haveria uma
corrente circulante de 1A; como a resistência
equivale à metade da tensão, maior corrente irá
circular, e será o dobro.
figura 1
Lp1 = 6W
12V
I1= 2A
Caso a resistência seja maior do que a especificada
acima, a corrente resultante será menor, tantas
vezes quanto for a relação entre a resistência e a
tensão.
Como exemplo, podemos dizer que uma resistência
de 120 ohms será dez vezes maior que a
comparação com a tensão de 12V, gerando uma
corrente dez vezes menor que o padrão (No caso de
12 volts sobre 12 ohms = 1 ampère) que será de
0,1A, como mostra a figura 2. Neste exemplo,
podemos ver que a corrente circulante é 10 vezes
menor, portanto o brilho da lâmpada (Lp2) deve
também ser menor.
figura 2
Lp2 = 120W
12V
I2 = 0,1A
Já para uma lâmpada com resistência de 1,2 ohm, a
corrente será dez vezes maior, ou seja, 10A, como
vemos na figura 3, e neste caso, o brilho da lâmpada
(Lp3) será maior que no 1° caso, cuja resultante de
corrente era de 2A (figura 1).
figura 3
Lp3 = 1,2
12V
I3 = 10A
Agora, podemos pegar outro exemplo com uma
lâmpada de resistência de 1.200 ohms, como
mostra a figura 4.
Para calcularmos a corrente circulante na lâmpada
podemos utilizar a fórmula da lei de Ohm para
cálculo de corrente: I = V / R , então substituindo os
76
MÓDULO - 1
valores de V e R teremos I = 12V / 1200 ohms =
0,01A.
Podemos perceber pela figura 4, que a lâmpada
está apagada, o que é compatível com a corrente
calculada, pois temos uma corrente circulante de
apenas 0,01 A, o que não é suficiente para
“incandescer” o filamento e “criar” luminosidade.
Portanto, apesar de circular corrente pela lâmpada,
ela permanece apagada.
POTÊNCIA ELÉTRICA
Outra grandeza elétrica muito importante é a
POTÊNCIA. Essa grandeza não é exclusiva da
eletricidade, pois abrange várias áreas do nosso dia
a dia.
A definição de Potência é a quantidade de
energia (Trabalho) dissipada (ou absorvida) por
intervalo de tempo. Agora, aplicando essa
definição para a eletrônica teremos, em primeiro
lugar que definir a energia elétrica de um
componente eletrônico?
A corrente elétrica é a quantidade de cargas
elétricas que se movem por segundo ( I = Q/s), e a
tensão elétrica é o potencial elétrico. Como o
potencial elétrico (campo elétrico) multiplicado pela
carga elétrica gera a energia elétrica, temos então
uma relação para Energia, Tensão e Corrente, e
portanto teremos V x I = V x Q / s = En / s = Potência.
Resumindo estas relações podemos definir
Potência Elétrica (P) :
P=Vx I
A unidade da potência é o watt, simbolizado pela
letra “W” (letra maiúscula).
As lâmpadas em geral, apresentam duas
especificações que são a tensão de trabalho e a
potência que as mesmas fornecem. Isto quer dizer
que, se quisermos saber qual será a corrente de
uma lâmpada de 6W por uma tensão de trabalho de
12V:
P=VxI
6W = 12V x I
I = 6W / 12V = 0,5A
Pela expressão acima conseguimos calcular a
corrente circulante por uma lâmpada de 6 watts
ELETRICIDADE - ATOMOS - TENSÃO - CORRENTE - RESISTÊNCIA - CORRENTE ALTERNADA E CONTÍNUA - FORMAS DE ONDA - CAPACITORES - ANÁLISE DE DEFEITOS SÉRIE-PARALELO - POTÊNCIA - LEI DE OHM
ELETRÔNICA
APOSTILA ELÉTRICA PARA ELETRÔNICA
ligada a uma fonte de 12 volts, que é de 0,5 ampère.
Muitas vezes, será necessário colocarmos
resistências em série com a carga para não só
limitarmos a corrente, como também gerar uma
menor queda de tensão sobre a carga.
Como exemplo, podemos citar uma bateria que
possui uma tensão de 12V e nela queremos ligar
uma lâmpada de 6V por 6W, como mostramos na
figura 5.
MÓDULO - 1
figura 6
2
IxR
V2
R
IxV
P
V
V
R
P I
V R
PxR
P
2
I
2
IxR
Fica fácil definir por dedução, que se o valor da
tensão é igual a potência, resulta em uma corrente
de 1A, ou seja, para o acendimento correto dessa
lâmpada deveria circular uma corrente de 1A.
Como a tensão da fonte é o dobro da tensão de
trabalho da lâmpada, devemos colocar uma
resistência que limite a passagem da corrente, que
por coincidência deverá receber a mesma tensão
aplicada à lâmpada (6V).
Como estamos aplicando 6V sobre a lâmpada e
pela mesma circula 1A, usando a lei de Ohm, já
sabemos de antemão que sua resistência é de 6
ohms (pela proporção aplicada). Portanto o valor do
resistor a ser utilizado em série com a lâmpada
deverá ser também de 6 ohms.
O problema agora será calcular a potência
dissipada por este resistor, que também não é difícil,
pois já sabemos que a tensão sobre o mesmo será
de 6V e a corrente de 1A, ou seja, 6 watts. Como
segurança, o resistor deverá ter uma potência de
30% a mais do que o especificado para o trabalho.
V
P
V
I
EFEITO JOULE
O efeito Joule nada mais é do que o efeito de
aquecimento provocado em um resistor ou
resistência, quando submetido a uma tensão que
gera por ela uma corrente circulante, esta corrente
circulante provocará o aquecimento do resistor (ou
resistência). Ao aquecer o resistor começa a
dissipar calor para o meio (ar, água ou o material no
qual está preso o resistor). Então, podemos dizer
que a energia elétrica que o resistor recebe está se
transformando em calor (energia térmica ou
cinética).
EXERCÍCIOS
1) No circuito abaixo (figura 7), calcule a corrente
circulante e a potência dissipada pela lâmpada Lp1
e pelo resistor R1:
Um resumo da LEI DE OHM (inclusive
com o cálculo de potência) pode ser
visto na figura 6.
RESUMO DA LEI DE OHM
2) No circuito abaixo (figura 8), calcule o valor de R2,
a queda de tensão sobre R2 e a potência dissipada
pela lâmpada Lp2 e pelo resistor R2:
8
As relações de potência, tensão, corrente,
resistência estão todas descritas no diagrama da
figura 6. Notem que utilizando apenas uma frase
que diz” Quem Vê... RI” ou “quem V = R . I”
consegue-se ter a fórmula inicial para obter as
outras:
Exemplos : V = R x I e P = V x I
ELETRÔNICA
R2 = 24W
Lp2
POTÊNCIA DE 10
A potência de 10 é utilizada para simplificar a
“escrita” de números muito grandes ou muito
pequenos. Ela utiliza algumas regras para
uniformidade das representações dos números;
ELETRICIDADE - ATOMOS - TENSÃO - CORRENTE - RESISTÊNCIA - CORRENTE ALTERNADA E CONTÍNUA - FORMAS DE ONDA - CAPACITORES - ANÁLISE DE DEFEITOS SÉRIE-PARALELO - POTÊNCIA - LEI DE OHM
77
APOSTILA ELÉTRICA PARA ELETRÔNICA
baseia-se no fato que o número da potência de 10 é
simplesmente igual ao número de “zeros”. Exemplo
3
10 = 1000 (3 “zeros”).
Os números expressos em potência de 10 e que
obedeçam as regras de apresentação numérica em
potência de 10 é chamado de NOTAÇÃO
CIENTÍFICA.
A notação científica, é o modo conveniente de
utilizar-se na solução de problemas que envolve
grandezas físicas (eletricidade, mecânica,
astronomia, etc.)
Em notação científica, o coeficiente da potência de
10 é sempre expresso em um número maior ou igual
a “1” e menor que “10”, e obedece as seguintes
regras:
MÓDULO - 1
Regra n° 4 - Para converter um número expresso
com uma potência de 10 positiva em um número
decimal, desloca-se a casa decimal para a direita,
tantas casas ou posições quanto o valor do
expoente.
Ex:
6,15 x 106 = 6.150.000 (o expoente é 6,
deslocando-se a vírgula 6 casas para a direita).
Regra n° 5 - Para multiplicar dois ou mais números
expressos como potência de 10, multiplica-se os
coeficientes e somam-se os expoentes para se
obter o novo expoente de 10.
7
Ex: 3x10-3 x 5x10 = (3x5) x (10(-3 + 7))= 15x10
Regra n° 1 - Para escrever números maiores que
“1” na forma de um número pequeno, utilizamos
potência de “10”, ou seja, desloca-se a casa decimal
para a esquerda tantos algarismos quanto o
desejado, e a seguir multiplica-se o n° obtido por 10,
elevado a uma potência igual ao número de casas
deslocadas.
Ex: 3.000 = 3,0 x 1000 = 3x103 (a vírgula é
deslocada 3 casas para a esquerda, sendo o
expoente 3).
150,32 = 1,5032 x 100 = 1,5032x102
Regra n° 2 - Para escrever números menores do
que 1, como um número inteiro, multiplicado por
uma potência de 10, desloca-se a casa decimal
para a direita, tantos algarismos quantos forem
necessários. A seguir multiplica-se o n° obtido por
10 elevado a uma potência NEGATIVA igual ao
número de casas decimais deslocadas.
4
Agora, vamos pegar o valor de 15x104 e passar
para notação científica, pegando o coeficiente “15”
e passando para um número menor que “10” e
5
maior que “1” ficando com 1,5 x 10 .
Regra n° 6 - Para dividir uma potência de 10, utilizase a fórmula:
1 / 10n = 10-n
Podemos assim mover qualquer potência de 10 do
numerador para o denominador ou vice e versa,
simplesmente mudando o sinal expoente.
Ex: 15 / 2x10-1 = 15/2 x 101 = 7,5 x 10
Frequentemente, exprimimos uma resposta
utilizando-se um prefixo em vez de utilizar uma
notação científica.
Os prefixos métricos são os seguintes:
Ex: 0,006 = 6,0 x 0,001 = 6x10-3 (a vírgula é
deslocada para a direita 3 casas, a potência ou
expoente é de -3).
TERA (T) = 1012 = 1.000.000.000.000
GIGA (G) = 109 =
1.000.000.000
6
MEGA (M) = 10 =
1.000.000
3
KILO
(k)
=
10
=
1.000
Regra n° 3 - Para converter um número expresso
-3
mili
(m)
=
10
=
0,001
com uma potência negativa de 10, em um número
-6
decimal, desloca-se a vírgula para a esquerda micro (m) = 10 = 0,000.001
-9
tantas casas quanto o valor do expoente.
nano (n) = 10 = 0,000.000.001
pico (p) = 10-12 = 0,000.000.000.001
-9
Ex: 7,14 x 10 = 0,00000000714
78
ELETRICIDADE - ATOMOS - TENSÃO - CORRENTE - RESISTÊNCIA - CORRENTE ALTERNADA E CONTÍNUA - FORMAS DE ONDA - CAPACITORES - ANÁLISE DE DEFEITOS SÉRIE-PARALELO - POTÊNCIA - LEI DE OHM
ELETRÔNICA
APOSTILA ELÉTRICA PARA ELETRÔNICA
MÓDULO - 1
RESISTORES AJUSTÁVEIS E
VARIÁVEIS
potenciômetro linear
potenciômetro linear deslizante
e os extremos, com sua resistência variando
linearmente de acordo com a rotação de seu cursor.
O potenciômetro linear é dominante na grande
maioria das aplicações de potenciômetros.
Na figura 10, mostramos a esquerda, a tabela de
variação de valor ôhmico por graus de rotação, e a
direita o cursor do potenciômetro e suas posições
relativas em graus.
figura 10
R ( W)
100
Em algumas aplicações necessitamos alterar a
resistência de determinado circuito para obter uma
condição precisa. Temos assim os resistores
ajustáveis que estão dentro do equipamento e são
C
A
A
C de ajuste semi-fixo ou de
B
B
fábrica, ou seja, após
A B C
ajustados, dificilmente
precisarão ser mexidos. A
figura 9b, mostra a forma
A B C
física desses componentes
e seu aspecto simbólico.
POTENCIÔMETRO
TRIMPOT
Os resistores ajustáveis
também são chamados de TRIMPOT.
Já os potenciômetros são
chamados de variáveis pois
são constantemente
alterados de valor permitindo
ao usuário ajustar várias
funções. Os potenciômetros
de volume, brilho, contraste,
etc. são resistores variáveis
(1) terminais de ligação
muito conhecidos do público
(2) terminal central
(3) pista de carvão
em geral (figura 9a). Apesar
(4) conjunto ligado ao eixo
de serem muito úteis eles
móvel
(5) haste que liga o terminal estão sendo substituídos por
central à pista
comandos do microproces(6) eixo
sador (inclusive os resistores
ajustáveis internos).
POTENCIÔMETROS
O valor do potenciômetro é dado a partir de sua
resistência máxima (de extremo a extremo) sendo
que o cursor ou parte móvel, poderá ser
posicionada tendo ela uma resistência em relação a
um dos extremos e outra resistência em relação ao
outro extremo.
75
160
80o
50
240o
25
0
o
ELETRÔNICA
320
o
Limites máximos
de rotação
o
80
o
160
o
240
o
320
POTENCIÔMETRO LOGARÍTMICO
O potenciômetro logarítmico é aquele que resulta em
uma variação exponencial
de sua resistência em
relação ao ângulo de
rotação de seu eixo. Essa
variação foi muito usada
para controle de volume de
diversos equipamentos, já
que o ouvido humano tem
uma percepção logarítmica.
Ve j a n a f i g u r a 11 o
Em alguns aparelhos mais
levantamento gráfico da antigos, o potenciômetro de
variação de resistência em volume, cujo valor era logaríera acoplado à chave
função da rotação do eixo; o timico,
liga/desliga do aparelho.
resultado será uma curva
exponencial.
figura 12
R (W )
100
160
45
80
o
o
240
o
22
0
POTENCIÔMETRO LINEAR
O potenciômetro linear é aquele que apresenta uma
variação uniforme de sua resistência entre o cursor
o
o
320
o
10
o
80
o
160
240
o
o
320
ELETRICIDADE - ATOMOS - TENSÃO - CORRENTE - RESISTÊNCIA - CORRENTE ALTERNADA E CONTÍNUA - FORMAS DE ONDA - CAPACITORES - ANÁLISE DE DEFEITOS SÉRIE-PARALELO - POTÊNCIA - LEI DE OHM
79
APOSTILA ELÉTRICA PARA ELETRÔNICA
MÓDULO - 1
Na figura 12 mostramos vários tipos de resistores ajustáveis e variáveis.
potenciômetros
trimpots
COMO INTERPRETAR O POTENCIÔMETRO
COMO DOIS RESISTORES
A
A
A
Exercícios: coloque as tensões
corretas nos circuitos
A
1k
1k
C
2k
C
2k
1k
1k
B
A
B
Com o cursor em aberto ele
valerá entre A e C a metade
do valor total e entre C e B
mais metade do valor total.
A
B
B
B
Neste caso o cursor está
todo para baixo, indicando
que entre os pontos A e B o
potenciômetro valerá o teu
valor total
A
A
1k
A
1k
2k
C
2k
E
1k
1k
D
B
B
Neste caso a parte de baixo
do potenciômetro foi
eliminada pelo cursor,
passando a valer só a parte
de cima (A à B = 1k ohms)
B
F
B
Neste caso toda a extensão
do potenciômetro foi
eliminada, sendo a
resistência entre A e B de 0
ohms (curto)
A = 4,5V; B = 4V C = 5V D = 5V E = 3,75V F = 7,5V
Para maiores informações sobre as matérias da 8a. aula, indicamos para o aluno adquirir os volumes de Análise de
Defeitos (12 volumes), comprando um a um. Além disso, pedimos para acessar os links abaixo:
Lei de Ohm
trimpot
potenciômetros
tipos de potenciômetros
80
http://br.geocities.com/saladefisica3/laboratorio/ohm/ohm.htm
http://www.eletronika.net/wp/lei-de-ohm
http://pt.wikipedia.org/wiki/Trimpot
http://pt.tech-faq.com/potentiometer.shtml&prev=hp&rurl=translate.google.com
http://www.arsolcomp.com.br/potenciometro
ELETRICIDADE - ATOMOS - TENSÃO - CORRENTE - RESISTÊNCIA - CORRENTE ALTERNADA E CONTÍNUA - FORMAS DE ONDA - CAPACITORES - ANÁLISE DE DEFEITOS SÉRIE-PARALELO - POTÊNCIA - LEI DE OHM
ELETRÔNICA