Física - Etapa

Questão 11
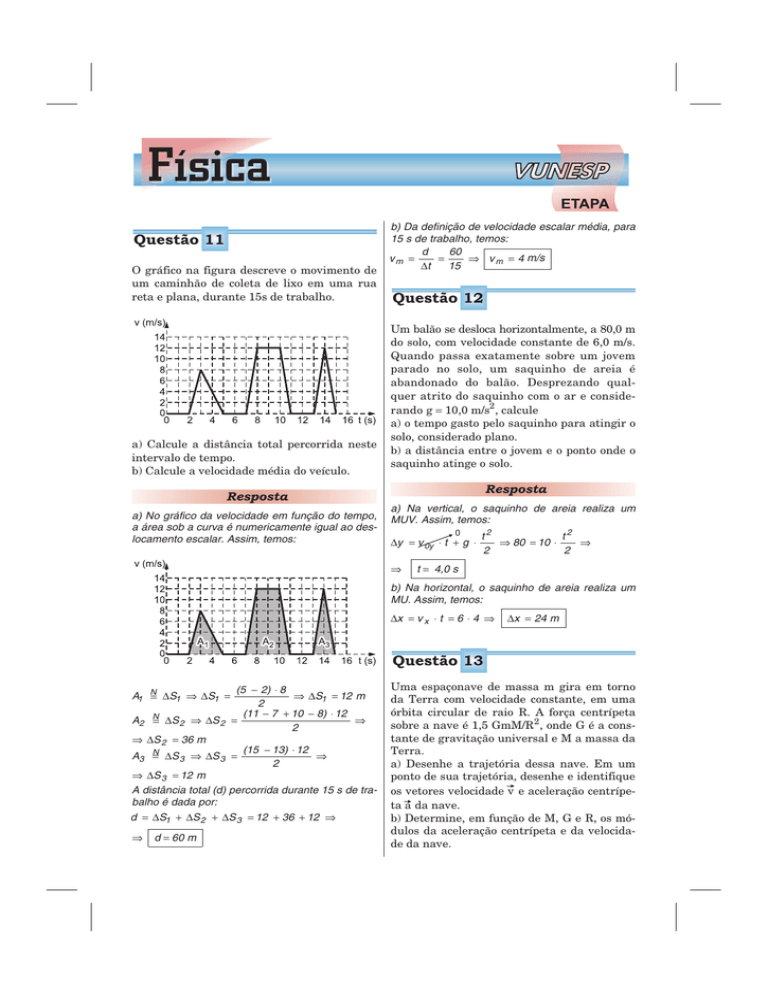
O gráfico na figura descreve o movimento de
um caminhão de coleta de lixo em uma rua
reta e plana, durante 15s de trabalho.
a) Calcule a distância total percorrida neste
intervalo de tempo.
b) Calcule a velocidade média do veículo.
Resposta
a) No gráfico da velocidade em função do tempo,
a área sob a curva é numericamente igual ao deslocamento escalar. Assim, temos:
b) Da definição de velocidade escalar média, para
15 s de trabalho, temos:
60
d
vm =
=
⇒ v m = 4 m/s
15
∆t
Questão 12
Um balão se desloca horizontalmente, a 80,0 m
do solo, com velocidade constante de 6,0 m/s.
Quando passa exatamente sobre um jovem
parado no solo, um saquinho de areia é
abandonado do balão. Desprezando qualquer atrito do saquinho com o ar e considerando g = 10,0 m/s2 , calcule
a) o tempo gasto pelo saquinho para atingir o
solo, considerado plano.
b) a distância entre o jovem e o ponto onde o
saquinho atinge o solo.
Resposta
a) Na vertical, o saquinho de areia realiza um
MUV. Assim, temos:
0
∆y = v 0y ⋅ t + g ⋅
⇒
t2
t2
⇒ 80 = 10 ⋅
⇒
2
2
t = 4,0 s
b) Na horizontal, o saquinho de areia realiza um
MU. Assim, temos:
∆x = v x ⋅ t = 6 ⋅ 4 ⇒
∆x = 24 m
Questão 13
A1 N
= ∆S1 ⇒ ∆S1 =
A2 N
= ∆S 2 ⇒ ∆S 2
(5 − 2) ⋅ 8
⇒ ∆S1 = 12 m
2
(11 − 7 + 10 − 8) ⋅ 12
=
⇒
2
⇒ ∆S 2 = 36 m
N
A3 =
∆S 3 ⇒ ∆S 3 =
(15 − 13) ⋅ 12
⇒
2
⇒ ∆S 3 = 12 m
A distância total (d) percorrida durante 15 s de trabalho é dada por:
d = ∆S1 + ∆S 2 + ∆S 3 = 12 + 36 + 12 ⇒
⇒
d = 60 m
Uma espaçonave de massa m gira em torno
da Terra com velocidade constante, em uma
órbita circular de raio R. A força centrípeta
sobre a nave é 1,5 GmM/R2 , onde G é a constante de gravitação universal e M a massa da
Terra.
a) Desenhe a trajetória dessa nave. Em um
ponto de sua trajetória, desenhe e identifique
os vetores velocidade v e aceleração centrípeta a da nave.
b) Determine, em função de M, G e R, os módulos da aceleração centrípeta e da velocidade da nave.
física 6
Resposta
Resposta
a) Considerando que a velocidade da espaçonave
tem módulo constante, sua trajetória é circular
como na figura a seguir.
a) Isolando os corpos e marcando as forças, vem:
Sendo a velocidade constante (R = 0), temos:
T = fat.A
⇒ F = fat.A + fat.B ⇒
F = T + fat.B
b) Do Princípio Fundamental da Dinâmica, vem:
1,5 G mM
= macp ⇒
R2
Rcp = macp ⇒
⇒
acp = 1,5
2
v2
=
⇒
R
R2
GM
µC = 0,60
T = µC mAg ⇒ T = 0,6 ⋅ 2,0 ⋅ 10,0 ⇒ T = 12,0 N
Sendo a aceleração centrípeta acp
1,5
⇒
b) SendoT = fat .A , vem:
GM
R
⇒ F = µC mAg + µC mB g ⇒
⇒ 18,0 = µC ⋅ 2,0 ⋅ 10,0 + µC ⋅ 1,0 ⋅ 10,0 ⇒
v =
v2
, vem:
=
R
1,5 G M
R
Observações:
1) Há uma contradição no enunciado ao dizer que
a espaçonave "gira em torno da Terra com velocidade constante". Na verdade, em um movimento
circular, o que pode se manter constante é o módulo da velocidade.
2) A resultante centrípeta fornecida pelo enunciado não pode ser gerada exclusivamente pela atração gravitacional terrestre.
Questão 15
Uma partícula A, com massa m = 0,2 kg, colide frontalmente com uma partícula B, com
massa maior que a de A, e que inicialmente se
encontra em repouso. A colisão é totalmente
elástica e a energia cinética final da partícula
A cai para 64% de seu valor inicial. Se a velocidade inicial da partícula A for v0 = 20,0 m/s,
calcule
a) a velocidade final da partícula A.
b) a quantidade de movimento da partícula B
após a colisão.
Questão 14
A figura ilustra um bloco A, de massa m A =
= 2,0 kg, atado a um bloco B, de massa mB =
= 1,0 kg, por um fio inextensível de massa
desprezível. O coeficiente de atrito cinético
entre cada bloco e a mesa é µc . Uma força F =
= 18,0 N é aplicada ao bloco B, fazendo com
que ambos se desloquem com velocidade
constante.
Considerando g = 10,0 m/s2 , calcule
a) o coeficiente de atrito µc .
b) a tração T no fio.
Resposta
a) A velocidade final v’ A da partícula A é dada por:
E’C A = 0,64 ⋅ EC A ⇒
= 0,64 ⋅
⇒
mA ⋅ v’02
=
2
mA ⋅ v A2
⇒ v’ A = 0,8v A = 0,8 ⋅ 20 ⇒
2
v’ A = 16 m/s
b) Dependendo da relação entre as massas de A
e B, após a colisão, A poderá manter ou inverter o
sentido do seu movimento.
• 1ª possibilidade: consideremos inicialmente
que A mantenha o sentido do seu movimento inicial. Do Princípio da Conservação da Quantidade
de Movimento, temos:
física 7
Qi = QF ⇒ mA ⋅ v 0 = mA ⋅ v’ A + QB ⇒
⇒ 0,2 ⋅ 20 = 0,2 ⋅ 16 + QB ⇒ QB = 0,8 kg ⋅ m/s (I)
Do enunciado, temos:
m ⋅v2
ECB = 0,36 EC A = 0,36 ⋅ A 0 ⇒
2
0,2 ⋅ 20 2
(II)
⇒ ECB = 0,36 ⋅
⇒ ECB = 14,4 J
2
m ⋅ v B2
(mB ⋅ v B ) 2
Sendo ECB = B
=
⇒
2
2mB
QB2
(III)
2mB
De (I), (II) e (III), obtemos:
3
D ⇒ µ = 0,75 g/cm 3
4
b) Na situação em que o bloco está preso no fio,
as forças que atuam sobre ele são dadas por:
⇒µ =
⇒ ECB =
0,8 2
⇒ mB = 2,2 ⋅ 10 −2 kg ⇒ mB < mA
2mB
Esse resultado contraria o enunciado. Assim a
partícula A não mantém o sentido do movimento
inicial.
• 2ª possibilidade: consideremos agora a situação em que A inverte o seu sentido de movimento.
Considerando positivo o sentido inicial do
movimento de A, do Princípio da Conservação da
Quantidade de Movimento, obtemos:
Qi = QF ⇒ mA ⋅ v 0 = mA ⋅ (−v’ A ) + QB ⇒
14,4 =
⇒ 0,2 ⋅ 20 = −0,2 ⋅16 + QB ⇒ QB = 7,2
kg ⋅ m
s
(IV)
De (II), (III) e (IV), obtemos:
7,2 2
⇒ mB = 1,8 kg
2mB
Assim mB > mA , concordando então com o enunciado.
⇒ T + 0,75 ⋅ 10 3 ⋅ 60 ⋅ 10 −6 ⋅ 10 =
= 10 3 ⋅ 60 ⋅ 10 −6 ⋅ 10 ⇒ T = 0,15 N
Questão 17
Uma quantidade de 1,5 kg de certa substância encontra-se inicialmente na fase sólida, à
temperatura de −20o C. Em um processo a
pressão constante de 1,0 atm, ela é levada à
fase líquida a 86o C. A potência necessária
nessa transformação foi de 1,5 kJ/s. O gráfico
na figura mostra a temperatura de cada etapa em função do tempo.
86
T (°C)
14,4 =
Do equilíbrio, vem:
T + P = E’ ⇒ T + µVg = DVg ⇒
Questão 16
Um bloco de madeira de volume V = 60 cm3 ,
totalmente submerso, está atado ao fundo de
um recipiente cheio de água por meio de um
fio de massa desprezível. O fio é cortado e o
bloco emerge na superfície, ficando com 1/4 de
seu volume fora da água. Sendo g = 10 m/s2 a
aceleração da gravidade e D = 1 g/cm3 a massa específica da água, calcule
a) a massa específica do bloco.
b) a tração no fio, antes de ser cortado.
Resposta
a) Na situação em que o bloco fica flutuando em
equilíbrio, temos:
3
DV
E = P ⇒ D ⋅ Vg = mg ⇒ 3
= µV ⇒
4
4
0
_20
0,7
6,2
t (min)
12,2
Calcule
a) o calor latente de fusão L f .
b) o calor necessário para elevar a temperatura de 1,5 kg dessa substância de 0 a 86o C.
Resposta
a) Para a fusão da substância, em um intervalo
∆t = (6,2 − 0,7)60 = 330 s, temos:
Q = m ⋅ Lf
⇒ m ⋅ L f = P ⋅ ∆t ⇒
Q = P ⋅ ∆t
física 8
⇒ 1,5 ⋅ L f = 1,5 ⋅ 330 ⇒ L f = 330
J
g
b) Para elevar a temperatura de 0 oC a 86 oC , em um
intervalo de tempo ∆t’ = (12,2 − 0,7) ⋅ 60 = 690 s,
temos:
Q = P ⋅ ∆t’ ⇒ Q = 1,5 ⋅ 690 ⇒ Q = 1 035 kJ
b) Sendo a imagem projetada sobre o filme invertida, pela equação da ampliação, temos:
y’máx.
p’
−36,0
52
=−
⇒
=−
⇒
y máx.
p
y máx.
1 300
⇒
y máx. = 900 mm
Questão 18
Questão 19
Uma câmara fotográfica rudimentar utiliza
uma lente convergente de distância focal
f = 50 mm para focalizar e projetar a imagem
de um objeto sobre o filme. A distância da
lente ao filme é p’ = 52 mm. A figura mostra o
esboço dessa câmara.
Uma luminária, com vários bocais para conexão de lâmpadas, possui um fusível de 5 A
para proteção da rede elétrica alimentada
com uma tensão de 110 V, como ilustrado na
figura.
5A
110 V
bocais
Para se obter uma boa foto, é necessário que
a imagem do objeto seja formada exatamente
sobre o filme e o seu tamanho não deve exceder a área sensível do filme. Assim:
a) Calcule a posição que o objeto deve ficar
em relação à lente.
b) Sabendo-se que a altura máxima da imagem não pode exceder a 36,0 mm, determine
a altura máxima do objeto para que ele seja
fotografado em toda a sua extensão.
Resposta
a) Pela equação da conjugação, temos:
1
1
1
1
1
1
=
+
⇒
=
+
⇒ p = 1 300 mm
f
p
p’
50
p
52
Calcule
a) a potência máxima que pode ser dissipada
na luminária.
b) o número máximo de lâmpadas de 150 W
que podem ser conectadas na luminária.
Resposta
a) A potência máxima é dada por:
Pmáx . = U ⋅ i = 110 ⋅ 5 ⇒ P = 550 W
b) Admitindo lâmpadas 110 V − 150 W (características nominais) ligadas corretamente, o número
máximo (n) de lâmpadas que podem ser conectadas sem que o fusível se queime é dado por:
⎢P
⎥ ⎢ 550 ⎥
n = ⎢ máx . ⎥ = ⎢
⇒
⎣ P ⎦ ⎣ 150 ⎥⎦
n = 3 lâmpadas