ponte wheatstone - Laboratórios de Engenharia Elétrica

EXPERIÊNCIA N◦ 01
PONTE WHEATSTONE
Fundação Universidade Federal de Rondônia
Núcleo de Tecnologia
Departamento de Engenharia Elétrica - DEE
Disciplina de Eletrônica II
I. O BJETIVOS
•
•
Conhecer e se familiarizar com dispositivos de identificação de resistores.
Manusear uma Ponte de Wheatstone e conhecer suas
características.
II. I NTRODUÇÃO
A ponte de Wheatstone é um aparelho elétrico usado como
medidor de resistências elétricas. Foi inventado por Samuel
Hunter Christie em 1833, porém foi Charles Wheatstone quem
ficou famoso com o invento, tendo-o descrito dez anos mais
tarde.
O circuito é composto por uma fonte de tensão, um
galvanômetro e uma rede de quatro resistores, sendo três
destes conhecidos. Para determinar a resistência do resistor
desconhecido os outros três são ajustados e balanceados até
que a corrente elétrica no galvanômetro caia a zero.
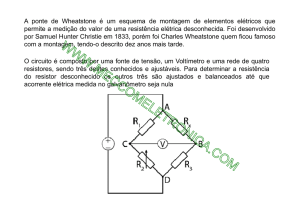
Figura 1.
Ponte de Wheatstone.
A. Aplicações
VAC
=
VAD
Medição de Resistência (década); Medição de Temperatura
(NTC, PTC); Medição de Pressão (Strain Gage); Medição de
Peso (Strain Gage).
Este tipo de circuito pode ser usado para se determinar a
tensão mecânica. Sendo Rx um resistor sensível a compressão
e os outros três resistores de valores conhecidos, a força
aplicada ao resistor variável será proporcional ao valor da
resistência desse resistor.
VCB
=
VDB
RS .i1
=
R1 .i2
RX .i1
=
R2 .i2
Dividindo uma equação pela outra temos:
R1
RS
=
R2
RX
B. Circuito e fórmula
A ponte de wheatstone é um método mais refinado de
se determinar a resistência de um resistor. Ela consiste na
utilização de um galvanômetro, dois resistores de resistência
conhecida (R1 e R2 ) e outro de resistência variável (RS ), além
de uma fonte de tensão.
A figura 1 mostra a montagem de uma ponte de Wheatstone:
Com a ponte equilibrada:
(1)
Numa ponte equilibrada, nota-se que há uma igualdade em
cruz do produto das resistências elétricas.
III. M ATERIAIS UTILIZADOS
•
•
•
•
•
Gerador de Tensão DC Instrutherm FA - 3030;
Multímetro;
Protoboard;
Resistores de 100Ω(2), 220Ω(1), 1kΩ(2) e 10kΩ(3);
Potenciômetros de 1kΩ(1), 10kΩ(2) e 100kΩ(3).
VAC
=
RS .i1
VAD
=
R1 .i2
IV. PARTE E XPERIMENTAL
A figura 2 mostra uma forma de determinação da resistência
elétrica, a qual requer um só medidor.
VCB
=
RX .i1
VDB
=
R2 .i2
2. Supondo que RS tenha uma escala calibrada, qual seria
a relação entre a resistência RX e o valor indicado de
RS ?
3. Pode-se imaginar uma forma mais sensível de determinação da posição zero do amperímetro? Apresente.
Consideremos o circuito da figura 4 com a chave fechada,
o ponteiro do amperímetro estará na posição central.
Figura 2.
Divisor de tensão com uma fonte.
Aqui, a resistência desconhecida Rx é usada num divisor
de tensão com um resistor padrão conhecido conectado através
de uma fonte de tensão VS conhecida. Assim:
RX
.VS
RS + RX
V
.RS
RX =
VS − V
Obviamente, RS , o resistor padrão, dever ser conhecido
de forma precisa. VS , a fonte de tensão, deve ser constante
e suficientemente precisa. O Voltímetro V deve ter uma
resistência elétrica muito superior a Rx para ter resultados
precisos.
Quando todo os valores do circuito forem conhecidos precisamente, a acuracidade final dependerá ainda da precisão do
medidor.
Seria vantajoso dispor de um método que não apresentasse
estas restrições. Consideremos a figura 3.
V
=
Figura 4.
Divisor de tensão com chave.
Quando a chave for aberta, qualquer corrente fluindo através
do amperímetro causará uma deflexão no ponteiro, indicando a
circulação de correntes, mesmo ínfimas. Este método constituise em uma das formas de boa sensibilidade.
4. A precisão da medida de resistência depende da acuracidade do amperímetro? Justifique.
5. A resistência do amperímetro afeta a precisão da medida? Justifique.
Uma das desvantagens de uso do circuito da figura 4 é
que ambas as fonte VS devem ser iguais em módulo. Isto
significa termos duas fontes precisas de tensão. Um método
que eliminasse este condicionante seria bem-vindo.
6. Com uma única fonte de tensão de V volts como poderia
ser possível montar um circuito tal que o amperímetro
seja conectado à um ponto de potencial V /2 Volts?
Figura 3.
Divisor de tensão com duas fontes.
Aqui nos teremos duas fontes de tensão de VS Volts. RS
é um resistor variável calibrado e RX a resistência desconhecida.
1. No circuito da figura 3 quando o medidor acusaria
leitura nula? Faça um gráfico com pelo menos 3 valores
diferentes de resistores incluindo o valor que causa
deflexão nula.
Figura 5.
Ponte Wheatstone.
Com R1 igual a R2 o potencial da conexão à esquerda do
amperíemtro será V /2 e com RS igual a RX o potencial no
lado direito da amperímetro também será V /2.
7. Qual será a leitura no amperímetro quando a chave for
aberta, com RS igual a RX ?
8. A precisão do amperímetro afeta a medida do resistor?
Justifique.
9. A precisão da fonte de tensão afeta a medida? Justifique.
10. A estabilidade da fonte afeta a medida? Justifique.
11. São os valores absolutos de R1 e de R2 que determinam
a precisão da medida RX , ou é a razão das resistências
que asseguram a precisão? Justifique.
R1 e R2 são frequentemente chamados de Razões dos
Braços do circuito, o qual é denominado Ponte de Wheatstone,
sendo desenhado na forma da figura 5.
Vamos investigar este tipo de circuito. Ajuste o circuito
da figura 5 com R1 = 10kΩ e R2 = 10kΩ. Use um
potenciômetro de 100kΩ para ajustar Rs .
Um resistor adicional de 220Ω deve ser incluído no circuito
em série com a ponte de Wheatstone para limitar a corrente
num risco de curto-circuito quando for energizada a montagem.
Lentamente aumente a tensão DC variável para suprir VS
com 10V . Conecte um resistor de aproximadamente 100Ω
nos terminais de RX e ajuste RS até alcançar equilíbrio no
amperímetro, ou seja, deflexão nula. Registre o valor de RS .
Desconecte o resistor de 100Ω, substituindo-o por um
de 1kΩ em RX . Repita o procedimento de equilíbrio do
amperímetro, registrando o novo valor de RS .
Repita o procedimento para R1 = 10kΩ.
12. Registre seus resultados na tabela I.
R1
10kΩ
R2
10kΩ
10kΩ
1kΩ
1kΩ
10kΩ
RX
100Ω
1kΩ
10kΩ
100Ω
1kΩ
10kΩ
100Ω
1kΩ
10kΩ
RS
Tabela I
Resultados.
13. Se a razão dos braços da Ponte mudar, tal que R1 =
10 ∗ R2 , qual seria a tensão na junção de R1 e R2 , com
relação à fonte de tensão?
14. Que razão de Rs para Rx daria o balanço neste caso?
15. Se R1 = R2 /10 qual seria a tensão na junção de R1
com R2 ?
16. Que relação de Rs para Rx resultaria no balanço agora?
Vamos checar as respostas.
Mude a relação dos braços para R1 = 10kΩ e R2 = 1kΩ
e repita as medidas para RX = 100Ω, RX = 1kΩ e RX =
10kΩ. Registre os resultados na tabela.
Mude a relação dos braços para R1 = 1kΩ e R2 = 10kΩ
e repita as medidas para RX = 100Ω, RX = 1kΩ e RX =
10kΩ. Registre os resultados na tabela.
17. A razão de RS para RX concorda com a de R1 para
R2 ?
R EFERÊNCIAS
[1] Wikipédia, “Ponte de Wheatstone”.
http://pt.wikipedia.org/wiki/Ponte_de_Wheatstone
[2] Thyago Ribeiro, “Ponte de Wheatstone”.
http://www.infoescola.com/eletricidade/ponte-de-wheatstone/
[3] Sedra, Adel S.; Smith, Kenneth C. “Microeletrônica”, 5a Edição. Editora
Pearson Prentice Hall, RJ - 2007.
[4] Boylestad, Robert L.; Nashelsky, Louis. “Dispositivos eletrônicos e teoria
de circuitos”, 8a Edição. São Paulo: Pearson Prentice Hall, 2004.