Slide 1 - Educacional

Mecânica
Cinemática
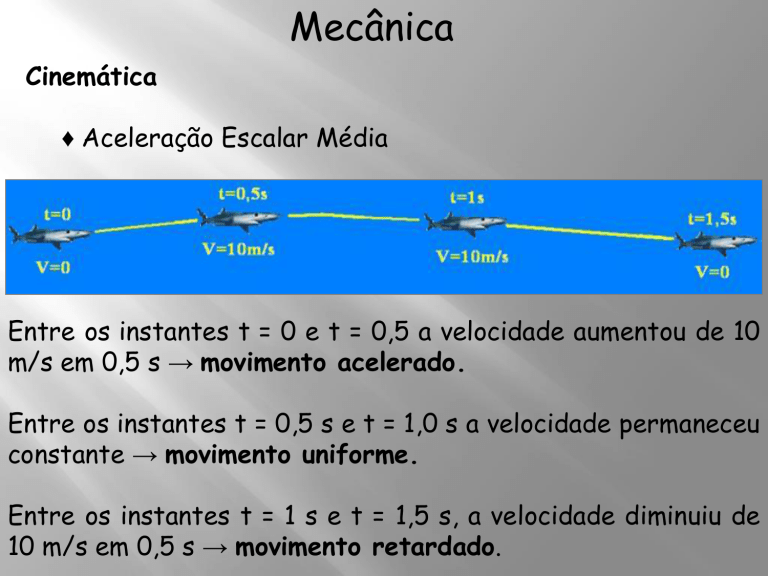
♦ Aceleração Escalar Média
Entre os instantes t = 0 e t = 0,5 a velocidade aumentou de 10
m/s em 0,5 s → movimento acelerado.
Entre os instantes t = 0,5 s e t = 1,0 s a velocidade permaneceu
constante → movimento uniforme.
Entre os instantes t = 1 s e t = 1,5 s, a velocidade diminuiu de
10 m/s em 0,5 s → movimento retardado.
Define-se aceleração escalar média (am) ao quociente entre a
variação de velocidade (ΔV) pelo respectivo intervalo de
tempo (Δt), ou seja:
A unidade de aceleração escalar média, no SI, é o m/s2
Classificação dos movimentos
Movimento
progressivo:
velocidade
positiva
deslocamento é no sentido dos marcos crescentes.
e
o
Movimento
retrógrado:
velocidade
negativa
deslocamento é no sentido dos marcos decrescentes.
e
o
Movimento acelerado: sempre que velocidade e aceleração
têm o mesmo sinal, ou seja, ambas são positivas ou ambas são
negativas, ou que o módulo da velocidade está aumentando.
Movimento retardado: sempre que velocidade e aceleração
têm sinais opostos, ou seja, quando um é positivo o outro é
negativo e vice-versa, ou que o módulo da velocidade está
diminuindo.
Exemplos
1 - (Unirio) Caçador nato, o guepardo é uma espécie de mamífero que
reforça a tese de que os animais predadores estão entre os bichos mais
velozes da natureza. Afinal, a velocidade é essencial para os que caçam
outras espécies em busca de alimentação. O guepardo é capaz de, saindo
do repouso e correndo em linha reta, chegar à velocidade de 72 km/h em
apenas 2,0 s. Determine a aceleração escalar média deste mamífero.
Resolução:
V = 72/3,6 = 20 m/s
am = (V - Vo) / (t – to)
am = (20 – 0) /(2 – 0)
am = 10 m/s2
2 - (FGV-SP) Um trem desloca-se com velocidade de 72 km/h, quando o
maquinista vê um obstáculo à sua frente.
Aciona os freios e pára em 4s. A aceleração média imprimida ao trem
pelos freios, foi em módulo, igual a:
a) 18 m/s2
b) 10 m/s2
Resolução:
V = 72/3,6 = 20 m/s
am = (V - Vo) / (t – to)
am = (0 – 20) / (4 – 0)
am = - 5 m/s2
Alternativa c
c) 5 m/s2
d) 4 m/s2
e) zero
Movimento Uniformemente Variado
♦ Aceleração Instantânea Constante
♦ Aceleração Instantânea = Aceleração Média
♦ am = a = ΔV/Δt
♦ Função horária da velocidade
♦ V = V0 + a.t
♦ Gráfico V x t do MUV
♦ Gráfico a x t do MUV
Exemplos
1 - (UFB) Um gato realiza um MUV em trajetória retilínea e horizontal
que obedece à função horária da velocidade V = - 20 + 5t em unidades do
SI. Pede-se:
a) a velocidade inicial e a aceleração
b) o instante em que ele muda o sentido de seu movimento
c) classificar o movimento em progressivo ou retrógrado, acelerado ou
retardado, orientando a trajetória para a direita.
Resolução:
a) V = V0 + at / V = - 20 + 5t → V0 = - 20 m/s e a = 5 m/s2
b) Quando ele muda o sentido de seu movimento ele pára (V = 0)
V = - 20 + 5t → 0 = - 20 + 5t → t = 4 s
c) De 0 a 4 s → V < 0 e a > 0 → retrógrado e retardado
A partir de 4 s → V > 0 e a > 0 → progressivo e acelerado
2 - (UFSM-RS) Ao preparar um corredor para uma prova rápida, o
treinador observa que o desempenho dele pode ser descrito, de forma
aproximada, pelo seguinte gráfico:
A velocidade média desse corredor, em m/s, é de:
a) 8,5
b) 10,0
c) 12,5
d) 15,0
Resolução:
ΔS = área = (10 + 6).12,5 / 2 → ΔS = 100 m
Vm = ΔS / Δt → Vm = 10 m/s
Alternativa b
e) 17,5
3 - (PUC-RJ) Considere o movimento de um caminhante em linha reta.
Este caminhante percorre os 20,0 s iniciais à velocidade constante v1 =
2,0 m/s. Em seguida, ele percorre os próximos 8,0 s com aceleração
constante a = 1 m/s2. Calcule a velocidade final do caminhante.
Resolução:
Vo = 2 m/s / a = 1 m/s2
V = Vo + at V=2 + 1.8 → V = 10 m/s
4 – (UFRJ) Um avião vai decolar em uma pista retilínea. Ele inicia seu
movimento na cabeceira da pista com velocidade nula e corre por ela com
aceleração média de 2,0 m/s2 até o instante em que levanta vôo, com uma
velocidade de 80 m/s, antes de terminar a pista. Calcule quanto tempo o
avião permanece na pista desde o início do movimento até o instante em
que levanta vôo.
Resolução:
V = Vo + at
80 = 0 + 2.t
T = 40 s
Movimento Uniformemente Variado
♦ Função horária da velocidade
♦ S = S0 + V0t + a.t2/2
♦ Equação de Torricelli
♦ V2 = V02 + 2aΔS
Exemplos
1 - (UNESP-SP) Um veículo está rodando à velocidade de 36 km/h numa
estrada reta e horizontal, quando o motorista aciona o freio. Supondo
que a velocidade do veículo se reduz uniformemente à razão de 4 m/s em
cada segundo a partir do momento em que o freio foi acionado,
determine:
a) o tempo decorrido entre o instante do acionamento do freio e o
instante em que o veículo pára.
b) a distância percorrida pelo veículo nesse intervalo de tempo.
Resolução:
a) So = 0 / Vo = 36/3,6 = 10 m/s / a = ΔV/Δt = - 4/1 = - 4 m/s2
Pára (V = 0) → V = Vo+ at → 0 = 10 - 4t
t = 2,5 s
b) S = So + Vot + at2/2 → S - So = Vot + at2/2
ΔS = 10.2,5 – 4.(2,5)2/2 → ΔS = 25 – 12,5
ΔS = 12,5 m
2 - (UNESP) Em um determinado instante, um carro que corre a 100
km/h em uma estrada horizontal e plana começa a diminuir sua
velocidade, com o módulo da aceleração constante. Percorrido 1 km, a
redução da velocidade é interrompida ao mesmo tempo em que o carro é
detectado por um radar fotográfico. O radar mostra que o carro está na
velocidade limite permitida de 80 km/h. Assim, pede-se o módulo da
aceleração, em m/s2, durante o intervalo de tempo em que a velocidade
do carro diminuiu de 100 km/h para 80 km/h.
Resolução:
Vo = 100 km/h / V = 80 km/h / ΔS = 1 km
V2 = Vo2 + 2.a.ΔS
6400 = 10000 + 2.a.1
a = - 1800 km/h2
a = - 1800.1000/36002
a = - 0,14 m/s2
3 - (FUVEST) A velocidade máxima permitida em uma auto-estrada é de
110 km/h e um carro, nessa velocidade, leva 6 s para parar
completamente. Diante de um posto rodoviário, os veículos devem
trafegar no máximo a 36 km/h. Assim, para que carros em velocidade
máxima consigam obedecer o limite permitido, ao passar em frente do
posto, a placa referente à redução de velocidade deverá ser colocada
antes do posto, a uma distância, pelo menos, de:
a) 40 m
b) 60 m
c) 80 m
d) 90 m
e) 100 m
Resolução:
Vo = 110/3,6 = 30 m/s
V = Vo + at → 0 = 30 + a.6 → a = - 5 m/s2
Com essa aceleração sua velocidade deve ser reduzida de V0 = 30 m/s
para V = 10 m/s
V2 = Vo2 + 2.a.ΔS → 100 = 900 – 2.5.ΔS → ΔS = 80 m
Alternativa c
4 - (PUC-RJ) Dois objetos saem no mesmo instante de dois pontos A e B
situados a 100 m de distância um do outro. Os objetos vão se encontrar
em algum ponto entre A e B. O primeiro objeto sai de A em direção a B,
a partir do repouso, com uma aceleração constante igual a 2,0 m/s2. O
segundo objeto sai de B em direção a A com uma velocidade constante
de v = 15 m/s. Determine a posição onde ocorre o encontro dos dois
objetos, medido a partir do ponto A.
Resolução:
A → MUV → a = 2 m/s2 / Vo = 0 / So = 0
SA = So + Vo.t + a.t2/2 → SA = 0 + 0.t + 2.t2/2 → SA = t2
B → MU → V = -15 m/s / So = 100 m
SB = So + V.t → SB = 100 – 15.t
No encontro : SA = SB → t2 = 100 – 15t → t2 + 15t – 100 = 0
t = 5 s (instante do encontro)
Substituindo t = 5 s em SA = t2 → SA = 52 → SA = 25 m
4 - (UFG) A pista principal do aeroporto de Congonhas em São Paulo
media 1940 m de comprimento no dia do acidente aéreo com o Airbus
320 da TAM, cuja velocidade tanto para pouso quanto para decolagem é
259,2 km/h. Após percorrer 1240 m da pista o piloto verificou que a
velocidade da aeronave era de 187,2 km/h. Mantida esta desaceleração,
a que distância do fim da pista o piloto deveria arremeter a aeronave,
com aceleração máxima de 4 m/s2, para evitar o acidente?
a) 312 m
b) 390 m
Resolução:
c) 388 m
d) 648 m
V0 = 259,2/3,6 = 72 m/s / V = 187,2/3,6 = 52 m/s
V2 = Vo2 + 2.a.ΔS → 522 = 722 + 2.a.1240 → a = -1 m/s2
Distância de desaceleração será ΔS = 1940 – Δx
V2 = 722 - 2.(1940-Δx) (no trecho de frenagem)
722 = V2 + 2.4.Δx (no trecho de aceleração)
722 = 722 - 2.(1940 - Δx) + 8Δx → 0 = - 3880 + 2Δx + 8Δx
3880 = 10.Δx → Δx = 3880/10 = 388 m
Alternativa c
e) 700 m
5 - O movimento de uma bola sobre uma trajetória retilínea é descrito
de acordo com a seguinte equação: x = 5 + 16t - 2t2, em que x é medido
em metros e t em segundos.
a) Faça o esboço do gráfico da posição em função do tempo.
Resolução:
a)
b) Calcule a velocidade da bola em t = 4,0 s.
Resolução:
Se S = 5 + 16.t - 2.t2 temos v = 16 - 4.t → v = 16 - 4.4 = 16 - 16 = 0 m/s
c) Calcule a distância percorrida pela bola e o seu deslocamento em t =
5,0 s.
Resolução:
t = 0 → So = 5 m
t = 5 s → S = 5 + 16.5 - 2.25 → S5 = 35 m
ΔS = S5 – So = 35 – 5 = 30 m
V = Vo +a.t → 0 = 16 – 4t → t = 4 s
S4 = 5 + 16.4 - 2.16 = 37 m
d = 37 – 5 + 2 → d = 34 m
Exercícios
1 - (PUC) Um corredor olímpico de 100 metros rasos acelera desde a
largada, com aceleração constante, até atingir a linha de chegada, por
onde ele passará com velocidade instantânea de 12 m/s no instante final.
Qual a sua aceleração constante, em m/s2 ?
a) 10,0
b) 1,0
c) 1,66
d) 0,72
e) 2,0
2 - (UFPR) Um motorista conduz seu automóvel pela BR-277 a uma
velocidade de 108 km/h quando avista uma barreira na estrada, sendo
obrigado a frear (desaceleração de 5 m/s2) e parar o veículo após certo
tempo. Pode-se afirmar que o tempo e a distância de frenagem serão,
respectivamente:
a) 6 s e 90 m b) 10 s e 120 m c) 6 s e 80 m
d) 10 s e 200 m
3 - (PUC) Um atleta corre a uma certa velocidade constante em linha
reta e ultrapassa um carro que está sendo acelerado (a = 2,0 m/s2) do
repouso na mesma direção e sentido. O instante de tempo t = 0 é o tempo
inicial de aceleração do carro e também o instante de tempo em que o
atleta passa pelo carro. O atleta consegue se manter à frente do carro
por 3,0 s. Qual é a velocidade do atleta?
a) 1,0 m/s
b) 3,0 m/s
c) 7,0 m/s
d) 9,0 m/s
e) 11,0 m/s
1 – Resolução:
Vo = 0 / V = 12 m/s / ΔS = 100 m
V2 = Vo2 + 2.a.ΔS → 122 = 2.a.100 → a = 144/200 → a = 0,72 m/s2
Alternativa d
2 – Resolução:
Vo = 108 km/h = 30 m/s / a = - 5 m/s2
Tempo de frenagem: V = Vo + a t → 0 = 30 – 5 t → t = 6 s
Distância de frenagem: V2 = Vo2 + 2.a.ΔS → 0 = 302 + 2 (- 5)ΔS
10.ΔS = 900 → ΔS = 90 m
Alternativa a
3 – Resolução:
Carro (MUV): Sc = So + Vot + at2/2 = 0 + 0 + 2t2/2 → Sc = t2
Atleta (MU): Sat = So + V.t = 0 + Vt → Sat = Vt
Se o atleta se mantém na frente do carro por t = 3 s
Sat = Sc, quando t = 3 s → Vt = t2 → V.3 = 32 → V = 3 m/s
Alternativa b