1/4
Derivadas
Outras funções:
y
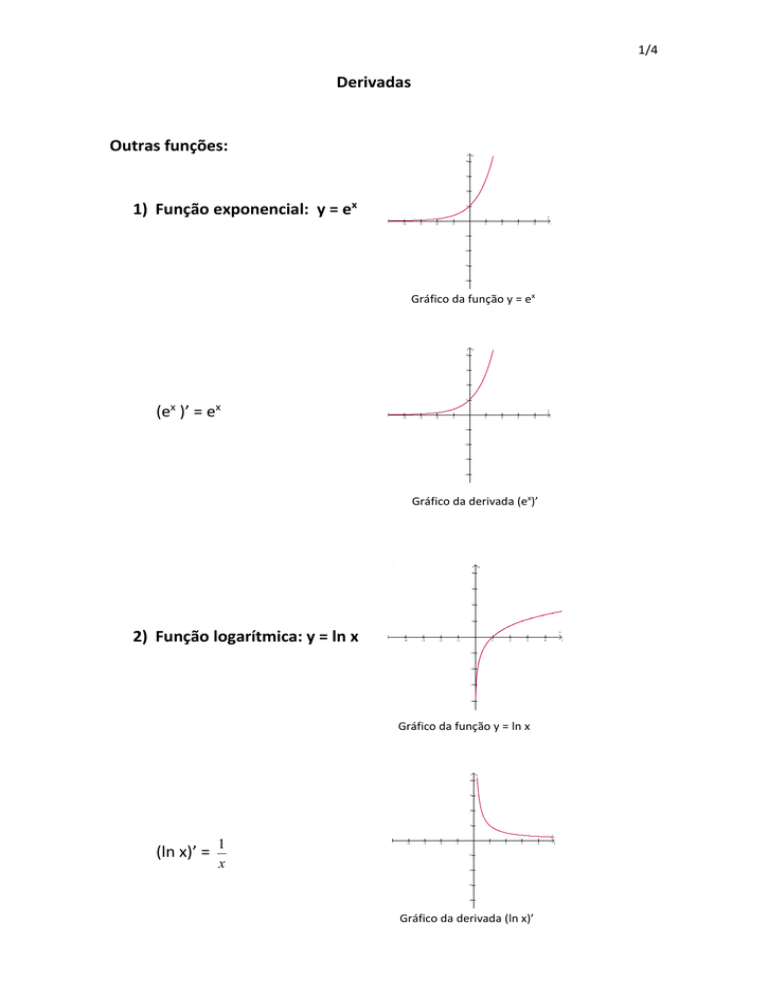
1) Função exponencial: y = ex
x
Gráfico da função y = ex
y
x
x
(e )’ = e
x
Gráfico da derivada (ex)’
y
2) Função logarítmica: y = ln x
x
Gráfico da função y = ln x
y
x
1
(ln x)’ =
x
Gráfico da derivada (ln x)’
2/4
3) Funções trigonométricas:
y
a) Função seno: y = sen x
x
Gráfico da função y = sen x
y
x
(sen x)’ = cos x
Gráfico da derivada (sen x)’
y
b) Função cosseno: y = cos x
x
Gráfico da função y = cos x
y
(cos x)’ = - sen x
x
Gráfico da derivada (cos x)’
3/4
c) Função tangente: y = tg x =
(tg x)’ =
senx
cos x
cos x.( senx )' senx.(cos x)' cos x. cos x senx.( senx)
=
cos 2 x
(cos x) 2
1
cos 2 x sen 2 x
1
2
(tg x)’ =
=
=
= sec x
2
2
cos
x
cos
x
cos x
2
d) Função cotangente: y = cotg x =
cos x
senx
(cotg x)’ =
senx.(cos x)' cos x.( senx)' senx.( senx) cos x.(cos x)'
=
sen 2 x
( senx) 2
(cotg x)’ =
1
1
sen 2 x cos 2 x ( sen 2 x cos 2 x)
=
=
=
2
2
2
sen x
sen 2 x
sen x
sen x
1
(cotg x)’ =
senx
2
= cos sec 2 x
e) Função secante: y = sec x =
(sec x)’ =
1
cos x
1 senx
cos x.1'1.(cos x)' 0 1.( senx) 1.senx
.
=
=
=
2
2
2
cos x cos x
(cos x)
(cos x)
(cos x)
(sec x)’ = sec x.tgx
4/4
f) Função cossecante: y = cossec x =
(cossec x)’ =
1
senx
1 cos x
senx.1'1.( senx )' 0 1. cos x
.
=
=
2
2
senx senx
( senx )
( senx )
(cossec x)’ = cos sec x. cot gx
Exercícios
1) Calcular as derivadas de:
1
x
a) f ( x) ln x e x → f ' ( x) e x
1
x
b) f ( x) 5 ln x 2e x → f ' ( x) 5. 2e x
c) f ( x) 6senx 3tgx → f ' ( x) 6 cos x 3 sec 2 x
d) f ( x)
1
cot gx
1
cos sec 2 x
cos x
→ f ' ( X ) senx
3
2
3
2
e) f ( x) 10 sec x
cos sec x
cos sec x. cot gx
→ f ' ( x) 10 sec x.tgx
4
4
f) f ( x) e x .tgx → f ' ( x) e x . sec 2 x
g) f ( x) 5 ln x 2 cos sec x → f ' ( x)
5
2 cos sec x. cot gx
x
h) f ( x)
ln x
1
→ f ' ( x)
x
e
x.e x
i) f ( x)
cos x 2senx
senx 2 cos x
→ f ' ( x)
sec 2 x
tgx
j) f ( x) senx.5 cos sec x → f ' ( x) 5 cos x. cos sec x. cot gx
