COB781- Princípios de Instrumentação

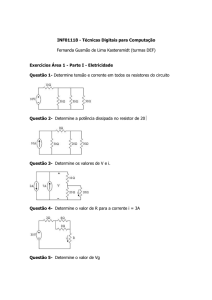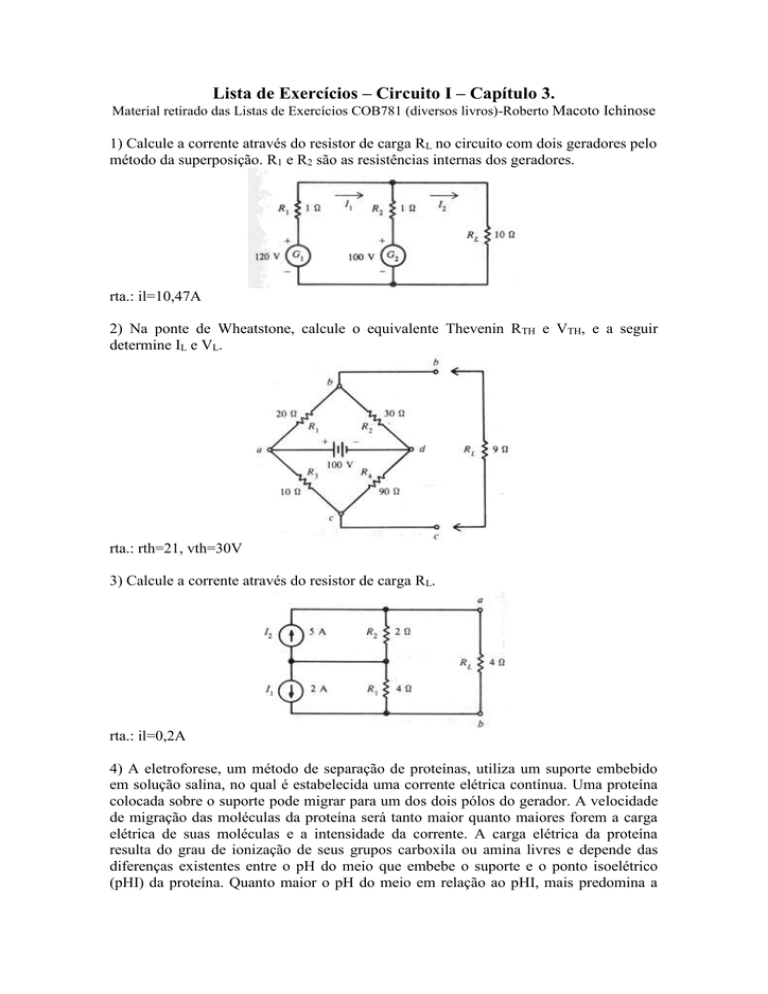
Lista de Exercícios – Circuito I – Capítulo 3.
Material retirado das Listas de Exercícios COB781 (diversos livros)-Roberto Macoto Ichinose
1) Calcule a corrente através do resistor de carga RL no circuito com dois geradores pelo
método da superposição. R1 e R2 são as resistências internas dos geradores.
rta.: il=10,47A
2) Na ponte de Wheatstone, calcule o equivalente Thevenin RTH e VTH, e a seguir
determine IL e VL.
rta.: rth=21, vth=30V
3) Calcule a corrente através do resistor de carga RL.
rta.: il=0,2A
4) A eletroforese, um método de separação de proteínas, utiliza um suporte embebido
em solução salina, no qual é estabelecida uma corrente elétrica contínua. Uma proteína
colocada sobre o suporte pode migrar para um dos dois pólos do gerador. A velocidade
de migração das moléculas da proteína será tanto maior quanto maiores forem a carga
elétrica de suas moléculas e a intensidade da corrente. A carga elétrica da proteína
resulta do grau de ionização de seus grupos carboxila ou amina livres e depende das
diferenças existentes entre o pH do meio que embebe o suporte e o ponto isoelétrico
(pHI) da proteína. Quanto maior o pH do meio em relação ao pHI, mais predomina a
ionização da carboxila sobre a da amina e vice-versa. O pHI é definido como o pH do
meio onde a carga da proteína é nula.
Observe, abaixo, os esquemas de quatro circuitos elétricos de corrente contínua,
disponíveis para uso na eletroforese das proteínas. Considere a resistência interna do
gerador nula.
Se a intensidade da corrente elétrica no suporte de eletroforese for superior a 0,2 A, a
quantidade de calor dissipada no suporte será capaz de promover a desnaturação térmica
das proteínas a serem separadas. Dentre os quatro circuitos disponíveis, qual é aquele
que permitiria a maior velocidade de migração, sem acarretar a desnaturação das
proteínas ? Justifique.
rta.: IV
5) Calcule a corrente elétrica em cada resistor.
rta.: i1=9A, i2=6A, i3=3A, i4=2A, i5=1A.
6) Calcule a tensão no ponto A.
rta.: va=-1,15V
7) Utilizando o método das malhas, monte o sistema de equações que permita calcular
I1, I2 e I3.
8) Ache a resistência equivalente do circuito a seguir:
rta.: req=2R
9) Calcule a resistência equivalente RT e a tensão de saída Vo do circuito a seguir.
10) Qual é a corrente no resistor R6 no circuito abaixo?
rta.: i=6A
11) Calcule a tensão v indicada no circuito.
rta.: v=26V
12) Substitua o circuito à esquerda dos pontos ab pelo seu equivalente Thévenin.
rta.: vth=180V, rth=0
13) Determine a corrente i indicada no circuito a seguir:
rta.: i=1,5A
14) Escolha o valor de R para que a diferença de tensão entre os pontos A e B seja zero.
rta.: R=25
15) No circuito abaixo, calcule a corrente indicada por uma seta.
rta.: Ix=6/19 A
16) Calcule o valor dos resistores para que, do ponto de vista dos terminais A, B e C as
duas redes resistivas sejam equivalentes.
rta.: Rx=(R4·R5+R6·R5+R4·R6), R2=Rx/R5, R1=Rx/R6 e R3=Rx/R4
Ry=(R1+R2+R3), R4=(R1·R2)/Ry, R5=(R1·R3)/Ry, R6=(R2·R3)/Ry
17) Recalcular o problema 9 utilizando o resultado obtido no problema 16.
18) Considerando o diodo ideal esboçe o gráfico no tempo das tensões no resistor (v1) e
no diodo (v2) do circuito a seguir.
19) Considerando o diodo do circuito abaixo ideal, esboçe a forma de onda v(t). (Obs: o
diodo é um elemento não linear, dessa forma não utilize a técnica de superposição).
20) A tensão em um indutor de 0,5H é dada pelo gráfico a seguir, esboçe o gráfico da
corrente no indutor.
Lista de Exercícios – Circuito I – Capítulo 3.
Material retirado das Listas de Exercícios de Eletricidade A – UFRGS – John Wisbeck
(O atalho para as questões originais está na seção consulta – links úteis)
1) A figura 1 apresenta o símbolo utilizado para representar uma classe de bipolos
conhecida como diodos. A relação v-i de um diodo de junção pn é mostrado na figura 1.
Determine o modelo, com base em elementos básicos ideais, capaz de representar o
diodo, da forma mais aproximada possível, dentro das faixas de tensão e corrente
indicadas (entre 0,7V e 0,75V e entre 0,5A e 2A).
i
Amperes
i
2,0
1,5
+
v
D1
1,0
0,5
Diodo
0
_
0,7 0,75
v
volts
Figura 1
2) No circuito apresentado na figura 2, observe as informações fornecidas no circuito e
determine a variável desconhecida vx
ix
R1
400
R3
80
+
V1
R2
100
I1
135mA 10mA
R9
R5
300
R6
400
R4
1k
+
V2
5V
-
R7
250
R8
250
+
vx
_
Figura 2
3) No circuito apresentado na figura 2 determine o valor da corrente ix.
4) No circuito apresentado na figura 3, determine o valor da tensão vx.
R2
6
4V
+
+ V1
19V
R5
R6
I1
R3
8
+
R8
10
R7 R4
6
Figura 3
vx
-
5) No circuito apresentado na figura 4, determine o valor da corrente ix.
R4
40
R2
6
+ 15V -
+
I1
V1
R3
8
R5
ix
R8
10
R7
R6
Figura 4
6) No circuito apresentado na figura 5, determina o valor da tensão vx e da corrente ix.
R6
80
ix
R5
100
R4
400
+
R12
R3
+
10mA
R7
30
vx
_
V1
50V
R10
1500
R8
40
-
R9
50
R11
Figura 5
7) No circuito da figura 6 determine a variável desconhecida ix.
Resto do
Circuito
20mA
R2
2k
R5
1k
I1
R4 100mA
R1
-40V +
+
ix
V1
10V
-
Figura 6
R3
4k
8) No circuito da figura 7, determine a matriz de recorrência A e a matriz B que
permitem determinar as correntes indicadas no circuito.
i2
i3
R2
3
i1
R3
4
R4
5
+
I2
2A
I1
3A R1
20
+
R5
2
R6
4
-
V2
15V
i1 
 
1
i2   A B
i3 
V1
10V
-
Figura 7
9) No circuito da figura 8, determine a matriz de recorrência A e a matriz B que
permitem determinar as correntes indicadas no circuito.
i3
R4
6
+
I1
3A
V1
10V
- R1
3
i1
R5
10
i4
R2
5
i2
I2
2A
R3
8
i1 
 
i2   A 1 B
i3 
 
i4 
Figura 8
10) No circuito da figura 9 determine as potências nas fontes de energia seguindo a
convenção passiva.
R1
1k
I1
10mA
+
R2
1k
V1
10V
-
Figura 9
11) No circuito da figura 10, determine a matriz A que permite determinar as correntes
indicadas no circuito.
i4
R1
4
R2
7
I2
1A
I1
2A
i2
R5
5
-
+
V2
1V
i3
R4
2
Figura 10
i1
R3
5
+
-
V1
10V
i1 
 
i2   A 1 B
i3 
 
i4 
12) Empregando apenas técnicas de redução de circuitos determine a tensão "vx" no
circuito da figura 11
R4
6
+ vx -
+
I1
3A
V1
10V
- R1
3
I2
2A
R3
8
R5
10
R2
5
Figura 11
13) Empregando apenas técnicas de redução de circuitos determine a tensão "vx" no
circuito da figura 12
R6
5
R7
4
+ vx -
R1
5
I2
1A
+
R5
4
V1
15V
-
+
R2
3
I1
R3
7
R4
6
V1
10V
-
Figura 13
14) No circuito da figura 14 (que é um circuito linear), a tensão vx é 2V. Qual o novo
valor de vx se o valor de todas as fontes de tensão e corrente do circuito tiverem seus
valores dobrados? Justifique sua resposta com base no princípio da linearidade
Resto do Circuito
R4
Não possui fontes Independentes
+ vx -
Todos os elementos são lineares
-
+
10V
R1
1k
10
1A
5
R
Figura 14
15) No circuito da figura 14 qual o valor de vx se a fonte de tensão passar para 20V e a
de corrente para 0,5A?
a) 1,5V
b) Não é possível calcular (porque?)
c) 2,5V
d) 0V
e) Só é possível calcular se forem conhecidos os valores de R4 e R
16) Determine o equivalente de Norton do circuito da figura 15, sabendo que: quando
uma resistência de 20 ohms foi ligada aos terminais a e b a tensão vab é de 10V e que
quando foi ligada uma fonte de tensão de 30V entre os terminais a e b a corrente que
atravessou a fonte indo do positivo para o negativo da fonte foi de 3A. Desenhe o
circuito equivalente e indique os valores dos componentes e a posição dos terminais a e
b.
a
b
Figura 15
Lista de Exercícios – Circuito I – Capítulo 3.
Material retirado de provas de EEL420 – Professor Antonio Petraglia
1) Por um capacitor de 4F, com sentido de referência passivo para tensão e corrente,
circula uma corrente que varia com o tempo da seguinte forma: a) Para   < t < 0 a
corrente vale zero; b) Para 0  t < 2 a corrente vale 2A; c) Para 2  t < 3 a corrente
vale -1A; d) Para t>3 a corrente vale 0A. Determine a forma de onda da corrente e da
tensão sobre o capacitor para t>0. Considere que vc 0 - = 1V .
 
2) Um elemento caracterizado no plano tensão (V) x corrente (A) pela equação
v = 2  i +10 , é conectado em paralelo com um resistor de 2. Calcule:
a) A tensão e a corrente sobre o resistor.
b) As potências em Watts no resistor e no elemento.
rta.: a) 2,5A, 5V; b)Pelemento=–12,5W e Presistor= +12,5W
3) Um capacitor de 2pF, inicialmente descarregado, é conectado em paralelo com uma
fonte de corrente constante Is em t=0. Calcule:
a) O valor de Is de forma que o capacitor se carregue com 2,5V no intervalo de 10ns.
b) A energia em Joules entregue pela fonte ao capacitor nesse intervalo.
rta.: a) Is=0,5mA; b) w=6,25pJ