Técnicas de Otimização

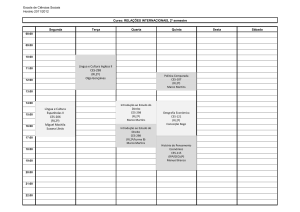
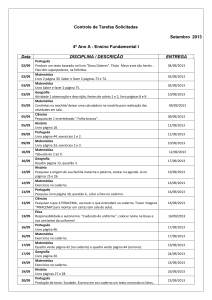
Técnicas de Otimização
1) Definição: buscam minimizar ou maximizar uma função através da escolha dos valores de
variáveis reais ou inteiras dentro de um conjunto possível visando encontrar uma solução
ótima para um dado problema.
Subestrutura ótima: um problema apresenta subestrutura ótima se uma solução ótima para o
problema contém dentro dela soluções ótimas para subproblemas. Propriedade chave para se
avaliar a possibilidade de aplicação de programação dinâmica e algoritmos gulosos.
a) Algoritmos Gulosos: (propriedade de escolha gulosa): uma solução globalmente ótima
pode ser alcançada fazendo-se uma escolha localmente ótima (gulosa). Em outras palavras,
quando estamos considerando que escolha fazer, efetuamos a escolha que parece melhor no
problema atual, sem considerar resultados de subproblemas. Estes algoritmos são eficientes
em alguns problemas de otimização.
b) Programação Dinâmica: diferem dos Algoritmos Gulosos, pois a escolha em cada passo
pode depender das soluções de subproblemas. A programação dinâmica permite transformar
recursão em iteração armazenando soluções de subproblemas em uma tabela.
2) Exemplo: Soluções para o problema da mochila
Descrição: temos que carregar uma mochila de capacidade limitada com diversos produtos de
pesos e valores diferentes. Como devemos fazer para carregar o maior valor possível em
produtos, respeitando a capacidade da mochila?
Este problema apresenta duas versões, uma contínua e outra booleana. Enquanto na contínua
consideramos ser possível carregar frações dos produtos, na booleana carregamos apenas o
produto inteiro. Este problema é um dos 21 problemas NP-completos de Richard Karp,
descritas no seu artigo de 1972.
2.1) Formulação:
Considere:
n: quantidade de produtos
W: capacidade da mochila
v[n]: vetor contendo o valor dos produtos
w[n]: vetor contendo o peso dos produtos
x[n]: vetor resultante, ou mochila resultante.
x.w : produto escalar x[1]w[1] + . . . + x[n]w[n].
Assim, uma mochila é qualquer vetor x[1..n] tal que
x·w  W
e
0  x[i]  1 para todo i.
O valor de uma mochila x é obtido pelo produto escalar x·v. Na versão booleana vale a
restrição: x[i] = 0 ou x[i] = 1.
2.2) Algoritmo Guloso - Versão Contínua da Mochila
Os dados devem ser fornecidos em ordem decrescente de v/w:
v[1]/w[1]  v[2]/w[2]  . . .  v[N]/w[N]
MOCHILA-CONTÍNUA (w, v, W, n)
início
j = 1;
enquanto (j <= n e w[j] <= W) faça
x[j] = 1;
W = W-w[j];
j = j+1;
fimenquanto
se (j <= n) então
x[j] = W/w[j];
fimse
para k = j+1 até n faça
x[k] = 0;
fimpara
escreva(x);
fim.
void mochila_continua(int *w, int *v, int W,
int n, float *x) {
int j, k;
j=1;
while (j<=n && w[j]<=W) {
x[j]=1;
W=W-w[j];
j=j+1;
}
if (j<=n) x[j]=W/w[j];
for(k=j+1; k<=n; k++) x[k]=0;
for(j=1;j<=n; j++)
printf("%.2f\n", x[j]);
}
Outra possível solução:
MOCHILA-CONTÍNUA (w, v, W, n)
inicio
para j de 1 até n faça
se (w[j] <= W)
então x[j] = 1;
W = W-w[j];
senão x[j] = W/w[j];
W = 0;
fimse
fimpara
escreva(x);
fim.
void mochila_continua(int *w, int *v, int W,
int n, float *x) {
int i;
for(i=1; i<=n; i++) {
if (w[i]<=W) {
x[i]=1;
W=W-w[i];
} else {
x[i]= (float) W/w[i];
W=0;
}
}
for(i=1;i<=n; i++)
printf("%.2f\n", x[i]);
}
O algoritmo guloso escolhe o primeiro objeto viável (na ordem dada) e não se preocupa com
o futuro e nem pode voltar atrás sobre um valor atribuído a um componente de x. Consumo de
tempo O(n), sem considerar o tempo O(n log(n)) necessário para ordenar os objetos antes de
aplicar o algoritmo.
2.3) Algoritmo Recursivo – Mochila Booleana
O algoritmo guloso não funciona para a versão booleana do problema da mochila. Uma
possibilidade está em uma versão recursiva que retorna o valor x.v de uma mochila de valor
máximo.
MOCHILA-Bool (w, v, n, W)
início
se (n == 0)
então retorne 0;
senão A = MOCHILA-Bool (w, v, n-1, W)
se (w[n] > W)
então devolva A
senão B = MOCHILA-Bool (w,
v, n-1, W-w[n]) + v[n]
retorne max(A,B);
fimse
fimse
fim
int mochila_rec(int *w, int *v, int n, int W) {
int A, B;
if (n==0) return 0;
else {
A=mochila_rec(w, v, n-1, W);
if (w[n]>W) return A;
else {
B=mochila_rec(w, v, n-1,
W- w[n]) + v[n];
return max(A,B);
}
}
}
Na literatura observa-se que este algoritmo é muito ineficiente uma vez que refaz, várias
vezes, a solução de vários dos subproblemas. Uma possível solução está na programação
dinâmica.
2.5) Algoritmo de Programação Dinâmica - Mochila Booleana
Considere a tabela para armazenamento dos subproblemas como t[n, W], onde t[i,j] é o valor
máximo da expressão x[1..i]·v[1..i] sujeita à restrição
x[i]·w[i] <= j.
0in e 0jW
Considere t[0,Y]=0 para todo Y. Se i > 0 então temos a recorrência:
t[i,j] = A
t[i,j] = max(A,B)
se w[i]>j e
se w[i]<= j,
onde A = t[i-1,j] e B = t[i-1,j-w[i]] + v[i].
O consumo de tempo do algoritmo é O(nW).
MOCHILA-BOOLEANA (w, v, n, W)
inicio
para Y de 0 até W faça
t[0,Y] = 0;
para i de 1 até n faça
A = t[i-1,Y];
se (w[i] > Y)
então B = 0;
senão B = t[i-1,Y-w[i]] + v[i];
fimse
t[i,Y] = max (A,B);
fimpara
fimpara
Y = W;
para i de n até 1 passo -1 faça
se t[i,Y] = t[i-1,Y]
então x[i] := 0
senão x[i] := 1
fimse
Y := Y-w[i];
fimpara
escreva(t);
fim.
3) Aplicações da Programação Dinâmica
3.1) Reconhecimento de Padrões
- Exemplo Algoritmo de Viterbi
3.2) Distância de Edição
- Comparação de cadeias
int ** mochila_booleana_pd(int *w, int *v,
int n, int W, float *x){
int **t, i, y, A, B;
t=create(n, W);
for(y=0; y<=W; y++) {
t[0][y]=0;
for(i=1; i<=n; i++) {
A=t[i-1][y];
if (w[i]>y) B=0;
else B=t[i-1][y-w[i]] + v[i];
t[i][y]=max(A,B);
}
}
y=W;
for(i=n; i>=1; i--) {
if (t[i][y]==t[i-1][y]) x[i]=0;
else x[i]=1;
y=y-w[i];
}
return t;
}