Correcção da ficha …já corrigida

FICHA DE TRABALHO - Resolução
Tema: Ângulos e circunferência
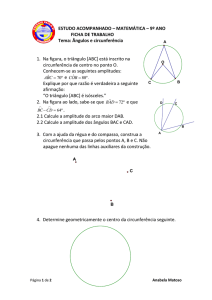
1. O triângulo [ABC] é isósceles porque:
ˆ B  80º então CAˆ B  40º pois CAB é um ângulo inscrito no mesmo arco.
Se CO
Como a soma das amplitudes dos ângulos internos de um triângulo é 180º ,
ACˆB  180º40º70º  ACˆB  70º .
O triângulo [ABC] tem assim dois ângulos com a mesma amplitude e os lados opostos a
esses ângulos são geometricamente iguais.
2. 2.1 A amplitude do arco maior DAB é 360º144º  216º .
2.2 Seja x a amplitude do arco DC e y a amplitude do arco CB.
 x  y  144
 x  x  64  144
2 x  80
 x  40




 y  x  64
 y  x  64
_____
 y  104
Então, como os ângulos inscritos têm metade da amplitude dos arcos
ˆ D  20º e BAˆ C  52º
correspondentes, CA
3. Em primeiro lugar traçam-se duas cordas, por exemplo [AC] e [AB].
Uma vez que a mediatriz de cada uma das cordas contém o centro da circunferência, o
ponto de intersecção das duas mediatrizes é o centro da circunferência (O).
O raio da circunferência é por exemplo OA .
4. Basta traçar duas cordas não paralelas na circunferência e proceder como no exercício
anterior.
ˆ
5. 5.1.1 Uma vez que a recta AD é tangente à circunferência em A, DAO  90º . Como
60º
 30º
ADˆ B  30º , AOˆ B  180º90º30º  AOˆ B  60º .5.1.2 ACˆ B 
2

5.1.3 AB  AOˆ B  60º 5.1.4 A amplitude do arco maior ACB é 360º60º  300º .
5.2.1 O triângulo [AOB] é isósceles pois OA  OB por serem raios da circunferência.
5.2.2 Uma vez que OA  OB e como num triângulo a lados iguais se opõem ângulos
ˆ O  ABˆ O . Como AOˆ B  60º , BAˆ O 
iguais, BA
180º 60º
 60º e ABˆ O  60º .
2
ˆ B  90º pois é um ângulo inscrito numa semi-circunferência.
6.1.1 AG



6.1.2 AOˆ C  AC  40º
6.1.3 BD  AC  40º porque arcos compreendidos
entre cordas paralelas são geometricamente iguais e portanto têm a mesma
amplitude.
ˆ D  180º40º40º  100º
6.1.4 CO
6.2 São geometricamente iguais pois cordas compreendidas entre cordas paralelas são
geometricamente iguais.
6.3 Uma vez que EF é perpendicular a [CD] e contém o centro da circunferência
podemos concluir que é a mediatriz de [CD]. Sendo assim o ponto M pertence à
mediatriz de [CD] e portanto é o ponto médio desse segmento de recta.
6.4.2 Seja x a área do sector circular AOC x
______ 40º
2
  9 ______ 360º
x
  81  40
360
 x  28,3 cm 2
6.4.3 Seja y o comprimento do arco menor AB. Como se trata de uma semicircunferência, y é metade do perímetro da circunferência
y
2 9
 y  28,3 cm .
2
Página 1 de 1
Anabela Matoso