Questão 01)

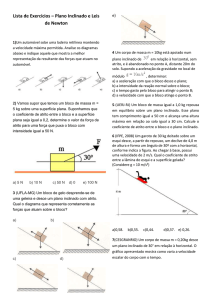
Questão 01)
Um garoto sobre o seu skate desliza livremente numa superfície horizontal, com
velocidade escalar constante de 36 km/h e energia cinética de 2,5 kJ, conforme
ilustra a figura I. Numa segunda situação, esse mesmo garoto (com o seu skate)
encontra-se parado sobre o plano inclinado ilustrado na figura II, segurando-se a
uma corda esticada, presa à parede. Desprezando-se o atrito e considerando-se a
corda e a polia como ideais, a força tensora na corda, na segunda situação, tem
intensidade
a)
b)
c)
d)
e)
5,00 . 102 N
4,00 . 102 N
3,00 . 102 N
2,31 . 102 N
2,31 . 101 N
Questão 02)
Um pequeno bloco de 5,00 kg parte do repouso, no topo do plano inclinado
ilustrado ao lado. O coeficiente de atrito dinâmico entre as superfícies em contato é

d = 0,25 e o módulo de g é 10 m/s2. Realizado o percurso integral, em trajetória
retilínea no plano da figura, o bloco atinge a parede com quantidade de movimento
de intensidade:
a)
b)
c)
d)
e)
4,0 kgm/s
4,9 kgm/s
20,0 kgm/s
24,5 kgm/s
200 kgm/s
Questão 03)
Um catador de recicláveis de massa m sobe uma ladeira puxando seu carrinho. O
coeficiente de atrito estático entre o piso e os seus sapatos é e e o ângulo que a
ladeira forma com a horizontal é . O carrinho, por estar sobre rodas, pode ser
considerado livre de atrito. A maior massa do carrinho com os recicláveis que ele
pode suportar, sem escorregar, é de:
a)
 sen  
m  e
 1
 cos 

b)
 cos  
m  e
 1
 sen  
c) m(e cos – sen)
d) m(e sen – cos)
e)
cos  

m  e 

sen  

Questão 04)
Uma bola desliza inicialmente sobre um plano inclinado (trecho 1), depois, sobre
um plano horizontal (trecho 2) e, finalmente, cai livremente (trecho 3) como mostra
a figura.
1
2
3
Desconsidere as forças de atrito durante todo o movimento.
Considere os módulos das acelerações da bola nos trechos 1, 2, e 3 como sendo a1,
a2 e a3, respectivamente.
Sobre os módulos dessas acelerações nos três trechos do movimento da bola, pode–
se afirmar que:
a) a1 < a2 < a3
b) a1 < a3 e a2 = 0
c) a1 = a2 e a3 = 0
d) a1 = a3 e a2 = 0
Questão 05)
Um corpo escorrega por um plano inclinado, sem a ação de forças dissipativas. A
aceleração da gravidade é de 10 m/s2. Partindo do repouso, ele desce 10m em 2,0 s.
Nessas condições, o ângulo que o plano inclinado forma com a horizontal mede
a) 15°
b) 30°
c) 45°
d) 60°
e) 75°
Questão 06)
Os esquemas abaixo mostram quatro rampas AB, de mesma altura AC e perfis
distintos, fixadas em mesas idênticas, nas quais uma pequena pedra é abandonada,
do ponto A, a partir do repouso.
Após deslizar sem atrito pelas rampas I, II, III e IV, a pedra toca o solo, pela
primeira vez, a uma distância do ponto B respectivamente igual a dI, dII, dIII e dIV.
A relação entre essas distâncias está indicada na seguinte alternativa:
a)
b)
c)
d)
dI > dII = dIII > dIV
dIII > dII > dIV > dI
dII > dIV = dI > dIII
dI = dII = dIII = dIV
Questão 07)
Um bloco escorrega a partir do repouso por um plano inclinado que faz um ângulo
de 45º com a horizontal. Sabendo que durante a queda a aceleração do bloco é de
5,0 m/s2 e considerando g= 10m/s2, podemos dizer que o coeficiente de atrito
cinético entre o bloco e o plano é
a)
b)
c)
d)
e)
0,1
0,2
0,3
0,4
0,5
Questão 08)
Uma pequena caixa está escorregando sobre uma rampa plana, inclinada de um
ângulo  com a horizontal, conforme ilustra a figura. Sua velocidade escalar varia
com o tempo, segundo o gráfico dado. Considerando que o módulo da aceleração
gravitacional local é g = 10 m/s2, sen  = 0,60 e cos  = 0,80, o coeficiente de atrito
cinético entre as superfícies em contato é:
a)
b)
c)
d)
e)
c
= 0,25
 c = 0,50
 c = 0,75
 c = 0,60
 c = 0,80
Questão 09)
Um caminhão-tanque, transportando gasolina, se move no sentido indicado com
aceleração a. Uma pequena bóia b flutua na superfície do líquido como indica a
figura.
A inclinação do liquido no interior do tanque, expressa pela tangente do ângulo , é
igual a:
a) a/g
b) 2(a/g)
c) 3(a/g)
d) 4(a/g)
Questão 10)
Um bloco de massa igual a 2.0 kg é abandonado, sem velocidade inicial, do topo de
um plano inclinado com 5,0 m de altura máxima. Ao longo do plano inclinado, o
movimento ocorre com atritos desprezíveis. Na base do plano inclinado, situa-se um
plano horizontal no qual o bloco desliza ao longo de 10m, ao fim dos quais ele pára,
depois de realizar um movimento uniformemente retardado.
Supondo-se que o módulo da aceleração gravitacional local seja igual a 10m/s²,
calcule:
a) o módulo da velocidade com que o bloco chego à base do plano Inclinado e
b) o módulo da resultante dos forças de oposição que fazem com que o bloco venha
a parar no plano horizontal.
GABARITO:
1) Gab: C
2) Gab: C
3) Gab: B
4) Gab: B
5) Gab: B
6) Gab: D
7) Gab: C
8) Gab: B
9) Gab: A
10) Gab:
a) 10m/s
b) 10N