Tabelas e Gráficos

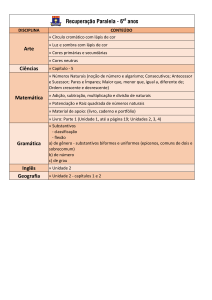
Possibilidades e raciocínio combinatório
Possibilidades são maneiras diferentes de fazer a mesma coisa.
1) Bira está desenhando e construindo pipas. Ele quer que as pipas tenham sempre 2 de suas partes pintadas da
mesma cor. Além disso, as pipas devem ser diferentes umas das outras. Vamos ajudá-lo?
a) Continue desenhando e pintando as outras possibilidades e responda: Qual o número total de possibilidades?
b) Agora descubra todas as possibilidades usando 2 cores diferentes. Desenhe, pinte e escreva o número de
possibilidades.
2) Camila foi à sorveteria e pediu um sorvete com três bolas: morango, chocolate e flocos. De quantas maneiras
diferentes o sorvete pode ser colocado na casquinha?
3) Resolva:
a) Usando os algarismos 2, 4, 6 e 8, escreva todos os números naturais formados por dois algarismos diferentes.
b) Qual é o total de números de 2 algarismo que você escreveu?
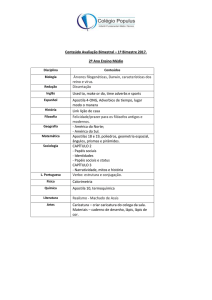
DESAFIO: Descubra todas as outras possibilidades de trocas uma nota de 100 reais uando apenas notas de 50, 10 e
5 reais
a) Complete a tabela.
b) Qual é o total de possibilidades?
R$ 50,00
R$ 10,00
R$ 5,00
2
-
-
1
5
-
1
4
2
1
3
4
Estatística
Qual a sua cor favorita?
A partir de uma pergunta como essa, podemos organizar uma pesquisa de opinião.
As várias respostas obtidas são registradas em uma tabela.
Com a tabela pronta, construímos um gráfico.
Esse modo de organizar dados faz parte de um assunto chamado estatística.
1) Na 3.ª série de Jussara foi feita uma pesquisa sobre o esporte favorito de um grupo de alunos. Observe a tabela e
o gráfico e responda:
a) Qual o esporte mais escolhido?
b) Qual o esporte menos escolhido?
c) Quantos alunos foram pesquisados?
d) Qual é a diferença dos votos entre o futebol e a natação?
e) Quantos votos a mais teve o vôlei em relação ao tênis?
2) A turma de Fabrício vai a pé para a escola. As crianças resolveram fazer um gráfico da distância em quarteirões
das suas casas à escola. Observe o gráfico:
Agora, responda:
a) Quem mora mais longe da escola?
b) Quem mora mais perto da escola?
c) Quem mora a menos de 8 quarteirões da escola?
d) Quem mora mais perto da escola: Sílvia ou Luís?
e) A casa de Paulo fica a quantos quarteirões da escola?
f) Escreva o nome dos alunos em ordem, de acordo com a distância em que eles moram da escola (do mais perto ao
mais longe).
g) Quem mora a mais de 11 quarteirões da escola?
h) Fabrício nada quantos quarteirões a mais que Sílvia para ir à escola?
i) Invente uma pergunta e responda-a.
3) Uma equipe da escola fez uma pesquisa nas classes da 3.ª série: entre os times gaúchos, qual é o seu favorito?
Cada aluno consultou 10 pessoas em classes diferentes e registrou as respostas em gráficos de barra. Veja os
gráficos:
Responda:
a) Qual o time mais votado na turma A? E na C?
b) Qual obteve mais votos na turma B: Grêmio ou Juventude?
c) Quantos foram dados ao Caxias na turma D?
d) Em qual classe Internacional e Juventude tiveram a mesma votação?
e) Em qual das classes o Grêmio obteve mais votos? E menos?
f) Calcule o total de votos recebidos por cada time nas quatro classes.
g) Construa, em papel quadriculado, um gráfico de barras com esses dados (as 4 classes juntas).
Probabilidade
Veja a figura:
Se você girasse a setinha na roleta A, haveria mais chance de ela para no azul ou no vermelho? E na roleta B,
em qual cor é mais provável que ela parasse?
Vamos aprender a resolver problemas para saber qual fato tem maior ou menor chance de ocorrer, ou seja,
qual a probabilidade de ele acontecer.
Podemos expressar essa chance por números. Veja o exemplo:
No seu estojo tem 10 lápis de cor e 2 lápis pretos. Se você retirar um lápis, sem olhar, é mais provável você
pegar um lápis de cor ou um lápis preto? Como há muito mais lápis de cor do que pretos, a chance de pegar um
lápis de cor é maior.
Observe:



Lápis de cor: 10
Lápis pretos: 2
Total de lápis: 10 + 2 = 12
A chance de retirar um lápis de cor, sem olhar, é de 10 em 12, ou seja, 10/12. A chance de retirar um lápis
preto é de 2 em 12, ou seja, 2/12. A esse número chamamos de probabilidade.
1) Coloque numa caixa de sapatos 1 bola vermelha, 2 azuis e 2 amarelas. Tire uma bola sem olhar. Marque a cor
dela na tabela. Devolva a bola na caixa.
Cor
Marcas
Número
Vermelha
Azul
Amarela
a) Faça uma “previsão”: se você repetisse isso 20 vezes, que cor seria a menos tirada?
b) Conferindo sua “previsão”: repita 0 vezes e veja o que ocorreu. Sua “previsão” foi correta?
2) Coloque numa caixa 2 blocos amarelos, 3 azuis e 4 verdes. Agora, responda:
a) Se você retirar um bloco sem olhar, qual tem mais chance de sair? Qual tem menos chance de sair?
b) Qual é o total de blocos na caixa?
c) A probabilidade de o bloco verde sair é de 4 em 9, ou seja, 4/9. Qual é a probabilidade de sair o amarelo? E o
azul?
3) Aninha vai lançar um dado. Responda:
a) Qual é a probabilidade de sair um número par?
b) Qual é a de sair um número ímpar?
c) E a de sair o número 4?
d) E a de sair um número menor que 4?
e) E a de sair um número maior que 4?
f) Há mais probabilidades de Aninha tirar números pares ou ímpares?
g) Qual tem mais probabilidade de sair: o número 4, um número maior que 4 ou um número menor que 4?
Referências Bibliográficas
Dante, Luiz Roberto. Matemática. 2. ed. São Paulo: Ática, 2003, 3ª série