DISPOSITIVOS ELETROMAGNÉTICOS
1) Energia e co-energia magnética
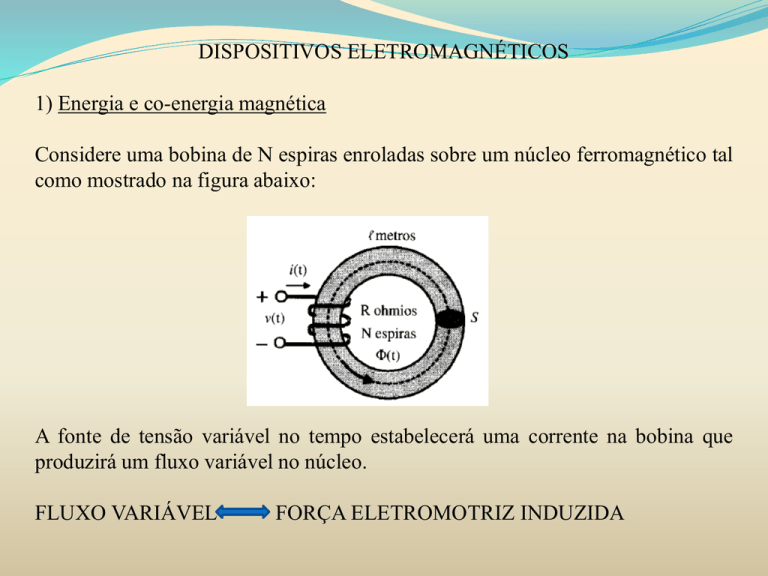
Considere uma bobina de N espiras enroladas sobre um núcleo ferromagnético tal
como mostrado na figura abaixo:
A fonte de tensão variável no tempo estabelecerá uma corrente na bobina que
produzirá um fluxo variável no núcleo.
FLUXO VARIÁVEL
FORÇA ELETROMOTRIZ INDUZIDA
DISPOSITIVOS ELETROMAGNÉTICOS
A fem será induzida em cada espira do enrolamento produzindo uma fem total
que pode ser considerada como uma elevação de tensão no sentido do fluxo de
corrente.
d
(1)
dt
Ou como uma queda de tensão no sentido da corrente denominada de força
contra-eletromotriz (fcem) cuja magnitude é:
e N
d
e N
(2)
dt
DISPOSITIVOS ELETROMAGNÉTICOS
As formas acima expressam a mesma lei (Faraday-Lenz).
Na parte superior da figura (a) observa-se que a polaridade da fem induzida é tal
que produz uma corrente (se a espira estiver em curto-circuito) de tal maneira que
o fluxo induzido (produzido por esta) está no mesmo sentido do fluxo indutor
Φ(t) e é por isso que se faz necessário incluir o sinal (-) na expressão da fem.
DISPOSITIVOS ELETROMAGNÉTICOS
O sinal (-) na fem serve para atender a lei de Lenz de oposição a variação de
fluxo magnético.
No caso da figura inferior se observa que a polaridade da fem induzida é
contrária a do caso anterior. Nesta situação a corrente induzida na espira cujo o
fluxo induzido se opõe ao fluxo principal Φ(t). É por esse motivo que não é
necessário incluir o sinal (-) na fem, já que com a polaridade associada se obtém
um fluxo induzido que é contrário ao fluxo principal.
Aplicando a lei de Kirchhoff no circuito resulta em:
d
v Ri N
(3)
dt
vidt Ri 2 dt Nid
A equação (4) pode ser escrita de outro modo:
dWe dWR dWm
DISPOSITIVOS ELETROMAGNÉTICOS
dWe = diferencial de energia de entrada
dWR = diferencial de energia dissipada na resistência R
dWm = diferencial de energia armazenada no campo magnético
A equação 5 representa o balanço energético do circuito ou simplesmente a lei da
conservação da energia.
O diferencial de energia magnética pode ser escrito como:
dWm Nid
dWm Fmm d
Supondo que no instante t=0 o fluxo no núcleo é nulo e a corrente seja nula, a
energia magnética total fornecida pela fonte é:
Wm Fmm d
0
DISPOSITIVOS ELETROMAGNÉTICOS
CO-ENERGIA
A co-energia pode ser definida da seguinte forma:
Wm'
Fmm
dF
mm
0
A co-energia não possui significado físico direto, porém tem grande aplicação no
cálculo de forças nos dispositivos eletromagnéticos.
DISPOSITIVOS ELETROMAGNÉTICOS
CO-ENERGIA
A soma da energia mais a da co-energia magnética equivale a área do retângulo
F.Φ.
Sabendo-se que:
B A d A dB
F Hl dF ldH
B
0
0
Wm Fd vol HdB
A densidade de energia pode ser calculada por:
B
W
w m m HdB
vol 0
DISPOSITIVOS ELETROMAGNÉTICOS
Sabendo-se que:
F
H
H
0
0
0
Wm' dF B AldH vol BdH
A densidade de co-energia magnética é dada por:
w 'm
Wm'
vol
H
BdH
0
Quando a curva de magnetização é considerada linear, os resultados anteriores
dão lugar a expressões mais simples.
Nesse caso o valor da energia e o valor da co-energia são iguais e dado por:
1
1
1 F2
2
Wm W F R
2
2
2R
'
m
DISPOSITIVOS ELETROMAGNÉTICOS
De mesmo modo as densidades de energia e de co-energia são:
1
1 B2 1
w m w m HB
H 2
2
2 2
'
Sabe-se também que a indutância pode se calculada através de:
LN
i
E que:
F R
N2
2
2
LN LN
N
i
Ni
F
R
E a energia e a co-energia dadas por:
2
1
F
1
Wm Wm' L 2 Li 2
2 N
2
DISPOSITIVOS ELETROMAGNÉTICOS
PERDAS DE ENERGIA EM NÚCLEOS
FERROMAGNÉTICOS
Existem dois tipos de perdas de energia associada em núcleos ferromagnéticos:
característica de histerese do material (perdas por histerese) e correntes induzidas
no núcleo (perdas por correntes parasitas).
Perdas por histerese
DISPOSITIVOS ELETROMAGNÉTICOS
Se considerarmos que a indução no núcleo varia desde –Br até Bm seguindo o
trecho da curva (abc) ocorrerá um aumento da indução no núcleo o que
corresponde a uma energia absorvida pelo campo magnético e armazenada
durante parte do ciclo.
Wac vol
Bm
HdB vol w
1
Br
A integral w1 representa a área da superfície abcdea.
Considerando que a indução é reduzida de Bm(ponto c) até Br (ponto e ) seguindo
o trecho (ce) da curva de histerese, então resultará em uma energia devolvida a
rede durante parte do ciclo porque é negativa e cujo valor é dado por:
Wce vol
Br
HdB vol w
2
Bm
A área cdec representa a densidade de energia correspondente que é valor w2 na
fórmula acima.
DISPOSITIVOS ELETROMAGNÉTICOS
A área cdec representa a densidade de energia correspondente que é valor w2 na
fórmula abaixo.
Wce vol
Br
HdB vol w
2
Bm
Quando se submete o núcleo a uma indução crescente entre –Br e Bm seguindo o
caminho abc e logo a outra indução entre decrescente entre Bm e Br seguindo o
caminho ce, a superfície resultante <<abcea>> representará a densidade de
energia absorvida pelo núcleo ferromagnético com a excitação cíclica e que não é
devolvida a rede, sendo esta dissipada no núcleo em forma de calor.
DISPOSITIVOS ELETROMAGNÉTICOS
Circuitos magnéticos
excitados por corrente alternada
A Lei de Hopkinson expressa pela equação:
F
R
Em que:
Φ – fluxo magnético
F- força magnetomotriz
R – Relutância magnética
Se considerarmos o circuito magnético da figura abaixo:
DISPOSITIVOS ELETROMAGNÉTICOS
Se considerarmos o circuito magnético da figura abaixo:
A bobina acima possui resistência (Rb). Ao aplicar uma tensão contínua na
bobina será produzido de acordo com a lei de Ohm uma corrente dada por:
I
V
Rb
Essa corrente produzirá uma força magnetomotriz e que dependendo do valor da
relutância magnética determinará um fluxo resultante.
DISPOSITIVOS ELETROMAGNÉTICOS
Verifique abaixo a sequência:
Observe que quando uma excitação cc é aplicada em uma bobina, a corrente é
função da tensão aplicada, porém é absolutamente da natureza e características
magnéticas do material que constitui o núcleo.
Suponha agora que a bobina é alimentada por uma tensão senoidal:
v(t) 2V cos(t)
Circulará uma corrente i(t) que provocará um fluxo Φ(t) no núcleo. Este fluxo
variável produzirá uma fem induzida na bobina de tal forma que ao se aplicar a
lei de Kirchhoff resulta em:
d
v(t) Ri(t) N
dt
Supondo que a queda de tensão na bobina seja pequena quando comparada com a
fem induzida, então a equação pode ser escrita como:
v(t) N
d
dt
De onde se tem o valor do fluxo magnético:
d
v(t) N
dt
1
2
(t) v(t)dt
Vsen(t)
N
A constante de integração é nula sempre que se considera que em t=0 não existe
magnetismo residual no núcleo. A equação pode ser escrita na maneira clássica
como:
1
2
v(t)dt
Vsen(t)
N
(t) max sen(t) max cos(t 90o )
(t)
E o fluxo máximo vale:
max
2V
N
Então:
V
2
fNmax 4, 44fNmax
2
É importante destacar aqui que a tensão aplicada e a frequencia impõem o valor
do fluxo no núcleo e que com o valor da relutância magnética do núcleo terá uma
corrente absorvida pela bobina.
OBS: Quando uma bobina é alimentada por uma tensão c.a, o fluxo é função
direta do módulo e da frequência da tensão aplicada, mas é independente da
natureza e das características magnéticas do material que constitui o núcleo.
Se considerarmos que houve um aumento da relutância magnética ( por ter
acrescentado um entreferro) não haverá nenhuma mudança do valor do fluxo,
entretanto a bobina absorverá mais corrente da rede para manter o fluxo constante
no valor imposto pela tensão aplicada.
Circuito equivalente de uma bobina com núcleo de ferro
alimentada por uma tensão c.a
Como demonstramos anteriormente, o fluxo no núcleo é independente da
natureza do material magnético, logo os efeitos da saturação e da histerese terão
influência na corrente absorvida.
Consideraremos incialmente o circuito magnético linear, o que vale dizer que o
sistema possui permeabilidade constante.
Para determinar o circuito equivalente de uma bobina com núcleo de ferro, é
preciso considerar duas situações:
a)
O núcleo não apresenta perdas no ferro
b) O núcleo apresenta perdas no ferro
Se considerarmos que o núcleo magnético não apresenta perdas e supomos que a
resistência pode ser desprezada, a potência absorvida pela bobina é nula.
De acordo com a fórmula abaixo:
Ni
F Ni exc
exc A
l
R
l
A
Sabendo-se que:
vN
d
dt
Supondo permeabilidade constante:
d
d Ni
vN
exc A
dt
dt
l
N 2 A di exc
v
l
dt
O diagrama fasorial é mostrado abaixo:
Comparando com a tensão de uma bobina de coeficiente de auto-indução L
conduzindo uma corrente iiex.
vL
di exc
dt
Isto indica que L pode ser expressado por:
N 2 A
L
l
Conclui-se que o circuito equivalente de uma bobina de ferro pode ser
representado por uma auto-indutância.
Vamos apresentar agora o caso em que o núcleo magnético apresenta perdas:
No caso em que o núcleo magnético apresenta perdas, a corrente de excitação
fará um ângulo de 90º com a tensão e a potência ativa absorvida da rede deve
compensar as perdas.
Se denominarmos φv o ângulo que é formado entre a tensão e corrente, e que Pfe
são as perdas no ferro, então:
Pfe VIex cos(v )
Pode-se observar que a corrente de excitação possui duas componentes: uma
componente de perdas no ferro e a outra denominada de corrente magnetizante.
Elas podem ser calculadas por:
Ife Iex cos(v )
I Iex sen(v )
I exc I fe I
O circuito equivalente para o núcleo considerado com perdas e com
permeabilidade constante é mostrado abaixo. A potência absorvida pode ser
representada por uma resistência, denominada de resistência de perdas e a
corrente magnetizante defasada de 90º em relação à tensão aplicada circular por
uma reatância denominada de reatância magnetizante.
R
V
V
.................X
Ife
I
Corrente de excitação em uma bobina
com núcleo de ferro alimentada com c.a
Anteriormente, a determinação da corrente de excitação foi obtida supondo um
circuito magnético linear de permeabilidade constante o que se permitiu obter
expressões simples que relacionam tensão e corrente ou fluxo e corrente.
A linearidade implica diretamente que se a tensão aplicada for senoidal a corrente
e o fluxo são também senoidais.
Entretanto, a curva de magnetização dos materiais magnéticos é não-linear e
ponto de trabalho normal das máquinas elétricas está perto do joelho da curva, o
qual exerce grande influência na forma da corrente de excitação deixando de ser
senoidal e para sua determinação é necessário a utilização de ferramenta gráfica,
por ser impossível utilizar técnicas analíticas.
Para determinação da forma de onda da corrente de excitação é necessário
considerar dois casos:
1) Núcleo sem perdas
2) Núcleo com perdas
Corrente de excitação em uma bobina
com núcleo de ferro alimentada com c.a
1) Núcleo sem perdas
A relação neste caso entre fluxo Φ e corrente de excitação Iexc se obtém
graficamente a partir da curva de magnetização do material, onde em vez de
empregar a indução no eixo y, se utiliza o fluxo Φ=B x A, e no eixo das abcissas
se utiliza H= Niexc / l.
Observe a figura no slide seguinte:
A curva de magnetização do material consiste no gráfico Φ=f(iiexc ).
Na outra figura observa-se a forma da onda do fluxo e da tensão.
Observa-se que a forma da onda da corrente é não-senoidal e pode ser
decomposta em serie de Fourier demonstrando ser composta por harmônicos
ímpares.
2) Núcleo com perdas
CONVERSÃO DE ENERGIA EM SISTEMAS
MAGNÉTICOS COM MOVIMENTO DE TRANSLAÇÃO
Anteriormente (link) ficou definido que um campo magnético armazena energia.
Por outro lado, o campo magnético exerce forças mecânicas nas estruturas ou
partes das estruturas associadas com ele.
Estas propriedades fazem com que o campo magnético seja utilizado como meio
de ligação entre as partes elétricas e mecânicas de muitos dispositivos
eletromecânicos e em particular as máquinas elétricas que dispositivos que
convertem energia.
Considere o seguinte sistema magnético dotado de movimento de translação:
Quando circula uma corrente pela bobina de excitação, é estabelecido um fluxo
magnético no núcleo que provoca uma força de atração sobre a armadura móvel,
o reduz o entreferro central com a redução da relutância do circuito magnético e
com a consequente e da variação da energia magnética armazenada.
Se a armadura móvel se desloca para a esquerda desde uma posição inicial x=x1
para uma posição final x2 = x-dx, o princípio da conservação da energia aplicado
ao sistema estabelece a seguinte equação:
dWe dWm dWmec dWp
dWe dWm dWmec dWp
Em que:
dWe - variação da energia elétrica absorvida
dWm - variação da energia magnética armazenada
dWmec - variação da energia mecânica devida ao movimento da armadura móvel
dWp - variação da energia perdida
Essa equação corresponde a lei da conservação da energia aplicada em um
sistema motor, ou seja, uma transformação da energia elétrica em mecânica.
Considerando que as perdas sejam desprezíveis:
Essas perdas correspondem a:
Perdas por efeito joule na bobina, perdas no ferro do núcleo magnético (histerese
e correntes parasitas) ; perdas mecânicas no deslocamento da armadura móvel.
Desprezando as perdas resulta que:
dWe dWm dWmec
Desprezando as perdas resulta que:
dWe dWm dWmec
Na figura do slide anterior existem duas curvas de magnetização, uma para cada
posição da armadura móvel, ou seja, a curva de magnetização depende da
distância (x).
Se considerarmos um fluxo constante definido por Φ1 , para a posição inicial x1 =
x, necessita-se de uma força magnetomotriz maior.
Se o fluxo for constante, a menor relutância corresponde a menor fmm. Ao
considerar uma força magnetmotriz constante, o fluxo é tanto maior quanto
menor for a relutância do circuito magnético (menor entreferro).
Se supormos uma situação inicial com entreferro x1 = x e um fluxo no núcleo
igual a Φ1 a energia magnética armazenada será expressa por oaco. Quando se
desloca a armadura móvel, a posição muda de x1 a x2 .
A localização do novo ponto de trabalho (novo estado) depende de como é
efetuado o deslocamento.
MOVIMENTO SE REALIZA
COM FLUXO CONSTANTE
Essa situação é obtida ajustando a corrente durante o movimento ou considerando
que o deslocamento do núcleo é suficientemente rápida para que não haja tempo
de variar o fluxo durante o deslocamento.
Nesse caso, a energia elétrica absorvida da rede será nula.
dWe vidt N
d
idt Nid
dt
Como não há variação do fluxo durante o movimento isto indica então que dWe =
0. Então:
dWe dWm dWmec
dWe 0
0 dWm dWmec
dWmec dWm
A fórmula indica que o trabalho mecânico se realiza apenas devido a redução da
energia magnética armazenada.
Se o fluxo permanece constante durante o movimento da armadura móvel, o novo
estado de equilíbrio corresponderá ao ponto b da figura abaixo:
Para o qual a energia magnética armazenada neste estado final é expressa pela
área obco. Prova-se então que ocorre uma redução da energia magnética durante
a translação expressa pela área oabo. Essa variação ocorrida na energia magnética
será igual ao trabalho mecânico realizado.
Se a força de atração for designada por f, então o trabalho mecânico produzido
dado por:
dWe [f dx]
W
f e
x cte
OBS: A FORÇA MECÂNICA SOBRE A ARMADURA MÓVEL TENDE A
REDUZIR A ENERGIA MAGNÉTICA ARMAZENADA NO CIRCUITO
MAGNÉTICO, E ISTO OCORRE QUANDO SE REDUZ O ENTREFERRO E
CONSEQUENTEMENTE O SENTIDO DA FORÇA EXERCIDA SOBRE A
ARMADURA MÓVEL É SEMPRE DE ATRAÇÃO.
Se as curvas de magnetização da figura [ link] forem retas, o que ocorre na
prática quando os entreferros são grandes, a expressão da energia magnética
armazenada é:
1
We R 2
2
dR
1
f 2
dx
2
A força sobre a armadura móvel ocorrerá no sentido da redução da relutância do
circuito magnético.
MOVIMENTO SE REALIZA COM
CORRENTE CONSTANTE
Esta situação é estabelecida quando o movimento da armadura móvel é
suficientemente lento. Verifique a figura abaixo:
A posição inicial corresponde ao ponto (a), cujo fluxo é Φ1 e o novo estado de
equilíbrio caso a corrente se matenha constante corresponderá ao ponto (e)., no
qual o fluxo tem valor Φ2 .
Ao existir uma variação do fluxo no sistema, existirá consequentemente uma
variação de energia elétrica de entrada na bobina durante a transição de um
estado para outro.
Aplicando o princípio da conservação da energia resulta que:
dWe dWm dWmec Nid Fd
Sabe-se também que:
Wm Wm' F
Diferenciando a equação anterior resulta em:
Wm Wm' F
dWm dWm' Fd dF
Fazendo as devidas substituições resulta em:
dWm dWmec Nid Fd
dWm dWm' Fd dF dWm Fd dF dWm'
Fd dF dWm' dWmec Fd dF
Fazendo as simplificações e levando em conta que dF=0 no deslocamento (pois a
força magnetomotriz é constante), resulta em:
Fd dF dWm' dWmec Fd dF
dF 0
dWmec dWm'
ISTO INDICA QUE O TRABALHO MECÂNICO REALIZADO SE DÁ EM
FUNÇÃO
DO
AUMENTO
DA
CO-ENERGIA
MAGNÉTICA
ARMAZENADA.
Sabendo-se que a co-energia inicial é dada pela área (odao) e a co-energia final é
dada pela área (odeo).
A variação da co-energia é a diferença entre a co-energia final e a co-energia
'
inicial dada pela área hachurada e que segundo a fórmula dWmec dWm define
também o trabalho desenvolvido no movimento.
A expressão da força em função da co-energia é dada então por:
Wm'
f
x
Considerando o sistema linear, então:
1 F2
W
2R
1 2 d 1 1 2 dP
f F
F
2 dx R 2 dx
'
m
Em que P é denominada de permeância que é o inverso da relutância.
EXERCÍCIOS
CONVERSÃO DE ENERGIA EM SISTEMAS MAGNÉTICOS
COM MOVIMENTO DE ROTAÇÃO
MÁQUINAS ELÉTRICAS ROTATIVAS
Em geral as máquinas elétricas são dispositivos eletromagnéticos dotados de
movimento de rotação. Para analisar a conversão de energia nestes sistemas,
vamos considerar duas situações que ocorrem frequentemente na prática.
A primeira em que o sistema dispões de uma fonte de alimentação apenas e a
segunda em que o sistema magnético dispões de várias fontes de alimentação,
normalmente duas.
1) Sistemas magnéticos de rotação alimentados com uma fonte apenas
1) Sistemas magnéticos de rotação alimentados com uma fonte apenas
De maneira semelhante ao movimento de translação, se considerarmos que a
rotação ocorre com fluxo constante, a equação demonstrada para o movimento de
translação é válida aqui também.
A equação que exprime o princípio da conservação da energia é dada por:
dWmec dWm
Sabendo-se que o primeiro membro está relacionado com a energia mecânica,
então:
dWmec T d
De onde deduz-se que:
W
T m
cte
Se o sistema é considerado linear, o equivale a supor que a única relutância que
existente corresponde a do entreferro, então:
1
Wm R 2
2
Substituindo na fórmula do torque resulta em:
1
dR
T 2
2
d
Substituindo na fórmula do torque resulta em:
1 2 dR
T
2
d
A FÓRMULA INDICA QUE O CONJUGADO ATUA NO SENTIDO DE
REDUZIR A RELUTÂNCIA ENTRE O ESTATOR E O ROTOR, OU SEJA,
EXISTE UMA TENDÊNCIA DE ALINHAMENTO DO EIXO MAGNÉTICO
DO ROTOR COM O EIXO MAGNÉTICO DO ESTATOR.
Se o movimento é realizado com corrente constante (força magnetomotriz
constante) , as equações se transformam em:
1 dP
T F2
2 d
1 2 dL
T i
2 d
É fácil demonstrar que tanto a relutância quanto a permeância e a indutância é
função do ângulo θ que forma o estator com o rotor.
De maneira semelhante, a indutância será mínima quando o eixo do rotor forme
um ângulo de 90º (eixo em quadratura) com o eixo do estator. Denominando Lq
a esse valor de indutância, segue que:
L( 90o ) L 270o L q
A figura seguinte mostra a variação da indutância com o ângulo θ que varia entre
Ld e Lq seguindo uma lei senoidal.
A indutância pode ser dada matematicamente por uma lei senoidal:
L L1 L 2 cos 2
Em θ=0, estabelece que:
L 0 L1 L 2 L d
Em Em θ=90o, estabelece que:
L 90o L1 L 2 L q
As indutâncias L1 e L2 são funções das indutâncias Ld e Lq .
Ld Lq
L1
2
L2
Ld Lq
2
Substituindo as expressões na fórmula do torque resulta em:
1 dL
T i2
2 d
L1
Ld Lq
2
L2
Ld Lq
2
1 2 dL 1 2 d
T i
i
L1 L 2 cos(2)
2 d 2 d
O torque será igual a:
T i L 2sen(2) i (
2
2
Ld Lq
2
)sen(2)
Se Ld = Lq não ocorrerá nenhum torque. Isto ocorre quando o entreferro é
constante, ou seja, rotor do tipo cilíndrico.
Se considerarmos que a corrente de alimentação é constante (tipo cc) e supões
que o rotor se desloca da posição horizontal de um ângulo θ em direção contrária
ao ponteiro do relógio, aparecerá um conjugado restaurador orientado no sentido
dos ponteiros do relógio.
Em outras palavras: se a corrente for constante o conjugado exercido sobre o
rotor não é unidirecional e está orientado no sentido contrário ao qual o rotor
tende a se mover.
O rotor ficará estacionário em sua posição horizontal (mínima relutância).
Suponha agora que o rotor se move (acionado por um motor externo) a uma
velocidade ωm ; então a posição do rotor é dada por:
m (t)
Se nesta situação, o estator for alimentado por uma corrente senoidal:
i I m cos(t)
Então de acordo com T i L 2sen(2) i (
um torque.
2
2
Ld Lq
T i 2 L 2sen(2) I m2 cos 2 (t)L 2sen2(m t )
2
)sen(2)
será produzido
Levando em conta que:
T i 2 L 2sen(2) I m2 cos 2 (t)L 2sen2(m t )
E que:
1 cos(2t)
cos (t)
2
Substituindo na expressão do torque resulta em:
2
T i 2 L 2sen(2) I m2 cos 2 (t)L 2sen2(m t )
1
T I 2m L 2sen2(t )(1 cos 2t)
2
E sabendo-se que a identidade trigonométrica:
1
sen(a)cos(b) sen(a b) sen(a b)
2
Resultando finalmente:
1
1
1
T I 2m L 2 sen2(m t ) sen[2(m )t ] sen[2(m )t ]
2
2
2
Deve-se observar que o conjugado médio será nulo para velocidades ωm ≠ ω.
Se o rotor gira velocidade ω, (ωm = ω) denominada de velocidade de sincronismo
o conjugado médio é dado por:
2
1
12
T
Td(
t)
I m L 2sen(2)
2 0
4
Este é o princípio que se baseia os motores de relutância. O motor tende a manter
o sentido de rotação mesmo quando é desligado o motor primário.
O ângulo δ é denominado de ângulo de torque.
O ângulo δ é denominado de ângulo de torque.
Para ângulo δ<0, o conjugado médio é positivo o que significa que este
conjugado atua no sentido de rotação da máquina que atua como motor.
Se considerarmos que o motor é ideal (sem perdas) e que não existe conjugado
resistente, então a máquina girará inicialmente com ângulo de torque igual a zero,
e girará neste caso uma carga mecânica então se faz necessário que a máqiuna
produza um conjugado motor.
Como na situação anterior o conjugado motor é nulo, então será produzido um
regime dinâmico em que se reduzirá a velocidade e como resultado disto o
ângulo de torque começará a tomar valores negativos e desenvolverá um
conjugado motor que equilibrará o conjugado resistente e a máquina voltará a
girar na velocidade de sincronismo.
À medida que o conjugado motor aumenta, a ângulo de torque ficará cada vez
mais negativo chegando ao valor onde será desenvolvido torque máximo. Se o
conjugado resistente for maior que este, a máquina sairá do sincronismo e
acabará parando.
A zona estável para operação motora é compreendida entre 0 e – pi/4 e que nesta
zona, à medida que aumenta o conjugado resistente também aumenta o
conjugado motor, pois o ângulo de torque se torna cada vez maior.
Se δ > 0, então o conjugado desenvolvido será negativo de maneira que este atua
em sentido oposto a rotação da máquina e trabalha então como gerador.
O dispositivo mecânico conectado a ele deve fornecer conjugado e potência
mecânica ao rotor. Existe um fluxo de potência elétrica da máquina para a
rede.
A aplicação mais conhecida dos motores de relutância está nos relógios
elétricos e como não produzem torque de partida, se incia a rotação
fornecendo um impulso mecânico no rotor acima da velocidade de
sincronismo, de tal maneira que se alcança um estável ao passar pela
velocidade de sincronismo, mantendo esta velocidade.
SISTEMAS MAGNÉTICOS DE ROTAÇÃO
ALIMENTADOS POR DUAS FONTES
Estes sistemas são os que normalmente são encontrados nas máquinas
elétricas convencionais.
Considerando o sistema magnético linear e relembrando da teoria de
circuitos acoplados, os fluxos magnéticos totais ψ1 e ψ2 que atravessam
ambos enrolamentos:
1 L11i1 L12i 2 N11
2 L 21i1 L 22i 2 N 2 2
Na forma matricial se escreve:
1 L11 L12 i1
L
i
L
22 2
2 21
L11 – representa o coeficiente de auto-indução do enrolamento 1
L22 – é o correspondente do enrolamento 2
A energia magnética total armazenada (igual a co-energia no caso de
sistema linear) é encontrada para cada um dos enrolamentos:
1
1
1
1
Wm Wm' F11 F2 2 i11 i 2 2
2
2
2
2
Considerando que:
1 L11i1 L12i 2 N11
2 L21i1 L22i 2 N 22
Resultando em:
1
1
Wm Wm' L11i12 L 22i 22 L12i1i 2
2
2
Sabendo-se que:
Wm'
T
icte
Sabendo-se que:
Wm'
T
icte
1
1
Wm Wm' L11i12 L22i 22 L12i1i 2
2
2
Os dois primeiros termos representam conjugado de relutância devido as
indutâncias próprias de cada enrolamento . E o terceiro termo na soma
representa o conjugado que se obtém quando varia a indutância mútua entre
ambos enrolamentos
Wm'
T
icte
1
1
'
2
Wm Wm L11i1 L 22i 22 L12i1i 2
2
2
dL12
1 2 dL11 1 2 dL 22
T i1
i2
i1i 2
2 d 2 d
d
De acordo com o que já foi desenvolvido, as indutâncias próprias dos dois
enrolamentos são calculadas da seguinte forma:
L11 La L b cos 2
L 22 L c L d cos 2
Enquanto a indutância mútua dependerá do ângulo formado entre os eixos
magnéticos do rotor e do estator.
L12 L m cos
Tendo em vista a definição de indutância mútua que corresponde ao fluxo
que chega em um enrolamento produzido pelo outro enrolamento.
Ocorre que quando os eixos estão alinhados todo fluxo produzido
atravessará o outro e quando eles formam 90º não haverá fluxo deixando um
enrolamento e atravessando o outro.
OBS: EM GERAL PARA UMA POSIÇÃO ARBITRÁRIA DEVERÁ SER
APLICADA A EQUAÇÃO
SEJA QUAISQUER
L12 Lm cos
DISPOSÍÇÕES MAGNÉTICAS DO ESTATOR E DO ROTOR.
ISTO NÃO OCORRE COM AS EXPRESSÕES
L11 La Lb cos 2 E L22 Lc Ld cos 2 JÁ QUE AS INDUTÂNCIAS
PRÓPRIAS DEPENDERÃO DAS SIMETRIAS MAGNÉTICAS DAS
ESTRUTURAS DO ESTATOR E DO ROTOR.
POR EXEMPLO, SE AMBAS SÃO CILÍNDRICAS, L11 e L22 SERÃO
CONSTANTES E NÃO DEPENDERÁ DE θ PORQUE AO GIRAR O
ROTOR NENHUM DOS ENROLAMENTOS “SENTIRÁ”NENHUMA
VARIAÇÃO DA RELUTÂNCIA.
SE O ESTATOR POSSUI POLOS MAGNÉTICOS SALIENTES E O
ROTOR É CILÍNDRICO, ENTÃO L11 SERÁ CONSTANTE E L22 SERÁ
CALCULADA POR:
L22 Lc Ld cos 2
SE O ESTATOR FOR CILÍNDRICO E O ROTOR POSSUI POLOS
SALIENTES, ENTÃO L22 SERÁ CONSTANTE E L11 TEM A FORMA
INDICADA NA FÓRMULA:
L11 La Lb cos 2
No caso em que relacionaremos a tensão aplicada com a corrente em cada
enrolamento, aplicaremos segunda lei de Kirchhoff a cada enrolamento:
d1
d
R1i1 (L11i1 L12i 2 )
dt
dt
d 2
d
v 2 R 2i 2
R 2i 2 (L 21i 2 L 22i 2 )
dt
dt
v1 R1 0 L11 L12 i1
v 0 R L
i
L
2
22 2
2
21
v1 R1i1











