CAP-3.2

Teoria da Demanda
e Oferta
Parte 2
Economia Pesqueira I
Prof. Rogério César, Ph.D.
Equilíbrio de Mercado

Conceito:

É o resultado da interação entre as forças de oferta e
demanda que são determinadas pelo processo de
negociação entre produtores (vendedores) e
consumidores.

Em equilíbrio, o preço satisfaz tanto ao consumidor quanto
ao produtor de tal forma que a quantidade demandada é
igual a quantidade ofertada.
Qd = Qs
Equilíbrio de Mercado
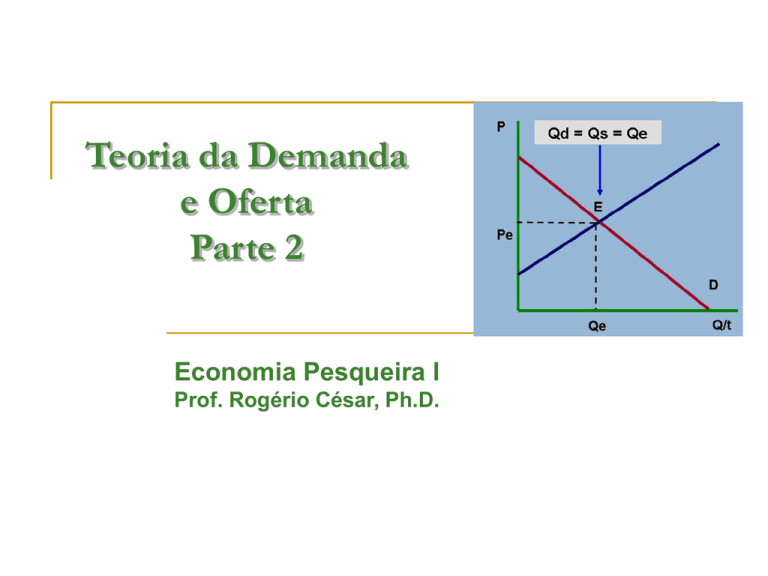
P
Qd = Qs = Qe
S
Ponto de Equilíbrio (E): é o ponto de
intersecção entre D e S.
Preço de Equilíbrio (Pe): é o preço de
mercado que faz com que a quantidade
demandada seja igual a quantidade
ofertada.
E
Pe
D
Qe
Q/t
Quantidade de Equilíbrio (Qe): é a
quantidade ofertada e demandada do
bem, ao preço de equilíbrio de mercado,
que satisfaz aos interesses dos
produtores e consumidores.
Determinação matemática do ponto de
equilíbrio

O preço e a quantidade de equilíbrio são determinados igualandose as quantidades demandadas e ofertadas, como apresentadas no
exercício a seguir.
EXEMPLO
Dadas as funções de demanda e oferta,
determine o preço e quantidade de equilíbrio:
Qd = 100 – 2,5 P
Qs = 50 + 1,5 P
1) Fazer Qd = Qs para encontrar Pe:
100 – 2,5 P = 50 + 1,5 P
- 2,5 P – 1,5 P = 50 – 100
(-2,5 – 1,5) P = - 50
P = - 50 / - 4
P = 12,5 = Pe
2) Substitua Pe em Qd ou Qs para
determinar Qe:
Qe = 100 – 2,5(12,5)
= 50 + 1,5(12,5)
= 68,75
Portanto, temos o ponto de equilíbrio dado
por:
Qe = 68,75
Pe = 12,5
Representação gráfica
Para Q = 0, temos:
0 = 100 – 2,5 P
P
P = - 100 / -2,5 = 40
Qd = Qs = Qe
S
40
Para P = 0, temos:
E
Q = 100 – 2,5(0)
Q = 100
12,5
Para P=0, temos:
Q = 50 + 1,5(0)
D
50
68,75
100
Q/t
Desequilíbrio de Mercado
Conceito:


Desequilíbrio de mercado ocorre quando o
preço praticado no mercado é diferente do preço
de equilíbrio.
Situações de desequilíbrio:



Escassez de oferta
Excesso de oferta.
Escassez de Oferta

Ocorre quando a
quantidade que os
consumidores
desejam demandar
excede a quantidade
que os produtores
desejam ofertar.
P
S
E

Relações de preços e
quantidades:
Pe
P’
A
P’ < Pe
B
D
Q
Qd > Qs
Qs
Q = Qs – Qd < 0
Qe
Qd
Q/t
Excesso de Oferta


Ocorre quando a
quantidade que os
produtores querem
ofertar excede a
quantidade que os
consumidores
querem demandar.
Relações de preços e
quantidades:
P
S
A
B
P’
Pe
E
P’ > Pe
D
Q
Qs > Qd
Qd
Q = Qs – Qd > 0
Qe
Qs
Q/t
Mudanças no Preço de Equilíbrio
Introdução:


No mercado competitivo, ou seja, onde existem
muitos compradores e vendedores, o preço de
desequilíbrio é uma situação instável.

Quando há uma mudança na demanda ou na
oferta, o mecanismo de preços vai operar no
sentido de mover o preço e quantidade para um
novo ponto de equilíbrio.
Mudança na Demanda
Aumento da demanda
resulta em:




Deslocamento da
demanda para
direita
P
P1
Aumento no Pe
Aumento na Qe
E1
S
E0
P0
D1
D0
Q0
Q1
Q/t
Mudança na Demanda
Diminuição da
demanda resulta em:


Deslocamento da
demanda para
esquerda

Diminuição no Pe

Diminuição na Qe
P
S
E0
P0
E1
P1
D0
D1
Q1
Q0
Q/t
Mudança na Oferta
Aumento da oferta
resulta em:


P
S0
Deslocamento da
oferta para direita
S1


Diminuição no Pe
Aumento na Qe
E0
P0
E1
P1
D
Q0
Q1
Q/t
Mudança na Oferta
P
S1
Diminuição da oferta
resulta em:

S0
E1
Deslocamento da
oferta para
esquerda
P1

Aumento no Pe
P0

Diminuição na Qe

E0
D
Q1
Q0
Q/t
Mudança nas Curvas de Oferta e
Demanda
P

Quando ambas as
curvas se deslocam
simultaneamente
S0
Aumento da demanda
E0
+
P0
Aumento da oferta
P1
E1

D0 D1
Diminuição no Pe
Diminuição na Qe
S1
Q0
Q1 Q/t
Mudança nas Curvas de Oferta e
Demanda
P
E1
Aumento da demanda
P1
S1
S0
+
Diminuição da oferta

E0
P0
D1
Aumento no Pe
Aumento na Qe
D0
Q0
Q1
Q/t
Mudança nas Curvas de Oferta e
Demanda
P
Diminuição da demanda
S0
+
S1
Aumento da oferta

E0
P0
Diminuição no Pe
Diminuição na Qe
P1
E1
Q1 Q0
D0
D1
Q/t
Mudança nas Curvas de Oferta e
Demanda
P
S1
Diminuição da demanda
S0
+
E1
Diminuição da oferta
P1

P0
E0
Aumento no Pe
Diminuição na Qe
D0
D1
Q1
Q0
Q/t
Exercício:
Dadas as equações de demanda e oferta para o mercado de tilápia:
Qd = 10 – 3 P + 1,5 I
Qs = - 5 + 5 P – 0,5 T
Determine o ponto de equilíbrio para o mercado de tilápia quando:
Situação inicial: I0 = 100 e T0 = 50
Situação final: I1 = 200 e T1 = 30
Equações Iniciais:
Qd = 10 – 3 P + 1,5 (100)
= 10 – 3 P + 150
Qd = 160 – 3 P
Qs = - 5 + 5 P – 0,5 T
= - 5 + 5 P – 0,5(50)
= - 5 + 5 P – 25
Qs = - 30 + 5 P
Ponto de Equilíbrio Inicial:
Qd = Qs
160 – 3 P = - 30 + 5 P
- 8 P = - 190
P0 = - 190 / - 8 = 23,75
Q0 = 160 – 3(23,75) = 88,75
P0 = 23,75
Q0 = 88,75
Exercício:
Equações Finais:
Qd = 10 – 3 P + 1,5 (200)
Ponto de Equilíbrio Final:
Qd = Qs
= 10 – 3 P + 300
310 – 3 P = - 20 + 5 P
Qd = 310 – 3 P
- 8 P = - 330
P1 = - 330 / - 8 = 41,25
Qs = - 5 + 5 P – 0,5 T
= - 5 + 5 P – 0,5(30)
Q1 = 310 – 3(41,25) = 186,25
= - 5 + 5 P – 15
Qs = - 20 + 5 P
P1 = 41,25
Q1 = 186,25
Mudança nas Curvas de Oferta e
Demanda
Equações Iniciais:
P
Qd = 160 – 3 P
S0
Qs = - 30 + 5 P
S1
P0 = 23,7
Q0 = 88,7
E1
41,2
E0
D1
23,7
Equações Finais:
Qd = 310 – 3 P
D0
Qs = - 20 + 5 P
P1 = 41,2
Q1 = 186,2
88,7
186,2
Q/t
Coeficientes de Elasticidades




Elasticidade-preço da demanda (Ed)
Elasticidade-preço da oferta (Es)
Elasticidade-cruzada da demanda (Ec)
Elasticidade-renda da demanda (Er)
Elasticidade-preço da demanda (Ed)
Mede a variação percentual
nas quantidades devido a
uma variação percentual nos
preços, ceteris paribus.


No arco: calculadas entre
dois pontos sobre a curva de
demanda;
(Q1  Q0 ) ( P0  P1 )
Ed 
( P1  P0 ) (Q0  Q1 )
Q
Q%
Q P
Q
Ed 


.
P% P P Q
P
Q = quantidade do bem
P = preço do bem
Δ = uma pequena mudanç
P
A
P0
M
P
B
P1
Q  Q1
Q 0
2
P P
P 0 1
2
Demanda
Q0
Q
Q1
Q/t
Elasticidade-preço da demanda (Ed)

Calcule Ed no arco para os
seguintes pontos:

A: P0 = 4 e Q0 = 20

B: P1 = 3 e Q1 = 50
P
A
4
Resolução:
M
P
B
3
Demanda
Ed = [(50 – 20) / (3 – 4)].[(3 + 4) / (20 + 50)]
20
Ed = (30 / -1).(7 / 70) = - 3
Q
50
Q/t
Elasticidade-preço da demanda (Ed)

No ponto: calculada num ponto sobre a curva de demanda;
dQ P
Ed 
.
dP Q
Q = a – b.P
P
Exemplo:
Dado Q = 20 – 4.P
Calcule a Ed quando P = 2.
Para P = 2  Q = 20 – 4(2) = 12
2
A
Ponto: P* = 2 e Q* = 12
Demanda
Ed = (- 4). (2 / 12) = - 0,66
12
Q/t
Elasticidade-preço da demanda (Ed)

Interpretação da Ed:
Ed = - 3

Um aumento no preço do bem de 1% levará a uma diminuição na
quantidade demandada em 3%.
Ed = - 0,66

Uma diminuição no preço do bem de 10% levará a um aumento na
quantidade demandada em 6,6%.
Ed = -0,66:
↓ 1%.P  ↑ 0,66%.Q
Ed = -0,66:
↓ 10%.P  ↑ 6,6%.Q
Classificação da Ed

Demanda Elástica:
Ed < - 1 ou |Ed| > 1
ΔQ% > Δ P%

Demanda Unitária:
Ed = -1 ou |Ed| = 1
ΔQ% = ΔP%

Demanda Inelástica:
Ed > -1 ou |Ed| < 1
ΔQ% < ΔP%
  < Ed < 0
Classificação da Ed
20%
18%
16%
14%
12%
10%
8%
6%
4%
2%
0%
Var.P%
Var.Q%
Inelástica
Unitária
Demanda
Elástica
Ed sobre a Demanda
|Ed| =
P

Em termos absolutos, a
elasticidade assume valores
decrescentes à medida que
percorremos a curva de
demanda de cima para
baixo.

|Ed| > 1
|Ed| = 1
M
|Ed| < 1
|Ed| = 0
Q
Ed e Demanda
P
P
P’
P’
P*
P*
Q
DEMANDA PERFEITAMENTE ELÁSTICA
Q*
Q
DEMANDA PERFEITAMENTE INELÁSTICA
Ed e Demanda
|EdA| < |EdB|
P
D
F
P’
A elasticidade não
determina a forma da curva
de demanda, embora exista
alguma relação com ela.
C
P
P*
QA
QB
QB’
QA’ Q*
DB
DA
Q
Demanda
Elástica
Demanda
Inelástica
Determinantes da Ed
As características determinantes da Ed
são:


Grau de necessidade do bem:
quanto maior a necessidade do bem,
menos elasticidade será o bem
(inelástico);

Disponibilidade de bens
substitutos: quanto maior o número
de substitutos, mais elástico será o
bem;

Proporção da renda gasta no bem:
quanto maior a parcela da renda gasta
no bem, mais elástico será o bem.

Tempo de ajuste às variações nos
preços de mercado: quanto maior o
horizonte de temporal, mais elástico
será o bem.
Tempo de ajuste às variações nos preços
dos bens:
P
P0
P
DLP
P1
QLP
DMP
QMP
QCP
Q0 QCP Q
MP
DCP
QLP
Q/t
Determinantes da Ed
P
M
|Ed| = 1
Q
Elasticidade-renda da demanda (Er)
Mede a variação percentual
da quantidade demandada
devido a uma variação
percentual na renda.

Classificação dos bens
segundo a Er:


Bens Normais
Er  0

Bens Inferiores
Er  0.
NO ARCO:
Q% (Q1  Q0 ) R0
Er 


R% ( R1  R0 ) Q0
Q0 e R0 são a quantidade demandada
e a renda no momento inicial;
Q1 e R1 são a quantidade demandada
e a renda no momento final.
NO PONTO:
dQs R
Er 
.
dR Q
Exercício:

Dada a equação de demanda de um bem:
Qd s  3.000 Ps  1.000 R  0,05Pop  1.500 Pc

Calcule a Er quando:
 Q = 8.000.000
 R = 10.000
dQds
 1.000
dR
dQds R
Er 
.
dR Q
10.000
Er  1.000
 1,25
8.000.000
Um aumento da renda em 1% levará ao aumento da quantidade
demandada em 1,25%, sendo portanto um bem normal.
Bens Inferiores x Bens Normais
BENS INFERIORES
BENS NORMAIS
Er < 0
Er > 0
Um aumento na renda resulta na
diminuição na demanda do bem.
Um aumento na renda resulta no
aumento da demanda do bem.
Elasticidade-cruzada da demanda (EXY)

Mede, em termos percentuais, como a quantidade demandada
do bem X responde às variações de preço do outro bem Y.

No Arco:
E XY
QX % (QX 1  QX 0 ) PY



PY %
( PY 1  PY 0 ) QX
QX= quantidade do bem X
PY = preço do bem Y

No Ponto:
E XY
dQ X PY

.
dPY Q X
Classificação dos
Bens segundo a EXY:
MERCADO DO FRANGO
P
B
P1
Bens Substitutos:
EXY  0
A
P0
Q1
Q0
Qf
MERCADO DO PEIXE
P
Exemplo: peixe e frango
Dfrango
A
B
P*
D1
D0
Q0
Q1
Qp
Classificação dos
Bens segundo a Ec:
MERCADO DO ARROZ
P
B
P1
Bens Complementares:
EXY  0
A
P0
Q1
P
Exemplo: peixe e arroz
P*
Darroz
Q0
Qa
MERCADO DO PEIXE
B
A
D1
Q1
Q0
D0
Qp
Classificação dos
Bens segundo a Ec:
P
P1
Bens Independentes:
EXY  0
MERCADO DE PARAFUSO
B
A
P0
Q1
P
Exemplo: peixe e parafuso
Dparafuso
Q0
Qpa
MERCADO DO PEIXE
A
P*
D0
Q0
Qp
Exercício:

Dada a equação de demanda para o bem S:
Qd s  3.000 Ps  1.000 R  0,05Pop  1.500 Pc

Calcule a ESC quando:
ESC


Qs = 9.500.000
Pc = 3.500
3.500
  1.500
9.500.000
ESC  0,55  0
Um aumento do preço do bem C em 1% levará ao aumento da quantidade
demandada do bem S em 0,55%, sendo portanto um bem substituto.
Elasticidade-preço da oferta (Es)

Mede a variação percentual da quantidade ofertada
devido a uma variação percentual do preço.

No Arco:

No Ponto:
Q
Q%
Q P
Q
Es 


.
P% P P Q
P
dQ P
Es 
. 0
dP Q
Elasticidade-preço da oferta (Es)

Classificação da ES:

Elástica: ES > 1

Unitária: ES = 1

Inelástica: 0 < ES < 1
Exercício:

Dada a equação de oferta:
Para P = 10, temos:
Qs = - 20 + 5.P
Qs = - 20 + 5(10)
= - 20 + 50

Calcule a ES quanto P = 10?
= + 30
dQ P
10
ES 
.  (5).  1,66
dP Q
30
Um aumento do preço do bem em 1% levará ao aumento da quantidade
ofertada do bem em 1,66%, sendo portanto um bem de oferta elástica.
Elasticidade-preço da Demanda, Receita das
Firmas e Despesas dos Consumidores:
Relação entre receita das firmas (R) e dispêndio
das famílias (D):


Os gastos das famílias são iguais às receitas das firmas,
uma vez que as famílias compram os bens e serviços
das firmas.
R = P.Q = D

Portanto, um aumento nos gastos das famílias
corresponde a um aumento na receita das empresas na
mesma magnitude.
Curva Receita = Despesas
P
Q
R=D
0
40
0
P
2
36
72
RT
4
32
128
20
6
28
168
8
24
192
10
20
200
12
16
192
14
12
168
16
8
128
18
4
72
20
0
0
Q=a–bP
R = P. Q = P (a – b.P)
R = a.P – b.P2
RMAX
A
M
D
0
R
40 Q
Análise Gráfica
P
O que acontecerá à Receita
das firma (ou Despesas das
famílias) se houver um
aumento ou diminuição do
preço do bem na faixa de
demanda elástica ou
inelástica?
RT
|Ed| > 1
20
|Ed| = 1
|Ed| < 1
M
RT
D
0
40 Q
Análise Gráfica
|Ed| = 1
P
RT

Na faixa de demanda
inelástica, um
aumento no preço do
bem resulta na
elevação da receita da
firma (ou despesas
das famílias).
|Ed| > 1
|Ed| < 1
20
A
168
128
M
6
C
B
4
0
28
32
D RT
40 Q
Análise Gráfica
|Ed| = 1
P
RT

Na faixa de demanda
elástica, um aumento
no preço do bem
resulta na diminuição
da receita da firma (ou
despesas das
famílias).
|Ed| > 1
|Ed| < 1
20
F
A
168
16
14
128
E
M
D RT
0
8
12
40 Q
Análise Gráfica
|Ed| = 1
P
DEMANDA
PREÇO
RECEITA=
DESPESA
RT
AUMENTO
AUMENTO
20
|Ed| < 1
A
INELÁSTICA
DIMINUIÇÃO
UNITÁRIA
|Ed| > 1
AUMENTO
DIMINUIÇÃO
DIMINUIÇÃO
CONSTANTE
M
ELÁSTICA
AUMENTO
DIMINUIÇÃO
DIMINUIÇÃO
AUMENTO
D RT
0
40 Q
Implicações da Relação Ed x Receita das
Firmas
Porque é importante conhecer a
relação entre a Ed e a Receita das
firmas?
Exercício:

Dada a equação de demanda:
Qd = 40 – 5.P

Diga o que ocorre com a Receita das firmas quando o preço de 5
sofre um aumento marginal?
Para P0 = 5
No Ponto:
 Q0 = 40 – 5.(5) = 40 – 25 = 15
Ed  (5).
5
 1,66
15
A Demanda sendo elástica, um aumento no preço do
bem faz a Receita das firmas diminuírem.