Indução Eletromagnética
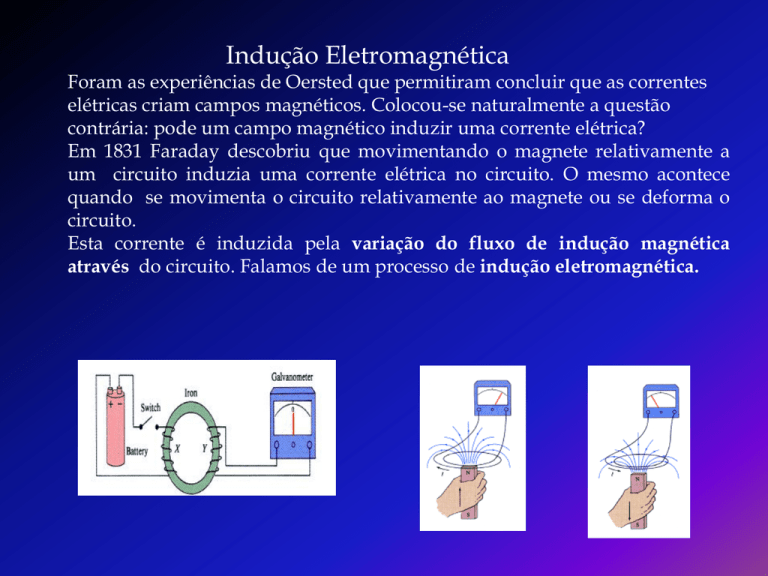
Foram as experiências de Oersted que permitiram concluir que as correntes
elétricas criam campos magnéticos. Colocou-se naturalmente a questão
contrária: pode um campo magnético induzir uma corrente elétrica?
Em 1831 Faraday descobriu que movimentando o magnete relativamente a
um circuito induzia uma corrente elétrica no circuito. O mesmo acontece
quando se movimenta o circuito relativamente ao magnete ou se deforma o
circuito.
Esta corrente é induzida pela variação do fluxo de indução magnética
através do circuito. Falamos de um processo de indução eletromagnética.
Indução Eletromagnética
Em todos os exemplos seguintes vai haver uma variação com o tempo do
fluxo de um campo magnético uniforme através do circuito indução
eletromagnética.
Aumento da área do circuito
deslocando um condutor em
contacto com um circuito em U
Espira a rodar num campo magnético
= B A cos
Deformação de uma espira submetida a
um campo magnético provocando variação
da superfície
Na situação do slide anterior, o campo magnético tem um valor
B=0,50 T e a superfície mostrada tem uma área de 0,01 m² (100cm²).
Calcule o valor do fluxo magnético por meio da superfície supondo
que:
a) θ = 60°
b) θ = 0°
c) θ = 90°
Lei de Faraday - Newman
A força eletromotriz induzida (fem) em um circuito fechado é
determinada pela taxa de variação do fluxo magnético que
atravessa o circuito.
ε = - /t
Lei de Lenz
Lei de Lenz: a f.e.m. induzida e a corrente induzida surgem
com um sentido que se opõe à variação que as provocou.
A corrente induzida vai gerar um fluxo de indução magnética
que se vai opor à variação de fluxo de indução magnética que a
gerou.
Quando a barra se move para a espira, o fluxo
magnético através da espira aumenta. A corrente aí
induzida cria um campo magnético (a tracejado) cujo
fluxo se vai opor ao aumento de fluxo magnético
através da espira (provocado pelo movimento da
barra).
Um eletroímã gera um campo magnético B1=0,3 T em uma espira
circular de área 0,02 m² e resistência 5,0 Ω. Ao aproximar este
eletroímã da espira, em 0,2 s, o campo passa a ser B2=0,8T.
Determine:
a) a força eletromotriz induzida na espira.
b) a intensidade da corrente induzida na espira.
Transformador
• Um transformador é um dispositivo para modificar tensões e correntes
alternadas sem perda apreciável de potência.
• Um transformador simples é constituído por dois enrolamentos em torno de
um núcleo de ferro. O enrolamento que recebe a potência é o primário, o outro o
secundário.
10
10
U1
U2
Volt
Volt
i2
i1
N1
N2
i2
i1
N1 = U1
N2 U2
4 espiras
8 espiras
N1 = i2
N2 i1
a)
b)
Um transformador de tensão possui 100 espiras em seus rolamentos
primários e 500 espiras nos rolamentos secundários. Ligando-se o
primário desse transformador a uma fonte de tensão alternada de
120 V, verifica-se que o primário é percorrido por uma corrente de
intensidade 2,0 A.
Calcule a voltagem no secundário desse transformador
Determine a intensidade da corrente no secundário desse
transformador.
Condutor em movimento dentro de um campo magnético
Consideremos um condutor metálico, movimentando-se com
velocidade V, perpendicularmente às linhas de indução de um campo
magnético B.
N
B
V
V
B
S
Vista de Cima
•
Podemos então dizer que existe uma diferença de potencial entre as
extremidades do condutor. A essa ddp damos o nome de força
eletromotriz induzida (e ou fem).
e
FM
Vista de Cima
V
B
Cálculo da força eletromotriz induzida
L = comprimento do condutor dentro do
campo magnético (metros);
B = intensidade do campo magnético
uniforme (tesla);
V = velocidade de deslocamento (m/s);
V perpendicular a B ;
e = força eletromotriz induzida (volts).
e B L V
Exemplo
Um condutor AB de comprimento 30cm move-se em um plano horizontal
apoiado em dois trilhos condutores que estabelecem um circuito conforme
a figura a seguir. O condutor é arrastado pelos trilhos com velocidade
constante igual a 10m/s.
A
Assim determine:
a) o sentido convencional da
corrente no condutor AB;
b) a fem induzida no condutor;
c) a intensidade da corrente que
percorre o condutor.
V
R= 2
B
B= 101T
B
Solução
A
Sentido
real
Sentido
convencional
V
R= 2
B
B= 101T
B
Solução
A
Sentido
convencional
R= 2
B 101T
Dados L 30cm 3 101 m
V 10 m s
e
FM
B
B= 101T
e B L V 101 3 101 10
e 0,3volt
V
B
e 0,3V
Dados
R 2
e
0,3
R
2
i 0,15A
i
Aplicação da indução eletromagnética
• O gerador de energia elétrica:
Auroras boreal e austral
GARRAFA MAGNÈTICA
CINTURÃO DE VAN ALLEN
CINTURÃO DE VAN ALLEN
AURORA BOREAL












