Slide 1

Eletrônica de Potência
5. Retificadores não controlados
 Sumário
• Cargas lineares e não-lineares.
• Distorsão e fator de potência.
• Classificação de conversores CA/CC “Front-Ends”.
• Limitando altas correntes de partida “Inrush Currents”.
• Retificadores monofásicos.
• Retificadores trifásicos.
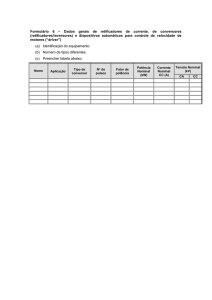
 Cargas Lineares
Prof. Ricardo Ribeiro
Fevereiro/2006
1
Eletrônica de Potência
5. Retificadores não controlados
 Cargas Não - Lineares
• Distorção Harmônica:
• Fator de Potência de Deslocamento:
• Fator de Potência:
• Cargas não-lineares reduzem o fator de potência.
Prof. Ricardo Ribeiro
Fevereiro/2006
2
Eletrônica de Potência
5. Retificadores não controlados
 Cargas Não - Lineares
• A relação PF/DPF decresce com o aumento da distorção harmônica.
Prof. Ricardo Ribeiro
Fevereiro/2006
3
Eletrônica de Potência
5. Retificadores não controlados
 Cargas Não - Lineares
• Normas Técnicas – IEEE 519
• Limite de harmônicos de corrente para cargas com vários valores relativos.
• As amplitudes relativas das correntes de carga são baseado na corrente de
curto-circuito.
Prof. Ricardo Ribeiro
Fevereiro/2006
4
Eletrônica de Potência
5. Retificadores não controlados
 Tipos de retificadores – Front-Ends
• (a) retificador a diodo, (b) retificador chaveado e (c) retificador a tiristor.
• Evitando corrente altas de partida – “Inrush Currents”
Prof. Ricardo Ribeiro
Fevereiro/2006
5
Eletrônica de Potência
5. Retificadores não controlados
 Retificadores monofásicos
Carga indutiva
A corrente i é dada por
vs  Ri  L
di
dt
em que a tensão no indutor é
1
vL dt  di
L
ou seja,
i ( t3 )
1 t3
vL dt   di 
i (0)
L 0
 i(t3 )  i(0)  0
então:

t3
0
vL dt  0
Prof. Ricardo Ribeiro
Fevereiro/2006
6
Eletrônica de Potência
5. Retificadores não controlados
 Retificadores monofásicos
A interpretação gráfica da Eq.
anterior pode ser expressa,

t1
0
ou,
t3
vL dt   vL dt  0
t1
Área A  ÁreaB  0
Carga com tensão CC interna
• O diodo conduz, quando vs > Ed.
• O valor máximo de i ocorre
quando vs = Ed.
• O critério de igualdade das
áreas A e B, também é satisfeita.
Prof. Ricardo Ribeiro
Fevereiro/2006
7
Eletrônica de Potência
5. Retificadores não controlados
 Retificadores monofásicos
Carga fonte de corrente
A tensão de saída do retificador é
vd (t )  vs
conseqüentemente, a corrente de entrada
is é dada por:
 id se vs  0
is (t )  
 id se vs  0
O valor médio da tensão de saída é
T /2
1
2Vs sin tdt 

0
(T / 2)
1
2

( 2Vs cos t ) |T0 / 2  Vs
T / 2

2
Assim, Vd 0  Vs  0.9Vs
Vd 0 

Prof. Ricardo Ribeiro
Fevereiro/2006
8
Eletrônica de Potência
5. Retificadores não controlados
 Retificadores monofásicos
Carga fonte de corrente
Como a carga é uma fonte de corrente Is = Id, por Fourier:
I s1 
2

2 I d  0.9 I d
 0 se h  par
I sh  
I s1 / h se h  ímpar
e
conseqüentemente, a taxa de distorção harmônica da corrente é
THDi  48,43%
e portanto,
DPF  1.0
FP  DPF
I s1
 0.9
Is
Efeito de Ls na comutação de corrente
 A introdução da indutância da fonte Ls,
impõe um atraso na transição de corrente.
Prof. Ricardo Ribeiro
Fevereiro/2006
9
Eletrônica de Potência
5. Retificadores não controlados
 Retificadores monofásicos
Efeito de Ls na comutação de corrente
A tensão no indutor é dada por:
vL  2Vs sin t  Ls
para 0  t  
dis
dt
em que,
dis
dis
Ls
 Ls
dt
d (t )
então:
2Vs sin td (t ) 
 Ls dis
Circuitos equivalentes 1Ф para a comutação de corrente
Assim:
Prof. Ricardo Ribeiro
Fevereiro/2006
10
Eletrônica de Potência
5. Retificadores não controlados
 Retificadores monofásicos
Efeito de Ls na comutação de corrente
Integrando-se ambos lados a Eq. anterior (vL), obtém-se que:


0
Id
2Vs sin td (t )  Ls  dis Ls I d
0
O lado esquerdo da Eq. acima, representa a área Aμ, ou seja:
A  

0
2Vs sin td (t )  2Vs (1  cos  )  Ls I d
conseqüentemente,
cos   1 
Ls I d
2Vs
No caso de Ls = 0, a tensão de saída do retificador é dada por
1
Vd 0 
2


0
2Vs sin td (t ) 
1
Na existência de Ls, Vd 
2
Prof. Ricardo Ribeiro


2 2
Vs  0.45Vs
2
2Vs sin td (t )
Fevereiro/2006
11
Eletrônica de Potência
5. Retificadores não controlados
 Retificadores monofásicos
Efeito de Ls na comutação de corrente
A expressão anterior pode ser reescrita como:
1
Vd 
2


0
1
2Vs sin td (t ) 
2


0
2Vs sin td (t )
o que corresponde a,
Vd  0.45Vs 
areaA
2
 0.45Vs 
Ls I d
2
em que a redução da tensão de saída, decorrente de Ls é
Vd 
areaA
2

Ls I d
2
a extrapolação para o retificador de onda completa pode ser feita como:
A  

Id
2Vs sin td (t )  Ls  dis  2Ls I d
Id
areaA
2Ls I d
2Ls I d
cos   1 
 Vd  Vd 0 
 0.9Vs 


2Vs
0
Prof. Ricardo Ribeiro
Fevereiro/2006
12
Eletrônica de Potência
5. Retificadores não controlados
 Retificadores monofásicos
Efeito de Ls na comutação de corrente – Retificador onda completa
Prof. Ricardo Ribeiro
Fevereiro/2006
13
Eletrônica de Potência
5. Retificadores não controlados
 Retificadores monofásicos
Carga fonte de tensão
No gráfico ao lado:
1. θb é o instante de início
da corrente id.
2. θp é o instante em que id
é máxima.
O ângulo θb pode ser calculado por:
Vd  2Vs sin b
Prof. Ricardo Ribeiro
Fevereiro/2006
3. θf é o instante em que id
se anula.
14
Eletrônica de Potência
5. Retificadores não controlados
 Retificadores monofásicos
Carga fonte de tensão
O ângulo θp, em que id atinge o seu valor máximo é dado por:
 p    b
A tensão no indutor, pode ser dada por:
vL  Ls
did
 2Vs sin t  Vd
dt
Integrando-se ambos os lados,


b
b
Ls  did   ( 2Vs sin t  Vd )dt
p 
para
como id em θb é igual a zero, então:
1
id ( ) 
Ls

 (
2Vs sin t  Vd )dt
b
mas id também vai pra zero em θf, assim:
0   ( 2Vs sin t  Vd )dt
o que corresponde a igualdade de áreas A e B.
Prof. Ricardo Ribeiro
Fevereiro/2006
f
b
15
Eletrônica de Potência
5. Retificadores não controlados
 Retificadores monofásicos
Carga fonte de tensão
O valor médio de Id pode ser obtido como:
f
Id



id ( )d
b

Modelo dinâmico de um circuito retificador
O circuito equivalente do retificador é apresentado na Fig. acima.
Para tb < t < tf,
Para tf < t < tb+T/2
Conseqüentemente,
Prof. Ricardo Ribeiro
did
dv
v
 vd
id  Cd d  d
dt
dt Rload
dvd
vd
id  0 

dt
Cd Rload
vs  Rs id  Ls
vd (t )  vd (t f )e
 ( t t f ) / Cd Rload
Fevereiro/2006
16
Eletrônica de Potência
5. Retificadores não controlados
 Retificadores trifásicos
Carga fonte de corrente
A tensão de saída é dada por:
vd  vPn  vNn
Prof. Ricardo Ribeiro
Fevereiro/2006
17
Eletrônica de Potência
5. Retificadores não controlados
 Retificadores trifásicos
Carga fonte de corrente
A corrente da fase a pode ser dada por
O valor médio da tensão de saída é
Vd 0 
 I d se D1  1

ia    I d se D4  1
0 se D  D  0
1
4

1  /6
3 2
2
V
cos

td
(

t
)

VLL  1.35VLL
LL



/
6
 /3

O valor rms da corrente de fase é dado por:
Is 
2
Id
3
Por Fourier, a fundamental da corrente de fase é
I s1 
1

6 I d  0.78I d
conseqüentemente,
DPF  1.0
Prof. Ricardo Ribeiro
FP  DPF
Fevereiro/2006
I s1 3
  0.955
Is 
18
Eletrônica de Potência
5. Retificadores não controlados
 Retificadores trifásicos
Carga fonte de corrente – efeito de Ls
O circuito equivalente de um instante
de comutação é apresentado ao lado.
Neste instante,
ia  0
ic  I d  ia
Assim, as tensões nas indutâncias são:
vLa  Ls
di
dia
 Ls 
dt
dt
di
dic
vLc  Ls
  Ls
dt
dt
A tensão na malha vcomm é
vcomm  van  vcn  vLa  vLc  2 Ls
Prof. Ricardo Ribeiro
di
dt
Fevereiro/2006
19
Eletrônica de Potência
5. Retificadores não controlados
 Retificadores trifásicos
Carga fonte de corrente – efeito de Ls
Desta forma,
Ls
di
dt

van  vcn
2
Integrando-se ambos os lados, obtém-se que:
Id

0
0
Ls  di  
como: van  vcn  2VLL sin t
então:
Ls 
Id
0
van  vcn
d (t )
2
2Ls I d
2VLL (1  cos  )
di  Ls I d 
 cos   1 
2
2VLL
similarmente, o valor da área Aμ é dado por
Ls I d
A  Ls I d  Vd 
 /3
Prof. Ricardo Ribeiro
ou
Fevereiro/2006
Vd  Vd 0  Vd  1.35VLL 
Ls I d
 /3
20