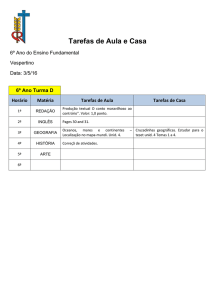
Unidade teórica 4
. O Modelo simplificado de Sharpe (1963)
Avaliação de activos financeiros: Modelo C.A.P.M.
(Notas de Moukhamedjanova Sabina
Chan Bonnie e de
Abhishek Kapur & Geir Sivertsen)
Carlos Arriaga Costa
2005/06
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
1
.Bibliografia
Eugene
F. Fama e Merton H. Miller
The Theory of Finance (Hinsdale,
Illinois: Dryden Press, 1972) Cap 7.
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
2
Eficiência segundo Markowitz – baseado na média e
na variância
Considere N activos num portfolio e as
seguintes notações :
Vector de ponderações
w=[w1 . . . wN]
Matriz das variâncias-covariâncias
Ω
Vector de retornos
R=[R1 . . . RN]
Vector unitário
1=[11 . . . 1N]
Variância do portfólio
wT Ω w
Economia Financeira - unid 4
T
Retorno do portfólio
Mestrado Economia UM_EEG- 4ºw R
unid 4 Carlos Arriaga
Costa
curso
3
Fronteira do Portfolio
Retornos do portfolio : wT R
Variância do Portfolio : wT Ω w
3
2
1
4
6
5
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
4
Efficiencia segundo Markowitz
(Média-Var)
Para encontrar a fronteira de eficiência
min wT Ω w
s.a.
w
1=1T w
r=RT w
Optimização :
min
w
unid 4 Carlos Arriaga
Costa
1
2
wT Ω w + (1-1T w) + (rRT w)
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
5
FOC :
Eq. 1 : Ωw=1 + R
Eq. 2 :w=Ω-11 + Ω-1 R
Multiplicando equação 1 por 1T e RT :
Eq. 3 :1=a +b
Eq. 4 : r=b +c
onde : a=1T Ω-11, b=1T Ω-1R, c=RT Ω-1R
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
6
Resolvendo em ordem a e nas equações 3 e 4,
e substituindo na eq 2, obtem-se :
w=v1+v2 r
V1 e v2 são dois vectores fixos.
Por outro lado, qualquer combinação convexa de
portfolios eficientes é também um portfolio
eficiente.
O portfolio de mercado não é mais do que uma
combinação ponderada de portfólios, e que,por
sua vez também é eficiente.
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
7
Modelo simplificado de Sharpe
Problemas do Modelo de Markowitz: Grande
dimensão da matriz de co-variâncias (cálculo
computacional complicado em 1959)
Conhecimento da matriz das co-varâncias
Hipótese de Sharpe (1963): Os rendimentos dos
diversos activos encontram-se ligados entre eles
por uma relação a um factor comum subjacente:
Ři = αi + βi Ĩ + ũi
Ĩ = αn+1+ vn+1
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
8
CAPM
– Mossin, Jan. “Equilibrium in a Capital
Asset Market.” Econometrica 34(Oct.
1966): 768-83.
– Sharpe, W. F. “Capital Asset Prices: A
Theory of Market Equilibrium under
Conditions of Risk.” Journal of Finance
19(Sept. 1964): 425-42.
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
9
– Lintner, John. “Security Prices, Risk, and
Maximal Gain from Diversification.”
Journal of Finance 20(Dec. 1965): 587615.
– Lintner, John. “The Valuation of Risk
Assets and the Selection of Risky
Investments in Stock Portfolios and
Capital Budgets.” Review of Economics
and Statistics 47(Feb. 1965): 13-37.
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
10
Avaliação de activos financeiros: Modelos
C.A.P.M. e A.P.T.
Capital market theory (derivado do modelo de Sharpe)
SEcurity market line: Determinação do valor de um activo,
tendo em conta o activo sem risco e o portfólio de mercado.
CAPM : Capital Asset Pricing Market: Modelo de avaliação
dos activos financeiros tendo em conta a relação entre o
modelo de mercado e a security market line.
APT: Arbitrage Pricing theory : Os rendimentos dos cativos
financeiros são função lineares de mais do que um factor
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
11
O papel do activo sem risco no
modelo
O
equilíbrio de mercado oferece
dificuldades de representação porque
diferentes investidores têm
assumpções diferentes quanto ao
risco. A introdução do activo sem
risco resolve esta ambiguidade.
– O activo sem risco reduz o número
potencial de portfolios eficientes a um
único portfolio.
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
12
mp
rp
rf
unid 4 Carlos Arriaga
Costa
sp
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
sp
13
– Dentro deste equilíbrio, existe apenas
um portfolio eficiente. Qualquer grau de
aversão ao risco pode ser retratado no
modelo através de uma combinação de
um portfolio simples e eficiente e um
emprestimo ou emprestar (borrowing ou
lending) à taxa sem risco.
– Substituindo xm por xp ou deixando que
o “portfolio índice” seja o portfolio de
mercado eficiente, ter-se-á:
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
14
1 s m
m j m m ~ s m
1 x j
1
1
unid 4 Carlos Arriaga
Costa
m
m
rf
sm
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
15
m m rf s m
m j rf
~
s m x j
m m rf s jm
rf
sm sm
rf j m m rf
s jm
j 2
sm
unid 4 Carlos Arriaga
Costa
rit i rmt it
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
16
Conceitos
Borrowing Portfolio
Um
investidor é capaz de se
endividar de maneira a comprar um
montante de um portfólio cujo valor
seja superior aos valores iniciais:
E(Řp) = Xzrz + (1-Xz)rb
rb
é a taxa de empréstimo
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
17
Conceitos
Lending portfolio
Emprestador sobre o mercado monetário (sem
risco) e associação à aquisição de activos com
risco.
Condições :
- Existe ao menos alguem que não apresenta
risco de não cumprimento da dívida (quem pede
emprestado com risco nulo)
- O rendimento presente e futuro de quem
adquire este activo é um valor certo
- Este activo oferece uma protecção perfeita
contra a perda do poder de compra
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
18
MODELO CAPM
O CAPM considera que todos os investidores possuem portfolios
eficientes no sentido de maior valor esperado para um mínimo
risco.
Pelo teorema de separação de dois portfolios, o portfólio de
mercado é também eficiente.
Para a validade do CAPM, o portfolio de mercado deve encontrarse na fronteira eficiente.
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
19
Condições de estimação do modelo de mercado
O índice de mercado deverá responder às
condições seguintes:
1. Ser exaustivo , isto é, deverá ser
calculado a partir de todos os activos
financeiros com risco existente no
mercado (vinte são representativos)
2. Ser um indice de rendimento e não
apenas um índice de preços. Deverá ter
em conta os rendimentos líquidos
distribuídos (dividendos e juros).
3. Ser um índice
ponderado e não uma
Economia Financeira - unid 4
unid média
4 Carlos Arriagaaritmética
Mestrado simples.
Economia UM_EEG- 4º
Costa
curso
20
Versões do CAPM
Sharpe-Lintner : E[Zi]=i + ßi (E[Zm])
Este activo assume a presença de um
Activo sem risco
Black :
E[Ri]= i + ßi (E[Rm])
Este modelo trata a taxa sem risco como uma variável
aleatória
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
21
Problema de minimização
Black version
minN wTVw s.t. 1T w 1 and RT w R
wR
Sharpe-Lintner (com activo sem risco)
minN wTVw s.t. (R R01)T w R R0
wR
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
22
Sharpe Model
Regressão de Zit sobre Zmt
Hipótese nula :
0 0
Versão de Black
Regressão
E[ Rt ] i E[ Rmt ] (i ) E[ Rmt ]
Hipótese nula α = (i-β)γ
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
23
Modelo de Sharpe-Lintner
A solução de SharpeLintner é uma
fronteira de eficiência.
Esta fronteira de
eficiência combina
uma posição longa no
portfolio de mercado
com um activo sem
risco adquirido em
situação de “lending”
ou “borrowing”
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
24
Black CAPM
R p Rz ( m ) pm ( Rm Rz ( m ) )
R p (1 pm ) Rz ( m ) pm Rm
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
25
Security Market Line
E(Rp)
E(rm)
y
rf
Zero Beta Portfolio
unid 4 Carlos Arriaga
Costa
1
σ (p)
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
26
Security Market Line
• Derivamos a security
market line:
R p R0 pm ( Rm R0 )
• Em forma de retorno
em excesso
R p R0 pm ( Rm R0 )
Zit pm Z mt
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
27
Como testar o CAPM?
Os testes do CAPM focam-se em três implicações do modelo
de excesso de retorno
A intercepção é zero
Beta captura completamente a variação
dos retornos em excesso.
O prémio de mercado é positivo.
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
28
Testes sobre a “intercept”
Sharpe-Lintner :
E[Zi]= i + ßi (E[Zm])
Testar se i = 0
Black :
E[Ri]= i + ßi (E[Rm])
Testar se
i = (1-ßi) E[R0]
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
29
Zero-Beta CAPM
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
30
Pressupostos implicitos do modelo
As estimativas encontram-se sujeitas a erro de
amostragem pelo que o portfolio de mercado não
é suposto ser ex-post eficiente.
A medida do racio de sharp mede a ineficiencia
do portfolio de mercado que nos permite
detrminar quando deveremos rejeitar o CAPM.
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
31
Rácio de Sharpe
Dada uma tangente a, e um
portfolio de mercado m :
A diferença ra - rm dános uma medida da
ineficiência de m
unid 4 Carlos Arriaga
Costa
a
rf
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
m
32
Oferta de acções pela empresa
Assumimos que cada empresa vende
acções a um preço Pi. Os Investidores
desejam adquirir estas acções
fundamentados no valor futuro da
empresa no final do período, Vi. O valor
de aquisição e o valor da empresa no final
do período determinarão a taxa de
retorno:
unid 4 Carlos Arriaga
Costa
Vi Pi
Ri
Pi
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
33
O valor futuro da empresa implica algum
risco, por isso a taxa de retorno possui
risco. Por outro lado, todos os
investidores avaliam o investimento
considerando o equilibrio da linha de
“capital market”.
Matematicamente, o preço e o valor do
portfolio de mercado fica:
N
N
i 1
i 1
Pm Pi e Vm Vi
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
34
Vm Pm 1 Rm
E V j Pj
Pj
unid 4 Carlos Arriaga
Costa
E Rm R f
Rf
sm
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
s jm
Pjs m
35
Incorporano o risco usando o
CAPM
Os
ajustamentos ao risco advêm da
última equação (taxa de desconto
ajustada ao risco) .
Reduzindo a expressão à formula do
CAPM
R j R f j Rm R f
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
36
A
taxa de desconto ajustada ao risco
pode ser utilizado na análise do valor
presente:
ECF I t
N
PV
i 1
unid 4 Carlos Arriaga
Costa
1 R
f
j Rm R f
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
i
37
Reformulando
1
j
R
j
a equação
R f RM R f
Esta aproximação leva-nos a transformar
as taxas anuais de retorno a “certainty
equivalents” baseados no portfolio de
mercado:
Economia Financeira - unid 4
unid 4 Carlos Arriaga
Costa
Mestrado Economia UM_EEG- 4º
curso
38
1
E CF I t
N
j
PV
i
1 Rm
i 1
unid 4 Carlos Arriaga
Costa
Economia Financeira - unid 4
Mestrado Economia UM_EEG- 4º
curso
39