Slide 1 - DEE UFBA

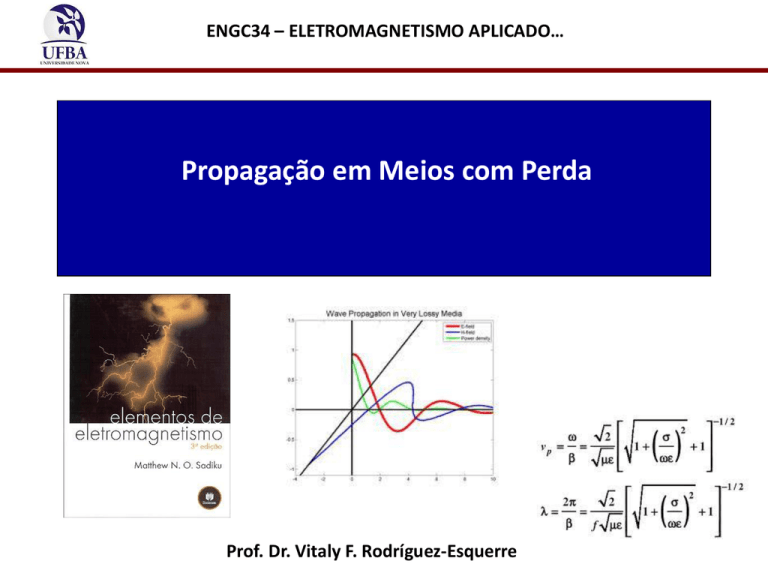
ENGC34 – ELETROMAGNETISMO APLICADO…
Propagação em Meios com Perda
Prof. Dr. Vitaly F. Rodríguez-Esquerre
Considere um meio com perdas, caracterizado pela sua condutividade s,
porem sem cargas livres.
As equações de Maxwell para campos harmônicos são escritos da
seguinte forma:
Aplicando o rotacional na Eq (10.13)
Fazendo uso da identidade vetorial
e da Eq. (10.14)
Obtem-se
Ou
Onde
 é conhecida como constante de propagação, e será uma variável complexa,
Podendo ser expressa na forma,
de forma similar pode ser obtida uma equação para o campo magnético,
Para obtermos os valores de a e b na Eq. (10.20) faremos o seguinte:
Resolvendo o sistema de equações (10.21) e (10.22) obtem-se
Consideremos um campo propagando na direção +z, com apenas uma
componente em x,
Substituindo na Eq. (10.17), obtem-se
Colocando em evidencia o operador laplaciano, lembrando que não existe
variação na direção x e y
Obtem-se a equação diferencial,
Cuja solução tem a forma,
Como o campo deve ser finito em z=infinito, considera-se apenas a
exponencial negativa, o campo E(r,t) pode ser então escrito como,
Resultando em ,
E  z, t   E0ea z cos t  b z  xˆ
ES  z   E0e z xˆ
d 
ˆ
  ES  z     E0e x   zˆ   E0e  z xˆ   E0e  z yˆ
 dz 
  E0  z    j H S  z 
 z
 E0 e  z yˆ   j H S  z 
 E0 e  z
H yS  z  
 j
H yS

 z 

j s  j E0 e  z
j
E0 e  z
s  j
 z
H yS  z  
E0 e 
j

De forma analoga, pode ser obtida a solução da Eq. (10.19)
Onde
é conhecida como impedância do meio e será complexa
Onde
O ângulo q varia entre 0 e 45 graus.
Substituindo (10.31) e (10.32) em (10.30)
H  z, t  
E0

e
a z
cos t  b z  q  yˆ
Observe a defasagem entre os campos,
E  z, t   E0ea z cos t  b z  xˆ
As propriedades de propagação são calculadas usando
Podemos também re-escrever a Eq (10.14)
onde
Ou
onde
Distância de Penetração (m)
Questão 1 (3,5 pontos)
Faça um gráfico em escala logarítmica da distância de penetração vs. frequência para
água do mar considerando os seguintes parâmetros: er=80, mr=1, s=4 S/m e f [1 KHz, 10
GHz]. Comente seus resultados.
3
10
4
10
5
10
6
10
7
10
8
10
9
10
10
10
Frequência (Hz)
Em 1 MHz, determine a impedância intrínseca, defasagem entre E e H, e velocidade
de fase da onda.
A que profundidade a densidade de potência média será 1% do valor presente logo
abaixo da superfície da água?
EXEMPLO
Considere um campo que incide na água do mar
Z=0
Determinar, constante de atenuação, constante de propagação, constante de
fase, Impedancia intrínseca, velocidade de fase, comprimento de onda,
distancia de penetração
Determinar a distancia em que o campo é 1 V/m
Escrever as expressões de E(0,8, t) e H(0,8, t)
Determinar a distancia em que o campo é 1 V/m
Uma equipe de cientistas está projetando um radar para
medir a espessura do gelo sobre a terra. Para detectar o
eco na interface gelo‐terra, a espessura do gelo deve ser de
no máximo 3 vezes a distância de penetração da onda no
gelo. Sabendo que a máxima espessura de gelo é 1,2 km,
Determinar qual é a faixa de freqüências que pode ser
usada (εr = 3 – j 0,01)
hmax  0,8Km
Gelo
TERRA
Deseja-se enviar um sinal de rádio para o receptor da
mergulhadora.
Se a densidade de potência mínima que pode ser detectada
pelo receptor da mergulhadora é de 1 uW/m2, determine o
valor mínimo do campo elétrico logo acima da superfície da
água.
Em f = 1 KHz;  r '  80 e a condutividade é 1,0 S/m.
Considere incidência normal na interface ar-água.
0
AR
AGUA
-2
z (m)
-4
-6
-8
-10
E0 T  0,774 mV/m T  0,000471 E0  1, 64 V/m
0m
E0e
a z
=0,5 mV/m
a  0, 0628 Np/m
 r  80  j
2
-7 m
s
 0
1
1 E
S av  Re  E  H * 
cos q n  1, 0  W
2
2 
z  7 m
E0  0, 774 mV/m
  0, 063  j 0, 063
  0, 08845 E  0,5 mV/m
Se o campo elétrico de um sinal acima da superfície da água é
de 1 V/m, quais submarinos conseguem receber esse sinal se o
mínimo campo elétrico que pode ser detectado é |E|= 0,01 V/m
? Escreva as expressões do campo e para o submarino que
detecta o sinal com menor amplitude.
Em f = 1,4 MHz; a permissividade relativa da água do mar é .
Explique todas as considerações realizadas.
 r  74,83  j56,01
f=1.4 10^6
w=2 Pi f
u0=4 Pi 10^-7
e0 = 8.85 10^-12
n0=Sqrt[u0/ e0]
e1=e0 (74.83-I 56.01)
n1=Sqrt[u0/e1]
Arg[n1] 180 / Pi
R=(n1-n0)/(n1+n0)
T=1+R
T = Abs [T]
k1=w Sqrt[u0 e1]
El=T Exp[-0.08955563803396899 z]
Solve[El==0.01,z]
Plot[El,{z,0,100},PlotRange->All]
56*w*e0
1.4×106
8.79646×106
p/2500000
8.85×10-12
376.819
6.62245×10-10-4.95688×10-10 j
36.9818?+12.3075 j
18.4074
-0.819648+0.0541209 j
0.180352?+0.0541209 j
0.188297
0.269099-0.0895556 j
0.188297 Exp[-0.0895556 z]
z=32.7778
0.15
0.10
0.05
20
40
60
80
100