PARÂMETROS_IDENTIFICAÇÃO

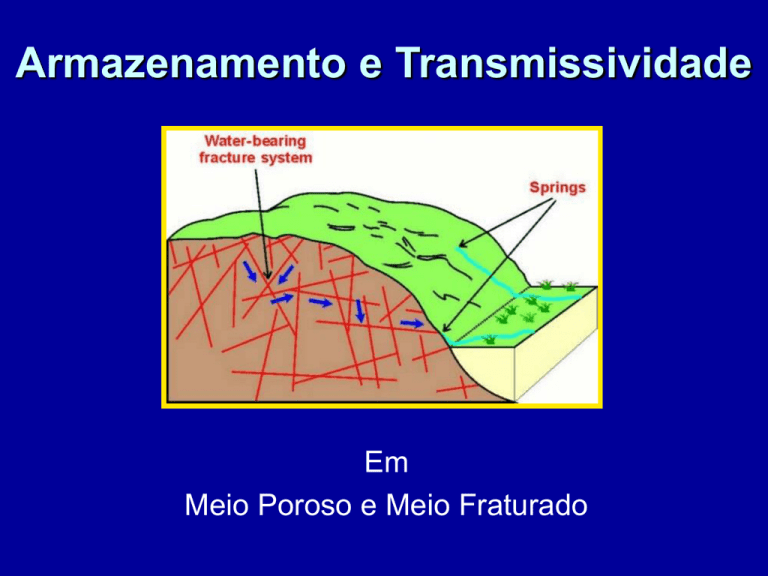
Armazenamento e Transmissividade
Em
Meio Poroso e Meio Fraturado
• A caracterização do regime de águas
subterrâneas em rochas fraturadas pode
ser feita com base em métodos de testes
hidráulicos simples e métodos analíticos.
• Transmissividade e Coeficiente de
armazenamento são oriundos de
métodos analíticos para meio poroso
(fluxo radial) que não representam as
condições de contorno muito mais
complexas inerentes dos aqüíferos
fraturados.
• Métodos analíticos são frequentemente
utilizados para estimar a
Transmissividade (T) e o Coeficiente de
Armazenamento (S) de um aqüífero.
• O modelo clássico analítico é o modelo de
Theis (1935), que é usado para aqüíferos
confinados homogêneos e isotrópicos.
• Via de regra, o meio fraturado é mais
complexo que o meio poroso porque o
escoamento pode ocorrer em conduítes
distintos e possivelmente na matriz de
poros.
• A caracterização da geometria,
localização e conectividade das
fraturas é essencial para se interpretar a
resposta do aqüífero ao bombeamento.
Na grande maioria dos aqüíferos
fraturados a resposta difere
significativamente da predita por Theis.
• O desenvolvimento da
teoria do escoamento em
meio poroso começou com
o trabalho experimental de
Henri Darcy, publicado em
1857.
• O estudo do escoamento
através de rochas
fraturadas foi primeiro
desenvolvido na industria
do petróleo.
• Estes estudos resultaram de
observações que a produção de óleo e
gás podia ser significativamente
aumentada por se fraturar as
formações rochosas nas proximidades
dos poços.
• O escoamento de águas subterrâneas no
meio fraturado é primariamente
controlado pelas fraturas. Como
resultado, o fluxo pode seguir caminhos
tortuosos devido ao alto grau de
heterogeneidade espacial induzida pelas
fraturas.
Condutividade Hidráulica:
• A condutividade hidráulica de um aqüífero, K
[m/s], é a propriedade que descreve a
capacidade da água de escoar através do meio
poroso. Ela pode ser decomposta em 3 termos:
K = k/
Onde:
k [m²] é a permeabilidade intrínseca;
 [Pa/m] é o peso específico do fluido;
 [Pa.s] é a viscosidade dinâmica do fluido;
Na indústria do petróleo a lei de Darcy é
frequentemente escrita na seguinte forma:
q
k


Onde:
 = h [Pa] é o potencial total;
A permeabilidade
intrínseca, k, está
relacionada com o
tamanho do poro no
meio granular na
seguinte forma:
k = Cd²
Onde:
C é uma constante;
d é o diâmetro médio do
poro;
Para o meio fraturado
temos:
k=e²/2
Onde e é a abertura da
fratura.
Note que k cresce com
o quadrado do
diâmetro médio do
poro ou da abertura
da fratura!
• A complexidade do escoamento através
das fraturas torna inadequado o uso das
técnicas clássicas de interpretação dos
testes hidráulicos.
• O armazenamento no cristalino fraturado
é geralmente baixo.
• Como conseqüência, pequenas
quantidades de injeção ou de descarga
dos poços construídos nestas rochas
pode ter um efeito mensurável nos níveis
da água da região circunvizinha.
Movimento das águas subterrâneas
nas rochas cristalinas fraturadas
• As rochas cristalinas são de difícil
caracterização; assim, o movimento das
águas subterrâneas é de difícil predição.
• O escoamento nas rochas cristalinas
ocorre nas fraturas, mas nem todas as
fraturas conduzem água.
• O escoamento realmente se dá nas
partes das fraturas que estão conectadas
a uma fonte de água e que podem
conduzir o escoamento (ver figura).
• O armazenamento é baixo comparado
com a condutividade hidráulica da rocha
cristalina fraturada. A porosidade do
cristalino fraturado é tipicamente muito
menor que no meio poroso – Em torno de
1% comparado com 25%,
respectivamente (Freeze and Cherry,
1979).
• As fraturas das rochas influenciam
fortemente o escoamento nesta
formação.
• As equações convencionais para
poços, desenvolvidas primariamente
para aqüíferos homogêneos não são
adequadas descrever o escoamento em
rochas fraturadas.
• Uma exceção ocorre em rochas duras de
muito baixa permeabilidade se as
fraturas são numerosas o suficiente e
são uniformemente distribuídas em por
toda a rocha;
• então o escoamento que irá ocorrer
através das fraturas será similar ao que
ocorre em aqüíferos homogêneos não
consolidados.
• Um complicador na análise de testes de
bombeamento em rochas fraturadas é o
padrão das fraturas, que raramente é
conhecido com precisão.
• Precisamos encontrar, portanto um
modelo teórico bem definido para
simular o comportamento do sistema real
e produzir respostas do modo mais
próximo possível de sua resposta
observada.
Hydraulics of Fracture Flow
Lei Cúbica:
b 
h
q
bDEPTH
12
x '
2
•
•
•
•
•
•
q [L³/T] = Vazão
b [L] = Abertura das fraturas
DEPTH [L] = Profundidade
 [M/(L²T²) = Peso específico do fluido
 [M/(LT)]= Viscosidade dinâmica
dh/dx’ [L/L]= Componente do gradiente hidráulico
Condutividade Hidráulica:
2
gb
K
b
12
• g [L/T²]= Aceleração da gravidade
• b [L] = Abertura das fraturas
•  [L²/T]= Viscosidade cinemática da água 15ºC
Exemplo de
Pesquisas no Mundo
• Ground Water Flow and Transport in
Fractured Rock: (Mirror Lake, New
Hampshire)