6ºano -2014

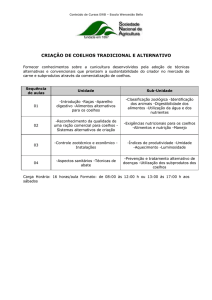
COLÉGIO INTEGRAÇÃO ANGLO
ALUNO (A):_____________________________________________________________________ TURMA: ______
8º ANO DO ENSINO FUNDAMENTAL (Tarde)
Professor:
Bachion/
Guilherme
1.
2.
3.
4.
5.
6.
7.
TR3
Atenção para os seguintes procedimentos:
Anexe esta folha ao Trabalho, pois a correção será baseada nela.
Faça, treine e deixe as resoluções no Trabalho, mas elas não terão valor de correção.
Preencha todo o cabeçalho acima.
Esta folha deverá ser resolvida somente À TINTA (azul ou preta), portanto, NÃO SERÃO aceitas marcações a lápis,
datilografados, digitados e, principalmente, rasuradas.
Aproveite este Trabalho para estudar para a recuperação, ou seja, as questões da prova serão baseadas nele e no Roteiro
estabelecido.
É NECESSÁRIA A APRESENTAÇÃO DE DOCUMENTO COM FOTO NO DIA DA PROVA
Esta folha (anexada ao Trabalho) deverá ser entregue no dia da aplicação da prova em 2015, conforme quadro abaixo:
Ensino Fundamental
06/01
07/01
08/01
1º DIA
2º DIA
3º DIA
Ensino Médio
Atitude, Ciências e Redação.
Espanhol, Inglês, Literatura e Português.
Matemática, Geografia e História.
06/01
07/01
08/01
1º DIA
2º DIA
3º DIA
Biologia, Física, Química e Redação.
Espanhol, Inglês, Literatura e Português.
Matemática, Filosofia, Geografia, História e Sociologia.
O TRABALHO SERÁ CORRIGIDO SOMENTE PELO QUADRO DE RESPOSTAS 
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20
ALTERNATIV
AS
QUESTÕES
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
ROTEIRO
Prof. Bachion








Valor: 40,0
pontos
ROTEIRO / TRABALHO RECUPERAÇÃO FINAL - MATEMÁTICA
Retas paralelas cortadas por uma transversal (ângulos)
Teorema de Tales
Soma dos ângulos internos de um triangulo
Soma dos ângulos externos de um triangulo
Soma dos ângulos internos de um polígono qualquer
Soma dos ângulos externos de um polígono qualquer
Semelhança de triângulos
Áreas (losango, paralelogramo, quadrado, triangulo,
retângulo)
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
TRABALHO
QUESTÃO 01
Determine o valor do
ângulo x da figura ao
lado.
(a)
(b)
(c)
(d)
(e)
45°
20°
30°
90°
60°
Prof. Guilherme




Análise Combinatória e probabilidade
Plano cartesiano
Sistema de equações
Polinômios
QUESTÃO 02
Utilizando a semelhança de triângulos qual o valor de x do
triangulo abaixo?
(a) 3 m
(b) 4m
3TRB8MMATEMATICA_MAR_14
(c) 2m
(d) 5m
(e) 6m
QUESTÃO 07
Abaixo temos o formato de uma tampa de alumínio utilizada
na embalagem de sardinhas, sabendo que o preço da tampa
é de R$ 0,10 o m2 quanto custara cada tampa?
QUESTÃO 03
Observe o triângulo abaixo.
(a)
(b)
(c)
(d)
(e)
O valor de x é
(a)
(b)
(c)
(d)
(e)
110°.
80°
60°.
50°.
30
R$ 2,48
R$ 2,40
R$ 20,86
R$ 24,80
R$ 2,20
QUESTÃO 08
Qual a área da seguinte figura?
QUESTÃO 04
Calcule a medida do ângulo interno e o externo do octógono
regular.
(a)
(b)
(c)
(d)
(e)
130° e 45°
135° e 45°
145° e 45°
160° e 25°
145° e 45°
QUESTÃO 05
Qual a soma dos ângulos internos de um hexágono?
(a)
(b)
(c)
(d)
(e)
600°
620°
720°
500°
120°
(a)
(b)
(c)
(d)
(e)
50 cm2
500 cm2
25 cm2
250 cm2
1000cm2
QUESTÃO 09
Qual a área da seguinte figura
QUESTÃO 06
Andressa estava à toa em casa à toa para aliviar seu tédio
resolver medir a altura de um poste, Andressa que não é
uma aluna qualquer sabia que não havia a necessidade de
subir no poste para medir a sua altura. Então Andressa que
mede 1,60 metros resolveu medir a sua sombra com o
auxilio de um trema e obteve que sua sombra mede 40cm
ou seja 0,40m. após medir a sua sombra mediu a sombra do
poste e viu que tinha um comprimento de 2m. Com isso
Andressa conclui que a altura do poste era:
(a)
(b)
(c)
(d)
(e)
6m
7m
8m
9m
10 m
3TRB8TMATEMATICA_MAR_14
(a)
(b)
(c)
(d)
(e)
1050 m2
3000 m2
1500 m2
30000m2
1100 m2
QUESTÃO 10
Qual a área da seguinte figura
(a)
(b)
(c)
(d)
(e)
2000
1000
250
500
125
QUESTÃO 11
No lançamento de dois dados honestos, não viciados,
determine o Espaço Amostral, ou seja, mostre todos os
possíveis resultados e calcule a probabilidade de que a
soma dos números obtidos seja igual a 5.
1
2
4
(b)
9
4
(c )
6
5
(d )
6
1
(e )
9
(a )
QUESTÃO 12
Sabemos que par ordenado é um ponto (x;y) o qual
localizamos num sistema de coordenadas cartesianas. Qual
dos pares ordenados abaixo pode ser solução da equação
x + y =3?
(a)
(b)
(c)
(d)
(e)
(1; 4)
(-1; -3)
(-1; 4)
(-2; 3)
(-5;2)
QUESTÃO 13
Na equação 2x –y = 6, qual o valor de x para y = 10?
(a)
(b)
(c)
(d)
(e)
-8
6
2
8
16
QUESTÃO 14
Quais as coordenadas do ponto A abaixo?
(a)
(b)
(c)
(d)
(e)
(-3; -2)
(-3; 2)
(2; -3)
(2; 3)
(-3; 3)
QUESTÃO 15
Fatorar uma expressão é transformá-la em um produto de
fatores ou monômios.
Assim, fatorar x² + xy.
(a)
(b)
(c)
(d)
(e)
x(x + y)
x³y
2xy
y( x + y)
x(1 + y)
QUESTÃO 16
Desenvolva ( 6y + 4)² . Lembre-se que você deverá ou
utilizar a fórmula do quadrado da soma de dois termos que
é igual ao quadrado do primeiro mais duas vezes o primeiro
vezes o segundo mais o quadrado do segundo, ou seja:
( a + b)² = a² + 2ab + b² ou fazer a distributiva de
( 6y + 4)(6y + 4).
(a)
(b)
(c)
(d)
(e)
6y² -24y + 16
36y² + 48y + 16
36y² + 16
12y + 8
6y² +24y + 16
QUESTÃO 17
Simplificar uma expressão algébrica é fazer as operações
necessárias para que ela se torne menor. Assim, reduzindo
os termos semelhantes da expressão algébrica dada por
(x + 2)² + (x – 2)² o resultado será igual a:
(a)
(b)
(c)
(d)
(e)
x+8
x² – 8
2x² + 8
x² + 8
2x² - 8
QUESTÃO 18
Resolva algebricamente o sistema de equações abaixo:
4 x  y  0

2x  3 y  7
(a) S={( 2; 1)}
(b) S={( -2; 1)}
(c) S={( -2;- 1)}
3TRB8TMATEMATICA_MAR_14
(d) S={( 0,5 ; 2)}
(e) S={( -0,5; -2)}
QUESTÃO 19
Num quintal há galinhas e coelhos num total de 20 animais
e 70 patas. Chame de x o número de galinhas e de y o
número de coelhos e calcule quantas galinhas e quantos
coelhos existem naquele hospital.
(a)
(b)
(c)
(d)
(e)
Há 5 galinhas e 15 coelhos
Há 15 galinhas e 5 coelhos
Há 8 galinhas e 12 coelhos
Há 7 galinhas e 13 coelhos
Há 13 galinhas e 7 coelhos
QUESTÃO 20
Resolvendo o sistema de equação a seguir obteremos, para
x e y nessa ordem:
x+y=1
4x + 7y = 10
(a)
(b)
(c)
(d)
(e)
1e2
-1 e 2
-1 e -2
0 e -14
1e5
3TRB8TMATEMATICA_MAR_14