5. Fontes do campo magnético

5. Fontes do campo magnético: campo magnético criado por uma corrente num
condutor (lei de Biot-Savart, lei de Ampère), magnetismo na matéria.
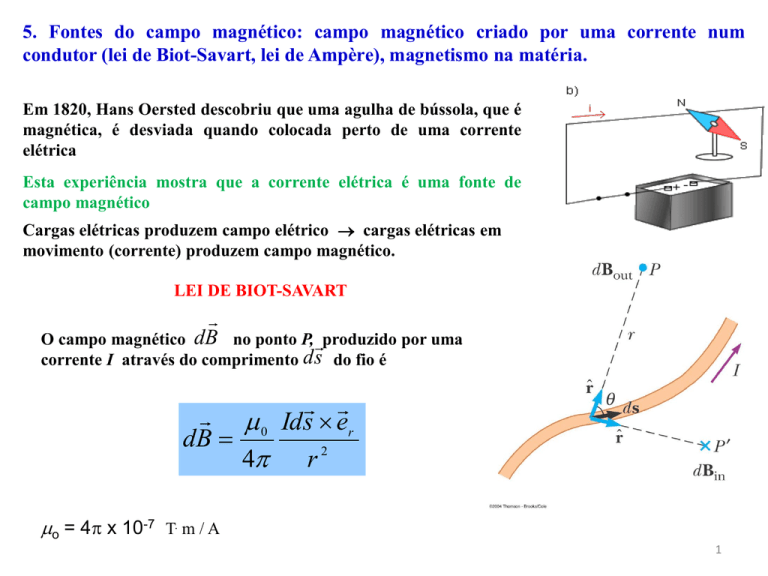
Em 1820, Hans Oersted descobriu que uma agulha de bússola, que é
magnética, é desviada quando colocada perto de uma corrente
elétrica
Esta experiência mostra que a corrente elétrica é uma fonte de
campo magnético
Cargas elétricas produzem campo elétrico  cargas elétricas em
movimento (corrente) produzem campo magnético.
LEI DE BIOT-SAVART

dB
O campo magnético
no ponto P, produzido por uma
corrente I através do comprimento d s do fio é
  0 Ids  er
dB 
4
r2
o = 4 x 10-7 T. m / A
1
O campo magnético total será

 0 I
B   dB 
4
 
ds  er
 r2
Regra da mão direita para determinar a direção do
campo magnético

Em volta de um fio longo transportando uma
corrente, as linhas do campo magnético formam
círculos em torno do fio.
Módulo do campo magnético
gerado pelo fio

B

B

B
0 I
B
2r
Linhas de campo magnético
ao redor do fio com corrente I
evidenciadas com limalhas de
ferro 
2
Em volta de um fio longo transportando uma corrente, as linhas do campo magnético formam
círculos em torno do fio.
3
FORÇA MAGNÉTICA ENTRE DOIS CONDUTORES PARALELOS

A corrente do fio 2 gera um campo magnético B2 na
posição do fio 1. B2 é perpendicular ao fio 1.
 correntes de mesmo sentido
A força magnética sobre o fio 1 é

 
F1  I1   B2
F1  I1B2
mas B2 
F1  I1(
F1 
0 I 2

2a
0 I 2
) ou
2a
 0 I 1 I 2
2a
Em termos de força magnética por unidade de comprimento
F1  0 I 1 I 2


2a
 Esta equação pode ser aplicada também a um fio de comprimento infinito
4
Supor agora que a corrente do fio 1 gera um campo magnético
perpendicular ao fio 1.

 
F2  I 2   B1 
 0 I 1 I 2
F2 
2a


 F2  F1


na
posição
do
fio
2.
é
B
B1
1
Os fios se atraem
Quando as correntes estão em direções opostas, as forças magnéticas têm sentidos opostos e os
fios se repelem
Correntes na mesma direção se atraem
Correntes em direções opostas se repelem
5
A expressão
F1  0 I 1 I 2


2a
é utilizada para definir o Ampère:
Definição do Ampère
Dois fios longos e paralelos a 1 m de distância um do outro conduzem a mesma
corrente e a força por unidade de comprimento em cada fio é
2 10 7 N/m

essa corrente é definida como sendo 1 A
Definição do Coulomb
Se um condutor conduz uma corrente de 1 A, a quantidade de carga que flui
através duma seção transversal do condutor em 1 s é 1 C.
6
LEI DE AMPÈRE
Com a lei de Gauss, que é uma
relação entre a carga elétrica e o
campo elétrico produzido por esta
carga, podíamos determinar o
campo
elétrico
em
situações
altamente simétricas .
Agora estudaremos a lei de
Ampère, que é uma relação
análoga no magnetismo  só
que é uma relação entre uma
corrente e o campo magnético
que esta corrente produz.
(a) A bússola aponta sempre
na mesma direção  norte
geográfico)
(b) a bússola

direção de B
aponta
na
 
Calculamos o produto B  ds para um pequeno
 segmento de comprimento
ds sobre a trajetória circular da Figura b. B  ds  Bds
B é constante e a soma dosprodutos
Bds sobre toda a trajetória fechada

 a integral de linha de B  ds :
 
0 I
B

d
s

B
ds


 2r (2r )   0 I
Para qualquer trajetória temos
 Lei Ampère
 
 B  ds   0 I
7
Exemplo 1: Cálculo do campo magnético criado por um fio longo que conduz uma corrente
rR
Trajetória circular 1
 
 B  ds  B  ds 
I0
B(2r )  0 I 0 
B
r<R
0 I 0
2r
Trajetória circular 2
r
I  I0
I
r 2
r 2
r2

 I
I0  2 I0
2
2
I 0 R
R
R
 
2

r
B

d
s

B
ds

B
(
2

r
)


I

0
0


I0
2
R
ou B 2r 
0 r 2
R
2
I0
0 I 0
 B
r
2
2R
8
LINHAS DE CAMPO MAGNÉTICO NUMA ESPIRA CIRCULAR

Líneas de campo
creado por una
espira circular
Linhas de campo magnético
ao redor de uma espira com
corrente I evidenciadas com
limalhas de ferro 
9
Exemplo 2: Cálculo do campo magnético criado por uma bobine toroidal
Fio condutor enrolado num anel não condutor (toro)
São N espiras, cada uma conduz uma corrente I
Campo magnético criado dentro do toro
 
 B  ds  B  ds B(2r )   0 NI
B=0 fora da bobine
 0 NI
B
2r
10
Exemplo 3: Cálculo do campo magnético de um solenoide
Um fio longo enrolado formando uma bobina em espiral é chamado de solenóide.
O campo magnético gerido por um
solenóide com as espiras mais
espaçadas.
Solenóide compacto
Imane

(a)
(b)
(c)
b) O campo no espaço interior do solenóide é intenso e quase uniforme.
11
SOLENÓIDE
12
Secção recta longitudinal
do solenóide
Solenóide ideal
O campo magnético fora do solenóide é nulo.
Para calcular o campo magnético dentro do solenóide
utilizamos a lei de Ampère considerando a trajetória
tracejada.
 
 
 
 
 
 B  ds   B  ds   B  ds   B  ds   B  ds 
1
2
3
4
 
 
 
 B  ds   B  ds  0  0  0   B  ds  B ds  B
1
 
 B  ds B   0 NI 
1
B  0
1
N
I   0 nI

13
MAGNETISMO NA MATÉRIA
Para compreender por que alguns materiais são magnéticos, é
importante
analisar
o movimento de eletrão no átomo,
considerando o modelo estrutural de Bohr.
μorb
Bohr supõe que os eletrões no átomo descrevem órbitas circulares
em torno do núcleo de massa muito maior
I
Cada eletrão numa órbita representa uma
muito pequena.
espira de corrente
I  corrente na direção convencional

  IA 

e 

L
2 me

I
e  1.6  10 9 Coulombs
me  9.11  10
31
kg
I 
e
e
ev


T
2
2r
e
A  r 2
 momento magnético associado com o movimento
do eletrão em torno do núcleo
Na maioria das substâncias,  de um eletrão num átomo é
cancelado pelo  de um outro eletrão no mesmo átomo que está
orbitando na direção oposta
 o  resultante é nulo ou muito pequeno, para a
maioria dos materiais
14
Além de seu momento angular orbital, um eletrão tem um momento angular intrínseco,
chamado SPIN, que também contribui para seu momento magnético.
e 
 S
m

O momento magnético de spin é da mesma ordem de grandeza do momento magnético orbital.
Em átomos ou iões que contêm muitos eletrões, vários desses eletrões estão emparelhados com
seus spins em direções opostas  num cancelamento dos momentos magnéticos de spin.
Para um número ímpar de spins pelo menos um eletrão estará desemparelhado  material
tem momento magnético resultante que conduz a vários tipos de comportamento magnético.
15
MATERIAIS FERROMAGNÉTICOS
Ferro, Cobalto, Níquel, Gadolínio e Disprósio são materiais fortemente magnéticos, sendo
chamados de ferromagnéticos.
São materiais usados para fabricar ímãs permanentes, contêm átomos
com momentos magnéticos de spin que tendem a se alinhar paralelos
uns aos outros, mesmo na presença dum campo magnético externo
fraco.
Uma vez que os momentos estão alinhados, a substância permanece
magnetizada mesmo após o campo externo ser removido.
Todos os materiais ferromagnéticos contêm regiões microscópicas ( 1012 até 108 m3 ),
denominadas domínios, dentro das quais todos os momentos magnéticos estão alinhados.
AMOSTRA DESMAGNETIZADA
AMOSTRA MAGNETIZADA
Quando o campo externo é removido, a amostra pode reter a maior parte de seu
magnetismo.
16
MATERIAIS NÃO FERROMAGNÉTICOS
Quando se aplica o campo magnético são induzidas pequenas correntes microscópicas
que se opõem nos seus efeitos magnéticos às variações do campo aplicado.
Comportamento DIAMAGNÉTICO  momentos magnéticos em oposição ao campo
magnético aplicado.
Supercondutores
Diamagnetismo perfeito
Comportamento PARAMAGNÉTICO, há a possibilidade de alinhar os momentos
magnéticos atómicos individuais e o campo magnético intensifica-se.
17
6. Campo elétrico devido à um campo magnético variável (Lei de Faraday)
LEI DA INDUÇÃO DE FARADAY
Aprendemos que:
Uma espira condutora percorrida por uma corrente I na presença de um campo
magnético, sofre ação de um momento da força (torque):
ESPIRA COM CORRENTE + CAMPO MAGNÉTICO = MOMENTO DA FORÇA
O que acontecerá..
se uma espira sem corrente girar no interior de uma região onde há um campo
magnético B ? Aparecerá uma corrente I na espira?
MOMENTO DA FORÇA + CAMPO MAGNÉTICO = CORRENTE ?
As resposta a essa questão foi dada por Faraday
Ele observou que o movimento relativo no conjunto
ímanes e circuitos metálicos fechados fazia aparecer
nos circuitos metálicos corrente elétricas
18
Já estudamos campos elétricos devido às cargas estacionárias e campos magnéticos devido a
cargas em movimento.
Estudaremos agora o campo elétrico devido a um campo magnético variável
EXPERIÊNCIAS REALIZADAS POR FARADAY
1ª Experiência. Considere uma espira ligada a
um galvanómetro (aparelho que mede a corrente
elétrica):
a) Quando o imane é deslocado em direção a espira o
galvanómetro indica que uma corrente é induzida na
espira.
b) Quando o imane é mantido parado
corrente é induzida na espira.
nenhuma
c) Quando o imane é afastado da espira o galvanómetro
indica que uma corrente é induzida na espira  oposta
a corrente da alínea (a)
Conclusão: uma corrente elétrica é criada num circuito
do galvanómetro enquanto ocorrer um movimento
relativo entre o imane e a espira.
Chamamos essa corrente de corrente induzida e ela é produzida por uma fem induzida
Esses resultados são notáveis pelo fato de existir corrente num fio sem que nenhuma
19
bateria esteja ligada a ele
2ª Experiência. O aparelho, ilustrado na figura, compõe-se de duas partes:
Bobine primária
Bobine secundária
• Um circuito primário que consiste de uma bobine (primária), enrolada num anel de ferro, ligada
a uma chave e a uma bateria;
• Um circuito secundário que consiste de uma bobine (secundária), enrolada num anel de ferro e
ligada a um galvanómetro
Quando a chave do circuito primário é fechado, o galvanómetro no circuito secundário se desvia
momentaneamente.
A fem induzida no circuito secundário é causada pelo campo magnético variável através da bobine
secundária.
Nesta experiência, uma fem é induzida na espira somente quando o campo magnético que a
atravessa estiver variando.
Faraday concluiu que uma corrente elétrica pode ser produzida por um campo
magnético variável
20
FLUXO MAGNÉTICO
Para quantificar essas observações, temos de definir uma nova grandeza, o fluxo magnético.
A definição é similar a definição de fluxo elétrico
O fluxo associado com um campo magnético é proporcional ao número de linhas do campo
magnético que atravessam uma área.
O fluxo magnético através um plano de área
A que faz um ângulo θ em relação ao campo
magnético uniforme é
 
 B  B  A  BAcos
O fluxo magnético total que atravessa a
superfície aberta arbitrária é
a)  B  BA cos 90  0
b)  B  BA cos 0  BA
 
 B   B  dA
A unidade SI do fluxo magnético chama-se weber (Wb)
1 Wb  1 T m2
21
A LEI DE FARADAY DA INDUÇÃO
Uma fem é induzida num circuito quando o fluxo magnético através da superfície limitada pelo
circuito varia com o tempo.
A fem induzida num circuito é igual à taxa temporal de variação do fluxo magnético através do
circuito.
Esse enunciado é conhecido como lei de Faraday da indução.
d B
 
dt
 B  fluxo magnético através da superfície limitada pelo circuito
Discutiremos depois o sinal negativo
Se o circuito for uma bobine de N espiras idênticas concêntricas e se as linhas do campo
atravessarem todas as espiras , a fem induzida será:
d B
  N
dt
22
O fluxo magnético através da espira é
 
 B   B  dA  BdA cos  B cos  dA  BA cos
Logo a força eletromotriz induzida
d B
 
dt
 
d
( BA cos )
dt
Então, uma fem pode ser induzida num circuito variando-se o fluxo magnético de diversas
maneiras:
1. Variar o módulo de B com o tempo.
2. Variar a área A do circuito com o tempo.
3. Variar o ângulo θ entre B e a área com o tempo.
4. Qualquer combinação dessas três variações.
23
A LEI DE LENZ
A direção da força eletromotriz induzida e da corrente são determinados pela Lei de Lentz
O sentido da corrente induzida é tal que o campo magnético devido a ela se opõe à variação do
fluxo magnético que a produziu.
Oposição ao movimento do imane  Oposição à variação do fluxo magnético
(a)
(b)
d B
 
dt
a) Quando o imane é deslocado em
direção à espira condutora
parada, uma corrente I é induzida
na espira
b) I produz o seu próprio campo
magnético, que se opõe ao fluxo
externo crescente
c) Quando o imane afasta-se da
espira condutora parada, uma
corrente I é induzida na espira
d) I produz o seu próprio campo
magnético, que se opõe ao fluxo
externo decrescente
(c)
(d)
24