Capitulo - 3 - Eq Kelvin-Kohler - storm-t

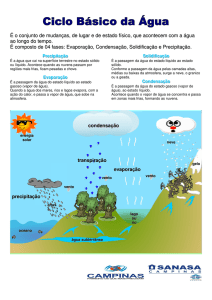
Formação de Gotas de Nuvem
a) Aspectos gerais da formação de nuvens e precipitação:
As mudanças de fase da água são os principais processos de
interesse em microfísica de nuvens. Sendo que das possíveis
mudanças de fase temos:
Vapor
 Liquido
{ condensação/evaporação }
Liquido
 Solido
{ fusão/derretimento }
Vapor
 Solido
{ deposição/sublimação }
As mudanças que ocorrem da esquerda para direita,
exemplo Vapor  Liquido, Vapor  Sólido e
Líquido  Sólido
correspondem a um crescimento de ordem molecular.
Como visto anteriormente, estas mudanças não ocorrem em
equilíbrio termodinâmico, mas na presença de uma barreira
de energia livre forte.
Gotas de água, por exemplo, são caracterizadas por uma força
de tensão superficial grande. Para as gotas se formarem por
condensação a partir do vapor, a tensão superficial deve exceder
o forte gradiente da pressão de vapor.
A equação de Clausius-Clapeyron descreve a condição de
equilíbrio para um sistema termodinâmico que consiste de água e
vapor.
A saturação é definida como a situação de equilíbrio no qual as
taxas de evaporação e condensação são iguais.
Entretanto, para gotas pequenas onde a barreira de energia livre
é alta, a fase de transição não ocorre geralmente no equilíbrio de
saturação da água. Em outras palavras, se uma amostra de ar
úmido for esfriado adiabaticamente ao ponto de equilíbrio de
saturação da água, não deve-se esperar a formação de gotas.
Na verdade, as gotas de água começam a condensar a partir
do vapor de água pura somente quando a umidade relativa
alcançar algumas centenas de por cento (>>100%) !!!!!
Porque as gotas de nuvem se formam na atmosfera quando o ar
ascendido atinge o equilíbrio de saturação (NCC e NCL)?
Por causa da presença de partículas (aerossóis) de tamanho de
mícron e sub-mícron que tem afinidade com a água servem como
centros de condensação. Estas partículas são chamadas de
núcleos de condensação (CCN).
• O processo no qual as gotas de água se formam em
núcleos de condensação a partir da fase vapor é
conhecido como nucleação heterogênea.
• A formação de gotas a partir do vapor em um ambiente
puro (sem aerossóis) é conhecido como nucleação
homogênea e requer um super-saturação extremamente
alta.
• Todos os processos onde a barreira de energia livre
deve ser superada, tais como as transições do vapor
para o liquido ou do liquido para o gelo são definidas
como processos de nucleação.
Diferentes tipos de CCN estão presentes na atmosfera. Alguns
tornam-se molhados a UR < 100% e estão associados aos
nevoeiros.
CCNs relativamente grandes podem crescer a tamanhos de gotas
de nuvem. A medida que o ar úmido é esfriado em levantamento
adiabático, a UR se aproxima dos 100%. Então a presença de
mais partículas higroscópicas (afinidade com a água) começa a
servir de centros de condensação. Se o levantamento do ar
úmido continuar, a super-saturação será produzida pelo
esfriamento e será usada pela condensação no núcleo de
condensação.
Sendo que a super-saturação é quando a umidade relativa
excede o valor de equilíbrio de 100%. Então o ar com uma
umidade relativa de 101.5% terá uma super-saturação de 1.5.
Nas nuvens, existem núcleos suficientes que não deixam a supersaturação crescer a valores acima de 1%. Uma das
características importantes da atmosfera, é que existem núcleos
de condensação suficiente para produzir a formação de nuvens
quando a umidade relativa exceder um mínimo de 100%.
Se uma nuvem continuar a ascende e o seu topo atingir
temperaturas inferiores a 0oC, o o vapor começa a sublimar sobre
núcleos de gelo (IC) e cristais de gelo se formam, já as gotículas
de água começam a se congelar.
As gotículas de água que não se congelam são chamadas de
“gotas super-resfriadas”, e podem ou não se congelar a medida
que Temperatura da nuvem diminui.
Para gotas de água pura, o congelamento homogêneo ocorrerá
somente quando a temperatura atingir –40oC.
Entretanto, quando um número razoável de núcleos de gelo
estiver presente na nuvem, o congelamento pode ocorrer a
alguns graus abaixo de zero.
Apesar de que estes aerossóis não sejam completamente
conhecidos, eles são significativamente escassos na atmosfera,
quando comparados com os CCN. Conseqüentemente a supersaturação de alguns décimos são extremamente incomuns na
atmosfera, apesar das gotículas de água super-resfriadas são um
estado regular de afinamento.
O super-resfriamento abaixo de –15oC não são tão comuns. Por
esta razão um dos métodos mais comuns para a modificação
artificial de nuvens é a da adição de núcleos de gelo (IC).
Uma nuvem é composta de gotas bem pequenas, usualmente
com uma concentração de várias centenas por centímetro cúbico
e com raio de ~ 10 m.
Esta estrutura é extremamente estável; ou seja, as gotas
mostram pequena tendência para ficarem juntas ou para
mudarem seus tamanhos exceto pelo crescimento geral de uma
população em geral.
A precipitação se desenvolve quando a população de
gotículas de nuvens torna-se instável, e conseqüentemente
algumas gotículas crescem partir do custo das outras.
Existem dois mecanismos os quais a micro-estrutura da
nuvem pode ser instável:
A primeira é a colisão direta e ou seguida de coalescência (se
juntam) de gotas de água e podem ser importantes em
qualquer nuvem.
O segundo mecanismo requer a interação entre gotas de
água e cristais de gelo e está confinado à nuvens que tem
topos que excedem temperaturas inferiores à 0oC.
A partir da análise de forças aerodinâmicas foi encontrado que
gotas pequenas não podem fazer a colisão.
Uma gota pequena caindo dentro de uma nuvem com gotas mais
pequenas ainda, irá colidir com uma fração de minuto das gotas
que estão no seu caminho se o raio é menor que ~ 18 m.
Portanto, nuvens que possuam concentrações negligenciáveis
de gotas maiores que 18 m estarão relativamente estáveis
em relação ao crescimento por coalescência.
Já Nuvens com números consideráveis de gotas grandes
podem desenvolver precipitação.
Quando cristais de gelo existem na presença de um grande
número de gotas de água super-resfriadas a situação é
imediatamente instável.
A pressão de vapor de equilíbrio sobre o gelo é menor que
sobre a água sob a mesma temperatura e
conseqüentemente os cristais de gelo crescem por
difusão do vapor e as gotas evaporam para compensar.
A transferência de vapor depende da diferença entre a pressão
de vapor de equilíbrio da água e do gelo e é mais eficiente com
temperaturas ~ -15oC.
Uma vez que os cristais de gelo cresceram por difusão a
tamanhos apreciáveis e maiores que as gotículas de água, eles
começam a cair relativamente em relação a elas e colisões
tornam-se possíveis.
Se as colisões são basicamente entre cristais de gelo, flocos de
neve se formam. Se gotas de água são coletadas, pedras de
gelo pequeno ou granizo podem se formar.
Uma vez que as partículas caem abaixo da isoterma de 0oC, o
derretimento pode ocorrer e as partículas que emergem a partir
da base da nuvem como gotas de chuva são indistinguíveis das
que foram formadas por coalescência.
Em condições meteorológicas frias, ou quando grandes pedras
de granizo são formadas, estas partículas podem atingir o chão
sem se derreter.
Dimensão das Partículas
b) Nucleação da água liquida a partir do vapor de água
O grande problema da nucleação consiste em responder a
seguinte pergunta:
Qual é a chance real de colisões e agregações de moléculas de água
levar a formação de gotas embriônicas que estejam estáveis e
continuem a existir sob uma dada condição ambiente?
A gota embriônica estará estável se o tamanho exceder um valor
crítico. Na média, as gotas maiores que um tamanho critico
crescerão, enquanto que as menores irão diminuir.
O que determina o tamanho critico é o balanço entre as taxas
opostas de crescimento e decaimento. Estas taxas, dependem se
a gota se forma em um espaço livre (nucleação homogênea) ou
em contacto com outro corpo (nucleação heterogênea).
Para a nucleação homogênea de água pura, a taxa de
crescimento depende da pressão parcial do vapor d’água nas
vizinhanças, porque isso determina a taxa a qual as moléculas de
água se aglutinam na gota.
O processo de decaimento, ou seja a evaporação, depende
altamente da temperatura da gota e a sua respectiva tensão
superficial. As moléculas na superfície da gota, devem ter energia
suficientemente grande para exceder as forças que as aglutinam
caso elas tendam a escapar.
Se o equilíbrio é estabelecido entre o liquido e o vapor, as taxas
de condensação e evaporação são exatamente balanceadas e a
pressão de vapor é igual ao do equilíbrio ou o da pressão de
vapor de saturação.
A pressão de vapor de equilíbrio sobre a superfície de uma gota
depende da sua curvatura, e quanto maior for a gotícula ou a área
superficial menor será a pressão de vapor necessária para
condensar.
Por exemplo, é possível observar a formação de gotas sobre os
azulejos, espelhos e ou superfícies planas em ambientes
extremamente saturados.
Este processo foi derivado por por William Thomson (se tornando
mais tarde o Lord Kelvin) em 1870, quando tentava explicar a
subida dos líquidos em tubos capilares.
Como existe uma mudança de fase (vapor liquido) para
formar uma gotícula, podemos avaliar a variação da
Função de Gibbs sobre uma gotícula.
Lembrando que a Função de Gibbs é dada por:
g = u + p - T,
Temos que em uma condição de equilíbrio entre o
vapor (2) e o liquido (1) era que:
g1=g2
Porém durante a mudança de fase, temos um processo
não-isotérmico e não-isobárico, logo.
dg = du - Td - dT + pd + dp
lembrando da 1a e 2a lei da termodinâmica
1º dq = du - pd
2º dq = Td
dg = dp - dT
Suponha agora que para um sistema composto por uma gotícula
de água líquida em equilíbrio com o vapor, ocorra uma
mudança de fase através de um processo isotérmico. Durante
esta mudança de fase, esta gotícula de água irá crescer de um
tamanho “r” a um “r + dr” e conseqüentemente a sua pressão de
vapor de equilíbrio “ec” irá aumentar para “ec + dec”.
Lembrando que para um processo reversível temos que:
g1  g1 + dg1
g2  g2 + dg2
mas como g1 = g2  dg1 = dg2
Logo temos as seguintes variações da função de Gibbs:
Vapor:
dg2 2de
c
Gotícula de água:
ecP
dg

d
1
1
i
onde Pi é a pressão interna de uma gotícula de água com
raio “r” e é definida como:
2
Pi 
r
 é a tensão superficial e para a água a uma T=0 oC
 = 75 dynes x cm-1 ou 7,5x10-2 N/m.
A tensão superficial é a energia livre por unidade de área
superficial do líquido e ou o trabalho (por unidade de área)
necessário para expandir a área do liquido a uma
temperatura constante.
Dessa maneira, re-escrevendo a Função de Gibbs para a
gotícula de água, temos:



dr
2



dg
=
d
e
+
P
=
de


1 1 c i
1
c
2
 r
Como a variação da função de Gibbs do vapor é igual à da
água temos:

dr
 2


de


de

1
c- 2 
2
c
r

2

dr




de

2
1
c
1 2
r
Lembrando que o volume específico do vapor é muito maior
que o do liquido (2>>1),
e que 2 = 1/v e 1 = 1/L (densidade do vapor e líquido)
2 = RvT/ec
2
2

dr
de
- 2
c

r
1
2

dr

de
- 2
2
L
c
r
de
2

dr
c


2
e
R
T

c
V
Lr
Integrando desde a superfície do plano até sob a gota temos:
es  esc
r=  r=R (ou seja, plano a gota)
de
2

dr
c


2


e
RvT

r
c
L
e

s
e
(
R
)
sc
R
Logo a Equação de Kelvin é:
2


e
(
r
)
e


sc
sexp
R
T

r
V
L


lembrando que S = esc/es  Super-saturação
esc/es
1
1.012
1.120
~3
R(m)
a T=273 oK
0.1
0.01
0.001  UR não encontrada na atmosfera
De um forma mais genérica a pressão de vapor de equilíbrio
sobre a superfície de uma gota poder ser expressa como:
2


e
(
r
)

e
(

)
exp


s
s
rR

T
v
L


Equação de Kelvin
Note que a medida que o raio da gota diminui, a pressão de
vapor necessária para o equilíbrio aumenta.
A taxa de crescimento resultante de uma gota com raio “r” é
proporcional à diferença entre a pressão de vapor do ambiente e
pressão de vapor de saturação sobre a superfície de uma gota
esférica de raio “r” , ou seja, e– es(r):
e – es(r) < 0
 diminui
e – es(r) > 0
 aumenta (cresce)
Conseqüentemente, podemos determinar qual é o raio
critico (rc) que uma gotícula irá crescer em função da
Saturação do ambiente:
Para isso ocorrer temos que e – es(rc)=0
 2 
es (r) e es ()exp


rcRvLT
e
S
es ()
 2 
S exp


rcRvLT
2

rc 
R
Tln
S
v
L
2

rc 
R
Tln
S
v
L
Lembrando que S = e/ es() é a razão de saturação.
Para que uma gotícula de água formada a partir das
colisões entre as moléculas de água fique estável, ela deve
crescer a uma raio maior que rc.
A tabela acima mostra que são necessárias altas supersaturações para que pequenas gotículas se tornem estáveis. Por
exemplo, quando a super-saturação é de 1%, S = 1.01, as gotas
com raio menor que 0.121 m são instáveis e tenderão a
evaporar.
Em nucleação homogênea, gotas de tamanho critico são
formadas por colisões aleatórias das moléculas de água.
Se estas gotas capturam outra molécula, elas se tornam supercriticas; ou seja:
em aumentando o tamanho, es(r) diminui e a taxa de crescimento,
a qual é proporcional à e – es(r), aumenta.
Gotas super-críticas crescem espontaneamente.
A taxa de nucleação é simplesmente a taxa a qual as gotas
super-críticas são formadas e é dado pelo produto da
concentração de gotas críticas e taxa a qual a gota crítica ganha
outra molécula e torna-se super-critica.
A partir da termodinâmica estatística a taxa de nucleação por
unidade de volume pode ser expresso aproximadamente por:



2


4
r
e
2
c
J

4
r
Z
exp
 

c
n
3
kT
2
mkT


onde “m” é a massa da molécula de água, “k” é constante de
Boltzmann, e “n” é o número de densidade de moléculas de
vapor. O Fator “Z” é o fator de Zeldovich ou de não equilíbrio,
e é da ~ de 10-2 em unidade de CGS.
Por convenção, uma taxa de nucleação homogênea significativa é
da ordem 1 cm-3 s-1. e é denominado de razão de saturação crítica
Sc.
Teoria e dados experimentais mostram que Sc diminui com o
aumento da temperatura, e tem um valor de
~ 4.3 a 273 K,
6.3 a 250 K, e
3.5 a 290 K.
Tais valores de S não são nunca observados na atmosfera, aonde
a super-S raramente excede 1 ou 2%.
Logo : Nucleação homogênea de água liquida a partir do vapor
não é possível nestas condições.
Na atmosfera, as gotículas de nuvem se formam em aerossóis
chamados de núcleos de condensação ou núcleos higroscópicos
(CCN).
A taxa de formação de gotículas é determinado pelo número
destes núcleos presentes, e não pela colisão estatística.
Em geral, os aerossóis podem ser classificados de acordo com a
sua afinidade com a água como: higroscópicos, neutros e
hidrofóbicos.
Nucleação em aerossóis neutros requer a mesma supersaturação que uma nucleação homogênea.
Em aerossóis hidrofóbicos, os quais resistem ao
molhamento, a nucleação é mais difícil e requer valores
mais altos de super-saturação.
Mas para partículas higroscópicas, as quais são solúveis e
tem afinidade com a água, a super-saturação necessária
para a formação das gotículas pode ser bem menor que
os valores para nucleação homogênea.
Sabe-se que uma substância não volátil dissolvida no líquido,
tende a diminuir a pressão de vapor de equilíbrio do liquido.
De uma maneira geral, o efeito pode ser pensado como: “Quando
soluto é adicionado ao liquido, algumas moléculas do liquido que
estavam na camada superficial são substituídas pelas moléculas
do soluto. Logo, se a pressão de vapor do soluto é menor que a
do solvente, a pressão de vapor será reduzida na proporção da
quantidade de soluto presente”.
Portanto, este efeito pode reduzir drasticamente a pressão de
vapor de equilíbrio sobre a gota;
Como resultado, a gota da solução pode estar em equilíbrio
com o ambiente a um super-saturação bem menor que a da
gota de água pura de um mesmo tamanho.
Efeito de Aerossóis/Soluto
Efeito do Soluto
Eq. de Kohler
Avaliando este efeito
Considerar uma substância de pressão parcial
de vapor igual a zero (soluto) sendo
dissolvida em água (solvente).
Se as moléculas do soluto se distribuem
uniformemente através da água, então
algumas delas estarão posicionadas na
camada superficial, reduzindo assim a área
da superfície ocupada pelas moléculas de
água.
Portanto, a fração da área total que fica ocupada
por moléculas de água pode ser definida como:
na
xa 
na ns
onde na é o número de moléculas de água e ns é
numero de moléculas do soluto.
Neste sentido, a razão entre a pressão parcial de
vapor d’água de equilíbrio (saturação) para duas
gotículas (de mesmo tamanho), sendo uma
constituida de uma solução e a outra de água
pura, mantem a proporção de xa. .
er
xa 
esc
Onde er é a pressão parcial do vapor d’água de equilíbrio sobre a solução
aquosa e esc é a pressão parcial de vapor d’água de equilíbrio sobre superfície
de água pura.
er
na

esc na ns
Esta expressão define a Lei de Raoult para uma solução
ideal que é comumente enunciada como: A pressão parcial
de vapor de um componente na solução líquida é
proporcional à fração molar daquele componente
multiplicado pela sua pressão de vapor quando puro.
Manipulando as equações e lembrando que alguns íons
se dissociam (i = número de íons dissociados) durante o
processo, temos que:
3
im
e
sM
r

1
 3 a
e
4

r
M
sc
a
s
Ma = massa de um mol de água
Ms = massa de um mol de soluto
ms = massa do soluto
r = raio da gotícula
Esta equação mostra que pressão de vapor de saturação
d’água sobre a solução diminui rapidamente com o
decréscimo do raio da gota quando um soluto de massa ms
é dissolvido em uma gotícula de água pura.
Isso implica que uma gotícula de água constituída de uma
solução estará em equilíbrio com o meio a uma pressão de
saturação bem inferior à aquela de uma gotícula de água
pura com mesmo tamanho.
3im
sM
a
b
4
LM
s
er
b
1 3
esc
r
Da Eq. de Kelvin, temos
2
a
RVTL
a


e
(r
)
e

sc
sexp
r

Combinando então os dois efeitos:
água pura + soluto
e
(
r
)e
a

 b

sc
r

1

1





3
e
(
r
) r

r

s e
sc
ab
negligenci
ando
, 4
0
r
er
a b
1  3
es
r r
Eq. de Kohler
Curvatura
Soluto
er
a b
1  3
es
r r
Esta expressão
mostra os efeitos
da tensão
superficial
(curvatura) e das
substâncias
higroscópicas
(soluto).
Raio Critico
 e r  dS
  
 e s  dr
d 
a b
1   3
dr 
r r
d
dr
r 
*
3b
a
S 1
*
 0

 0

S*
r*
4a3
27 b