Sistemas de Numeração Importantes na Computação

Capítulo
DOIS
Sistemas de numeração em computação
2 . 1 Introdução
Em todas as fórmulas usadas a seguir, ‘B’ representa a base do sistema de numeração, ‘n’
representa a quantidade de dígitos disponíveis para representar os números, e ‘a’, ‘b’ e ‘c’
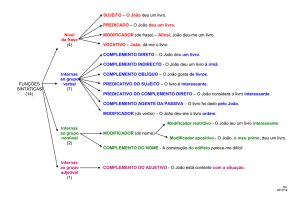
representam números. A fórmula utilizada para representar um número inteiro:
n-1
Σ (xi.B i)
a=
i=0
será representada por a=Σ n-1xiBi, ficando a variação de i desde 0 até o limite (n-1) implícita.
Para uma determinada base B, empregando-se n dígitos, pode-se representar Bn combinações distintas, ou seja, Bn números distintos. Assim, para base decimal com três dígitos
pode-se representar 1000 números distintos (com zero incluído!). Entretanto, com os
mesmos três dígitos e base dois, representa-se somente 8 números distintos. Assim,
números binários vão exigir um grande número de dígitos, e normalmente trabalha-se com
grandes cadeias de zeros e uns. Isto pode levar a erros visuais, e por isso empregam-se
comumente as notações em base 8 e base 16 para representar números binários.
A tabela abaixo lista os primeiros 16 números em binário, decimal, octal e hexadecimal.
Binário
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
Decimal
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Octal
00
01
02
03
04
05
06
07
10
11
12
13
14
15
16
17
Hexadecimal
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
Tabela 2.1 - Números em binário, decimal, octal e hexadecimal
Em computação trabalha-se normalmente com quatro bases: a decimal, para entrada e saída
dos dados (já que nossa sociedade é baseada no sistema decimal); a binária, para os cálculos
internos; a hexadecimal, como forma compactada de representação interna; e a octal, também
por este motivo. Note-se que a escolha das bases 8 e 16 não é ocasional: as transformações
2-1
entres as bases 2, 8 e 16 pode ser feita facilmente pelo método da substituição direta. Embora
a base hexadecimal seja de representação mais complexa (utiliza letras e dígitos), ela é
preferida sobre a base octal por ser mais compacta, ou seja, requerer menos espaço para
representar os resultados.
Os números do sistema binário são formados como qualquer outro número do sistema de
numeração arábico (inclusive em octal ou hexadecimal): cada novo número é obtido por
enumeração, somando-se um ao seu antecessor (e observando-se a regra do “vai-um”).
Cada dígito do sistema binário (0 e 1) é denominado de bit, a contração de binary digit. A
determinados conjuntos de bits são empregados nomes específicos. Assim, um quarteto (4
bits) é frequentemente denominado de nibble, e um octeto (8 bits) recebe a denominação de
byte (ou o termo aportuguesado baite). Os múltiplos deste conjuntos utilizam os mesmos
denominadores que no sistema decimal (K para kilo, M para Mega, G para giga, T para
3
10
Tera, P para Peta), mas o fator multiplicativo não é 1000 (10 ) mas sim 1024 (2 ). Assim,
um kilobit (abreviado 1Kb) são 1024 bits, e um kilobyte (abreviado 1KB) são 1024 bytes.
Um megabyte (1MB) são 1024 KB; um gigabyte (1GB) são 1024 MB, um terabyte (1TB)
são 1024 GB e assim por diante.
2 . 2 Soma de números binários
A soma de dois números binários utiliza as mesmas regras da soma no sistema decimal.
Como existem entretanto somente dois símbolos, a tabela de soma é extremamente simples:
a
0
0
1
1
c
0
1
0
1
d=a+c
0
1
1
0 e “vai-um”
Tabela 2.2 - Tabela verdade de um meio-somador (half adder)
Observe-se que soma de 1 mais 1 resulta em 10 (dois), ou seja, o dígito do resultado é zero e
existe a ocorrência de um “vai-um” (carry out, em inglês). Considerando-se a possível
existência de um “vem-um” (carry in) e de “vai-um” (carry out), obtém-se a tabela a seguir.
a
0
0
0
0
1
1
1
1
c
0
0
1
1
0
0
1
1
vem-um
0
1
0
1
0
1
0
1
d=a+c
0
1
1
0
1
0
0
1
vai-um
0
0
0
1
0
1
1
1
Tabela 2.3 - Tabela verdade de um somador completo (full adder)
2 . 3 Representação de números
A representação de números inteiros positivos é direta e imediata. Entretanto, é necessário
expandir (ou modificar) esta representação para incluir também números negativos. Diversas
representações foram desenvolvidas com este propósito. Quatro destas representações, as
mais comuns atualmente, são analisadas a seguir: inteiros positivos, sinal/magnitude,
complemento de B-1 e complemento de B.
2-2
2 . 3 . 1 Números inteiros positivos
Considerando-se somente a representação de números inteiros positivos, com n dígitos
pode-se representar Bn números, dispostos no intervalo fechado entre zero (o menor) e Bn–1
(o maior).
Faixa de representação: [ 0 , Bn–1 ]
Assim, para 2 dígitos decimais tem-se 100 números, de 0 a 99; para 3 dígitos em base 3 temse 27 números, de 0 (0003) a 26 (222 3); para 4 dígitos binários tem-se 24=16 números,
desde zero (00002) até 15 (11112); para 8 dígitos binários tem-se 28=256 números, desde
zero (000000002) até 255 (111111112); Não existe previsão para números negativos.
Cálculo do valor do número
O valor de número positivo é calculado pelo polinômio Σ n-1xiBi, exatamente o mesmo
método utilizado para a conversão pelo método polinomial.
Troca de sinal
Como não existe a capacidade de representar números negativos, não existe tal função.
Soma de dois números
A soma de dois números positivos é realizada somando-se os dois polinômios dígito a
dígito, de acordo com as tabelas da soma na base em questão. Para base 2 utiliza-se a Tabela
2.3 da seção 2.2. Naturalmente, nesta soma leva-se em conta os eventuais “vai-um” e “vemum”.
2 . 3 . 2 Números com sinal: representação em sinal-magnitude
Para permitir números com sinal, esta representação utiliza um dígito (normalmente o mais
significativo) para representar o sinal. No sistema decimal, o símbolo ‘–’ é usado para
indicar números negativos e ‘+’ (ou simplesmente um espaço vazio) para números positivos.
Com isto ganha-se a possibilidade de representar inteiros negativos, mas a faixa de
representação é reduzida porque tem-se agora somente (n–1) dígitos para representar a
magnitude.
Faixa de representação: [ –(Bn-1–1) , +(Bn-1–1) ] ou [ –(Bn-1–1) , (Bn-1–1) ]
Divide-se a gama de representação em dois subconjuntos simétricos, um para números
negativos e outro para positivos. A faixa dos números positivos é reduzida de um fator igual
a base B. Por exemplo, para base decimal com dois dígitos, se consideramos somente
números positivos tem-se a faixa de 0 até 99; com a representação em sinal magnitude
obtém-se a faixa de –9 até +9. Além disto, existem duas representações para o zero: –0 e +0.
De um modo geral, para uma base qualquer, das Bn combinações possíveis usam-se somente
2.B n-1–1 (descontando-se o duplo zero). No exemplo acima, das 100 combinações são
utilizadas somente 19.
Em binário, entretanto, com B=2, obtém-se 2.2n-1–1, ou seja, 2n–1 (isto é, Bn–1). Assim,
somente uma representação é perdida (a do duplo zero). Obs.: no sistema binário costuma-se
utilizar ‘1’ no lugar de ‘–’, e ‘0’ no lugar de ‘+’. Assim, para 4 dígitos, 0111 representa 7,
1111 representa –7, 0000 representa zero e 1000 representa –0.
2-3
Cálculo do valor do número
Um número em sinal magnitude, independente de qual a base utilizada, é formado por duas
parcelas, escritas lado a lado. A parcela à esquerda (S(a)) representa o sinal e a parcela à
direita (M(a)) a magnitude:
a = S(a)M(a)
onde S(a) é ‘+’ ou ‘–’, e M(a)=Σ n-2xiBi. Em binário, utiliza-se usualmente ‘0’ no lugar de
‘+’ e ‘1’ ao invés de ‘-’.
Troca de sinal
Para trocar o sinal de um número ‘a’ em sinal magnitude, troca-se simplesmente S(a),
mantendo-se a magnitude M(a). Assim, no caso de c=–a, tem-se M(c)=M(a), e se S(a)=‘+’,
então S(c)=‘–’, e se S(a)=‘–’ então S(c)=‘+’.
Soma de dois números
A soma de dois números em sinal magnitude é realizada de acordo com as regras da tabela
abaixo. No caso, deseja-se calcular d=a+c.
S(a)
+
–
+
S(c)
+
–
–
–
+
S(d)
+
–
se M(a)≥M(c), +
se M(a)<M(c), –
se M(a)>M(c), –
se M(a)≤M(c), +
M(d)
M(a)+M(c)
M(a)+M(c)
M(a)–M(c)
M(c)–M(a)
M(a)–M(c)
M(c)–M(a)
Exemplo
5 + 7 = 12
-5 + -7 = -12
7 + -5 = 2
5 + -7 = -2
-7 + 5 = -2
-5 + 7 = 2
Tabela 2.4 - Soma em sinal / magnitude
Note-se que, para realizar somas de números em sinal/magnitude, deve-se conhecer as
tabelas de soma e de subtração da base em que se estiver trabalhando. Esta necessidade de
realizar duas operações distintas (soma e subtração) torna muito mais complexa a
manipulação de números em sinal/magnitude pelo computador. Assim, apesar de familiar ao
ser humano, esta notação é pouco utilizada em computação.
Para resolver o problema de representação de números negativos, optou-se por usar a
notação em complemento da base, como visto a seguir. Duas notações foram desenvolvidas:
em complemento de (B-1) e em complemento de B Observação: a tabela de subtração em
binário será vista mais adiante (seção 2.5).
2 . 3 . 3 Números com sinal: representação em complemento de (B–1)
Para permitir que a operação de soma seja realizada de forma única, sem preocupação com os
sinais dos operandos, é utilizada a representação em complemento. Números positivos são
representados na forma normal, e números negativos são representados em complemento.
Na representação em complemento de (B-1), o complemento de um número a é obtido
subtraindo-se este número da maior quantidade representável, ou seja, Bn–1–a. Assim, na
base 10, com 3 dígitos, o complemento de 9 (10-1) de um número a é obtido pela fórmula
999-a. Note-se que isto equivale a subtrair cada um dos dígitos de a de 9, que é justamente a
base 10 menos um. Generalizando, para representar números negativos em complemento de
B–1, cada algarismo xi é complementado individualmente pela fórmula B–1–xi. A tabela a
seguir ilustra o cálculo do complemento para diversas bases.
2-4
Algarismo
0
1
2
3
4
5
6
7
8
9
B=2
1
0
-
B=3
2
1
0
-
B=4
3
2
1
0
-
B=8
7
6
5
4
3
2
1
0
-
B=9
8
7
6
5
4
3
2
1
0
-
B=10
9
8
7
6
5
4
3
2
1
0
Tabela 2.5 - Exemplos de cálculo de complemento de B-1
A notação em complemento elimina a necessidade de representação explícita do símbolo do
sinal, ou seja, não existe um símbolo especial para o sinal. A faixa de números
representáveis é dividida em duas. Uma das faixas representa números positivos, e a outra
faixa representa números negativos. Existindo m representações, as primeiras m/2 são
utilizadas para números positivos (de 0 a m/2), e as m/2 representações seguintes (de m/2 até
m) são utilizadas para números negativos. A faixa de representação fica:
Faixa de representação, para B par:
[ –(Bn/2–1) , +(B n/2–1) ]
Faixa de representação, para B ímpar:
[ –(Bn–3)/2 , +(B n–1)/2 ]
A tabela a seguir ilustra as faixas para diversas bases. Note-se que a gama de representação é
dividida em dois subconjuntos, um para números negativos e outro para positivos. A faixa
dos números positivos é reduzida da metade (em relação aos inteiros positivos). Continua
existindo a dupla representação do zero, assim como em sinal magnitude, mas não existe
mais a perda de capacidade de representação devido a existência do dígito de sinal.
Base Num.dig.
Faixa
Faixa em decimal
2
4
1000,1001,..,1111,0000,0001,..,0111
–7,–6,..,–0,+0,1,..7
3
3
112,120,121,..,222,000,001,..,111 –12,–11,–10,..,–0,+0,1,..,13
4
3
200,201,..,333,000,001,..,132,133
–31,–30,..,–0,+0,1,..31
8
3
400,401,..,777,000,001,..,376,377
–255,–254,..,–0,+0,..,255
9
2
45,46,..,88,00,01,..,43,44
–39,–38,..,–0,+0,1,..,39,40
10
2
50,51,..,98,99,00,01,..,48,49
–49,–48,..,–1,–0,+0,..,48,49
Tabela 2.6 - Exemplos de faixas de representação em complemento de B-1
Por exemplo, para base decimal com dois dígitos, se consideramos somente números positivos tem-se a faixa de 0 até 99; com a representação em complemento de 9 obtém-se a faixa
de 50 a 99 e 0 a 49. A primeira metade (de 50 a 99) representa números negativos (de –49 a
–0); a segunda metade (de 0 a 49) representa números positivos. Note-se que um número
iniciando por 9, 8, 7, 6 ou 5 é negativo; iniciando por 0, 1, 2, 3 ou 4 é positivo. Em binário,
para 4 dígitos, tem-se a faixa 1000 a 1111 (–7 a –0) e 0000 a 0111 (0 a 7). Números
iniciando por 1 são negativos, e iniciando por 0 são positivos.
Para bases ímpares, existe um número positivo a mais, e para a determinação do sinal não
basta a verificação do dígito mais significativo (veja-se a seguir). Por exemplo, na tabela 2.6,
os números em base 3 iniciando por zero são positivos, e os números iniciando por 2 são
negativos, mas dos números iniciando por 1 metade são positivos (100, 101, 102, 110 e
111) e metade são negativos (112, 120, 121 e 122).
2-5
Cálculo do valor do número
Um número em complemento de (B–1) tem o seu valor calculado de acordo com os
seguintes passos:
• determinação do sinal: se a representação do número, interpretado como inteiro
positivo, estiver na metade superior da faixa, ele é negativo. Se estiver na metade
inferior da faixa, é positivo. Ou seja, sendo o número a=Σ n-1xiBi, se a≥ B n/2, então
este número em complemento de (B–1) é negativo. Se a<Bn/2, então, em complemento
de (B–1), ele é positivo. Obs.: para bases pares, basta analisar o dígito mais
significativo, conforme já explicado.
Assim, por exemplo, para base 3 com três dígitos, tem-se 33 = 27 representações. A
metade é 13,5, e assim os números de 0 a treze (representados respectivamente por
000 a 111) são positivos, e os de 14 a 26 (representados por 112 a 222) são negativos.
Note-se que existem 14 números positivos, e 13 números negativos.
Em outro exemplo, para base 4 com três dígitos, tem-se 43 = 64 combinações. A
metade é 32, e então os números de 0 a 31 (representados por 000 a 133) são
positivos, e os de 32 a 63 (representados por 200 a 333) são negativos. Existem neste
caso 32 números positivos e 32 números negativos.
• determinação da magnitude do número. Se o número a for positivo, então sua
magnitude é dada por M(a)=Σ n-1xiBi. Se o número a for negativo, para calcular sua
magnitude (valor absoluto) deve-se calcular o complemento de (B–1) de cada
algarismo, ou seja, substitui-se cada dígito pelo seu complemento. Alternativamente,
também é possível manipular todo o número:
M(a)=Σ n-1(B-1-xi)Bi = Σ n-1(B-1)Bi – Σ n-1xiBi = Bn–1–Σ n-1xiBi =Bn–1–a
Assim, por exemplo, para base 3 com três dígitos, a magnitude de 110 é 12 (o número
é positivo). Já o número 112 é negativo, e assim seus dígitos devem ser
complementados, resultando em 110, ou seja, a magnitude também é 12. Utilizando-se
a fórmula acima, tem-se também 33–1–(112)3 = 27–1–14=26–14=12.
A tabela a seguir fornece diversos exemplos do cálculo do valor de um número, de acordo
com as regras descritas acima.
Base
2
2
2
2
3
3
3
10
10
10
10
10
10
Num.dig.
4
4
4
4
3
3
3
2
2
3
3
3
3
Número
1110
1001
1010
0101
102
111
121
98
99
45
54
76
50
Sinal
–
–
–
+
+
+
–
–
–
+
–
-
Magnitude
1
6
5
5
11
13
10
1
0
45
45
23
49
Num.decim.
–1
–6
–5
+5
+11
+13
–10
–1
–0
+45
–45
-23
-49
Tabela 2.7 - Exemplos de cálculo do valor de um número em complemento de B-1
2-6
Troca de sinal
Para trocar o sinal de um número a em complemento de (B–1), basta complementar, também
em B–1, cada um de seus dígitos. Assim, no caso de c=–(a), tem-se, pelo raciocínio acima,
c=Bn–1–a. Note-se que –(–(a)) = –(Bn–1–a) = Bn–1–(Bn–1–a) = a.
No caso de bases ímpares, o maior positivo, ao ser trocado de sinal, resulta novamente em si
próprio. Nestes casos, diz-se que houve estouro de representação (veja seção 2.6). Para
bases pares, isto nunca ocorre (para complemento de B-1). A tabela abaixo ilustra diversos
casos de troca de sinal.
Base
2
2
2
2
3
3
3
10
10
10
10
16
16
16
Num.dig.
4
4
4
4
3
3
3
2
2
2
2
2
2
2
Número
1110
1001
1010
0101
102
111
121
98
99
45
54
01
FF
98
Núm.negado
0001
0110
0101
1010
120
111 (estouro)
101
01
00
54
45
FE
00
67
Magnitude
1
6
5
5
11
13
10
1
0
45
45
1
0
103
Tabela 2.8 - Exemplos de troca de sinal para números em complemento de B-1
Soma de dois números
Para entender-se o processo de soma de dois números em complemento de (B–1), deve-se
analisar os mesmos casos da soma em sinal magnitude. Na Tabela 2.9 a seguir, deseja-se
realizar a soma d=a+c. Os números a e c estão em complemento de (B–1), e quer-se obter d
também em complemento de (B–1). Note-se que um número x, quando for negativo, está
representado por Bn-1-M(x). As quatro primeiras colunas da esquerda da tabela mostram os
mesmos seis casos da soma em sinal/magnitude, e a coluna da direita ilustra o resultado
obtido pela simples soma dos dois operandos, sem analisar-se seus sinais, suas magnitudes
ou se eles devem na realidade ser somados ou subtraídos (ou seja, simplesmente realiza-se a
soma a+c).
Em todos os casos mostrados na Tabela 2.9, usam-se sempre as mesmas tabelas de soma de
números inteiros (não se utilizam tabelas especiais para soma ou subtração em complemento
de (B–1)). Note-se que em três casos, marcados com (*), não se obtém diretamente o
número já representado em complemento de (B–1); existe um termo excedente de Bn–1. Nos
outros três casos, não marcados, o resultado obtido já está correto.
Para reconhecer facilmente os casos que necessitam de correção, basta observar-se que o
termo Bn corresponde a um dígito na posição (n+1). Como os números representados tem
somente n posições, a posição (n+1) só será ocupada naquelas somas que produzirem um
“vai-um”. Assim, se o termo Bn estiver presente, ele só pode ter sido gerado, na soma, por
um “vai-um”. Ou seja, somente os casos que produzirem um “vai-um” são os que
necessitam de correção. Para eliminar o termo Bn, basta eliminar-se este “vai-um”. E para
eliminar o termo (–1), adiciona-se um ao resultado.
2-7
S(a)
S(c)
S(d)
M(d)
+
–
+
–
+
–
M(a)+M(c)
M(a)+M(c)
+
–
se M(a)≥M(c), + M(a)–M(c)
se M(a)<M(c), – M(c)–M(a)
–
+
se M(a)>M(c), – M(a)–M(c)
se M(a)≤M(c), + M(c)–M(a)
Resultado obtido pela
simples soma de a+c
a+c
Bn-1-M(a) + Bn-1-M(c)
Bn-1+Bn-1-(M(a)+M(c))
Bn-1 + Bn-1 - M(d)
Bn-1 + d (*)
M(a) + Bn-1-M(c)
Bn-1 + M(a)-M(c)
Bn-1 + d (*)
M(a) + Bn-1-M(c)
Bn-1 - (M(c)-M(a))
Bn - 1 - M(d)
d
Bn-1 - M(a) + M(c)
Bn-1 - (M(a)-M(c))
Bn-1 - M(d)
d
Bn-1 - M(a) + M(c)
Bn-1 + (M(c)-M(a))
Bn-1 + d (*)
Tabela 2.9 - Soma em complemento de B-1
Simplificando, tem-se a seguinte regra de correção: para obter a soma correta em
complemento de (B–1), basta somar o “vai-um” ao resultado (e eliminar o “vai-um”). Ou,
dito de outra maneira, se ocorrer um “vai-um”, deve-se somar um ao resultado para corrigilo. Se não ocorrer “vai-um”, o resultado já está correto. A tabela a seguir ilustra exemplos de
diversas somas, tanto em base 2 (complemento de um) como em base 10 (complemento de
nove).
Base
2
2
2
2
2
2
2
2
10
10
10
10
10
10
Num.dig.
4
4
4
4
4
4
4
4
2
2
2
2
2
2
a
1110
1111
1001
0110
0101
0011
1111
0001
98
99
99
45
45
76
c
0001
0001
0111
1111
1000
0011
1111
1110
37
00
01
55
45
45
d=a+c
1111
10000
10000
10101
1101
0110
11110
1111
135
99
100
100
90
121
Tabela 2.10 - Exemplos de soma em complemento de B-1
2-8
d corrigido
1111
0001
0001
0110
1101
0110
1111
1111
36
99
01
01
90
22
2 . 3 . 4 Números com sinal: representação em complemento de B
Para representar números em complemento de B, utiliza-se a fórmula Bn–a. Note-se que, ao
contrário de complemento de (B–1), esta fórmula é aplicada sobre todo o número, e não
sobre os seus algarismos individuais. Desta maneira elimina-se a dupla representação do
zero, e faixa de representação fica:
Faixa de representação, para B par:
[ –(Bn/2) , +(B n/2–1) ]
Faixa de representação, para B ímpar:
[ –(Bn–1)/2 , +(B n–1)/2 ]
Note-se que a gama de representação é dividida em dois subconjuntos, um para números
negativos e outro para positivos. Não existe mais a dupla representação do zero. Observe-se
também que as faixas (considerando-se a representação dos números) continuam as mesmas
da representação em complemento de B–1. Como estes números são agora interpretados em
complemento de B, entretanto, os valores das faixas mudam. A faixa positiva permanece a
mesma, mas a faixa negativa sofre um deslocamento de uma unidade, de forma a eliminar o
zero negativo. A tabela a seguir ilustra as faixas para diversas bases.
Base Num.dig.
Faixa
Faixa em decimal
2
4
1000,1001,..,1111,0000,..,0111
–8,–7,..,–1,0,1,..7
3
3
112,120,121,..,222,000,001,..,111 –13,–12,–11,..,–1,0,1,..,13
4
3
200,201,..,333,000,001,..,132,133
–32,–31,..,–1,0,1,..31
8
3
400,401,..,777,000,001,..,376,377
–256,–255,..,–1,0,1,..,255
9
2
45,46,..,88,00,01,..,43,44
–40,–39,..,–1,0,1,..,39,40
10
2
50,51,..,98,99,00,01,..,48,49
–50,–49,..,–2,–1,0,1,..,48,49
Tabela 2.11 - Exemplos de faixas de representação em complemento de B
Na Tabela 2.11, por exemplo, para base decimal com dois dígitos, com números positivos
tem-se a faixa de 0 até 99; com a representação em complemento de 9 obtém-se a faixa de 50
a 99 e 0 a 49. Esta faixa continua a mesma para complemento de 10; e da mesma maneira a
primeira metade (de 50 a 99) representa números negativos; a segunda metade (de 0 a 49)
representa números positivos. Entretanto, agora 99 representa –1 (e não mais zero, como em
complemento de 9) e 50 representa o número –50 (que não tem representação positiva
equivalente!). Ou seja, todos os números negativos sofreram um acréscimo de –1. As
demais propriedades se mantém: um número iniciando por 9, 8, 7, 6 ou 5 é negativo;
iniciando por 0, 1, 2, 3 ou 4 é positivo. Em binário, para 4 dígitos, tem-se a faixa 1000 a
1111 (–8 a –1) e 0000 a 0111 (0 a 7). Números iniciando por 1 são negativos, e iniciando
por 0 são positivos.
Note-se também que agora as bases ímpares tem faixas simétricas, mas que as bases pares
possuem um número negativo a mais, que não tem equivalente positivo dentro da faixa.
Cálculo do valor do número
Um número em complemento de B, tem o seu valor calculado de acordo com os seguintes
passos:
• determinação do sinal: a regra é a mesma de complemento de (B–1): se a
representação do número, interpretado como inteiro positivo, estiver na metade
superior da faixa, ele é negativo. Se estiver na metade inferior da faixa, é positivo. Ou
seja, sendo o número a=Σ n-1xiBi, se a≥ Bn/2, então este número em complemento de
B é negativo. Se a<Bn/2, então sua interpretação é de um número positivo. Obs.: para
bases pares, a regra pode ser simplificada: basta analisar o dígito mais significativo,
conforme já foi explicado.
2-9
• determinação da magnitude do número. Se o número a for positivo, então sua
magnitude é dada por M(a)=Σ n-1xiBi. Se o número a for negativo, para obter seu valor
deve-se calcular o complemento de B do número:
M(a)=Bn–a = Bn – Σ n-1xiBi
Note-se que Bn-1-a é a representação em complemento de (B–1). Assim, uma maneira rápida
de calcular o complemento de B é realizando o complemento de (B–1) de cada algarismo e a
seguir somar um no número resultante. Ou seja, (Bn–1–a)+1 = Bn–a, que é o número
desejado em complemento de B. A tabela a seguir fornece diversos exemplos.
Base
2
2
2
2
2
2
3
3
3
3
10
10
10
10
10
Num.dig.
4
4
4
4
4
4
3
3
3
3
2
2
3
3
3
Número
1110
1001
1010
1000
0101
0111
102
111
112
121
98
99
45
54
50
Sinal
–
–
–
–
+
+
+
+
–
–
–
–
+
–
–
Magnitude
2
7
6
8
5
7
11
13
13
11
2
1
45
46
50
Num.decim.
–2
–7
–6
–8
+5
+7
+11
+13
–13
–11
–2
–1
+45
–46
–50
Tabela 2.12 - Exemplos de cálculo do valor de um número em complemento de B
Troca de sinal
Para trocar o sinal de um número a em complemento de B, basta calcular Bn-a. Ou, pelo
raciocínio acima, calcula-se o complemento de (B–1), complementando cada algarismo, e
depois soma-se um. A tabela a seguir ilustra diversos casos de troca de sinal. Note-se que,
para bases pares, a troca de sinal do menor número negativo (de maior magnitude) provoca
estouro de representação, pois este número não tem equivalente positivo. Em bases ímpares
isto não ocorre.
Base
2
2
2
2
2
3
3
3
10
10
10
10
10
Num.dig.
4
4
4
4
4
3
3
3
2
2
3
3
3
Número
1110
1001
1010
0101
1000
102
111
121
98
99
45
54
50
Núm.negado Magnitude
0010
2
0111
7
0110
6
1011
5
1000 (estouro)
8 (–8)
121
11
112
13
102
10
02
2
01
1
55
45
46
46
50 (estouro)
50 (–50)
Tabela 2.13 - Exemplos de troca de sinal para números em complemento de B
2-10
Soma de dois números
O raciocínio é análogo ao utilizado em complemento de (B–1). Deve-se analisar os mesmos
casos da soma em complemento de (B–1) e da soma em sinal magnitude. Na tabela a seguir,
deseja-se calcular d=a+c. Os números a e c estão representados em complemento de B, e
quer-se obter d também em complemento de B.
A tabela é praticamente uma cópia da usada para complemento de (B–1); comparando-se as
duas nota-se que a diferença está na eliminação de todos os termos “–1” (que é justamente a
diferença entre (B–1) e (B). Como no caso de complemento de B-1, tem-se seis casos a
serem analisados. A coluna da direita mostra o resultado obtido se for realizada simplesmente
uma soma dos dois operandos, sem a preocupação de analisar previamente os operandos.
Em todos os casos, usam-se sempre as mesmas tabelas de soma de números inteiros (não se
utilizam tabelas especiais para complemento de B). Note-se que em três casos, marcados
com (*), não se obtém diretamente o número já representado em complemento de B; existe
um termo excedente de Bn. Nos outros três casos, não marcados, o resultado obtido já está
correto.
S(a)
+
–
S(c)
+
–
S(d)
+
–
M(d)
M(a)+M(c)
M(a)+M(c)
+
–
se M(a)≥M(c), + M(a)–M(c)
se M(a)<M(c), – M(c)–M(a)
–
+
se M(a)>M(c), – M(a)–M(c)
se M(a)≤M(c), + M(c)–M(a)
d (Soma de a + c)
a+c
Bn-M(a) + Bn-M(c)
Bn+Bn - (M(a)+M(c))
Bn + Bn - M(d)
Bn + d (*)
M(a) + Bn-M(c)
Bn + M(a)-M(c)
Bn + d (*)
M(a) + Bn-M(c)
Bn - (M(c)-M(a))
Bn - M(d)
d
Bn - M(a) + M(c)
Bn - (M(a)-M(c))
Bn - M(d)
d
Bn - M(a) + M(c)
Bn + (M(c)-M(a))
Bn + d (*)
Tabela 2.14 - Soma em complemento de B
Os casos a serem corrigidos são identificados da mesma maneira que em complemento de
(B–1). Somente os casos que produzirem um “vai-um” são os que necessitam de correção.
Para eliminar o termo B n, basta eliminar este “vai-um”; não existe a necessidade de somar
um ao resultado. Para todos os fins práticos, esta “eliminação” é realizada simplesmente
ignorando-se a existência do “vai-um” em um primeiro momento (a ocorrência ou não do
“vai-um” ainda pode influenciar a análise do resultado da soma, mas não a soma
propriamente dita).
A tabela a seguir ilustra exemplos de diversas somas, tanto em base 2 como em base 10,
considerando que os números estão representados em complemento de B.
2-11
Base
2
2
2
2
2
2
2
2
10
10
10
10
10
10
Num.dig.
4
4
4
4
4
4
4
4
2
2
2
2
2
2
a
1110
1001
1111
0110
0101
0011
1111
0001
98
99
99
45
45
76
c
0001
0111
0001
1111
1000
0011
1111
1110
37
00
01
55
45
45
d=a+c
1111
10000
10000
10101
1101
0110
11110
1111
135
99
100
100
90
121
d corrigido
1111
0000
0000
0101
1101
0110
1110
1111
35
99
00
00
90
21
Tabela 2.15 - Exemplos de soma em complemento de B
2 . 4 Comparação entre os métodos
Dos quatro métodos estudados nas seções anteriores, dois são amplamente utilizados: o de
representação de números positivos e o de representação em complemento de B. Nestas duas
representações, somas são realizadas através das mesmas tabelas; nenhum procedimento
especial é necessário para somar-se dois números em complemento de dois (exceto a
eventual eliminação do “vai-um”). Os outros dois métodos, de sinal magnitude e de
complemento de (B–1), sofrem da desvantagem de necessitarem de procedimentos mais
complexos para realização da soma, além de apresentarem duas representações para o zero.
Em sistemas atuais, a base é binária e utiliza-se para tratamento de números negativos a
representação em complemento de 2.
A título de comparação, a tabela a seguir mostra a interpretação decimal de números binários
de 4 dígitos nas quatro maneiras analisadas.
Binário
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
Int.positivo
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
sinal mag.
+0
1
2
3
4
5
6
7
–0
–1
–2
–3
–4
–5
–6
–7
compl. de 1
0
1
2
3
4
5
6
7
–7
–6
–5
–4
–3
–2
–1
–0
compl. de 2
0
1
2
3
4
5
6
7
–8
–7
–6
–5
–4
–3
–2
–1
Tabela 2.16 - Interpretação de números binários
2-12
2 . 5 Subtração
A operação de subtração, seja qual for o método de representação utilizado, pode ser
facilmente realizada transformando-a em uma soma:
d = a – c = a + (–c)
Assim, para realizar subtrações, pode-se simplesmente trocar o sinal do subtraendo e somálo ao minuendo. A troca de sinal e a soma seriam então realizadas de acordo com o sistema
de representação utilizado.
A subtração pode, também ser realizada através de tabelas próprias. Neste caso, no lugar de
“vem-um” (carry in), tem-se o “emprestou-um”(borrow in); e no lugar de “vai um” (carry
out) tem-se o “pede-um” (borrow out).
a
0
0
1
1
c
0
1
0
1
d=a-c
0
1 e “pede-um”
1
0
Tabela 2.17 - Tabela verdade de um meio-subtrator
a
0
0
0
0
1
1
1
1
c
0
0
1
1
0
0
1
1
emprestou um
0
1
0
1
0
1
0
1
d=a–c
0
1
1
0
1
0
0
1
pede um
0
1
1
1
0
0
0
1
Tabela 2.18 - Tabela verdade de um subtrator completo
Apesar destas tabelas serem análogas às utilizadas para a soma, a grande maioria dos
computadores não as utiliza; subtrações são realizadas internamente usando-se o método do
complemento do subtraendo.
2 . 6 Estouro de representação
Os números representados em um computador são limitados. Quanto maior o número de
dígitos disponíveis, maior será a faixa dos números representáveis, mas esta faixa sempre
será finita. Assim, ao realizar-se a soma (ou subtração) de dois números, o resultado pode
cair fora da faixa representável. Nestes casos, diz-se que houve estouro ou transbordamento
da representação (overflow). Para representar corretamente o resultado quando ocorreu
estouro necessitaria-se de um dígito a mais para representar o número.
Por exemplo, para números binários de 4 dígitos, tem-se:
1000 + 0001 = 1001
1000 + 1111 = 0111
0111 + 1111 = 0110
0111 + 0011 = 1010
–8 + 1 = –7
–8 + –1 = 7
7 + –1 = 6
7 + 3 = –6
(correto)
(incorreto; deveria ser –9)
(correto)
(incorreto; deveria ser 10)
Note-se que o estouro não está diretamente relacionado com o “vai-um”. Os exemplos acima
ilustram isto. No primeiro caso, não ocorreu nem estouro nem “vai-um”; no segundo caso
2-13
ocorreram tanto estouro como “vai-um”; no terceiro caso ocorreu “vai-um”, mas não estouro;
e no quarto caso não ocorreu “vai-um”, mas ocorreu estouro.
Existe uma regra simples para determinação de estouro em complemento de 2: ocorre estouro
quando o “vai-um” do dígito mais significativo é diferente do “vem-um” para este mesmo
dígito. Note-se que o dígito mais significativo é o utilizado para indicar o sinal do número.
Esta é a maneira como os computadores internamente calculam se o resultado “estourou” ou
não.
Uma outra maneira, que não necessita da análise dos “vai-um” e “vem-um”, utiliza somente
os dígitos mais significativos dos dois operandos e do resultado, ou seja, analisam-se os
sinais dos operandos e do resultado. Esta análise está resumida na tabela a seguir (seja
d=a+c).
Sinal de a Sinal de c
+
+
+
+
–
–
–
–
+
–
–
+
Sinal obtido para d
+
–
–
+
+/–
–/+
Sinal real de d
+
+
–
–
+/–
–/+
Estouro
Não
Sim
Não
Sim
Nunca ocorre
Nunca ocorre
Tabela 2.19 - Análise dos casos de estouro de representação
Pela tabela, pode-se observar que:
• se os dois operandos tiverem sinais diferentes, nunca ocorre estouro (a representação
do resultado sempre estará dentro da faixa).
• somente ocorre estouro quando os dois operandos tiverem sinais iguais, e este sinal é
diferente do sinal obtido para o resultado. Ou seja, quando somando-se dois números
positivos obtém-se um resultado negativo, e quando somando-se dois números
negativos obtém-se um número positivo. Nestas duas situações, o sinal do resultado
está obviamente incorreto, e esta é uma indicação clara que ocorreu estouro de
representação.
Assim, em uma soma, ocorre estouro quando S(a)=S(c) e S(a)≠S(d). Analogamente, em
uma subtração ocorre estouro quando S(a)≠S(c) e S(a)≠S(d).
2 . 7 Exercícios propostos
1. Qual o valor decimal de 011011012? Qual a representação binária de 654?
2. Converter para binário os seguintes números decimais:
(a) 39
(b) 0,4475
(c) 256,75
(d) 129,5625
3. Converter para decimal os seguintes números binários:
(a) 01101
(b) 0,001101
(c) 0111011,1011
(d) 010110011
4. Quantos números diferentes podem ser representados em uma palavra binária de 6 bits?
5. Quantos números diferentes podem ser representados em um conjunto de 4 chaves, cada
uma com três posições diferentes?
6. Escrever os 12 primeiros números no sistema de numeração de base 5.
2-14
7. Escrever os 26 primeiros números no sistema de numeração de base 12. Usar a letra A
para o decimal 10 e a letra B para o decimal 11.
8. Representar o número 12,1 em binário de dez bits, com 5 bits de parte inteira e 5 bits de
parte fracionária.
9. Represente o número –4710 usando representações binárias de 8 bits em (a) sinal e
magnitude, (b) complemento de um e (c) complemento de dois.
10. Converter os seguintes números hexadecimais em decimais:
(a) B6C7
(b) D2763
(c) 9,1A
11. Converter os seguintes números octais em binário:
(a) 56
(b) 32,234
(c) 231,2
(d) 3364
12. Converter os seguintes números hexadecimais em binários:
(a) AB2
(b) 12,A
(c) 649
(d) 0,D19
13. Converter os seguintes números binários em hexadecimais:
(a) 010110111
(b) 011110,01011
(c) 01110100010101
14. Considerando um processador que opere com a base quaternária utilizando 5 bits.
14.1 Para números inteiros positivos:
a) Quantos números diferentes podem ser representados? (Fórmula de cálculo e valor
decimal)
b) Quais são os limites inferior e superior desta faixa? (Valor quaternário e decimal
correspondente)
c) Como seria representado o número 126 neste sistema?
14. 2 Supondo que se queira representar os números inteiros com sinal, usando sinal e
magnitude:
a) Quantos números diferentes podem ser representados? (Fórmula de cálculo e valor
decimal)
b) Quais são os limites inferior e superior desta faixa? (Valor quaternário e decimal
correspondente)
c) Como seria representado o número 126 neste sistema?
d) Como seria representado o número -126 neste sistema?
14.3 Agora supondo que se quer representar estes números usando complemento de B-1:
a) Quantos números diferentes podem ser representados? (Fórmula de cálculo e valor
decimal)
b) Quais são os limites inferior e superior desta faixa? (Valor quaternário e decimal
correspondente)
c) Como seria representado o número 126 neste sistema?
d) Como seria representado o número -126 neste sistema?
14.4 Agora supondo que se quer representar estes números usando complemento de B:
a) Quantos números diferentes podem ser representados? (Fórmula de cálculo e valor
decimal)
b) Quais são os limites inferior e superior desta faixa? (Valor quaternário e decimal
correspondente)
c) Como seria representado o número 126 neste sistema?
d) Como seria representado o número -126 neste sistema?
15. Considere os pares de números binários de 6 bits indicados abaixo. Efetue a operação de
soma entre eles supondo, independentemente, que:
1) os números estão representados em sinal e magnitude;
2) os números estão representados em complemento de um;
2-15
3) os números estão representados em complemento de dois.
Para cada caso, interprete o resultado, isto é, determine qual é o seu valor numérico e indique
se este valor é o resultado correto da operação para a forma de representação sugerida.
(a) 010101 e 110110
(b) 010101 e 010110
(c) 110101 e 110110
16. Efetuar as seguintes subtrações em um sistema decimal de 4 dígitos, utilizando uma vez
complemento de 9 e outra vez complemento de 10:
(a) 1024–913
(b) 249–137
(c) 119–239
17. Repetir o exercício 16, agora para um sistema binário de 12 bits, uma vez utilizando
complemento de um e outra vez com complemento de dois.
18. Efetuar as operações indicadas abaixo (em decimal) em um sistema binário de 10 bits,
com notação em complemento de dois. Analise o resultado, indicando a eventual existência
de estouro de representação:
(a) 475 + 128
(b) - 506 + -6
(c) 436 – 475
(d) 506 + 6
(e) 128 – 128
(f) - 475 + 511
19. Converta os números 17 e 15 para binário usando 6 bits e efetue a operação de soma
entre eles (17+15), usando as seguintes representações:
a) sinal magnitude;
b) complemento de um;
c) complemento de dois.
Analise os resultados obtidos quanto à correção (sem calcular o seu valor correspondente em
decimal).
20. Repita o exercício 19 para os números 13 e 8.
21. Repita o exercício 19 para os números -17 e -15 (realizando a soma -17+(-15)).
22. Mostre como somar em complemento de um, para n=6 bits, as seguintes parcelas
decimais:
(a) 27 e –7
(b) 27 e 8
(c) 1 e 5
23. Repetir o exercício 23, com as parcelas codificadas em complemento de dois, também
para 6 bits.
24. Usando a técnica de subtrair através de complemento do subtraendo, mostrar como obter
as seguintes diferenças em binário, 6 bits, complemento de um:
(a) 8 – 7
(b) -16 – 16
(c) 15 – 24
25. Repetir o exercício 25 para complemento de dois em 6 bits.
26. Repetir o exercício 25 para sinal / magnitude.
27. Converta os seguintes números para binário, usando a representação destinada a inteiros
positivos, usando o número necessário de bits e efetue a subtrações indicadas usando a
tabela de subtração:
(a) 32 - 15
(b) 31 - 14
(c) 17 - 9
28. Supondo um sistema decimal, com 4 dígitos, que trabalhe com representação de
negativos em complemento de 9, mostre como realizar as operações:
(a) 0136 + 7654
(b) 9998 + 7777
(c) 0010 – 0108
29. Repetir o exercício 28 para representação em complemento de 10.
2-16