1. A figura 1a representa um transistor NMOS de reforço a funcionar

1º Teste de Electrónica I
2º Semestre 2010/2011
06 de Maio de 2011
Duração: 1h30m
1a
2,0
Cotação
Classificação
1b
1,5
Curso________________________
Número ________
Nome
1c
1,5
1d
2,0
2a
1,0
2b
2,0
2c
2,0
_
2d
2,0
3a
2,5
3b
2,5
3c
1,0
Final
20
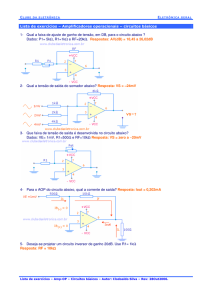
1. A figura 1a representa um transistor NMOS de reforço a funcionar numa montagem de fonte-comum. A tensão
de entrada vI varia entre 0 e 2 volt.
a) Determine o valor da resistência de dreno RD de modo a que quando vI = 2V o transistor esteja no limiar tríodo /
saturação. Sol: VGD = Vt = vI - (VDD – K (vI - Vt)2 (1 + λ (vI - Vt)) RD ⇒ RD = 258Ω
b) Supondo que aplica à entrada uma tensão vI a variar com uma forma triangular como se representa na figura 1b,
esboce o andamento da tensão de saída v0, nas condições da alínea anterior. Sol: azul-escuro na figura
VDD
VDD
VDD = 5 V
K = 10 mA / V2
RD
Vt = 0,8 V
T
vI
vO(vI=2V)=1,2V
λ = 0,02 V-1
vO
Vt
1b
Figura 1
1a
c) Para polarizar o transistor a meio em corrente entre a saturação e o corte calcule o valor das duas resistências RG1
e RG2 de um divisor de tensão a colocar na porta. O paralelo destas resistências RG1//RG2 deve ser igual a 100kΩ.
Sol: IDQ = 7,37 mA ⇒ vI = 1,633 V ⇒ RG1 = 306 kΩ e RG2 = 148,5 kΩ.
d) Se excitar o circuito que obteve na alíea anterior com um gerador de sinal fraco com uma resistência interna de
1kΩ determine o ganho de tensão incremental Gv = vo / vi. Sol: gm = 8,59 mS, ro = 7,2 kΩ, Gv = -2,12.
+VCC
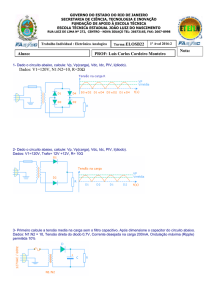
2. Considere o circuito representado na figura 2, em que VCC=3V,
RC=1kΩ, RE=1kΩ, RB1=130kΩ, RB2=50kΩ. O transistor é
caracterizado por: VCEsat = 0,2V, β=150 e VBEon=0,6V.
RC
RB3
iC2
vOUT
TJB2
vin
a) Explique a função de TJB1 e TJB2 no circuito amplificador. Sol:
TJB1 fonte de corrente DC de polarização de TJB2 que é amplificador em
emissor comum.
b) Calcule o valor da corrente de repouso IC2. Sol: IC2 ≈ IC1 = 1,1 mA.
RB1
TJB1
RB2
-VCC
RE
CE
Fig 2
c) Dimensione a resistência RB3 para que se tenha em repouso vOUT =
0. Verifique que os TJBs ficam na zona activa. Sol: impossível
porque vOUT = VCC – RC IC1 e IC1 independente de RB3.
d) Sabendo que o gerador a colocar na entrada tem uma impedância
de 1kΩ, obtenha uma estimativa do valor do polo introduzido pelo
condensador CE = 1 µF. Despreze o efeito dos demais condensadores
do circuito. Jusrtifique esta aproximação.
Sol: fP = 5,3 kHz (Req CE é praticamente só a impedância vista para o emissor do TJB2 porque é muito mais pequena que
todas as outras ((rπ + Rg) / β) e o pólo é então o maior (dominante) logo os outros condensadores já são equivalentes a um
CC.
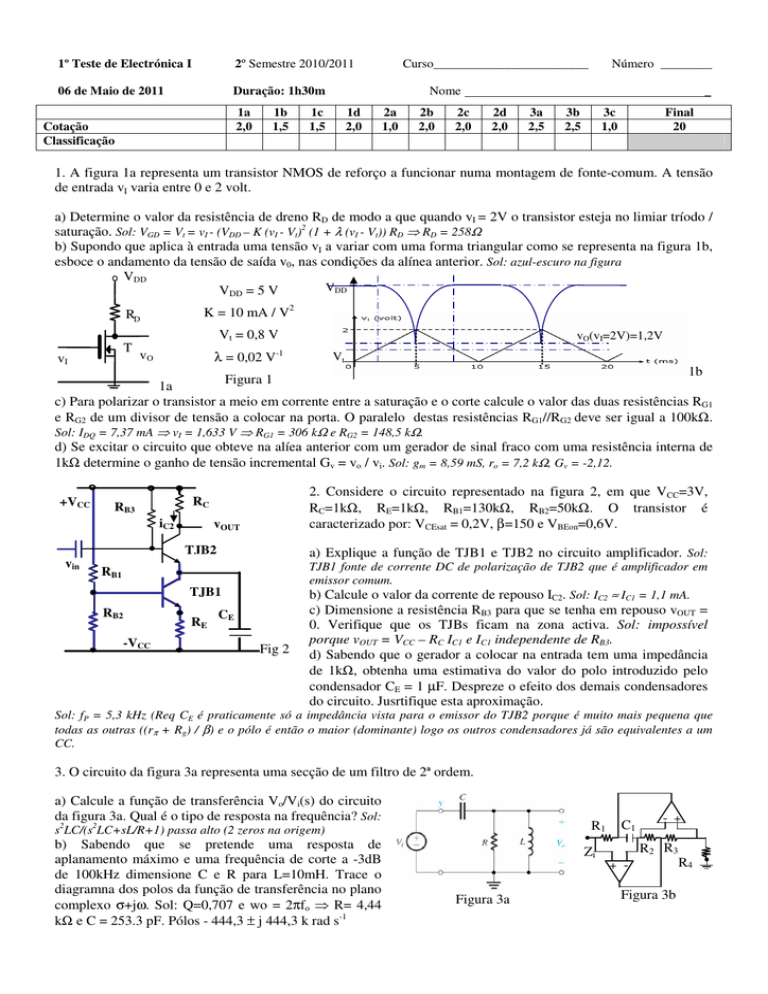
3. O circuito da figura 3a representa uma secção de um filtro de 2ª ordem.
a) Calcule a função de transferência Vo/Vi(s) do circuito
da figura 3a. Qual é o tipo de resposta na frequência? Sol:
R1
s2LC/(s2LC+sL/R+1) passa alto (2 zeros na origem)
b) Sabendo que se pretende uma resposta de
aplanamento máximo e uma frequência de corte a -3dB
de 100kHz dimensione C e R para L=10mH. Trace o
diagramna dos polos da função de transferência no plano
complexo σ+jω. Sol: Q=0,707 e wo = 2πfo ⇒ R= 4,44
kΩ e C = 253.3 pF. Pólos - 444,3 ± j 444,3 k rad s-1
C1
- +
R2 R3
Zi
+ -
Figura 3a
Figura 3b
R4
c) Supondo que na figura 3b todas as resistências são de 10kΩ dimensione o condensador C1 por forma a simular a
bobina do filtro da figura 3a. Qual é o interesse prático deste circuito? Sol: Zi = R1 R2 R4 C1 s / R3 ⇒ C1 = 100 pF.
JCF
Formulário sobre os transístores MOS:
[
i D = k n 2( v GS - VTn ) v DS - v 2DS
]
iD = iDS = kp (vSG-|VTp|)2 (1+λvSD)
[
2
i D = k p 2( v SG - VTp ) v SD - v SD
k n ,p =
1
W
µ C
2 n ,p ox L
]
[AV -2 ]
iD = iDS = kn (vGS-VTn)2 (1+λvDS)
kn,p = k’n,p (W/L)
Formulário sobre os transístores bipolares:
iB = (IS/β) (exp(vBE/nVT)-1)
iC = β iB
Aproximações:
n2
AButt(Ω) = 10 log (1 + |ε Ω | )
ACheb(Ω>>1)≅ 20 log (ε 2
Filter Order Chebyshev
n-1 n
Ω )
com
Ω = ω / ωp
Butterworth sP=1
1
1.00s + 1
s+1
2
1.41s2 + 0.911s + 1
s2 + 1.41s + 1
3
3.98s3 + 2.38s2 + 3.70s + 1
s3 + 2.00s2 + 2.00s + 1
4
5.65s4 + 3.29s3 + 6.60s2 + 2.29s + 1
s4 + 2.61s3 + 3.41s2 + 2.61s + 1
5
15.9s5 + 9.11s4 + 22.5s3 + 8.71s2 + 6.48s + 1
s5 + 3.24s4 + 5.24s3 + 5.24s2 + 3.24s + 1