Controle Neural Aplicado a um Conversor Boost Utilizado

Anais do XX Congresso Brasileiro de Automática
Belo Horizonte, MG, 20 a 24 de Setembro de 2014
CONTROLE NEURAL APLICADO A UM CONVERSOR BOOST UTILIZADO EM
AEROGERADORES DE BAIXA POTÊNCIA
THIAGO TONON*, HÉLIO VOLTOLINI†, ALESSANDRO GOEDTEL*
*Universidade Tecnológica Federal do Paraná (UTFPR) – Campus Cornélio Procópio
Av. Alberto Carazzai, 1640 – Cornélio Procópio, Paraná, Brasil
†Universidade Tecnológica Federal do Paraná (UTFPR) – Campus Ponta Grossa
Av. Monteiro Lobato, s/n – Ponta Grossa, Paraná, Brasil
E-mails: [email protected], [email protected],
[email protected]
Abstract
 This paper presents the study, design and simulation of a DC-DC boost converter with output voltage control techniques using neural networks. The boost converter studied in this work is being used in a low power wind turbine. Due to operation at variable speed wind turbine, the input voltage to the converter is also variable, and the output should be stabilized to a
fixed voltage. This means that there is a need to control the converter so that the differences in input voltages are compensated.
Thus, a PI controller was designed using the method of root locus. The modeling of the boost converter is also presented. The
controller operates in the time of performance of key power used in the converter, thereby controlling the output voltage. The
variation in input voltage causes the driver does not act correctly for every operating point. Therefore, an adaptive controller becomes necessary. One Neural Controller was designed in this way to make it work as adaptive controller, compensating for the
difference in the converter input voltage. The validation of controls was performed by simulation using MATLAB/Simulink
software , to validate the theoretical development presented in the work.
Keywords
 Modeling Boost Converter , Simulation Boost Converter, PI Control, Neural Control, Low Power Wind Generator.
Resumo
 Este artigo apresenta o estudo, projeto e simulação de um conversor CC-CC tipo boost, com controle de tensão de saída utilizando técnicas de redes neurais. O conversor boost estudado neste trabalho está sendo utilizado em um aerogerador de
baixa potência. Devido à operação em velocidade variável do aerogerador, a tensão de entrada no conversor também é variável, e
a saída deve ser estabilizada para uma tensão fixa. Isso faz com que haja a necessidade do controle do conversor para que as diferenças de tensões de entrada sejam compensadas. Assim, foi projetado um controlador PI utilizando o método de lugar das raízes.
A modelagem do conversor boost também é apresentada. O controlador atua no tempo de atuação da chave de potência utilizada
no conversor, controlando assim a tensão de saída. A variação na tensão de entrada faz com que o controlador não atue de forma
correta para todo ponto de operação. Por isso, um controlador adaptativo faz-se necessário. Um Controlador Neural foi projetado,
dessa forma, para que trabalhe como controlador adaptativo, compensando a diferença de tensão de entrada do conversor. A validação dos controles foi efetuada através de simulação utilizando o software Matlab/Simulink, para validação do desenvolvimento
teórico apresentado no trabalho.
Palavras-chave
 Modelagem Conversor Boost, Simulação Conversor Boost, Controle PI, Controle Neural, Aerogerador de
Baixa Potência.
1
Técnicas convencionais de controle desses conversores consideram os componentes como ideais,
sem perdas, e com funcionamento linear. Assim, o
ponto de operação do sistema é estável, podendo ser
modelado como um sistema de equações lineares. A
partir dessas equações, um projeto de controle pode
ser desenvolvido.
Entretanto, na prática, esses componentes não
apresentam condições de funcionamento lineares,
tornando o sistema altamente não linear. Além disso,
a tensão de entrada, assim como a carga, pode variar,
tornando o sistema instável. Por isso, uma solução é
a utilização de sistemas de controles adaptativos.
(MAHDAVI, 2005).
Umas das opções de controles adaptativos é a
utilização de controles neurais. Algumas soluções de
implementação de redes neurais podem ser encontradas, como em (JAWHAR, 2006) e (KABOLI, 2013)
que propõem o ajuste dos ganhos do PI utilizando
sistemas neuro-fuzzy. Em (HASSAN, 2010) é pro-
Introdução
Os geradores eólicos possuem como característica principal de funcionamento o torque mecânico
aplicado ao gerador proporcional ao vento. Assim, há
a necessidade de padronizar a tensão de saída desse
gerador para o aproveitamento dessa potência gerada.
Em geral, para geradores de baixa potência, o
gerador utilizado no projeto gera tensões com amplitude e frequência que dependem da velocidade do
vento. Na sequência, um sistema eletrônico converte
a tensão de amplitude e frequência variável em tensão contínua e, na sequência, a tensão contínua em
tensão alternada com amplitude e frequência fixas.
Assim, a utilização de conversores é a solução
para o fornecimento de tensão de amplitude fixa na
saída do gerador. Diversas topologias de conversores
podem ser encontradas. Nesse artigo, o conversor
utilizado é o conversor elevador de tensão tipo boost.
3743
Anais do XX Congresso Brasileiro de Automática
Belo Horizonte, MG, 20 a 24 de Setembro de 2014
lar a tensão de saída do conversor pela razão cíclica da chave de potência.
O conversor foi projetado para que possa operar
sempre em modo contínuo. Dessa forma, somente
duas configurações são possíveis para este circuito:
uma quando a chave de potência está fechada e outra
quando a chave está aberta.
Durante cada faixa de operação, os espaços de
estados são compostos pela corrente no indutor e
pela tensão no capacitor. Foi incluído no projeto
também os valores de resistência interna do indutor e
a resistência interna da chave de potência.
Sendo a tensão de entrada do conversor, as
matrizes e representam, respectivamente, as
matrizes para o sistema com a chave de potência
comutada e para a chave não comutada. As matrizes
e representam vetores para o mesmo modo de
funcionamento. Assim:
posto o controle PI neural para controle da posição
de servo atuando em sistemas pneumáticos,
(ROSTAMI, 2010) propõe uma rede neural para
previsão de ações futuras na planta para ação do
controle PI, (UTOMO, 2011) aplica uma rede neural
no controle do erro de um conversor buck-boost,
obtendo a razão cíclica da chave a partir da diferença
entre a tensão de saída e a tensão desejada e da diferença entre a tensão de saída atual com a tensão anterior e (DHIVYA, 2013) propõe um controle neural
para um conversor boost a partir da leitura de quatro
variáveis do sistema para obtenção da razão cíclica
do conversor.
O conversor boost utilizado nesse projeto faz
parte de um aerogerador de baixa potência. O gerador utilizado é um Gerador Síncrono de Imãs Permanentes (GSIM). A partir da entrada de torque na
máquina, gerado a partir da turbina eólica, o gerador
gera uma tensão com amplitude e frequência que
varia conforme a velocidade do vento. A saída desse
gerador é conectada a um conversor CA-CC não
controlado. A saída desse conversor fornece tensão
CC com amplitude variável para o conversor boost
que deverá fornecer uma tensão CC com amplitude
fixa na sua saída, para enfim, ser convertido em tensão CA pelo inversor de frequência. A faixa de operação de tensão de entrada é entre 50V e 350V. A
Figura 1 apresenta o diagrama do sistema que faz
parte desse projeto.
. . durante δ.τ
. . durante (1 - δ).τ
(1)
(2)
Para o conversor boost, duas variáveis de estados são definidas:
(3)
. durante δ.τ
(4)
Onde é a corrente do indutor e é a tensão
no capacitor.
As variáveis de saída podem ser escritas pelas
variáveis de entradas, através de:
. durante (1 - δ).τ
(5)
Visando a descrição média das variáveis em um
determinado período de chaveamento, as equações
correspondentes a cada período de funcionamento
podem ser escritas como:
Figura 1. Diagrama do Gerador Eólico.
. . 1 . . . 1 . Dessa forma, o objetivo é projetar, através de
técnicas de redes neurais, um controle adaptativo
capaz de controlar a tensão de saída do conversor
boost buscando o melhor ponto de operação de acordo com a variação de tensão de entrada. O controlador irá operar em malha fechada regulando a tensão
de saída para um valor fixo independente da variação
da tensão de entrada.
. . 1 . (6)
(7)
Considerando que a tensão de entrada é sem variação, então .
Utilizando as equações anteriores, e considerando que 0, tem-se:
2 Modelagem do conversor Boost
. . . . . . ɗ
2.1 Obtenção /
Para o desenvolvimento do controle do conversor, é necessária a obtenção da função de transferência do conversor. A proposta deste trabalho é contro-
Desprezando as variações de
finição, são pequenas, temos:
. " . 1 "
3744
(8)
e ɗ, que, por de(9)
Anais do XX Congresso Brasileiro de Automática
Belo Horizonte, MG, 20 a 24 de Setembro de 2014
. " . 1 "
# . . $ . . . . ɗ
(14)
v
Figura 2. Conversor boost.
A modelagem matemática desse conversor foi
desenvolvida de acordo com (ERICKSON, 2001).
Este conversor possui dois pontos de operação distintos: um quando a chave de potência está em operação, e outro quando a chave de potência não está em
operação.
2.3 Chave de potência em condução
(15)
Quando a chave de potência do conversor está
em condução, sua topologia pode ser expressa conforme a Figura 3.
Em regime permanente, tem-se:
(16)
i
Vi
. # . (18)
. . . . . ɗ
(19)
. % # . . . ɗ
(20)
L
Rl
+ Vl -
(17)
Através das equações (16) e (12), é possível obter a relação entrada/saída em regime permanente:
Malha 1
ic
Ron
C
Nó 1
Ro
+
v
-
Figura 3. Conversor boost com chave em condução.
Com a chave de potência em condução, a fonte
fornece corrente para o indutor que está conectado
em série com uma resistência interna ' , e com a
resistência interna da chave '() .
A tensão de saída, nesse modo de operação, é a
tensão que está sobre o capacitor. O diodo não conduz nesse modo, pois a tensão na saída do inversor é
maior que a tensão de entrada.
Para esse modo de operação, aplicando a Lei de
Kirchhoff das tensões (LKT) na malha, obtém-se:
Aplicando a transformada de Laplace à equação
(13), tem-se:
ou
' . '() . 0
onde I é a matriz identidade.
Por fim, a função de transferência pode ser expressa por:
$ . . % # . . ɗ
. . Ro
-
Da mesma forma:
& +
ic
C
(12)
(13)
$ . . . ɗ
Ron
(11)
. . . . ɗ
. Vd
Vi
Considerando a componente alternada:
. " . 1 "
Rl
+ Vl -
A equação (8) representa o comportamento em
regime permanente do sistema. Anulando os termos
variáveis no tempo e as perturbações, resulta-se em:
. . 0
L
i
(10)
(22)
Sabendo que a queda de tensão no indutor é descrita como:
*.
(21)
+
(23)
Substituindo (23) em (22) e isolando o termo derivativo, encontra-se:
' '() . + *
*
2.2 Modelagem do Conversor Boost
A topologia do conversor boost é apresentada na
Figura 2.
3745
(24)
Anais do XX Congresso Brasileiro de Automática
Belo Horizonte, MG, 20 a 24 de Setembro de 2014
Substituindo (23) em (30) e isolando o termo derivativo, encontra-se:
Aplicando a Lei de Kirchhoff das correntes
(LKC) no nó 1, obtém-se:
0
'
(25)
+
(26)
+ '. (27)
' . 2
+
* *
*
*
Sabendo que a corrente sobre o capacitor é descrita como:
.
Aplicando a Lei de Kirchhoff das correntes
(LKC) no nó 1, obtém-se:
Substituindo (26) em (25) e isolando o termo derivativo, encontra-se:
3 0
Rl
2 '
, + - , *
1
+
(28)
(29)
- Vl +
Vi
Malha 1
Vd
Ro
1. . /
2 (35)
(36)
A relação de tensão de saída pela razão cíclica
do conversor boost pode ser descrita por:
+
ic
1
* - . ./
1
'. 1
*
, - . 1
*
3 0
Nó A
C
(34)
A expressão na forma matricial é descrita por
(35) e (36)
Quando a chave de potência do conversor está
em corte, ou seja, não está conduzindo, sua topologia
pode ser expressa conforme a Figura 4.
L
(33)
+ '. 2.4 Chave de potência em corte
i
+
Operando nessa topologia, e aplicando a lei de
Kirchhoff das tensões (LKT) na malha 1, obtém-se:
-.. /
1
'. 1. . /
(32)
.
0
1
0* 1 . 0
'
Substituindo (26) em (32) e isolando o termo derivativo, encontra-se:
A expressão na forma matricial desse sistema é
descrita por (28) e (29).
' '()
*
, + - ,
0
+
(31)
" 1
v
-
(37)
O conversor boost utilizado neste trabalho possui as características descritas pela Tabela 1.
Figura 4. Conversor boost com chave em corte.
Tabela 1. Parâmetros do conversor boost.
Nesta topologia, o indutor passa a descarregar
sua energia armazenada. A tensão de saída é a somatória da tensão da fonte mais a tensão que o indutor
está fornecendo. O diodo passa a conduzir, pois a
tensão de saída é menor que a tensão de entrada.
Parte da corrente carrega o capacitor e parte é fornecida na saída.
Operando nessa topologia, e aplicando a lei de
Kirchhoff das tensões (LKT) na malha 1, obtém-se:
' . 2 0
Tensão de entrada (VCC)
Tensão de saída (VCC)
Indutor
Resistência do indutor
Capacitor
Resistência IGBT ('() )
Frequência de chaveamento
(30)
3746
50 a 350V
400V
940mH
307Ω
940μF
1mΩ
30kHz
Anais do XX Congresso Brasileiro de Automática
Belo Horizonte, MG, 20 a 24 de Setembro de 2014
3 Controle do conversor Boost
projeto do controle PI foi gerada sem considerar as
perdas do circuito. Dessa forma, o controle encontrado para este projeto não expressa o melhor controle
possível para este sistema. Entretanto, com a utilização dos dados gerados a partir dessa escolha, a rede
neural foi treinada para validar sua eficiência. Esta
escolha foi feita justamente para mostrar a capacidade de a rede neural trabalhar no controle de sistemas
que não podem ser modelados, ou seu modelo matemático não representa fielmente o modelo físico a ser
controlado.
Então, sem considerar as perdas do indutor e da
chave, e considerando uma tensão de entrada de
300V, a função de transferência obtida foi:
3.1 Redes Neurais Artificiais
Uma Rede Neural Artificial (RNA) é composta
por uma série de elementos simples, denominados
Neurônios Artificiais. Esses neurônios são desenvolvidos baseados na estrutura do neurônio de um ser
vivo, onde sua saída é a somatória das entradas, ponderadas por um peso sináptico. Dessa forma, o conjunto de neurônios trabalhando em paralelo são capazes de fazer com que uma saída da rede neural possa
representar um sistema a partir de suas entradas.
Uma Rede Neural é capaz de aprender o funcionamento de determinado sistema, sem que haja a
necessidade de se modelar o problema proposto. Isso
porque o seu processo de aprendizado consiste em
apresentar à rede um padrão de funcionamento de
determinado sistema. Assim, a rede é capaz de
aprender seu funcionamento baseado nas informações que são dispostas para o aprendizado.
Uma grande vantagem da utilização de uma
RNA é que, a partir do aprendizado para determinados pontos de operação, a rede consegue generalizar
soluções para pontos de operação que não foram
apresentados durante o treinamento. Portanto, para o
aprendizado, é necessário apresentar os padrões de
funcionamento em alguns pontos de operação.
A rede neural tem capacidade de trabalhar como
um aproximador de funções. A saída do controle, no
tempo, pode ser descrita como uma função. Por isso,
a utilização da rede neural como controlador pode ser
empregada, uma vez que a rede fará a aproximação
de seu sinal de saída conforme o sinal de entrada.
Dessa forma, para que a rede tenha os parâmetros de
funcionamento do sistema, um controle convencional
deve ser desenvolvido para que sirva como fonte de
dados para o treinamento da rede neural.
& Figura 5. Lugar das raízes do sistema.
Através da figura, é possível perceber que o zero
do sistema em malha fechada está no semi-plano
direito. O controlador deve compensar os polos e os
zeros do sistema, para que possa se tornar estável.
Utilizando a ferramenta rltool do Matlab, o
compensador foi encontrado. Para que o controlador
seja capaz de compensar o sistema, é necessária a
alocação de um polo próximo à origem, que fará o
papel de integrador, um zero conjugado para compensar os polos conjugados e mais um polo no semiplano esquerdo. O compensador encontrado atendendo esses requisitos é expresso em (40).
O controlador utilizado no projeto é o controlador do tipo Proporcional Integral (PI). Para este trabalho, o projeto utiliza o método do Lugar das Raízes
para sintonia do controlador.
Para o estudo do Lugar das Raízes, é necessário
conhecer a função de transferência do sistema.
Aplicado os dados da Tabela 1 nas equações
(28), (29), (35), e (36) é possível encontrar os valores
das matrizes , , , , e . Então, utilizando as equações (9) e (37) é possível encontrar os
valores da matriz . A Matriz pode encontrada
através de:
1 ". '9
:.. /
1 " (39)
Utilizando a ferramenta rltool do Matlab, o lugar
das raízes do sistema é apresentado na Figura 5.
3.2 Projeto do Controlador PI
8
0.07111 533.3
6.684. 10#? . 0.0001333. 1
8.611. 10#? . 0.002481 1.181
0.000539. 0.7707. 1
(40)
Para a simulação, alguns pontos devem ser levados em consideração. Primeiramente a realimentação
do sistema deve ser feita utilizando um transdutor de
tensão para a medição da tensão de saída e a representação de uma tensão de referência no controlador.
Outra consideração é que o controlador deverá compensar quando houver variação na tensão de entrada.
Então, o valor da tensão de entrada também será
fornecido ao controlador. Assim, a Figura 6 representa o sistema que será simulado.
(38)
Enfim, utilizando a equação (21) é possível encontrar a função de transferência do conversor.
Para validar a eficiência do controlador neural
no projeto, a função de transferência utilizada no
3747
Anais do XX Congresso Brasileiro de Automática
Belo Horizonte, MG, 20 a 24 de Setembro de 2014
vO*
VO
D
1
VS
C ( s)
Na Figura 9, é possível observar um erro em regime permanente. Isso porque o controlador foi projetado para uma tensão de entrada maior que a usada
nesta simulação. Uma melhor visualização dessa
condição pode ser observada na Figura 10, onde a
tensão de entrada é de 90V.
G (s)
Hc
500
Figura 6. Diagrama de blocos do sistema com sinal de erro de
tensão de entrada.
Vin
Vout
Tensão (V)
400
O bloco representa a função de transferên
cia do controlador. O bloco representa o ganho do
controlador, onde C 400. O bloco & representa
a função de transferência do conversor. O bloco DE
representa o ganho sensor de tensão e possui um
valor de DE 0.1. O conversor está conectado a uma
carga resistiva com valor de '( 53.333F, que
permite ao sistema entregar 3kW de potência. A
saída do controlador é a razão cíclica ".
A simulação permitiu a validação através da observação da tensão de saída para diferentes tensões
de entrada. Assim, a Figura 7 apresenta a resposta do
sistema para uma entrada de 300V.
0
0
Tensão (V)
400
300
200
100
0.15
0.2
0.25
0.15
0.2
0.25
0.3
É possível observar que o comportamento do
controlador não consegue atuar de forma satisfatória
para todo ponto de operação do circuito. Assim, para
valores de entrada diferentes da tensão utilizada para
a obtenção dos valores do controlador, o sistema
continua controlando, mas apresenta maior oscilação
na tensão de saída, além de diferentes tempos de
assentamento e estabilização da mesma.
Isso comprova a necessidade de projetar um controlador capaz de se adaptar às diferentes tensões de
entrada do sistema e que será projetada para avaliação e validação da proposta do trabalho.
Para o desenvolvimento de uma rede neural capaz de substituir o controle convencional desenvolvido no conversor, o primeiro procedimento é coletar
informações de operação para que esses dados possam servir para o treinamento da rede neural.
Para a correta substituição do controlador convencional pelo neural, este deve ser treinado com as
mesmas condições do controlador convencional, ou
seja, utilizando como sinal de entrada a tensão de
entrada e de saída e, como saída, a razão cíclica. Para
o treinamento da rede neural, um conjunto de informações foi coletado, a partir da simulação do sistema
com controle convencional. Para o treinamento e
validação, foram coletadas informações conforme a
Tabela 2.
Vin
Vout
0.1
0.1
Figura 10. Tensão de saída do conversor para entrada de 90V.
500
0.05
0.05
Tempo (s)
700
0
0
200
100
AB
600
300
0.3
Tempo (s)
Figura 7. Tensão de saída do conversor para entrada de 300V.
A tensão de saída é de 400V conforme desejado,
ocorrendo uma oscilação em regime permanente.
Isso se deve ao fato de que, propositalmente, não foi
executado o projeto do controlador utilizando a função de transferência considerando a resistência interna do indutor e da chave de potência. A Figura 8 e 9
apresentam, respectivamente, a tensão de saída para
uma tensão de entrada de 200V e 120V.
700
Vin
Vout
600
Tensão (V)
500
Tabela 2. Especificações para projeto do controlador PI de tensão.
400
300
Tensão de entrada
200
Tempo
Amostras
(cada entrada)
(cada entrada)
0,2s
20.000
100
0
0
0.05
0.1
0.15
0.2
0.25
0.3
Tempo (s)
90V a 350V, com
passos de 20V
Figura 8. Tensão de saída do conversor para entrada de 200V.
Foram executadas 14 simulações, com tensão de
entrada inicial de 90V até 350V, com passos de 20V.
O tempo de execução de cada treinamento foi de
0,2s, pois para todas as entradas, esse tempo era o
suficiente para que o sistema operasse no modo dinâmico e operasse um período regime permanente,
permitindo que os dados contivessem informações
para os dois modos. A taxa de amostragem utilizada
foi de 10#G . Assim, cada amostra coletada gerou
600
Vin
Vout
Tensão (V)
500
400
300
200
100
0
0
0.05
0.1
0.15
0.2
0.25
0.3
Tempo (s)
Figura 9. Tensão de saída do conversor para entrada de 120V.
3748
Anais do XX Congresso Brasileiro de Automática
Belo Horizonte, MG, 20 a 24 de Setembro de 2014
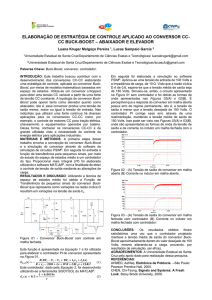
A curva em azul representa a tensão de entrada
do sistema. A curva em preto representa a tensão de
saída do conversor controlado pelo PI convencional.
A curva em vermelho representa a tensão de saída do
conversor controlado pelo controlador neural.
uma matriz de três linhas por 20.000 colunas. As
linhas representam, respectivamente, a tensão de
entrada, tensão de saída e a razão cíclica. As amostras foram organizadas conforme a Tabela 3.
1000
Tabela 3. Amostras para rede neural.
Vin
PI Convencional
PI Neural
Tipo de amostra
Quantidade
Amostra para
treinamento
Amostra para
validação
Tensão (V)
800
Tamanho de
cada matriz
(mxn)
02
0
0
0.1
0.15
0.2
0.25
0.3
Figura 11. Resposta do sistema para uma tensão de entrada de
300V.
Observando a curva vermelha, é possível perceber que o tempo de subida utilizando o controle é
bem menor. O sobressinal para esse caso também é
menor. Com o PI convencional, a tensão de pico
alcançou valores próximos a 880V, enquanto que no
controle neural a tensão de pico é de aproximadamente 680V. O tempo de estabilização da saída utilizando do controle neural é menor. Além disso, é
possível perceber que o funcionamento em regime é
melhor, uma vez que a oscilação na tensão de saída é
menor. Então, pode-se concluir que o controle neural
trouxe uma melhoria na resposta do sistema em relação ao controle PI convencional. Ressaltando que a
tensão de 300V de entrada não fazia parte do grupo
de dados utilizados no treinamento da rede. Por isso,
além de trazer a melhora na resposta do sistema,
pode-se concluir também que a rede está sendo capaz
de generalizar sua saída para valores de tensão de
entrada que não foram utilizados no treinamento.
Isso mostra a robustez do sistema para variações de
tensões de entrada, sobretudo nesse caso em que a
resposta da tensão de saída foi melhor que a resposta
do sistema controlado pelo sistema convencional.
Para a validação completa do sistema, outras simulações foram executadas considerando diferentes
tensões de entrada. A Figura 12 apresenta a resposta
do sistema para uma tensão de entrada de 100V.
Tabela 4. Amostras para rede neural.
PMC
2
10
1
3.10#H
LevenbergMarquardt
672
52m:13s
Tangente hiperbólica
Rampa simétrica
600
Vin
PI Convencional
PI Neural
500
Tensão (V)
Épocas de convergência
Tempo de convergência
Função de ativação (camada
intermediária)
Função de ativação (camada
de saída)
Matriz de treinamento
Matriz de validação
0.05
Tempo (s)
Como a busca da rede neural é uma saída que
representa uma função, a topologia escolhida para
esse projeto é a Rede Perceptron Multicamadas.
Como a rede trabalhará com duas entradas, ela possui
uma camada de entrada, composta por 2 neurônios.
A saída dessa rede é composta por um neurônio. O
computador utilizado para a simulação possui um
processador Core2Duo com velocidade de 1.8GHz e
memória RAM de 4Gb. A Tabela 4 apresenta as
informações referentes à rede.
Topologia da rede
Neurônios na camada de
entrada
Neurônios na camada
intermediária
Neurônios na camada de saída
Tolerância de erro
Método de otimização
400
200
3x20.000
cada
3x20.000
cada
12
600
3x2.400.000
3x40.000
400
300
200
100
0
0
Após o processo de aprendizagem, uma matriz
contendo todos os pesos relacionados a cada neurônio foi encontrado. Então, foi possível desenvolver,
através do software Matlab/Simulink uma simulação
da rede neural. O treinamento e a simulação da rede
neural foram executados utilizando a toolbox Neural
Network presente no Matlab/Simulink. A rede neural,
trabalhando como controle neural, atuou fornecendo
a razão cíclica para o conversor. A primeira simulação consiste em verificar a resposta do sistema com a
tensão de entrada de 300V. Dessa forma, a Figura 11
apresenta a resposta do sistema para essa tensão de
entrada.
0.05
0.1
0.15
0.2
0.25
0.3
Tempo (s)
Figura 12. Resposta do sistema para uma tensão de entrada de
100V.
As cores azul, preto e vermelho das curvas representam a mesma grandeza da figura anterior. Este
ponto de operação é interessante, pois o controlador
convencional está operando em uma situação de
grande perturbação, já que a tensão de entrada é de
apenas 1/3 da tensão na qual o controlador foi projetado. A consequência disso é que o sistema, além de
oscilante, não alcança a tensão nominal de saída,
ocasionando um erro em regime permanente. O con3749
Anais do XX Congresso Brasileiro de Automática
Belo Horizonte, MG, 20 a 24 de Setembro de 2014
nal não conseguiu. Além disso, se mostrou melhor no
tempo de resposta, melhor resposta em regime permanente e menor sobressinal do transitório de partida. Dessa forma, a proposta foi alcançada e o controlador baseado na teoria de redes neurais pode substituir o controlador convencional com vantagens.
O controlador neural é capaz de operar como um
eficiente controle adaptativo e ainda é capaz de operar trazendo melhoria em relação ao controle convencional.
trolador neural, por sua vez, se adapta melhor a esse
ponto de operação e consegue uma resposta muito
melhor do que a resposta do controlador convencional, com relação ao erro em regime e oscilação na
tensão de saída.
Outra tensão escolhida para a validação desse
controlador foi a tensão de entrada de 340V. Esta
tensão foi escolhida, pois assim como a tensão de
operação do caso anterior, também apresenta uma
tensão de trabalho próxima ao limite de operação.
Nesse caso, o limite de máxima tensão de entrada do
conversor, como mencionado, é de 350V. Entretanto,
esse valor de tensão foi utilizado no treinamento da
rede. Logo, a tensão de 340V representa esse ponto
crítico de operação, e também a capacidade da rede
de generalizar sua saída. Dessa forma, a Figura 13
apresenta a resposta do sistema validando assim o
controle e a generalização da rede neural.
Referências Bibliográficas
Erickson, R. W. and Maksimović, D. (1994).
Fundamentals of Power Electronics. 2. ed.
Colorado: Kluwer, 2001.
Hassam, M.Y. and Kothapalli, G. (2010).
Comparison between Neural Network based PI
and PID controllers. Systems Signals and
Devices (SSD), 2010 7th International MultiConference on , vol., no., pp.1,6, 27-30 June
2010.
Kaboli, S.H.A. and Mansouri, M. and Selvaraj, J. and
Rahim, N.B.A. (2013). A hybrid adaptive
Neural-Fuzzy tuned P.I. controller based
Unidirectional Boost P.F.C. converter feeds
B.L.D.C. drive. Power Electronics, Drive
Systems
and
Technologies
Conference
(PEDSTC), 2013 4th , vol., no., pp.176,181, 1314 Feb. 2013.
Kothapalli, G and Hassan, M. Y. (2008). Design of a
Neural Network based intelligent PI controller
for a pneumatic system. IAENG International
Journal of Computer Science 01/2008 IJCS,
2008.
Mahdavi, J. and Nasiri, M. R. and Agah, A. and
emadi, A. (2005). Application of neural
networks and state-space averaging to DC/DC
PWM converters in sliding-mode operation.
IEEE Transaction on Mechatronics, vol. 10,
No.1. pp. 60 - 67, February 2005.
Pomilio, J. A. (2014). Fontes Chaveadas. Apostila Universidade Estadual de Campinas, Campinas,
SP, 2014.
Utomo, W.M. and Bakar, A. and Ahmad, M. and
Taufik, T. and Heriansyah, R. (2013). Online
Learning Neural Network Control of BuckBoost Converter. Information Technology: New
Generations (ITNG), 2011 Eighth International
Conference on , vol., no., pp.485,489, 11-13
April 2011 4th Power Electronics, Drive
Systems
&
Technologies
Conference
(PEDSTC2013), Feb l3-14, 2013, Tehran, Iran.
1000
Vin
PI Convencional
PI Neural
Tensão (V)
800
600
400
200
0
0
0.05
0.1
0.15
0.2
0.25
0.3
Tempo (s)
Figura 13. Resposta do sistema para uma tensão de entrada de
340V.
Percebe-se que a tensão de pico para o conversor
neural é menor, assim como o tempo de subida e o
tempo de assentamento. Outra observação é que o
erro em regime permanente é pequeno, além de não
apresentar uma oscilação na tensão de saída.
3 Conclusão
Este artigo apresentou o estudo, projeto e simulação de um conversor CC-CC tipo boost que será
aplicado a um sistema de conversão de energia eólica
para a produção de energia elétrica. A utilização do
conversor para estabilizar a tensão de saída é vital
para que o sistema possa servir como fonte de alimentação de cargas. Foi estudado e comprovado
através de simulações que um controle pode ser projetado para controlar o conversor. Entretanto, este
controle opera de forma otimizada apenas em uma
faixa de operação, trazendo resultados insatisfatórios
para outras faixas de operação. Portanto, a necessidade de um sistema de controle adaptativo é uma
solução para este problema.
A proposta foi utilizar um sistema de controle
neural, capaz de aprender os melhores pontos de
operação do sistema, buscando um funcionamento
adequado para todas as faixas de operação.
O controle proposto atendeu as expectativas e
mostrou-se como uma solução para o problema. Ele
foi capaz de substituir de forma completa o controlador convencional e trouxe uma excelente resposta
para as faixas de operação que o sistema convencio-
3750