Cálculo dos Predicados

11/04/2011
Cálculo dos Predicados

As sentenças assim formuladas foram
chamadas de proposições categóricas e,
segundo Aristóteles, podem ser de 4 tipos:
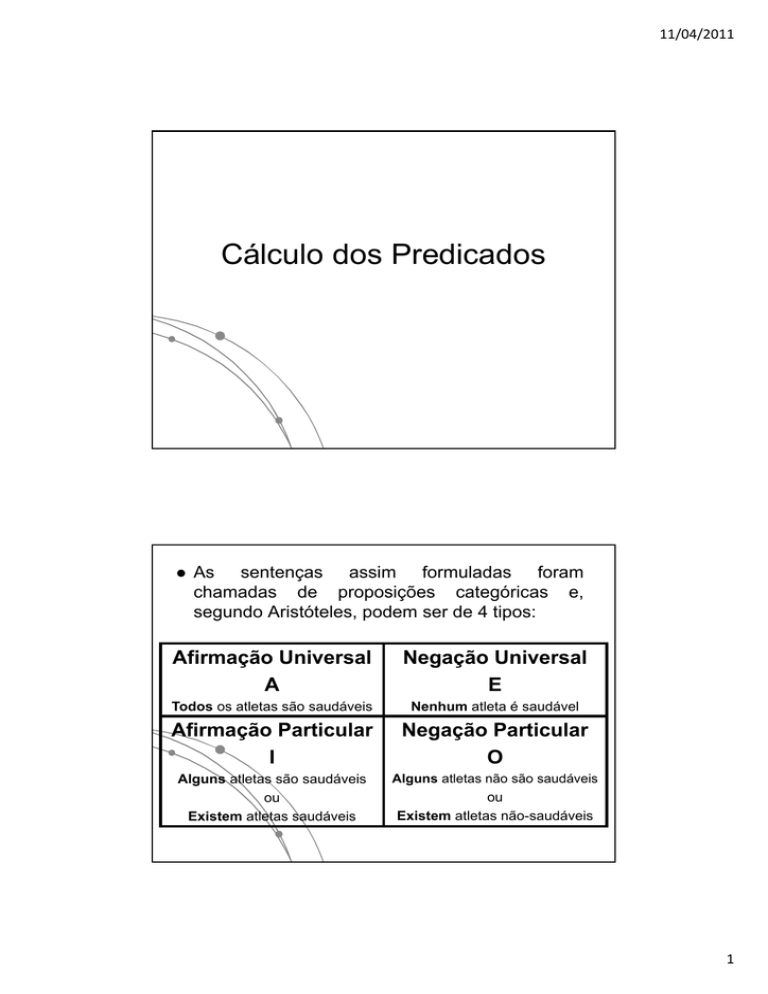
Afirmação Universal
A
Negação Universal
E
Todos os atletas são saudáveis
Nenhum atleta é saudável
Afirmação Particular
I
Negação Particular
O
Alguns atletas são saudáveis
ou
Existem atletas saudáveis
Alguns atletas não são saudáveis
ou
Existem atletas não-saudáveis
1
11/04/2011
Quantificador Existencial
Exemplo:
Existe uma pessoa chamada Pedro.
 x pessoa(x) ^ nome(x, Pedro)
Quantificadores
Exemplos:
Todo
homem é mortal, ou seja,
qualquer que seja x (do Universo),
se x é Homem, então x é Mortal.
 x (H(x)→M(x)).
2
11/04/2011
Quantificadores
Exemplos:
Nenhum
homem é vegetal, ou
sejam qualquer que seja x, se x é
Homem, então x NÃO É Vegetal.
 x (H(x)→~V(x)).
Quantificadores
Exemplos:
Pelo
menos um homem é
inteligente, ou seja, existe pelo
menos um x em que x seja
Homem e x seja Inteligente.
 x(H(x) ^ I(x))
3
11/04/2011
Cálculo de Predicados

Sintaxe do Cálculo de Predicados
 Fórmulas Atômicas:
 É uma letra predicativa, seguida por zero
ou mais letras nominais ou variáveis.
 Fórmulas Bem Formadas:
 Uma Fórmula Atômica é uma Fórmula
Bem Formada;
 Se P é uma fbf, então ~P também o é;
 Se P e Q são fbfs, então (P ^ Q), (P v Q),
(PQ), (PQ) também o são;
 Se P(x) é uma fbf, então x(P(x)) e
x(P(x)) também o são
Cálculo de Predicados

Ex.: Seja P = F(a) ^ G(a,b),
então são fbfs:
x(F(x) ^ G(a,b))
x(F(x) ^ G(x,b))
x(F(a) ^ G(a,x))
x(F(x) ^ G(a,b))
4
11/04/2011
Cálculo de Predicados

Regras de Inferência para o Cálculo de
Predicados

Todas as regras definidas no Cálculo
Proposicional continuam válidas no Cálculo de
Predicados, apenas referenciando-as para os
quantificadores.
Ex.: ~F(a) v xF(x), xF (x)P ]- F(a) P.
Prova:
1.
~F(a) v xF(x)
Premissa

Cálculo de Predicados
Ex.: ~F(a) v xF(x), xF (x)P ]- F(a) P.
Prova:
1.
~F(a) v xF(x)
Premissa
2.
xF (x)P
Premissa
3.
F(a)
Hipótese
4.
~~F(a)
3 DN
5.
xF(x)
1,3 SD
6.
P
2,5 MP
7.
F(a) P
3,6 PC

5
11/04/2011
Cálculo de Predicados

Regras de Inferência para o Cálculo
de Predicados

1.
2.
3.
4.
Intercâmbio de Quantificadores
~(x ~F(x)) =
xF(x)
~(x F(x)) =
x~F(x)
x ~F(x) =
~(xF(x))
x F(x)
=
~(x~F(x))
Exercício:

Para formalizar os argumentos que
seguem, Interprete as letras C, R, V e S
como:
C  está chovendo;
R  é uma rã;
V  é verde;
S  é saltitante;
12
6
11/04/2011
Exercícios
a) Todas as rãs são
verdes.
b) Nenhuma rã é verde.
c) Algumas rãs são verdes.
d) Algumas rãs não são
verdes.
e) Toda coisa é uma rã.
f) Alguma coisa é uma rã.
g) Nem toda coisa é uma
rã.
h) Nada é uma rã.
i) Existem rãs verdes.
Exercícios
i)Existem rãs verdes
j) Qualquer coisa ou é
verde ou é iridescente.
k) Qualquer coisa é uma rã
verde.
l) Está chovendo e
algumas rãs estão
saltitando.
m) Se está chovendo,
então todas as rãs estão
saltitando.
.
7
11/04/2011
Exercícios
n) Algumas coisas são
verdes e algumas não são.
o) Algumas coisas são
verdes e iridescentes
simultaneamente.
p) Ou qualquer coisa é
uma rã ou nada é uma rã.
q) Qualquer coisa ou é
uma rã ou não é uma rã.
r) Todas as rãs são rãs.
s) Somente rãs são verdes.
Exercício 2:

Para formalizar os argumentos que seguem considere a
interpretação:
Indivíduos:
Carlos, João e Maria
Predicados:
Mecânico(x)  x é mecânico
Enfermeiro(x)  x é enfermeiro
Ama(x, y)  x ama y
16
8
11/04/2011
Exercício 2:
1) Carlos é mecânico
Mecânico(Carlos)
2) Carlos e João são mecânicos
Mecânico(Carlos) ^ Mecânico(João)
3) Carlos é mecânico ou enfermeiro
Mecânico(Carlos) v Enfermeiro(Carlos)
17
Exercício 2:
4) Se Carlos é mecânico então Carlos não é
enfermeiro
Mecânico(Carlos)  ~Enfermeiro(Carlos)
5) João ama Maria
Ama(João, Maria)
6) João ama a si próprio
Ama(João, João)
18
9
11/04/2011
Exercício 2:
7) Todo mundo ama João
x(Ama(x, João))
8) Existe alguém que Maria não ama
x(~Ama(Maria, x))
9) Todo mundo é amado por alguém
xy(Ama(y, x))
19
Exercício 2:
10) Alguém é amado por todos
xy(Ama(y,x))
11) Existe alguém que ama todo
mundo
xy(Ama(x,y))
12) Alguém ama alguém
xy(Ama(x,y))
20
10
11/04/2011
Exercício 3: EXPRESSÕES TEXTUAIS
MOSTRANDO FORMAS LÓGICA E SIMBÓLICA:
um quantificador e predicados monádicos

Não existem marcianos (M(x)  x é marciano)
(não existe x tal que x seja um marciano)
 x M(x)
( ou
para todo x, x não é um marciano)
x ( M(x))
21
Exercício 3: EXPRESSÕES TEXTUAIS
MOSTRANDO FORMAS LÓGICA E SIMBÓLICA:
um quantificador e predicados monádicos

Nem todos são sábios (S(x)  x é sábio)
(para nem todo x, x é sábio )
 x S(x)
(ou existe um x tal que x não é sábio)
x ( S(x))
22
11
11/04/2011
Exercício 3: EXPRESSÕES TEXTUAIS
MOSTRANDO FORMAS LÓGICA E SIMBÓLICA:
um quantificador e predicados monádicos

Os morcegos são mamíferos (C(x)  x é
morcego; M(x)  x é um mamífero)
(para todo x, se x é um morcego, x é um
mamífero)
x (C(x)  M(x))
23
Exercício 3: EXPRESSÕES TEXTUAIS
MOSTRANDO FORMAS LÓGICA E SIMBÓLICA:
um quantificador e predicados monádicos

Os cavalheiros não são sempre ricos
(para nem todo x, se x é um cavalheiro então
x é rico)
 x (C(x)  R(x))
(ou, existe um x tal que x é um cavalheiro e x
não é rico)
x (C(x)   R(x))
24
12
11/04/2011
Exercício 3: EXPRESSÕES TEXTUAIS
MOSTRANDO FORMAS LÓGICA E SIMBÓLICA:
um quantificador e predicados monádicos

Somente os médicos podem cobrar por
tratamento clínico
(para todo x, se x pode cobrar por
tratamento clínico, então x é médico)
x (C(x)  M(x))
25
Exercício 3: EXPRESSÕES TEXTUAIS
MOSTRANDO FORMAS LÓGICA E SIMBÓLICA:
um quantificador e predicados monádicos

Os carros são seguros somente se
tiverem bons freios
(para todo x, se x é um carro, então x é
seguro somente se tiver bons freios)
x [ C(x)  (S(x)  F(x)) ]
26
13
11/04/2011
Exercício 3: EXPRESSÕES TEXTUAIS
MOSTRANDO FORMAS LÓGICA E
SIMBÓLICA:
mais de um quantificador e predicados
monádicos

Alguns são espertos, outros não
(existe x tal que x é esperto, e existe y
tal que y não é esperto)
x E(x)  y ( E(y))
27
Exercício 3: EXPRESSÕES TEXTUAIS
MOSTRANDO FORMAS LÓGICA E
SIMBÓLICA:
mais de um quantificador e predicados
monádicos

Existem políticos honestos e
desonestos
(existe x tal que x é político e x é
honesto, e existe y tal que y é político e
y não é honesto)
x (P(x)  H(x))  y (P(y)   H(y))
28
14
11/04/2011
Exercício 3: EXPRESSÕES TEXTUAIS
MOSTRANDO FORMAS LÓGICA E SIMBÓLICA:
Relações

Todos têm pai
(F(x,y) : x é pai de y)
(para todo x existe y tal que y é pai de x)
x y F(y,x)

Todas as pessoas têm pai
(para todo x, se x é uma pessoa, existe y tal que y é
pai de x)
x (P(x)  y F(x,y))
29
Exercício 3: EXPRESSÕES TEXTUAIS
MOSTRANDO FORMAS LÓGICA E SIMBÓLICA:
Relações

Existe um ancestral comum a todas as
pessoas
(existe um x tal que para todo y, se y é uma
pessoa, x é ancestral de y)
x y (P(y)  A(x,y))
(ou, para todo y, se y é uma pessoa, existe
um x tal que x é ancestral de y)
y (P(y)  x A(x,y))
30
15
11/04/2011
Exercício 3: EXPRESSÕES TEXTUAIS
MOSTRANDO FORMAS LÓGICA E SIMBÓLICA:
Relações estabelecendo regras de parentesco
 Genro
se x é casado com a filha de y, então x é genro
de y;
ou, mais precisamente: se existir z tal que x seja
casado com z, e z seja filha de y, então x é
genro de y
x y [ z (C(x,z)  F(z,y))  G(x,y) ]
31
Exercício 3: EXPRESSÕES TEXTUAIS
MOSTRANDO FORMAS LÓGICA E SIMBÓLICA:
Relações estabelecendo regras de parentesco

Avô
se x é pai do pai de y, então x é avô de y
x y [ z (P(x,z)  P(z,y))  A(x,y) ]
32
16
11/04/2011
Exercício 3: EXPRESSÕES TEXTUAIS
MOSTRANDO FORMAS LÓGICA E SIMBÓLICA:
Relações estabelecendo regras de parentesco

Irmão
se o pai de x for também pai de y, x é
irmão de y
x y [ z (P(z,x)  P(z,y))  I(x,y) ]
33
Lógica de Predicados. Exemplo
Considere o seguinte conjunto de frases:
1. Marcos é um homem.
2. Marcos é brasileiro.
3. Lula é presidente
4. Todos os brasileiros são leais a Lula ou odeiam
Lula.
5. Os brasileiros vaiam presidentes a quem não sejam
leais.
6. Marcos vaiou o Lula.
17
11/04/2011
Lógica de Predicados. Exemplo
Estes fatos podem ser representados como
1. homen(Marcos)
2. brasileiro(Marcos)
3. presidente(Lula)
4.  x brasileiro(x)  leal(x,Lula) v odeia(x,Lula)
5.  x  y brasileiro(x) ^ presidente(y) ^ vaia(x,y) 
~leal(x,y)
6. vaia(Marcos, Lula).
Cuidados na Formalização:
1) Variáveis diferentes não classificam
necessariamente objetos diferentes.
Ex.: xy ama(x, y)
Afirma não somente que qualquer
pessoa ama uma outra pessoa, como
também que qualquer pessoa ama a si
própria.
36
18
11/04/2011
Cuidados na Formalização:
2) O nome de variáveis não faz diferença
para o significado.
Ex.: xy ama(y, x) equivale a
yx ama(x, y) equivale a
zw ama(w,z)
37
Cuidados na Formalização:
3) Quando dois ou mais quantificadores
justapõem-se numa mesma parte da
fórmula, uma variável diferente deve ser
usada para cada quantificador.
Ex.: xx ama(x, x) não é correto
xy ama(y, x) é correto
38
19
11/04/2011
Cuidados na Formalização:

4) A mesma variável usada em vários
quantificadores, não designa
necessariamente o mesmo objeto em
cada caso.
Ex.: x ama(josé, x) ^ x ama(carlos, x)
39
Cuidados na Formalização:

5) A ordem dos quantificadores consecutivos
afeta o significado somente quando os
quantificadores são diferentes.
Ex.:
xy ama(x,y) e yx ama(x,y)
tem significados distintos
xy ama(x,y) e
yx ama(x,y)
significam a mesma coisa
40
20
11/04/2011
Cuidados na Formalização:

6) Os advérbios só, somente e apenas tem significados diferentes
dependendo do local em que aparecem na sentença. Representam uma
implicação e o conseqüente sempre aparece depois do advérbio.
Sentença
Significado
João ama apenas Maria
Se João ama alguma coisa, essa coisa é
Maria
Apenas João ama Maria
Se alguma coisa ama Maria, essa coisa é
João
João apenas ama Maria
Se João tem alguma relação com Maria, essa
relação é amor
41
Cuidados na Formalização:










6.1) Exemplos usando esses adverbios:
Apenas cachorros perseguem gatos
x(G(x)  y( P(y,x)  C(y)))
ou
xy((G(x) ^ P(y,x))  C(y))
Cachorros perseguem apenas gatos
x y((C(x) ^ P(x,y))  G(y))
Só os diamantes brilham
x (B(x)  D(x))
Diamantes só brilham
x (D(x)  B(x))
42
21
11/04/2011
Revisão: O Diagrama de Venn e o SC




Para a Proposição Universal Afirmativa (A) “Todo S é P”,
x (Sx  Px) temos o 1o diagrama;
Proposição Universal Negativa (E), “Nenhum S é P”, ou,
simbolicamente, x (Sx  ~Px), pelo 2o;
A Proposição Particular Afirmativa (I), “Algum S é P”, ou x (Sx
 Px), é representada pelo 3o diagrama abaixo;
Proposição Particular Negativa (O), “Algum S não é P”, cuja
forma simbólica é x (Sx  ~Px),
A
I
E
O
Eliminação e Inserção de Quantificadores
As quatro regras geradas são chamadas de:
Generalização
Universal
Existencial;
Instanciação Universal e Existencial;

22
11/04/2011
Eliminação Universal (EU)
“Se todos os objetos de um dado universo possuem uma
dada propriedade, então um objeto particular desse
universo também possui essa propriedade”.

Esta regra estabelece que o que é verdade para qualquer
indivíduo deve ser verdade para um indivíduo particular
Generalização Universal (GU)
“Se um objeto, arbitrariamente escolhido dentre um
universo, tiver uma certa propriedade, todos os objetos
desse universo terão essa propriedade”.

Esta regra estabelece que se pudermos provar algo a respeito
de uma indivíduo b sem fazer suposição que distinga b de um
outro indivíduo, então o que tivermos provado para b estará
provado para todos.
23
11/04/2011
Generalização Existencial (GE)
“O que é verdadeiro para um dado objeto, é verdadeiro para
algum objeto”.
Instanciação Existencial (IE)
“O que é verdadeiro para algum objeto, é verdadeiro para um
dado objeto, desde que esse objeto não tenha sido utilizado
anteriormente na dedução”.
24
11/04/2011
Dedução no CP: Exemplo
Nenhum atleta é apegado aos livros.
Carlos é apegado aos livros.
Portanto, Carlos não é um atleta.
Sol: x (Ax   Lx)
L (Carlos)
  A (Carlos)
Dedução no CP: Exemplo
2. Ácidos ou bases são químicos.
O vinagre é um ácido.
Logo, o vinagre é um químico.
Sol:
x(AxBx  Qx)
A (vinagre)
 Q (vinagre)
25
11/04/2011
Exemplos de dedução
3. Todos os cidadãos que
não são traidores estão
presentes.
Todos os oficiais são
cidadãos.
Alguns oficiais não
estão presentes.
Logo, há traidores.
Sol:
x (Cx TxPx)
x (Ox  Cx)
x (Ox   Px)
 x Tx
Ver mais ex. na pp. 71.
Validade e Subargumentos


Se o número de premissas e/ou de predicados em um
argumento é grande, a dificuldade em deduzir a conclusão ou de
provar a invalidade do argumento cresce significativamente.
Nestes casos, o uso de subargumentos é recomendável. Ele
consiste em:
1. escolher uma ou mais premissas no argumento dado;
2. obter uma conclusão com essas premissas, construindo um
subargumento válido;
3. incluir a conclusão obtida como mais uma premissa no
argumento original.
Repetir o processo até se obter a conclusão do argumento
original, ou ficar convencido de que isso não será possível.
26
11/04/2011
Validade: uso de
subargumentos
Exemplo: Alguns fotógrafos são habilidosos.
Só artistas são fotógrafos. Os fotógrafos não
são todos habilidosos. Todo biscateiro é
habilidoso. Logo, alguns artistas não são
biscateiros.
Sol: a 3a e 4a premissas escritas na forma típica:
Todo biscateiro é habilidoso.Alguns fotógrafos não
são habilidosos. Logo, alguns fotógrafos não são
biscateiros. (silogismo categórico).
Sol: Forma simbólica
x (Bx  Hx) (A),
x (Fx   Hx) (O);
 x (Fx   Bx)
O diagrama de Venn ao lado valida o subargumento:
Validade: uso de
subargumentos
Substituindo as premissas pela conclusão, e
escrevendo a outra premissa na forma típica,
temos o outro argumento como outro
silogismo categórico:
Todos os fotógrafos são artistas.
Alguns fotógrafos não são biscateiros.
Logo, alguns artistas não são biscateiros.
Sol: Forma simbólica:
x (Fx  Ax) (A),
x (Fx   Bx) (O);
 x (Ax   Bx)
O diagrama de Venn ao lado valida o argumento:
(ver outro exemplo na pag 75) .
27
11/04/2011
Conectivos temporais










Igualdade
Começam juntos:
Acabam juntos:
é anterior a
é posterior a
é seguido por
segue
contém
é contido em
contém momento simultâneo
28