Aula 06 - Solução

Aula 06
ASSUNTOS: Circuitos elétricos de corrente contínua; potência elétrica; leis de OHM; efeito Joule.
1.
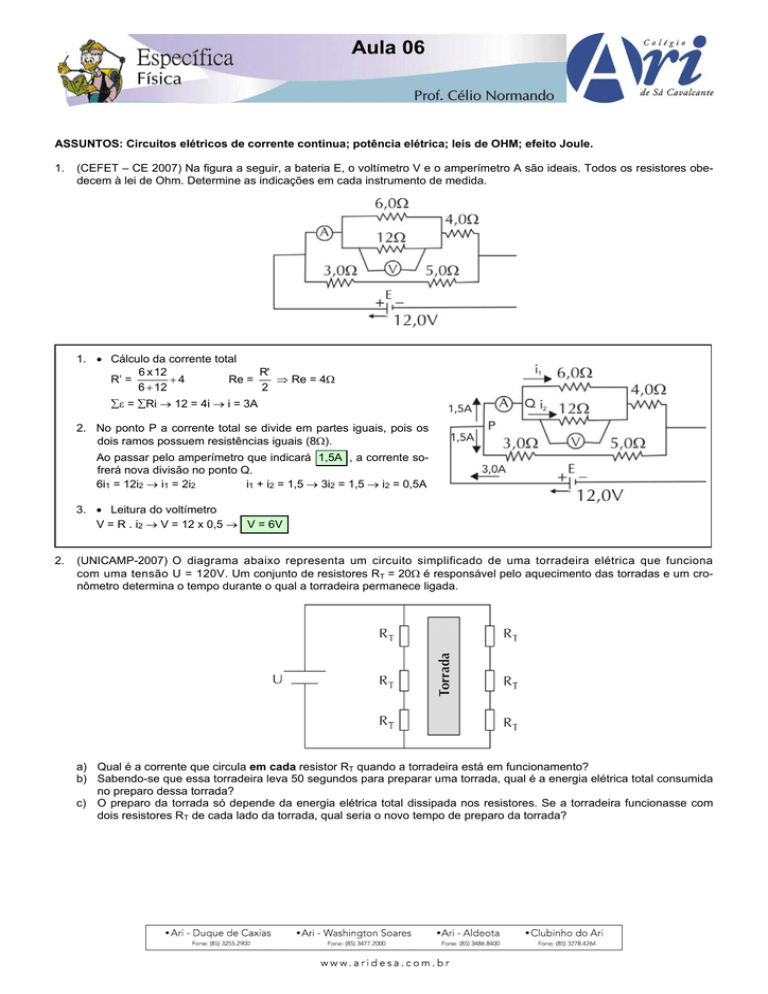
(CEFET – CE 2007) Na figura a seguir, a bateria E, o voltímetro V e o amperímetro A são ideais. Todos os resistores obedecem à lei de Ohm. Determine as indicações em cada instrumento de medida.
1. • Cálculo da corrente total
6 x12
R'
R’ =
+4
Re =
⇒ Re = 4Ω
6 + 12
2
∑ε = ∑Ri → 12 = 4i → i = 3A
2. No ponto P a corrente total se divide em partes iguais, pois os
dois ramos possuem resistências iguais (8Ω).
Ao passar pelo amperímetro que indicará 1,5A , a corrente sofrerá nova divisão no ponto Q.
i1 + i2 = 1,5 → 3i2 = 1,5 → i2 = 0,5A
6i1 = 12i2 → i1 = 2i2
3. • Leitura do voltímetro
V = R . i2 → V = 12 x 0,5 → V = 6V
2.
(UNICAMP-2007) O diagrama abaixo representa um circuito simplificado de uma torradeira elétrica que funciona
com uma tensão U = 120V. Um conjunto de resistores RT = 20Ω é responsável pelo aquecimento das torradas e um cronômetro determina o tempo durante o qual a torradeira permanece ligada.
a) Qual é a corrente que circula em cada resistor RT quando a torradeira está em funcionamento?
b) Sabendo-se que essa torradeira leva 50 segundos para preparar uma torrada, qual é a energia elétrica total consumida
no preparo dessa torrada?
c) O preparo da torrada só depende da energia elétrica total dissipada nos resistores. Se a torradeira funcionasse com
dois resistores RT de cada lado da torrada, qual seria o novo tempo de preparo da torrada?
Aula 06
a) No ramo esquerdo da torradeira
U = 120V
Re = 3RT
U = Re . i → 120 = 60i → i = 2A
b) A potência total dissipada no circuito é:
P = 6 . RT . i2 → P = 6 . 20 . 22 ∴ P = 480W
Mas P =
∆ε
∆ε
∴
→ 480 =
∆t
50
∆ε = 24000J
c) A potência total dissipada é:
U2
∆ε
P=
P=
∆t
Re
Na situação inicial
3RT
U2
3RT ∆ε
∆ε
Re =
→
=
→ ∆t 1 =
3RT
2
∆t 1
2U2
2
Na situação final
2RT
U2
R ∆ε
∆ε
Re =
→
=
→ ∆t 2 = T 2
2RT
2
∆t 2
U
2
RT ∆ε
∆t 2
2U2
2
2
x 50
¨ ∴ ∆t2 =
∆t1 → ∆t2 =
=
x
2
3
3
3RT ∆ε
∆t 1
U
∆t2 ≅ 33,3s
3.
(UNESP-2007) Como conseqüência do rápido desenvolvimento da tecnologia eletrônica, hoje é possível realizar experimentos nas diversas áreas da ciência utilizando amostras com dimensões da ordem nm (1nm = 10–9m). Novas perspectivas foram introduzidas e vêm sendo exploradas, como as investigações sobre propriedades elétricas de macromoléculas e
cadeias poliméricas, como as proteínas. Diante dessa possibilidade, um pesquisador verificou com sucesso a sua hipótese
de que uma determinada proteína, esticada, satisfazia à lei de Ohm. Depois de medidas sistemáticas da resistência elétrica, ele concluiu que o seu valor é R. Prosseguindo na investigação, partiu essa cadeia em dois pedaços, ligando-os em
3R
paralelo, e a medida da resistência efetiva foi de
. Considerando que o pedaço de menor comprimento tenha resistên16
cia R1 e o de comprimento maior, resistência R2, calcule esses valores expressos em termos de R.
•
R1 + R2 = R (α)
⇒ R1R2 =
•
RR
3R
1 2
=
R1 + R2
16
3 2
R
16
(γ)
(β)
Substituindo (γ) em (α):
3R2
+ R2 = R ∴ 16R22 – 16RR2 + 3R2 = 0
16 . R2
R2 =
4.
16R ±
R
3R

 R2 = 4 ⇒ R1 = 4
(16) R − 4.16.3R 
 ou
2 . 16

3R
R
 R2 =
⇒ R1 =
4
4

2
2
2
(UFRN-2007) Para montar um circuito elétrico, você dispõe de uma bateria de automóvel de 12V e de quatro lâmpadas
incandescentes, sendo duas do tipo L1 e duas do tipo L2, com as especificações nominais indicadas na figura abaixo.
2
OSG 7861/07
Aula 06
Com base no exposto, atenda às solicitações abaixo.
a) Na figura inserida no espaço destinado à resposta, está representada a montagem incompleta de um circuito. Complete tal montagem inserindo corretamente as quatro lâmpadas, de forma que elas fiquem acesas em suas especificações
nominais.
b) Determine a corrente fornecida pela bateria após a montagem do circuito.
As lâmpadas L1 deverão ser associadas em série,
enquanto s lâmpadas L2 associadas em paralelo.
A)
b) Nas lâmpadas L2
Nas lâmpadas L1
A corrente total
5.
→
P2 = V . i2
→
12 = 12i2
→
i2 = 1A
P1 = V1 . i1
→
12 = 6i1
→
i1 = 2A
i = i1 + i2 +i2
→
i = 4A
(UFMA-2007) As figuras abaixo representam, respectivamente, um circuito elétrico e o gráfico das curvas características
dos componentes desse circuito. Utilizando essas informações, determine o valor da corrente elétrica que passa no circuito.
Gerador: ε = 40V
OSG 7861/07
r
N
tg α =
10
→ r = 5Ω
2
3
Aula 06
N
tg α =
Resistor
R
Receptor
ε’ = 10V
40
→ R = 20Ω
2
r’
N
tg α’ =
10
→ r’ = 5Ω
2
∑ε = ∑Ri → 40 – 10 = 20i + 5i + 5i → 30 = 30i → i = 1A
6.
(UERJ-2007) Um circuito elétrico é composto de uma bateria B de 12V que alimenta três resistores –X, Y e Z–, conforme
ilustra a figura abaixo.
Considerando que os resistores têm a mesma resistência R, calcule a ddp entre os terminais do resistor Z.
•
Resistência equivalente
•
Corrente total
•
Tensão no resistor Z
i=
Req =
R
3R
+R=
2
2
U
2U
=
Req
3R
UZ = R x i =
UZ =
2
U
3
2 x 12
= 8V
3
UZ = 8V
7.
(FUVEST-2007) Em uma ilha distante, um equipamento eletrônico de monitoramento ambiental, que opera em 12V e consome 240W, é mantido ligado 20h por dia. A energia é fornecida por um conjunto de N baterias ideais de 12V. Essas baterias são carregadas por um gerador a diesel, G, através de uma resistência R de 0,2Ω. Para evitar interferência no monitoramento, o gerador é ligado durante 4h por dia, no período em que o equipamento permanece desligado. Determine:
C
a) a corrente I, em ampères, que alimenta o equipamento eletrônico C.
b) o número mínimo N, de baterias, necessário para manter o sistema, supondo que as baterias armazenem carga de
50A . h cada uma.
c) a tensão V, em volts, que deve ser fornecida pelo gerador, para carregar as baterias em 4h.
NOTE E ADOTE
(1 ampère x 1 segundo = 1 coulomb)
O parâmetro usado para caracterizar a carga de uma bateria, produto da corrente pelo tempo, é o
ampère . hora (A . h).
4
OSG 7861/07
Aula 06
Suponha que a tensão da bateria permaneça constante até o final de sua carga.
a) A corrente (I) é dada por:
P = U . I ⇒ 240 = 12 . I ⇒
I = 20A
b) O número (N) de baterias necessárias é obtido de:
|Q |
50
⇒ 20 = N .
⇒ N = 8 baterias
I=N.
∆t
20
c) A corrente (i) necessária para recarregar as N baterias em ∆t’ = 4h é dada por:
50
|Q |
i=N.
=8.
= 100Q
4
∆t '
Assim, sendo ε’ = 12V a f.c.e.m. das baterias, aplicando a Lei de Ohm-Pouillet na malha da esquerda, temos:
I = R + ε’ – V = 0 ⇒ 100 . 0,2 + 12 – V = 0 ⇒
8.
V = 32V
(UFU 2007) O circuito abaixo pode ser utilizado como um aquecedor de líquidos. Isto pode ser feito variando a resistência
R do circuito.
Sendo a diferença de potencial utilizada no circuito de 100V e as duas resistências r de 2,5Ω, determine:
a) a resistência equivalente do circuito, em função de R.
b) o valor da resistência R para que após 10 segundos a energia total dissipada nos resistores deste circuito seja de 105J.
a) R’ é a resistência equivalente das resistências r = 2,5Ω
R’ = 2r → R’ = 5Ω
Re =
R x R'
→
R + R'
Re =
5R
R+ 5
V2
V2 . t
(100)2 x 10
. t → Re =
=
⇒ Re = 1Ω
Re
U
105
5R
5R
⇒
= 1 → 5R = R + 5 → 4R = 5 → R = 1,25Ω
Re =
R+ 5
R+ 5
b) U = P . t → U =
OSG 7861/07
5
Aula 06
Say281107/Rev.:
6
OSG 7861/07