Folhetim 12 - Galera da Física

ANO II - No 12
FOLHETIM
IM
PR
ES
SO
ABRIL - 2000
O JORNALZINHO DA GALERA DA FÍSICA
Distribuição Gratuita - Folhetim na Internet: www.cen.g12.br/f2g/jornal
CADÊ O PONTO G?
Preocupado com a banda podre
e a aceleração da gravidade do
crime organizado no Rio de Janeiro, o Folhetim testou e aprovou uma engenhoca pega-ladrão, financiada com a sobra de
caixa do superfaturamento das
quentinhas das penitenciárias. A
máquina funciona de forma muito simples: ao perceber a chegada do larápio, você liga um tocadiscos, queima um barbantinho
cheiroso e atira 2 pedras, simultaneamente, no meliante. Marcelo Fonte Boa garante que dá cer-
to, e vai dispensar as duas viralatas legítimas que tem em casa.
Para o físico e ex-cantor do coral da UFF, Luiz Alberto, mais
conhecido como “Gui-gui, a criança louca”, a interpretação desse experimento requer do indivíduo uma leitura e uma dinâmica
sócio-cultural transcendente, já
que a invenção do professor Alexandre está carregada de um
corpus teórico revolucionário,
que permite encontrar o ponto g
em homens, mulheres e simpatizantes afins - Página 11
Corrupção
Paulista perde
trem das onze e
chega ao
sistema solar pega táxi
Estrelasbrilham,
mas não fazem
Plim-Plim
O grande erro de Aristarco, ao tentar construir a rodovia Terra/Sol, foi
não ter aplicado o fator K de recomposição de preços. Com o fator K,
ele teria encontrado uma distância
deferente, superfaturada, 20 vezes
maior do que encontrou. Aristarco
foi sumariamente rejeitado pelos
empreiteiros que faziam parte da
banda podre da época - Página 2
Na segunda parte da entrevista
com Henrique Lins de Barros, diretor do Mast, você vai descobrir
por que a ciência e o gel do cabelo
do Willian Bonner não combinam
muito bem - Página 7
Quanto custa ao contribuinte de
São Paulo perder o trem das onze
e atravessar o túnel Ayrton Senna,
depois de um dia de trabalho?
Aplicando o fator K de recomposição de preços, mais stress, engarrafamento e notas fiscais frias,
o valor obtido pelos empreiteiros
com certeza é um rombo no seu
orçamento - Página 6
Guia santificado e Einstein canonizado
Na coluna “O que há para ler”, a bola da vez é um guia de endereços
celestes, que traz o e-mail de São Jorge e a caixa postal de Santo Expedito, para quem estiver na pior. Aproveitando a carona nesta chamada,
recomendamos também a nova seção “Deu na Internet”, com a matéria
sobre o aluno de São Einstein, que ganhou nota 10 por ter proposto o
uso de um barômetro para medir a pressão da avó - Páginas 16 e 14
Feira de Ciências
O que já era bom, agora está
D+! O professor Léo inaugurou seu site:
www.feiradeciências.com.br.
Sempre com novidades, ficou
imperdível. Dê a dica para seus
alunos. Vale a pena!
FOLHE TIM
2
Prezado
Colega
,
Com este número, estamos criando a seção: “Perguntar não
ofende”. Extra-oficialmente, ela
já foi lançada no Folhetim 11,
com a pergunta proposta pelo
professor Cesar Bastos:
“Um menino me perguntou:
Por que a bola de golfe apresenta depressões em sua extensão?”
As respostas recebidas estarão disponíveis em nosso site (que
está de cara nova a partir deste
número. Não deixe de ver!).
Essa é a idéia da seção: sabe
aquela “perguntinha” que algum
aluno lança, e que a gente não
tem a resposta na hora? Coça a
cabeça, diz que vai pensar um
pouco mais, e sai em busca de
auxílio dos colegas?
Pois é, uma vez lançada a pergunta - e esperamos que todos
colaborem, pois não há professor que não tenha uma boa coleção delas - publicaremos as respostas que forem chegando.
Cada um então analisa, pensa,
concorda ou discorda. Não nos
preocuparemos em destacar a
“resposta correta”. Pois, como
já dizia o Velho Guerreiro, “Eu
não vim para explicar, eu vim
para confundir”. E a seção veio
para isso.
P.S.: Perdemos um redator,
ganhamos um correspondente internacional. O professor Mauro
Santos Ferreira foi convidado
por um grupo de pesquisa da
Technology University of Delft,
e irá passar (pelo menos) 2 anos
por lá, na Holanda, a terra dos
dois ganhadores do Prêmio Nobel 99.
Boa sorte, Maurinho!
ABRIL DE 2000
FOLHETIM CONFIRMA CRENÇA POPULAR
SÃO JORGE
MORA NA LUA
epiciclo
DISTÂNCIAS
NO SISTEMA SOLAR
Em artigo anterior (veja Folhetim número 11), mencionamos o
grande erro de Aristarco ao tentar
medir a distância Terra/Sol e encontrar que ela vale apenas 20 vezes mais do que a distância Terra/
Lua (o que, certamente, não desmerece todas as outras medidas
que obteve com enorme precisão).
A primeira determinação razoável dessa distância só veio a acontecer muitos séculos depois. Ela
precisou esperar a mudança de modelo do sistema solar, do geocêntrico de Ptolomeu para o heliocêntrico de Copérnico (que viveu de
1473 a 1543. Já estamos, portanto, em meados do século XVI).
Curiosamente, Aristarco já havia
proposto este modelo, que foi sumariamente rejeitado pelos astrônomos de sua época!
Inúmeras obras de altíssima qualidade tratam de modo mais ou menos profundo as questões envolvidas
nessa mudança de referencial, e nas
diferenças entre os dois modelos.
Para o que nos interessa neste artigo
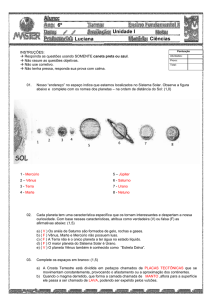
- a determinação da distância Terra/Sol -, a figura 1 (adaptada do livro do Prof. Nussenzveig) é suficiente. Em (a), temos as posições e
os movimentos relativos do Sol, da
Terra e de Vênus, no modelo Ptolomaico: a Terra imóvel, o Sol girando em torno dela, numa órbita
denominada deferente, e Vênus
descrevendo em torno do Sol o que
Ptolomeu chamava de epiciclo.
V ênus
S ol
deferente
Terra
(a)
V ênus
S ol
(b)
Terra
fig u ra 1
Em (b), a descrição de Copérnico: Terra e Vênus girando em torno do Sol, do mesmo modo que
giram os outros planetas: Mercúrio, que assim como Vênus, descreve uma órbita de raio menor que
o da Terra, e por isso são denominados planetas interiores; Marte,
Júpiter e Saturno, os planetas exteriores, pois descrevem em torno do
Sol órbitas externas à da Terra.
Urano, Netuno e Plutão não podem
ser vistos a olho nu, e não eram conhecidos na época de Copérnico (a
descoberta desses três planetas foi
um grande triunfo da teoria da gravitação de Newton, bem como do
desenvolvimento da tecnologia de
FOLHE TIM
ABRIL DE 2000
observação astronômica. Certamente será contada no próximo artigo).
O modelo de Copérnico provocou, entre outras coisas, uma mudança de enfoque no problema da
determinação das distâncias celestes. Ele não mais trazia a preocupação de medir as distâncias dos
planetas até a Terra (centro do sistema ptolomaico), mas sim deles
até o Sol. E Copérnico fez essas
medidas de modo extremamente
engenhoso, como veremos a seguir.
A escala relativa
Antes de medir a distância Ter-
PLANETA
Mercúrio
Vênus
Terra
Marte
Júpiter
Saturno
ra/Sol, Copérnico estabeleceu a
escala relativa das distâncias de
todos os planetas ao Sol. Explicando melhor: utilizando como unidade a distância Terra/Sol, que
doravante denominaremos RT (atualmente ela é chamada unidade astronômica, ou seja, RT = 1 U.A.), ele
conseguiu medir os raios das órbitas
dos outros planetas em torno do Sol.
Para se ter uma idéia da precisão de
suas medidas, apresentamos na tabela uma comparação com os valores atualmente aceitos.
Vejamos, por exemplo, como ele
COPÉRNICO
(U.A.)
0,376
0,719
1,000
1,520
5,219
9,174
determinou o raio (RV) da órbita de
Vênus. A figura 2 mostra a posição relativa dos três astros no dia
em que, visto da Terra, o afastamento angular (qMAX) entre Vênus
e o Sol é máximo (lembramos que,
como as velocidades orbitais são
diferentes - quanto mais perto do
Sol o planeta, maior a sua velocidade -, este ângulo muda no decorrer do tempo. Convença-se disso, imaginando outras posições relativas para Vênus em sua órbita).
ATUAL
(U.A.)
0,387
0,723
1,000
1,524
5,203
9,539
Tomando como base dados
coletados por vários astrônomos
que o antecederam, que forneciam
para qMAX um valor próximo de 46o
(ver nota 1), Copérnico pôde determinar RV em função de RT (ou
seja, na tal unidade astronômica).
A figura 2 anterior nos mostra que,
no afastamento máximo, o ângulo
no vértice de Vênus vale 90o, de
modo que:
sen θ MAX =
RV
90
θM A X
o
Vênus
Terra
fig ura 2
A distância Terra/Sol
Tudo bem. Já sabemos as distâncias dos planetas ao Sol, tendo como
unidade o raio da órbita da Terra (RT).
Mas quanto vale RT, cuja determinação é o objetivo central deste artigo?
Kepler (1571-1630) foi o primeiro a medi-la, através de um processo indireto. Utilizando o método da
paralaxe (ver nota 3), ele determinou inicialmente a distância entre
Terra e Marte, e daí obteve RT. No
século seguinte (isso já em 1761),
obteve-se uma medida de maior precisão, com base em uma sugestão
proposta por Halley: mediu-se a distância (d) entre Terra e Vênus, quando este está passando bem em frente ao Sol. Novamente, o método utilizado foi o da paralaxe, observando-se Vênus no mesmo momento a
partir de dois pontos distintos da superfície da Terra. A figura 3 mostra a
situação:
d = RT - RV
RV
Vênus
d RT
Terra
figura 3
O valor encontrado foi
RV
RT
⇒ R V = R T ⋅ sen 46
RT
3
d @ 4,2 x 107 km.
o
Portanto, RV = 0,719 U.A., tal
como obtido por Copérnico.
Utilizando procedimentos semelhantes, ele obteve a relação entre
os raios das órbitas dos outros planetas e o da Terra (a coisa complica um pouco quando se trata dos
planetas exteriores. A esse respeito, veja nota 2).
Utilizando a relação entre os raios das
órbitas de Vênus e da Terra, obtida
por Copérnico, teremos:
RV = 0,72RT
mas d = RT - RV, de modo que:
4,2 x 107 km = 0,28 RT
RT = 1,5 x 108 km
ou seja, cerca de 150 milhões de
quilômetros!!!
FOLHE TIM
4
Conclusões
Assim que se determinou a distância Terra/Sol, chegou-se a uma série de outras medidas importantes.
Vejamos algumas:
- A obtenção dos valores absolutos, e não apenas relativos, dos
raios das órbitas dos demais planetas. Por exemplo: a distância de
Marte ao Sol vale:
RM = 1,52 RT = 2,3 x 108 km
- A determinação do tamanho do
Sol. Como já havíamos visto, a Lua
está a 380 mil quilômetros da Terra,
e o Sol, a 150 milhões de km. Fazendo as contas, encontramos que o
Sol está cerca de 400 vezes mais longe que a Lua (e não a apenas 20,
como mediu Aristarco!). Ora, como
possuem o mesmo tamanho aparente, o Sol deve ser 400 vezes maior
do que a Lua, ou seja:
RSOL = 4 x 102 RLUA =
= 4 x 102 x 1,7 x 103 = 6,8 x 105 km
(o valor atualmente aceito é
6,96 x 105 km)
- A determinação da massa do Sol.
Aplicando convenientemente a lei
da gravitação de Newton (estabelecida em 1697), juntamente com
a sua segunda lei, para um satélite
em órbita circular de raio R e período T, em torno de um astro de
massa M, obtemos a relação:
R3
T
2
=
Bibliografia básica
Nussenzveig, M., Curso de Física Básica - Mecânica, Editora Edgard Blücher
Ltda, SP (1981).
Lucie, P., Física Básica, Fundação
Cesgranrio, RJ (1975).
Notas
1. O afastamento angular máximo de
Vênus em relação ao Sol, visto da
Terra, traz duas conseqüências. A
primeira: Vênus nunca será visto no
céu noturno bem “em cima” de nossa cabeça: ele sempre estará a menos de 46o com a linha do horizonte,
num ângulo que diminui à medida que
anoitece. E mais: como a Terra gira
em torno de seu próprio eixo com uma
velocidade angular constante e igual
a 360o/24h = 15graus/hora, se alguém
lhe disser que viu Vênus brilhando no
céu, digamos, às 11 da noite, certamente estará confundindo Vênus com
alguma estrela brilhante. Raciocinemos juntos: mesmo quando está no
seu afastamento angular máximo do
Sol, Vênus permanece acima da linha do horizonte apenas 3 horas após
o Sol se pôr (resultado da divisão de
46o por 15o/h).
2. Para os planetas exteriores, Copérnico teve um pouco mais de trabalho. Exemplifiquemos com Marte.
A figura 4 mostra as posições relativas dos três astros, Sol, Terra e Marte equivalentes àquelas usadas para
determinar o raio da órbita de Vênus:
Observe que, da Terra, não po-
G⋅M
4 ⋅ π2
Assim que a constante de gravitação universal G foi determinada
por Cavendish em 1798, e com o
conhecimento do raio da órbita da
Terra em torno do Sol (o período
já era conhecido há séculos, e vale
365 dias), pôde-se determinar a
massa do astro em torno do qual a
Terra orbita, ou seja, o Sol. Faça
as contas e encontrará:
MSOL @ 2 x 1030 kg
RM
RT
90
θM A X
o
Terra
M arte
fig u ra 4
demos medir o ângulo qMAX, que nos
permitiria escrever que:
R
sen θ MAX = T
RM
ABRIL DE 2000
⇒ R T = R M ⋅ sen θ MAX
A solução que Copérnico deu ao
problema envolve o conhecimento dos
períodos das órbitas dos planetas em
torno do Sol (denominados períodos
siderais). Acontece que, na época, o
que se conhecia eram os períodos
sinódicos, ou seja, o tempo que os planetas levavam para dar uma volta
completa em relação à Terra (pois o
modelo aceito era o geocêntrico). No
próximo artigo, aprofundaremos a diferença que existe entre os períodos
sinódicos e siderais, mostrando de que
modo estes foram determinados por
Copérnico.
3. Este método foi (e ainda é) muito
utilizado para medir distâncias astronômicas, desde que não muito
grandes (da ordem de 10 anos-luz,
no máximo). A figura 5 esclarece o
procedimento:
Imagine que desejamos medir a
distância d, de um objeto distante O
até a superfície que passa por AB
O
θθ
d
B
A
figu ra 5
(por exemplo, de Vênus até a superfície da Terra). Conhecendo a
distância AB, basta medir o ângulo
2q entre as duas visadas, obtendo,
para d, o valor:
AB
AB
⇒ d=
2⋅d
2 ⋅ tg θ
(q é chamado de ângulo de paralaxe)
O problema prático é que, quanto mais longe o ponto O, menor o
ângulo q e maior o erro relativo em
sua medição (já imaginou medir ângulos de frações de grau?). Por isso
este método não dá bons resultados
quando o objeto (por exemplo, uma
estrela) está muito distante.
Luiz Alberto Guimarães
[email protected]
tg θ =
ABRIL DE 2000
Onde
está o
Mauro?
PARTE 1
FOLHE TIM
5
AFINAL
URO FOI F
AZER NA HOLAND
A?
AFINAL,, O QUE O MA
MAURO
FAZER
HOLANDA?
Existem umas técnicas que nós,
Físicos, usamos que são muito úteis
para descrever o transporte de corrente elétrica através dos materiais.
Minha função na Holanda vai ser
aplicar essas técnicas numa área
completamente diferente da minha,
que é a sismologia. Eles estão interessados em ver como uma onda so-
nora se propaga no interior da Terra.
Então, ao invés de falar em transporte
de corrente elétrica, vou estudar o transporte de ondas acústicas. Muda um
pouco, mas no fundo é tudo muito parecido. O elétron é tratado como uma
onda em mecânica quântica e, portanto, a linguagem é quase a mesma.
Mauro Santos Ferreira
FOLHE TIM
6
ABRIL DE 2000
DEU NA REVISTA
Vou de táxi?
Aplique seus
conhecimentos
Para responder as perguntas seguintes, considere que os valores da tabela da QUATRO RODAS
sejam as velocidades médias em todos os deslocamentos propostos.
1. Um morador de São
Paulo sai cansado do trabalho, no final da tarde, e
gasta 40 minutos de carro para chegar em casa. Qual a distância (em
km) que ele percorre?
2. Um estudante do Recife mora a
16km de sua escola. Com quanto
tempo de antecedência ele deve sair
de casa, pela manhã, para não chegar
atrasado? Dê a resposta em minutos.
3. Um morador de Belo Horizonte gasta 30 minutos para ir ao trabalho. Quanto tempo a menos gasta um morador de Juiz de Fora, que
faz o mesmo deslocamento?
4. A figura (adaptada do Guia QUATRO RODAS) apresenta um trecho
da cidade do Rio de Janeiro, entre
as praias de Ipanema e Copacabana.
Considere um automóvel que se desloca pela Av. Vieira Souto (a partir
do encontro dela com a Av. Rainha
Elisabete), entra na Rua Francisco
Otaviano e pega a Av. Nossa S. de
Copacabana, indo até o cruzamento
com a rua Sá Ferreira. Para facilitar
os cálculos, considere que, neste
mapa, 1cm representa 200m. De-
termine o deslocamento
escalar e o módulo do deslocamento vetorial efetuado pelo automóvel.
5. Qual dos deslocamentos (escalar ou vetorial)
obtidos na questão 4 você
utilizaria para:
a) Calcular o tempo gasto
no trecho? Calcule este
tempo, utilizando a velocidade fornecida na tabela.
b) Estimar o consumo de combustível?
c) Calcular o tempo que um helicóptero gastaria para se deslocar
em linha reta entre as posições inicial e final do automóvel?
d) Estimar o tempo que uma explosão ocorrida no ponto de partida levaria para ser escutada no
ponto de chegada?
6. Considerando o tempo obtido
em (5.a), qual o módulo da velocidade vetorial média do carro (em
km/h) durante seu deslocamento?
O que este valor representa?
Respostas
1. aproximadamente 11km
2. 40 minutos
3. 8 minutos a menos
4. 2,6 x 103 m e 1,6 x 103 m,
respectivamente.
5. a) O escalar; 6 minutos.
b) O escalar
c) O vetorial
d) O vetorial
6. Cerca de 16km/h. Poderia representar, por exemplo, a velocidade de
um helicóptero que, deslocando-se
em linha reta, partisse do mesmo
ponto e no mesmo instante que o
automóvel e chegasse junto com ele
ao final do percurso.
Luiz Alberto Guimarães
[email protected]
ABRIL DE 2000
ENTRE
VISTA
Fique antenado na segunda parte da entrevista com
Henrique Lins de Barros, diretor do Museu de Astronomia e Ciências Afins. Além
das informações relativas aos
programas do museu, Henrique faz uma série de questionamentos. Um deles é sobre
a ausência de conteúdo quando a ciência vira notícia nos
meios de comunicação. Nesta entrevista, ele também
fala sobre a função do cientista na sociedade moderna, a quem é atribuído
o papel de mago, “capaz
de resolver qualquer problema” e sobre a visão estereotipada que se tem dos
astrônomos e pesquisadores científicos, tidos como
lunáticos.
Folhetim: Como funciona o programa de exposições do Mast?
Henrique: A tendência é que toda
exposição termine por permanente. Há no museu exposições que
ficam um tempo, saem, e retornam.
Não teria sentido a gente investir
dinheiro para a construção de uma
exposição e depois desmontá-la.
Nós temos uma exposição permanente, na verdade um projeto
museológico, chamada Quatro
Cantos de Origem que é a cara do
museu. É uma referência às quatro
teorias importantes do século XX.
Em cima da origem do universo, da
matéria, da vida, da informação,
construímos várias leituras. O projeto determina, inclusive, a política
FOLHE TIM
de aquisição e descarte. Um museu
não é um local onde você deposita
tudo. Temos cerca de 2.000 instrumentos, a maior parte do século
XIX, expostos à visitação pública.
Trabalhar com 2.000 instrumentos necessita tempo e recursos.
Uma solução foi fazer uma introdução à exposição mostrando que o
homem, ao desenvolver a ciência
moderna, teve a necessidade de um
instrumento de medida. Assim, ele introduz a noção de precisão na medida e a precisão é um instrumento.
Há também um contraponto entre o céu medieval e o céu científi-
co do século XX. Falamos um
pouco da teoria geocêntrica, das
idéias ptolomaicas. Depois, é a vez
das navegações, da expansão do
mundo europeu, levando à necessidade da reformulação das idéias
ptolomaicas/aristotélicas. Surge a
idéia de leis universais, com validade não só na Terra, mas validade geral. Quando a Terra perde a
posição de singularidade ela passa
a ser um ponto no universo. Então,
o que vale na Terra, vale fora.
Chegamos a Newton e idéias
mais recentes. Você vai olhar o céu
não mais no seu valor simbólico,
onde as constelações zodiacais
determinam práticas e personalidades, mas o céu do século XX ou
de coordenadas. Essa exposição
7
introdutória leva à reserva técnica,
ao acervo. Na proposta da ciência
moderna, um instrumento é importante. Não é uma coisa surgida do
acaso, mas dentro de um corpo de
conhecimentos.
Buscamos criar um certo envolvimento da pessoa com a questão científica, muitas vezes considerada árida. Tentamos envolver o
indivíduo no seu cotidiano, nas suas
práticas e curiosidades. Num dos
nossos laboratórios (sobre ciclos
astronômicos) colocamos uma colméia e um aquário.
Como a colméia se comporta
num dia frio, num dia quente ou à
noite? Como os organismos dentro do aquário de maré mudam
características comportamentais,
ambientais? A maré está ligada
ao movimento da Lua, à rotação da Terra .A compreensão
do mundo não é só para o deleite próprio, mas para se tentar entender o mundo natural.
F: No que consiste o “Brincando com a ciência” e o
“Oficina de ciências?
H: O “Oficina de Ciências” é
um programa para treinamento de
professores onde ensinamos a
construir módulos experimentais com
material muito simples. Com a sucata disponível do tipo papel, grampo,
embalagens, você constrói um experimento para demonstrar um fenômeno. Se você tiver leitura suficiente,
serve para evidenciar um conceito.
Um experimento não é uma coisa que acontece por acaso. O experimento é construído com intenção. Quando eu quero ver, por
exemplo, o movimento retilíneo
uniforme, não basta jogar um carrinho porque ele pára do outro
lado. Para ver o movimento vou
construir o carrinho num plano um
pouco inclinado para compensar o
atrito; vou colocar uma rodinha es-
8
pecial para evitar a dissipação de
energia etc. Esse aprendizado a gente passa para o professor. O que o
museu fez em 10 anos de experiência, foi propor a construção de experimentos simples, duráveis e eficientes para usar em sala de aula.
O “Brincando com a ciência” é
um programa de atendimento ao
público e foi a semente de vários
outros programas do museu. Nossa equipe constrói aparatos feitos
com sucata para a demonstração
de fenômenos e o público brinca
com eles. No “Brincando com a
ciência” o museu está aberto ao
público em geral. Ele acontece nas
tardes de domingo.
F: Vocês também têm duas publicações: o “Brincando com a
ciência” e o “Caderno do Professor”. Qual o conteúdo delas?
H: O programa “Brincando com a
ciência” tem como filhote um caderno com o mesmo nome. É um
caderno grande, onde as experiências são explicadas para serem
montadas. É uma publicação do
museu e pode ser adquirida. A outra publicação serve de suporte
para os professores nas visitas orientadas. No “Caderno do Professor” traduzimos, segundo uma ótica, essas conversas que estamos
tendo sobre o museu. Existem textos sobre o projeto museológico,
astronomia e os espaços do museu, fornecendo ao professor um
material a ser utilizado posteriormente em aula.
Aproveito para falar no Parque da
Ciência, um projeto piloto do museu
construído em Vitória. São brinquedos de parque de diversão criados
com uma intencionalidade. Você não
faz simplesmente um balanço. Faz um
balanço em 3 comprimentos diferentes, ou seja, você faz pêndulos. E, aí,
você coloca um letreiro e diz: o balanço de menor comprimento oscila
FOLHE TIM
diferente da freqüência do balanço
de maior comprimento, dando conta desses conceitos.
F: Gostaria que você abordasse sobre as relações entre educação formal e não formal.
H: O museu de astronomia é um
laboratório de pesquisa. Seu produto está à disposição da sociedade para a construção de uma reflexão. Evidentemente, a dinâmica
de uma visita é uma dinâmica não
formal. Com uma turma você pode
dirigir um pouco a visita. Com o
público avulso não. Ele entra se
quiser, se não quiser, fica no pátio.
O museu como espaço não formal passa uma informação e você
tem uma coisa interessante: o olhar
aqui é diferente do olhar da escola. O público vem com a liberdade
de vir, não tem cobrança de horário nem cobrança de avaliação.
Como o público assimila as informações do museu? Será que
assimila alguma coisa? Nossa linguagem tem eficiência para o público avulso e o escolar? Tais
questionamentos levam-nos a um
estudo mais aprofundado do que
se chamaria educação não formal,
em contraposição a um espaço escolar, de educação formal. Temos
um trabalho de pesquisa ainda em
desenvolvimento buscando identificar essas diferenças.
Pessoalmente, considero importante você olhar com mais carinho
a relação familiar e de como a ciência é lida nesse espaço também
não formal. A família é cada vez
mais bombardeada pela informação. O Jornal Nacional é visto no
Brasil inteiro e sempre tem um segmento dedicado à ciência. Eles informam que os cientistas descobriram uma barbaridade qualquer ou
provaram outra barbaridade qualquer. O compromisso do Jornal
Nacional é zero com o conteúdo.
ABRIL DE 2000
A informação é instantânea, jogada
para despertar interesse. Que efeito
ela vai produzir na família? Como a
educação não formal, através dos
meios de comunicação, repercute?
Ela tem ou não eficiência?
O momento é de forte impacto
tecnológico, exigindo do indivíduo,
do profissional maduro, uma
reciclagem. Se ele não tem tempo
de voltar à escola, como vai ser
informado sobre ciência? Que ciência é essa que ele está processando via espaços não formais
como tv, vídeos, jornais, internet?
A ciência por ele assimilada é aquela que nós cientistas gostaríamos
que ele soubesse? Ou será que a
ciência está sendo transformada
numa grande religião científica sem
compromisso com a coerência ou
conceitos fundamentais? Tal situação dá uma tranqüilidade para o
indivíduo dizer: o problema não é
meu, porque o cientista resolve.
F: Como fica o cientista nisso
tudo?
H: Eu vejo, por exemplo, muita
gente dizer sobre a destruição ecológica do mundo, que o problema
é sério e os cientistas vão ter muito
trabalho. Na verdade, é um problema sério e os cientistas não estão conseguindo resolver. A questão exige um reposicionamento da
sociedade diante de um conceito
completamente fora das ciências
exatas: a noção de progresso. Se
modelamos o progresso na idéia de
transformações contínuas para
bens materiais, talvez o problema
ecológico seja insolúvel.
Vemos notícias de que o Projeto Genoma está decodificando o
gene humano para uma seleção técnica ou tecnológica do indivíduo,
indo muito além daquilo que a ciência se propôs um dia e muito além
da responsabilidade do cientista. É
a mesma coisa com os trangênicos.
A intervenção no processo de evolução natural terá implicações futuras e poderá nos comprometer? Ou
será a intervenção somente positiva?
Os espaços da educação não
formal têm que ser olhados com
uma preocupação maior do que há
20 anos. Quando se entendia que
a educação ocorria do período escolar à graduação. Hoje a informação passou a ser um elemento importante para a pessoa se considerar um cidadão, ou seja, um indivíduo inserido num contexto cultural capaz de, até certo ponto, de
ter uma opinião. A grande dúvida
é a forma de se encarar a ciência.
O cientista é o grande mago da sociedade moderna, capaz de resolver qualquer problema. A gente
deposita nele toda a responsabilidade e vamos vivendo, tirando os
lucros materiais, sem uma perspectiva de longa duração. No fundo a
gente poderia dizer que há um conflito, ou uma tensão, entre a lógica
do indivíduo - o que é melhor para
ele - e a lógica de uma espécie. A
lógica do indivíduo pode estar em
oposição à lógica do grupo.
Hoje você vive mais uma lógica
individual, na solução do seu problema, embora o seu discurso seja
carregado de uma hipocrisia de
estar sempre falando de democratização do mundo. Talvez não exista democratização possível.
F: Fala-se pouco, ou quase nada,
dos astrônomos no Brasil.
H: Nós não ouvimos falar nos astrônomos brasileiros, mas ouvimos
falar dos astrônomos americanos.
A gente ouve falar do Hubble a
cada minuto...
F: Ouve-se falar muito do fato
(do telescópio Hubble), mas a
sensação é que o criador, o cientista, está em segundo plano...
H: Sua visão está muito na direção daquilo que chamo de idade
FOLHE TIM
tecnológica, ou seja, o aparato
tecnológico domina a criação humana. Então, quando você ouve
uma notícia sobre o Hubble, o impressionante é o Hubble, e não
quem foi capaz de construí-lo,
entendê-lo. Quando você ouve falar sobre o Projeto Genoma, raramente vai ouvir a respeito de quem
está decodificando. É o biólogo, o
físico, o geneticista... quem? Então,
a questão da profissionalização de
uma área se dilui porque o fato
tecnológico domina. O grande milagre é tecnológico e não do indivíduo. O grande milagre na verdade é a nossa criação humana, nossa capacidade de pensar.
Eu diria que a visão sobre o astrônomo é um estereótipo, assim
como a visão sobre o cientista. Eu
não sou astrônomo, há mais de 10
anos trabalho em biofísica. A gente pensa no cientista como uma
pessoa deslocada do mundo material. Ela é distraída, tem pensamentos que ninguém entende, está
no mundo da Lua. O mundo da
Lua, como o próprio termo fala, é
o mundo do astrônomo.
Existe uma construção romântica, no século XIX, sobre o pesquisador, não compatível com a
realidade. Nenhum pesquisador
está deslocado do seu mundo. A
imagem de Einstein mais conhecida é ele descabelado, com a língua
para fora. No entanto, a ação política dele, nas décadas de 20 e 30,
até a sua morte, em prol do povo
judeu, foi importante e relevante.
Em 1925, quando Einstein passou
pelo Brasil, ele estava indo para a
Argentina discutir a questão judaica. Isso não é uma visão de uma
pessoa deslocada do mundo. Em
1925 ele já se preocupava com o
que iria acontecer. O trabalho do
cientista não elimina a sua preocupação com a sociedade.
9
“
Eu costumo dizer que,
se parássemos para lembrar e refletir sobre tudo que
nos fizeram na escola e não
fizéssemos o mesmo, agora,
como professores, já estaríamos revolucionando a escola... Meu primeiro motor
de transformação não foi o
que descobri nas pesquisas,
mas esta pergunta: o que
me incomodava na escola?...
O que mais me incomodava na escola quando jovem era a falta de sentido
das coisas que aprendíamos. A pergunta que mais
se formula ainda hoje é
para que serve isto? E a resposta que se tem sempre é
que se precisa saber para
o ano seguinte, para o outro curso, para a prova,
para o diploma, numa rotina de cerimônias que dependem umas das outras
para que possamos ir em
frente, mas que nada têm a
ver com nossas vidas. Escola e vida não estão interligadas.
Jurjo Torres Santomé
“
ABRIL DE 2000
ao
a-
FOLHE TIM
10
s
@
t
r
c@
Neste número, estamos dedicando este espaço à divulgação
de uma excelente notícia para
todos os Professores de Física
no Ensino Médio. Acreditamos
que, em breve, todos poderemos contar com mais um veículo dedicado à melhoria da qualidade do ensino de Física.
Caro(a) Colega,
O Conselho Editorial da RBEF
constatou que a revista tem dificuldades em despertar o interesse dos professores de Física dos
Ensinos Fundamental e Médio e
das escolas brasileiras.
Na tentativa de contribuir para
a melhoria do Ensino de Física
nestes níveis, estamos lançando
a revista “A Física na Escola”,
um suplemento da RBEF dirigida
ao professor do Ensino Médio.
Apresentamos aqui uma proposta para as Seções do Suplemento:
- Artigos Convidados
Divulgação de tópicos atuais de
conteúdo e metodológicos de interesse para o ensino médio
numa linguagem acessível.
- Desafios
Problemas desafiadores de Física, que têm sido propostos em
diversas situações, como Livros,
Gincanas, Olimpíadas, etc. com
solução discutida em detalhes.
Tais problemas constituem subsídios aos professores que lidam
com alunos com grande interesse e motivação pelos limites da
Física.
- Faça você mesmo
Divulgação de experimentos e
demonstrações simples que qual-
quer estudante pode realizar sem
dificuldades. A idéia é propiciar
material de fácil acesso a professores do ensino fundamental e
médio.
- Relatos de Sala de Aula
Divulgação de experiências valorizando as vivências de salas
de aula.
- História da Física e Ensino
Explorar certos conceitos e/ou
experiências que ilustrem a evolução dos conceitos da Física.
Fonte de inspiração para a definição de conteúdos e proposição
de estratégias.
- Novas Tecnologias no Ensino
de Física
Softwares, vídeos e sites que possibilitem aos professores e/ou alunos utilizarem um computador
como instrumento de ensino/
aprendizagem.
- Avanços da Física
Divulgação no estilo do “Physics
News” da AIP.
- Resenhas
Comentários e informações curtas sobre livros didáticos e paradidáticos e outros.
- Física, Tecnologia e Sociedade
Discussão dos aspectos da interface Física/Sociedade ressaltando as imbricações da ciência
com questões tecnológicas e sociais e de sua necessidade para
uma educação com cidadania.
Resenhas específicas da bibliografia pertinente.
Gostaríamos de abrir um canal
aos interessados no Ensino de Física acerca deste Suplemento e
receber sugestões sobre o conteúdo e formato das seções.
Atenciosamente
Nelson Studart
Editor da RBEF
[email protected]
***
ABRIL DE 2000
Caros Editores do Folhetim,
Gostaria de ser considerado
para a posição de Correspondente Internacional do Folhetim. Soube que um dos seus colaboradores se ausentou e portanto ficou uma vaga disponivel por aí.
Falando sério agora, cheguei e
estou me ajeitando por aqui.
Dêem um alô daí.
Abraços,
Mauro
[email protected]
Prezado Mauro,
Somos contra o nepotismo, mas
com você não vai ter jeito. Mais
do que nosso amigo, colega e
colaborador, você é um irmão
da gente. Considere-se aceito
como o primeiro Correspondente Internacional do Folhetim.
Você não perdeu o emprego, apenas foi transferido. Seu artigo
inaugural poderia ser “A Física e
as Holandesas”. Cuidado com o
excesso de chocolate, cerveja e
com o uso de tamancos.
Um grande abraço,
Toda a equipe do Folhetim
Seja assinante do
FOLHETIM
Para receber GRÁTIS o Folhetim, envie este cupom preenchido para a Rua Macaé, 12,
Pé Pequeno, Santa Rosa,
Niterói/RJ, Cep: 24240-080
Professor:
Endereço completo:
Escola em que trabalha:
Se preferir, passe um e-mail
com todos esses dados para
[email protected]
FOLHE TIM
ABRIL DE 2000
O Método do Toca-Discos, do
Barbante e das Duas Pedras
Pegue um desses toca-discos velhos, de 33rpm. Coloque sobre o
seu prato uma folha de papel branco e cubra-a com uma folha de
papel carbono com a tinta voltada
para baixo. Tome um barbante com
duas pedrinhas atadas nas suas
extremidades e suspenda-o, da forma como mostra a figura 1, deixando uma das pedras quase tocando o disco e a outra a uma certa altura DS. Note que o barbante
passa, por exemplo, sobre uma
prancha de madeira (que pode ser
apoiada nas duas extremidades em
outros objetos). Como você poderá compreender adiante, as pedras devem estar colocadas de tal
forma que suas projeções sobre o
prato estejam alinhadas com o centro deste.
p ranc ha d e
m ad eira
eix o d o prato
∆S
p rato
te num Dt = 0; a mais alta, num Dt
equivalente ao seu tempo de queda. Ligando os dois pontos marcados pelas pedras no carbono ao centro do disco, teremos a determinação de um ângulo (a na figura 2).
α
fig u ra 2
Esse ângulo corresponde ao giro
do disco no intervalo entre as quedas das duas pedras. Uma simples
regra de três nos fornecerá o valor
do tempo correspondente ao giro
do disco naquele ângulo. Sabemos
o tempo que o disco leva para girar 360o e logo podemos conhecer o tempo correspondente àquele
ângulo. Lembrando que D S é a
distância correspondente ao tempo Dt, podemos, uma vez mais,
como no nosso exemplo anterior,
escrever que
DS = VODt + gDt2/2
fig u ra 1
Deste modo, pode-se medir,
com razoável precisão, o valor de
Ponha o prato a girar, ligando o
toca discos.
Queime o
EXPERIMENTE
barbante e as
pedras
cairão
simultaneamente.
VOCÊ V
AI GOST
AR
VAI
GOSTAR
Devido à diferença das alturas DS elas atingirão o
prato em diferentes instantes de
g. O experimento contém, certatempo - a mais baixa, praticamen- mente, vários pressupostos, como
11
todo experimento na Física, que interferem decisivamente na interpretação e na precisão das medidas.
Analise com atenção e tente identificar esses pontos cruciais, discutindo-os com os seus alunos.
O Método do Pêndulo Físico
Este método é conhecido também como o “método do impacto
g”. Ele consiste na utilização de um
pêndulo físico, como uma barra de
madeira, posta a oscilar em ângulos não muito grandes. Observe a
figura 3. Uma barra de madeira é
suspensa, através de um furo em
uma de suas extremidades, por um
prego. Um rolamento seria melhor
que o prego, mas este último quebra o nosso galho razoavelmente.
Por que?
suporte para o pêndulo
prego
barra de m ade ira
(nosso pêndulo)
oscilação
fig u ra 3
Pois bem, ponha o pêndulo a
oscilar e meça o tempo de, digamos, umas vinte oscilações. Divida esse tempo por vinte e terá o
tempo médio de uma única oscilação. Tome esse tempo como sendo o período. Aqui você poderá estar pensando: que forma esquisita de escrever tem
esse cara. Por que
não dizer simplesmente que
esse tempo é
o período,
em vez de
complicar dizendo: “tome
esse tempo como
sendo o período”. Aí, no
entanto, não está, apenas uma
questão de estilo literário, como
pode parecer à primeira vista. A
O VALOR DE G
FOLHE TIM
12
questão é que, como já alertamos
acima, toda interpretação de qualquer experimento está carregada
de um certo pressuposto teórico.
No nosso caso, por exemplo, afirmar que tomaremos esse tempo
médio como sendo o período, implica em assumirmos, tacitamente,
que o tempo das oscilações não
esteja sendo reduzido. Isso, rigorosamente falando, não é verdadeiro, pois devido a vários fatores, que
serão propositalmente desconsiderados, o nosso pêndulo chega mesmo ao repouso. Sua oscilação,
portanto, está longe do caso ideal,
no qual o pêndulo oscila indefinidamente, sem perda de energia. Daí
a importância de minimizarmos o
atrito na suspensão da nossa barra
de madeira. Mesmo assim, tomaremos o nosso pêndulo rudimentar
como se fosse ideal e vocês poderão ficar espantados com a precisão final dos resultados, se tentarem, mesmo, fazer o experimento.
Uma vez conhecido o “período”
do nosso pêndulo, passemos à fase
seguinte. Suspenda a extremidade
livre da barra com um barbante atado na mesma. Passe o barbante
sobre dois pregos, conforme a figura 4. Tome a extremidade livre
dele e amarre-a a uma bola pesada. Mas veja lá, é importante que
seja uma bola, que tenha um formato o mais precisamente esférico. Nada de pendurar um cilindro,
por exemplo. Você perceberá, rapidamente, porque. Coloque uma
folha de carbono cobrindo a face
da barra de madeira voltada para
a bola pendurada, com a tinta voltada para a barra. Marque, na barra, a altura que a bola está suspensa
equilibrando o sistema. Agora,
queime o fio.
O que acontece? A barra cai e
p reg o s
su p o rte
b arb an te
figu ra 4
m a rca s d o
ca rb on o
num percurso equivalente a um
quarto de uma oscilação completa
(ida e vinda) ela dá uma pancada
na bola que estava caindo, deixando marcado um segundo ponto
sobre o carbono. Pronto! Não nos
interessa para onde foi lançada a
bola. O nosso problema não é, no
momento, o estudo de projéteis. O
que nos interessa é apenas a distância, na barra, entre as duas marcas do carbono. Ela equivale à
distância que a bola caiu livremente enquanto a barra oscilava em um
quarto do seu período. Esse tempo, um quarto do período da nossa barra, será o Dt da nossa conhecida equação. O DS é exatamente a distância entre as marcações do carbono na barra. Aplique esses valores encontrados na
equação:
DS = VODt + gDt2/2
Agora você terá condições de
calcular, mais uma vez, facilmente,
o valor de g. Aprecie o valor obtido, dá algo muito bom mesmo. Ele
não dá, no entanto, exatamente, o
valor do livro. Não dá, por exemplo 9,81m/s2.
Quanto você obteve? Você está
fazendo mesmo o experimento? O
que significa esta discrepância entre o valor encontrado e o do livro? Será que o experimento está
errado? Para começar, faça, realmente o experimento. Observe,
também, que 9,81 é um valor médio, que a aceleração da gravida-
ABRIL DE 2000
de varia com local da Terra no qual
seja medida. Por que?
Agora pense no grande número
de simplificações contidas na formulação do nosso experimento
proposto. Pense na questão do
ângulo ter sido sugerido como não
muito grande. Pense no atrito no
prego ou entre o cordão e os pregos. Pense na razão de termos sugerido a utilização de uma bola e
não de um cilindro. Há um mundo
de coisas que podem ser consideradas, pense nelas. Elas são o próprio espírito da concepção do experimento, da construção do nosso conhecimento, da atribuição dos
significados às coisas que observamos. São essas coisas que dão
o grau de aproximação do nosso
experimento com a realidade. Essa
reflexão é, sem dúvida, uma reflexão filosófica, sobre o sentido do
que observamos, sobre as semelhanças existentes ou não do nosso modelo com a realidade que
pretendemos descrever. Sem estas
reflexões, os experimentos tornamse meras receitas de bolo e os seus
resultados só são aceitos quando
dão exatamente igual às previsões
teóricas. E eis a questão essencial:
um experimento pode aproximarse, mas não dar EXATAMENTE
um resultado teórico, pois na construção da teoria estão contidas simplificações que almejam tornar o
modelo matematizável, mas que
não são EXATAMENTE reproduzidas nas condições experimentais.
Pense nisso. Voltaremos a este assunto em outros contextos da física em outras edições do seu Folhetim. Isso não é algo que estejamos acostumados a pensar. A nossa educação tradicional está repleta
de histórias da Carochinha, de ficções como a do Papai Noel, a da
ABRIL DE 2000
Cegonha e a da exatidão dos experimentos científicos. Caso esteja interessado nesse assunto, leia,
por exemplo, o excelente livro do
Allan Chalmers: “O que é Ciência
Afinal”. Leia, também, o clássico
de Einstein e Leopold Infeld “A
Evolução da Física”. Leia e convide os seus alunos a lerem também. A leitura transforma o mundo, pois transforma as pessoas que
constróem o mundo.
Conclusões
Há um número enorme de formas diferentes de medirmos a aceleração da gravidade. Aqui, tentamos expor apenas três delas (duas
neste número e outra no anterior)
e discutir um pouco do algo que
está subjacente a essas abordagens. Por uma questão de espaço,
deixamos de considerar outros tantos métodos, como, por exemplo,
a muito conhecida utilização de um
pêndulo simples, ou a máquina de
Atwood, ou a menos conhecida
máquina de Morin. Há igualmente
uma série de artefatos mais modernos, utilizando barreiras eletrônicas,
foto-sensores que dão excelentes
resultados. Há artefatos elétricos
um pouco mais simples, como interruptores que são acionados na
queda de um objeto dando partida
em cronômetros a serem travados
pelo impacto mecânico da queda
e não por sensores eletrônicos.
Há, também, alternativas eletronicamente sofisticadas mas bastante acessíveis, como a utilização de
uma câmera de vídeo (handcam)
para filmar a queda de um objeto
junto ao qual tenha sido colocada
uma escala métrica. Dado ao grande número de quadros gerados
pela filmadora (que não é nada mais
que uma máquina de fotografias
múltiplas de alta velocidade) pode-
FOLHE TIM
se observar, quadro a quadro, o
belíssimo resultado do experimento. Pode-se apreciar o surgimento
da progressão aritmética de impares: 1, 3, 5, 7, 9 das distâncias percorridas, denotando a relação
quadrática com o tempo gasto,
como bem descrito no artigo do
Guimarães, já anteriormente mencionado.
Cada uma dessas alternativas
encerra uma concepção própria,
uma forma alternativa de atacar o
problema, traça um conjunto nem
sempre igual de pressupostos, chega a resultados de precisões diferenciadas. Todas elas, no entanto,
da mais simples à mais sofisticada,
carregam a mesma beleza: a tentativa humana de compreender a natureza, de modelar a realidade mais
complexa.
Alexandre Medeiros, PhD
([email protected])
Universidade Federal Rural de
Pernambuco
Francisco Nairon Monteiro Jr., MSc
Universidade Federal Rural de
Pernambuco
Professor, a água é transparente e incolor, não é?
Pois então, por que algumas coisas ficam mais
escuras quando absorvem água e ficam molhadas (por exemplo, a terra e os tecidos)?
13
Onde
está o
Mauro?
PARTE 2
AFINAL
AFINAL,, O QUE A
HOLANDA VAI FAZER
COM O MAURO?
Por que os holandeses estão interessados no transporte de ondas
acústicas? Primeiro porque isso
tem implicações em medições de
tremores de Terra. O segundo motivo, e o mais importante deles, é
que com uma pequena explosão na
superfície da Terra, os Sismólogos
podem escutar o som dessa explosão depois da onda sonora ter interagido com o interior do planeta.
Com base nessas medidas, podese descobrir o que tem lá embaixo. Por exemplo, se tem um puta
poço de petróleo. Como prospecção de petróleo é uma possível
aplicação, a Shell da Holanda botou dinheiro no projeto. Minha função aqui em Delft é fazer a ponte
entre os Físicos e os Sismólogos.
Mauro Santos Ferreira
Se você tem alguma idéia, algo
que deu certo em sala, que motivou os alunos, mande para
nós. Teremos o maior prazer em
divulgar para os outros professores. Você pode enviar a colaboração, de preferência, em arquivo .doc, na fonte Times New
Roman, corpo 12. Endereços:
Virtual: [email protected]
Postal: Rua Macaé, 12
Pé Pequeno - Santa Rosa
Niterói - RJ - Cep: 24240-080
FOLHE TIM
14
PALANQUIM
aluno concordaram em submeter o problema a um juiz imparcial, e eu fui o escolhido. Chegando à sala de meu colega, li
a ques-
à altura do edifício”.
Sem dúvida era uma resposta interessante, e de alguma forma correta, pois satisfazia o
enunciado. Por instantes vacilei quanto ao veredicto. Recompondo-me rapidamente, disse
ao estudante que
tão da
prova,
que dizia:
“Mostrar
como se pode
determinar a altura de um edifício
bem alto com o auxílio de um
barômetro”.
A resposta do estudante foi
a seguinte:
“Leve o barômetro ao alto do
edifício e amarre uma corda
nele; baixe o barômetro até a
calçada e em seguida levante,
medindo o comprimento da corda; este comprimento será igual
ele tinha forte razão para
ter nota máxima, já
que havia
respondido
a questão completa e
corretamente. Entretanto, se ele tirasse nota máxima, estaria caracterizada uma
classificação
para um curso de
Física, mas a resposta não confirmava
isso.
Com a palavra, o professor
Esta história está rolando na internet.
Muitos de vocês já
devem tê-la recebido, mas mesmo
assim, achamos
interessante
publicá-la
neste espaço
do Folhetim.
Seu autor – que
desconhecemos,
uma vez que a história não está assinada – merece
subir no Palanquim, pela oportunidade de reflexão que oferece
para todos nós, professores.
Assim disse Albert Einstein:
“A mente que se abre a uma
nova idéia, nunca voltará a seu
tamanho original.”
Não deixe que a sociedade bitole o seu modo de pensar, seja
sempre criativo.
A HISTÓRIA
DO BARÔMETRO
Algum tempo atrás recebi um
convite de um colega para servir de árbitro na revisão de uma
prova. Tratava-se de avaliar
uma questão de Física, que recebera nota “zero”. O aluno
contestava tal conceito, alegando que merecia nota máxima
pela resposta, a não ser que houvesse uma “conspiração do sistema” contra ele. Professor e
ABRIL DE 2000
ABRIL DE 2000
Sugeri então que fizesse uma
outra tentativa para responder
à questão. Não me surpreendi
quando meu colega concordou,
mas sim quando o estudante resolveu encarar aquele que eu
imaginei lhe seria um bom desafio. Segundo o acordo, ele teria seis minutos para responder
à questão; isto após ter sido prevenido de que sua resposta deveria mostrar, necessariamente,
algum conhecimento de Física.
Passados cinco minutos ele
não havia escrito nada, apenas
olhava pensativamente para o
teto da sala. Perguntei-lhe então se desejava desistir, pois eu
tinha um compromisso logo
em seguida, e não tinha tempo a perder.
Mais surpreso ainda fiquei
quando o estudante anunciou
que não havia desistido. Na
realidade tinha muitas respostas, e estava justamente escolhendo a melhor. Desculpeime pela interrupção e solicitei que continuasse.
No momento seguinte ele
escreveu esta resposta:
“Vá ao alto do edifício, incline-se numa ponta do telhado e solte o barômetro, medindo o tempo de queda desde a largada até o toque com o solo. Depois, empregando a fórmula
h = 1/2gt2 calcule altura do edifício”.
Perguntei então ao meu colega se ele estava satisfeito com
a nova resposta, e se concordava com a minha disposição em
conferir praticamente nota máxima à prova. Concordou, embora sentisse nele uma expressão de descontentamento, talvez
inconformismo.
Ao sair da sala lembrei-me
que o estudante havia dito ter
FOLHE TIM
outras respostas para o problema. Embora já sem tempo, não
resisti à curiosidade e perguntei-lhe quais eram estas respostas.
“Ah!, sim,” – disse ele – “há
muitas maneiras de se achar a
altura de um edifício com a ajuda de um barômetro”.
Perante a minha curiosidade e a já perplexidade de meu
colega, o estudante desfilou as
seguintes explicações.
“Por exemplo, num belo dia
de sol pode-se medir a altura
do barômetro e o comprimento de sua sombra projetada no
solo, bem como a do edifício.
Depois, usando uma simples
regra de três, determina-se a
altura do edifício”.
“Um outro método básico de
medida, aliás bastante simples
e direto, é subir as escadas do
edifício fazendo marcas na parede, espaçadas da altura do barômetro. Contando o número de
marcas tem-se a altura do edifício em unidades barométricas”.
“Um método mais sofisticado
seria amarrar o barômetro na
ponta de uma corda e balançálo como um pêndulo, o que
permite a determinação da
aceleração da gravidade (g).
Repetindo a operação ao nível
da rua e no topo do edifício,
tem-se dois g’s, e a altura do
edifício pode, a princípio, ser
calculada com base nessa diferença”.
“Finalmente”, concluiu, “se
não for cobrada uma solução física para o problema, existem
outras respostas. Por exemplo,
pode-se ir até o edifício e bater
à porta do síndico. Quando ele
aparecer, diz-se:
“Caro Sr. síndico, trago aqui
um ótimo barômetro; se o Sr.
15
me disser a altura deste edifício, eu lhe darei o barômetro
de presente”.
A esta altura, perguntei ao
estudante se ele não sabia
qual era a resposta “esperada”
para o problema. Ele admitiu
que sabia, mas estava tão farto com as tentativas dos professores de controlar o seu raciocínio e a cobrar respostas
prontas com base em informações mecanicamente arroladas, que ele resolveu contestar
aquilo que considerava, principalmente, uma farsa.
Autor desconhecido
Colaboração: Leíse Jogaib
AINDA
ESTÁ
VALENDO!
Lembre-se: o Folhetim propõe-se a colocar em sua página na Internet (com os devidos créditos) os trabalhos
de pesquisa feitos por seus
alunos sobre os temas lançados em números anteriores.
Acrescentamos ainda:
1) Como determinar g usando um pêndulo simples? E a
máquina de Morin?
2) As mais recentes descobertas sobre o Sistema Solar.
16
FOLHE TIM
ABRIL DE 2000
DEU NO JORNAL
Guia ensina a
observar estrelas
*****************************************************************************
Os aficcionados pelo céu já
contam com um guia de endereços
celestes. Lançado semana passada no Planetário, no Rio, o livro
Rumo às estrelas, do jornalista e
editor de Ciências do Museu de
Astronomia (Mast), Alberto
Delerue, traz uma série de diagramas e tabelas que permitem ao leitor identificar as principais constelações do hemisfério austral ou sul
através da simples observação sem
o auxílio de telescópios ou quaisquer outras lentes de aumento.
Voltado para o público leigo, o
livro, editado pela Zahar e que custa R$24, ensina a localizar as estrelas, tendo como base duas unidades de tempo: o mês e a hora.
Segundo o francês Delerue, a cada
três meses, as constelações mudam
de posição, devido ao movimento
de rotação da Terra, transformando a configuração celeste. “É como
se tivéssemos um céu novo para
cada estação do ano”, compara.
O guia também traz tabelas com
as 20 maiores estrelas, as mais brilhantes e as mais próximas do globo terrestre. Depois do Sol, que
dista 150 milhões de quilômetros
da Terra, a estrela que fica mais
perto do planeta azul é a Próxima
de Centauro, situada a 4,3 anosluz da Terra, 270 mil vezes mais
que a distância do Sol. “Foi por isso
que ela recebeu esse nome”, explica Alberto Delerue.
Além de ajudar a identificar estrelas, o guia conta com um glossário astronômico e com tabelas
que indicam a localização de qua-
tro planetas do sistema solar - Vênus,
Marte, Júpiter e Saturno - até o ano
2002. “Atualmente Marte está atra-
FOLHE TIM
Esta é uma publicação mensal da
Galera Hipermídia
Jornalista Responsável:
Sandra Filippo - DRT /BA-739
Redação:
Luiz Alberto Guimarães, Marcelo
Fonte Boa, Sandra Filippo e Ovidio
Brito
Correspondente internacional:
Mauro Santos Ferreira
Desenvolvimento de software e
internet:
Thiago Guimarães e Carlos Eduardo Erbesdobler (Anjinho)
Ilustração:
Marcelo Pamplona
Diagramação:
Ovidio Brito
Apoio Operacional:
Fernando Guimarães
Folhetim é distribuído gratuitamente. A
autoria das colaborações é identificada
em cada artigo e as opiniões emitidas
são de responsabilidade dos seus autores, não refletindo necessariamente a opinião da direção do jornal. Ao remeter
uma colaboração, seu autor concorda
que seja publicada, sem nenhum ônus,
de qualquer espécie, para o Folhetim.
vessando a constelação de Capricórnio, depois de deixar a de Sagitário
em meados de outubro. Já o planeta
Vênus, se encontra, hoje, na constelação de Leão”, diz o autor.
Mas nem só de astronomia fala
Rumo às estrelas. Apesar de basear todo o seu trabalho em precisos cálculos científicos, o autor
acabou arrumando espaço para
a mitologia. Nas 88 páginas do
livro, há um capítulo inteiramente
dedicado a lendas relacionadas
com as constelações, mesclando
ciência e fantasia.
Uma delas é sobre os centauros,
criaturas metade homem, metade
cavalo, com hábitos selvagens, que
viviam ao norte da Grécia. Conta a
mitologia que entre eles havia uma
exceção: Quiron, o mais sábio dos
centauros, com quem se aconselhava Aquiles. Segundo Alberto, Quiron foi atingido por uma flecha, abrindo uma ferida que não cicatrizava.
Não agüentando o sofrimento, o
centauro pede a Zeus, deus dos deuses, que o mate. Desta forma, queria
aliviar a dor, já que, sendo imortal,
sangraria eternamente. Zeus, então,
o tira da Terra e o coloca no céu,
entre as estrelas, originando a constelação que leva seu nome.
Jornal do Brasil, 25/11/99
FOLHETIM
Remetente: Galera Hipermídia
Rua Macaé, 12 - Pé Pequeno
Santa Rosa - Niterói - RJ
Cep: 24240-080