2008 – 2.ª Fase - Areal Editores

© AREAL EDITORES
2008 – 2.ª Fase
10 pontos
5 pontos
5 pontos
54
2008 – 2.ª Fase
5 pontos
© AREAL EDITORES
5 pontos
55
© AREAL EDITORES
2008 – 2.ª Fase
5 pontos
10 pontos
56
2008 – 2.ª Fase
20 pontos
5 pontos
© AREAL EDITORES
10 pontos
57
© AREAL EDITORES
2008 – 2.ª Fase
5 pontos
10 pontos
58
2008 – 2.ª Fase
5 pontos
20 pontos
© AREAL EDITORES
5 pontos
59
© AREAL EDITORES
2008 – 2.ª Fase
5 pontos
5 pontos
10 pontos
60
2008 – 2.ª Fase
5 pontos
5 pontos
© AREAL EDITORES
5 pontos
61
© AREAL EDITORES
2008 – 2.ª Fase
20 pontos
20 pontos
TOTAL
200 pontos
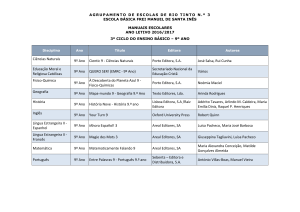
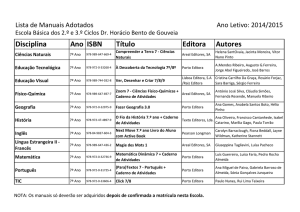
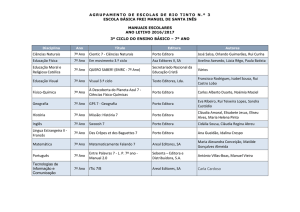
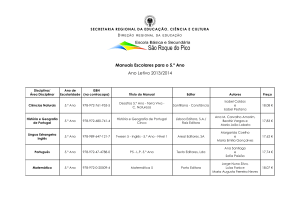
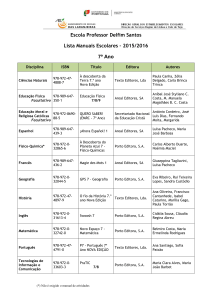
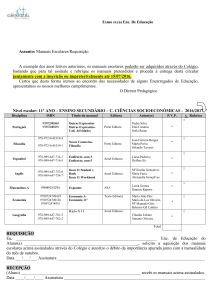
Prova Escrita de Física e Química A, 2008
11.º/12.º Anos de Escolaridade, 2.ª Fase
in www.gave.min-edu.pt
62
2008 – 2.ª Fase
1.
1.1. O som é uma onda mecânica que necessita de um
meio material para a sua propagação. Devido à quase
inexistência de atmosfera na Lua referida no texto,
este e outros fenómenos atmosféricos não existem.
1.2. Efeito de estufa.
1.3. (B). O albedo corresponde à radiação reflectida pelo
planeta. De acordo com o texto, o solo lunar absorve
grande parte da radiação solar, enquanto Vénus, com
uma atmosfera densa, reflecte grande parte dessa radiação.
1.4. (D). Atendendo à expressão da força gravítica
Fg = m * a
Dividindo as expressões para a Terra e Lua
FgT m * aT
=
FgL m * aL
1
Substituindo aL = aT e eliminando m
6
FgT
aT
=
FgL 1
a
6 T
Eliminando aT e isolando FgT, obtém-se
FgT = 6FgL
1.5. (B). Considerando que a aceleração gravítica é seis vezes maior na Terra do que na Lua, a velocidade de
um corpo em queda livre deverá ser seis vezes maior
na Terra do que na Lua. O gráfico B é o único em que
vTerra é maior que vLua.
2.
2.1. (D). As forças representadas correspondem a um par
acção-reacção. As forças que compõem os pares acção-reacção têm de ter módulo igual e sentido contrário, devem ter a mesma direcção e o ponto de
aplicação em corpos distintos. O único diagrama nessas condições é o (D).
2.2. (A) Verdadeira. De acordo com o enunciado, o período é de 2,0 horas a que correspondem 7200 segundos.
(B) Falsa. Um objecto em órbita em torno de um planeta mantém o módulo da velocidade constante, mas
a direcção do vector velocidade varia.
(C) Falsa. O período de 2,0 horas é o tempo necessário para descrever uma órbita completa, cujo perímetro é dado por:
P = 2pr
P = 2p * 1,9 * 106 = 1,19 * 107 m
(D) Verdadeira. A única força que actua sobre o MC é
a força gravítica, cuja direcção é perpendicular ao deslocamento; como tal, o trabalho efectuado pela resultante das forças é nulo.
78
(E) Verdadeira. Como a velocidade angular pode ser
dada por:
2p
w=
T
Então
wT = 2p
O produto do módulo da velocidade angular do MC
pelo período do seu movimento é constante e independente do raio da órbita.
(F) Falsa. Atendendo a que
F»g = F»r
Substituindo as respectivas expressões
M m
v2
G L2 = m
r
r
Eliminando a massa e o raio, obtém-se
M
G L = v2
r
Conclui-se que a velocidade não depende da massa
do satélite.
(G) Verdadeira.
2p
w=
T
2p
w=
7200
w = 8,7 * 10 -4 rad s -1
(H) Falsa. O módulo da velocidade manteve-se constante ao longo da órbita, pelo que a energia cinética
também.
2.3. Cálculo da variação da energia cinética da amostra entre as posições A e B
1
1
DEc = mv2B - mv2A
2
2
Atendendo a que a velocidade final (em B) é nula
1
DEc = 0 - * 0,2 * 0,52
2
DEc = - 0,025 J
Cálculo da variação da energia mecânica do sistema entre as posições A e B
DEm = DEp + DEc
Substituindo
DEm = - 8,16 * 10 -2 - 0,025 = - 0,107 J
Sabendo que
DEm = WF»não conservativas
Como as forças não conservativas correspondem à
força de atrito, tem-se
DEm = |F»atrito| * |d»| * cos q
© AREAL EDITORES
Proposta de resolução
Proposta de resolução
Colocando em ordem a |F»atrito| e substituindo valores
DEm
|F»atrito| =
|d»| * cos q
|F»atrito| =
- 0,107
= 0,21 N
0,51 * cos 180º
Resposta: A intensidade da força de atrito que actuou
sobre a amostra foi de 0,21 N.
|Df|
2.4. 2.4.1. (C). De acordo com a lei de Faraday |e| =
,
Dt
a uma maior variação do fluxo magnético no menor
intervalo de tempo corresponde uma maior força electromotriz induzida. Desta forma, quanto mais rápido é
o movimento, maior é o módulo da força electromotriz induzida; logo, maior é a energia que o circuito
pode disponibilizar.
2.4.2. O outro sinal requerido na modulação denomina-se onda portadora. No processo de modulação,
como o sinal eléctrico do microfone tem uma frequência muito baixa para poder ser emitido directamente,
este é sobreposto a uma onda de elevada frequência,
a onda portadora. Gera-se assim uma onda que resulta da combinação das duas anteriores; esta possui
uma elevada frequência o que a torna propícia para
viajar grandes distâncias e, simultaneamente, guardar
o sinal original.
3.
3.1. 3.1.1. (C). O equilíbrio inicial atinge-se quando as concentrações deixam de sofrer alterações, em t3. A igualdade de concentrações ocorre em t1, quando as linhas
correspondentes às concentrações dos reagentes e
dos produtos se cruzam. Finalmente, a adição de produto ocorre no instante t5, quando a concentração de
HI aumenta repentinamente.
3.1.2. Expressão de equilíbrio
Kc =
3 HI4 2eq
3 H2 4 eq * 3 I2 4 eq
A partir da leitura do gráfico, retiram-se os seguintes dados: [HI]eq = 0,786 mol dm–3; [H2]eq = 0,107 mol dm–3;
[I2]eq = 0,107 mol dm–3. Substituindo na expressão anterior, obtém-se
0,7862
Kc =
0,107 * 0,107
Kc = 53,96
© AREAL EDITORES
Resposta: O valor de Kc, à temperatura referida, é de
53,96.
3.2. 3.2.1. (A) Falsa. Pertencem ao mesmo grupo, mas não
ao mesmo período.
(B) Falsa. Os elementos deste grupo tendem a ter os
valores de energia de ionização mais elevados.
(C) Verdadeira. Como pertencem ao mesmo grupo,
têm uma configuração electrónica no nível de valência
idêntica.
(D) Falsa. O flúor é um dos elementos com menor raio
atómico, ao contrário do iodo, cujo átomo é muito
grande. Esta característica deve-se ao facto de o iodo
ter cinco níveis electrónicos, enquanto o flúor tem
apenas dois níveis electrónicos.
3.2.2. O espectro de emissão do átomo de hidrogénio
é constituído por riscas isoladas sobre um fundo negro
agrupadas em várias séries correspondentes a emissões na região do infravermelho, visível e ultravioleta.
As riscas têm origem nas transições electrónicas de níveis energéticos superiores para níveis energéticos inferiores, num processo denominado desexcitação. A
estas transições está associada a emissão de radiação
electromagnética, que surge como uma risca no espectro. Como os níveis energéticos estão separados
por valores de energia fixos e distintos entre si, as
emissões de radiação surgem igualmente a frequências específicas e espaçadas umas das outras, sendo,
por isso, um espectro descontínuo.
3.2.3. (A). As bases de Brönsted-Lowry são substâncias que aceitam iões H+. As duas únicas substâncias
presentes que podem aceitar iões H+ são a água (H2O)
e o ião fluoreto (F–).
4.
4.1. O balão tem uma capacidade de 250 mL e um erro de
± 0,15 mL. A utilização correcta do balão leva a medições que se situam entre 249,85 mL e 250,15 mL.
(250 mL – 0,15 mL = 249,85 mL e 250 mL + 0,15 mL =
250,15 mL)
4.1.1. (D). A construção do próprio equipamento
prevê a realização da leitura desta forma, minimizando assim o erro de medição.
4.2. Cálculo da quantidade molar de soluto
n=c*v
n = 3,00 * 10 -2 mol dm -3 * 0,250 dm3
n = 7,5 * 10 -3 mol
Cálculo da massa de soluto
m=n*M
m = 7,5 * 10 -3 mol * 248,22 g mol -1
m = 1,8617 g
Resposta: Foi necessário pesar 1,8617 g de tiossulfato
de sódio penta-hidratado de modo a preparar a solução pretendida.
4.3. 4.3.1. (B). Numa operação de diluição como esta,
pode considerar-se que o número de moles obtidos a
partir da solução concentrada é igual ao que se deposita na solução diluída.
nc = nd
79
cc * Vc = Vd * cd
v * cd
Vc = d
cc
Cálculo de ET
(energia libertada pelo corpo C durante a queda)
ET = DEp
g
50,00 * 6,00 * 10
cm3
Vc =
3,00 * 10 -2
4.3.2. (C). A pipeta é um instrumento concebido para
medir pequenos volumes de forma muito exacta.
-3
5.
5.1. (A). De acordo com os dados do enunciado, cada 36 g
de sal necessitam de 100 g de água para se dissolverem. Então para dissolver 90 g são necessárias:
90 * 100
mágua =
36
mágua = 250 g
5.2. Cálculo do número inicial de moles de ácido clorídrico
nHC’ = VHC’ * cHC’
nHC’ = 25 * 10 -3 dm3 * 0,1 mol dm -3
nHC’ = 2,5 * 10 -3 mol
Cálculo da quantidade de ácido clorídrico em
equilíbrio
Atendendo a que a estequiometria é de 1:1
nHC’,eq = nHC’ - nNaOH
nHC’,eq = 2,5 * 10 -3 - 1 * 10 -3
nHC’,eq = 1,5 * 10 -3 mol
Cálculo do pH
pH = - log 3H3O + 4
1
1,5 * 10 -3
35 * 10 -3
2
pH = 1,37
Resposta: O pH da solução resultante é 1,37.
6.
O rendimento corresponde ao quociente entre a energia aproveitada (Eu) para aquecer e a energia disponibilizada (ET) para esse fim.
Cálculo de Eu
(energia absorvida pelo bloco de prata)
Eu = c * m * DT
Eu = 2,34 * 102 * 0,600 * 0,8
Eu = 112,32 J
80
ET = 8 * 10 * 2
ET = 160 J
Cálculo da eficiência
Eu
h=
* 100%
ET
h=
112,32
* 100%
160
h = 70,2%
Resposta: O rendimento do processo é 70,2%.
A solução preparada está saturada, mas não tem depósito.
pH = - log
ET = mgDh
© AREAL EDITORES
Proposta de resolução