Aula 4 - professor Daniel Orquiza de Carvalho

Prof.DanielOrquiza
OndaseLinhas
1
OndaseLinhas
Prof.DanielOrquizadeCarvalho
SJBV
Ondas e Linhas
Linhas de transmissão – SWR, Perda de Retorno e Perda de Inserção
(Páginas 59 a 63 no Livro texto)
•  Tópicos:
§  Coef. de onda estacionária (SWR)
§  Coef. de Reflexão ao longo da linha
§  Perda de Retorno (RL)
§  Perda de Inserção (IL)
EletromagnetismoI
2
Prof.DanielOrquiza
SJBV
Ondas e Linhas
Linhas de transmissão com carga
• 
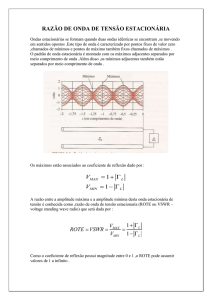
Quando a linha de transmissão é terminada em uma carga, há a formação de
uma onda estacionária ao longo da linha, devido à interferência da onda
incidente com a onda refletida.
• 
Se olharmos para o valor absoluto da tensão ao longo da linha:
V(z) = V0+ 1 + Γ e j(θ - 2β l)
onde θ é a fase do coeficiente de reflexão
Z0 , β
30/03/17
3
IL
V( z ), I( z )
l
+
VL
-
ZL
z
SJBV
Ondas e Linhas
Linhas de transmissão com carga
• 
Quando a linha de transmissão é terminada em uma carga, há a formação de
uma onda estacionária ao longo da linha, devido à interferência da onda incidente com
a onda refletida.
+
+
30/03/17
4
SJBV
Ondas e Linhas
Coef. de Onda Estacionária (SWR)
• 
O valor (absoluto) máximo da onda de tensão formada na L.T. é Vmax.
(
Vmax = V0+ 1 + Γ
• 
O valor mínimo da onda de tensão formada na L.T. é Vmín.
(
Vmin = V0+ 1 - Γ
• 
)
)
A Taxa de Onda Estacionária (SWR – Standing Wave Ratio) é definida como a
razão entre a tensão máxima e a mínima.
Vmax 1 + Γ SWR = = Vmin
1 - Γ 30/03/17
5
SJBV
Ondas e Linhas
Coeficiente de reflexão ao longo da linha
• 
O coeficiente de reflexão foi definido na posição da carga, mas podemos
generalizar esta definição para qualquer posição ao longo da linha.
• 
Se conhecemos o coeficiente de reflexão na carga, e queremos calcular o
coeficiente de reflexão em uma posição qualquer, a uma distância l da carga
usamos:
− − jβ l
0
+ jβ l
0
Ve
Γ(-l) = Ve
= Γ(0) e−2jβ l
Z0 , β
30/03/17
6
IL
V( z ), I( z )
-l
+
VL
-
ZL
z
SJBV
Ondas e Linhas
Potência média ao longo da linha
• 
É possível (Como?) calcular a potência média em qualquer posição ao longo da
linha. Se fizermos isso, descobriremos que a potência é a mesma em qualquer
ponto da linha, e a potência média entregue à carga é:
+
0
2
2
1V
Pavg =
1 - Γ
2 Z0
• 
(
)
O primeiro termo Corresponde à potência incidente, e o segundo à potência
refletida.
IL
V( z ), I( z )
Z0 , β
30/03/17
7
-l
+
VL
-
ZL
z
SJBV
Ondas e Linhas
Perda de Retorno
Um parâmetro importante para caracterizar linhas de transmissão é a Perda de
Retorno, definida como:
RL = -20log Γ [dB]
IL
V( z ), I( z )
Z0 , β
30/03/17
8
-l
+
VL
-
ZL
z
SJBV
Ondas e Linhas
Linhas de transmissão terminada em curto
Se uma linha é terminada em curto, o coeficiente de reflexão é Γ = -1. A tensão
ao longo da linha é a soma da onda incidente e refletida:
V(z) = V0+ (e− jβz − e jβz ) = -2jV0+ sen(βz)
O mesmo acontece para a onda de corrente:
V0+ − jβz jβz
V0+
I(z) = (e +e ) = 2 cos(βz)
Z0
Z0
Assim, a impedância na entrada da linha, a uma distancia l da carga, é:
Z in = jZ 0tan(βl)
30/03/17
IL
V( z ), I( z )
Z0 , β
9
-l
+
VL = 0
-
ZL = 0
z
SJBV
Ondas e Linhas
Linhas de transmissão terminada em curto
Note que tensão e a corrente ao longo da linha formam ONDAS ESTACIONÁRIAS.
Tensão ao longo da linha:
V(z) = -2jV0+sen(β z)
Corrente ao longo da linha:
V0+
I(z) = 2
cos(β z)
Z0
Impedância ao longo da linha:
Z in = jZ 0tan(βl)
10
30/03/17
10
SJBV
Ondas e Linhas
Linhas de transmissão terminada em aberto
• 
Se uma linha é terminada em aberto, o coeficiente de reflexão é Γ = 1. A tensão
ao longo da linha é a soma da onda incidente e refletida:
V(z) = V (e
+
0
• 
− jβz
+e ) = 2V cos(βz)
jβz
+
0
O mesmo acontece para a onda de corrente:
V0+ − jβz jβz
V0+
I(z) = (e − e ) = −2j
sen(βz)
Z0
Z0
• 
Assim, a impedância na entrada da linha, a uma distância l da carga, é:
V( z ), I( z )
Z in = − jZ 0 cot(βl)
Z0 , β
30/03/17
11
l
+
VL
-
Z L = ∞
z
SJBV
Ondas e Linhas
Linhas de transmissão terminada em aberto
Note que tensão e a corrente ao longo da linha formam ONDAS ESTACIONÁRIAS.
Tensão ao longo da linha:
V(z) = 2V0+cos(β z)
Corrente ao longo da linha:
V0+
I(z) = −2j sen(β z)
Z0
Impedância ao longo da linha:
Z in = − jZ 0 cot(βl)
12
30/03/17
12
SJBV
Ondas e Linhas
Linhas de transmissão com l = λ/2
Agora considere uma linha terminada em uma carga ZL arbitrária.
Se o comprimento da linha for múltiplo de λ/2, a impedância da linha carregada
será igual a impedância da carga.
λ
l =n
2
(n= 1,2,3...)
Z in = Z L
IL
V( z ), I( z )
Z L + jZ 0 tan(β l)
Z in = Z 0
Z 0 + jZ L tan(β l)
30/03/17
Z0 , β
13
l
+
VL
-
ZL
z
SJBV
Ondas e Linhas
Linhas de transmissão com l = λ/4
Agora considere uma linha terminada em uma carga ZL arbitrária.
Se o comprimento da linha for múltiplo de λ/4, a impedância da linha carregada
será igual a:
λ
λ
l = + n
4
2
Z 02
Z in =
ZL
(n= 1,2,3...)
IL
V( z ), I( z )
Z L + jZ 0 tan(β l)
Z in = Z 0
Z 0 + jZ L tan(β l)
30/03/17
Z0 , β
14
l
+
VL
-
ZL
z
SJBV
Ondas e Linhas
Linhas com impedância Z0 alimentando linha com impedância Z1
Pergunta: O que acontece se tivermos linhas de transmissão com impedâncias
características distintas em série? Como calculamos o Coeficiente de reflexão Γ?
• 
A carga na primeira linha é a impedância característica da segunda.
Z1 − Z 0
Γ=
Z1 + Z 0
15
30/03/17
15
SJBV
Ondas e Linhas
Linhas com impedância Z0 alimentando linha com impedância Z1
Na interface entre as linhas, parte da onda de tensão é refletida e parte é transmitida
para a segunda linha.
A tensão ao longo da primeira linha é a soma da onda incidente com a refletida.
V(z) = V0+ (e− jβz + Γe jβz )
para z < 0
A tensão ao longo da segunda linha é a fração da onda incidente que é transmitida
na interface.
V(z) = V0+Te− jβz
para z > 0
Onde o Coef. de transmissão (T) é:
2Z1
T=1+ Γ =
Z 0 + Z1
30/03/17
16
SJBV
Ondas e Linhas
Linhas com impedância Z0 alimentando linha com impedância Z1
Um parâmetro importante para caracterizar a interface entre diferentes
componentes e linhas de transmissão de RF é a Perda de Inserção, definida como:
IL = − 20log T
17
30/03/17
[dB]