Exercícios - Paralogike

UNISANTA –Universidade Santa Cecília –Santos SP
Disciplina: Eletrônica I
Próf: João Inácio
Exercícios 1 – Materiais Semicondutores e Junção PN
Aluno:...........................................................Turma:...........N:.................
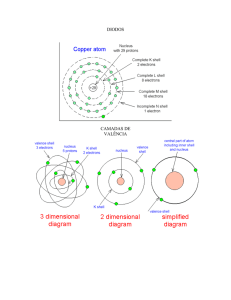
1- Em relação à teoria clássica que trata da estrutura da matéria (átomo- prótons e elétrons)
descreva o que faz um material ser mal ou bom condutor de eletricidade.
2- Qual é a característica de um átomo ionizado?
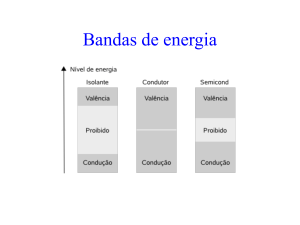
3- Descreva as diferenças entre os materiais considerados: condutores, isolantes e
semicondutores.
4-
O que se entende por rede cristalina ? E por uma ligação covalente ?
5- O que é um material semicondutor puro, ou intrínseco?
6- Por que em um material semicondutor intrínseco somente são criados pares eletronlacunas ?
7- O que são impurezas doadoras? E o que são impurezas aceitadoras?
8- O que é um material semicondutor impuro ou extrínseco?
9- Qual é o portador majoritário em um material tipo P ?
10- O que é um material semicondutor tipo N ?
11- Como é formado um elétron livre em um material semicondutor tipo N ?
12- Como é formada uma lacuna num material semicondutor tipo P ?
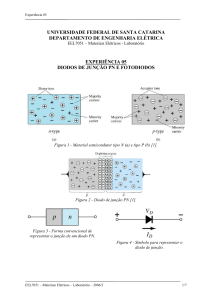
13- O que é uma junção PN ?
14-
Descreva como é formada a região de depleção ou barreira de potencial em uma
junção PN ?
UNISANTA –Universidade Santa Cecília –Santos SP
Disciplina: Eletrônica I
Próf: João Inácio
Exercícios 2 – Materiais Semicondutores e Junção PN
Aluno:...........................................................Turma:...........N:.................
1- Em relação a uma junção PN descreva o que é uma barreira de potencial.
2- Em uma Junção PN onde a região da barreira de potencial é maior, isto é, ocupa maior
área, significa que o material é fortemente dopado ou fracamente dopado? Descreva por
que ?
3- Explique o que ocorre na barreira de potencial quando uma junção PN é reversamente
polarizada.
4- Explique o que ocorre na barreira de potencial quando uma junção PN é diretamente
polarizada.
5-
Faça o desenho da junção PN diretamente e inversamente polarizada utilizando uma
fonte de tensão DC.
N
P
N
P
+
-
+
-
Vcc
Vcc
6- Descreva o que é um diodo semicondutor de junção.
7- Qual material da junção PN é o ligado o terminal do diodo nomeado de Cátodo ?
8- Faça o desenho do símbolo do diodo e escreva as setas de tensão e corrente quando o
mesmo está polarizado diretamente e polarizado reversamente.
2
UNISANTA –Universidade Santa Cecília –Santos SP
Disciplina: Eletrônica I
Próf: João Inácio
Exercícios 3 – O diodo semicondutor de junção
Aluno:...........................................................Turma:...........N:.................
1- Dada a equação do diodo:
V
nVT
Id = Is ( e - 1 )
onde:
Id é a corrente direta do diodo em Ampéres
Is é a corrente de saturação em Ampéres
V é a tensão aplicada nos terminais do diodo em Volts
n é o ajuste de adequação da curva (1< n ≤ 2)
VT é a tensão térmica ou termodinâmica do diodo calculada por:
VT =
KT
q
Sendo: K = Constante de Boltzmann = 1,38 . 10-23 j/K
T = Temperatura em Kelvin T = (273 + T 0C)K
q = Carga do elétron q = 1,602 . 10-19C
Calcule a tensão térmica VT e a corrente direta Id de um diodo de junção semicondutor de
silício com os seguintes valores:
Is = 1,2 pA
V= 0,4V
Temperatura ambiente de T0C = 250C
Considere n =1
2- Considere um diodo de silício em uma temperatura ambiente de T0C = 250C com a
tensão V aplicada nos seus terminais conforme mostra a tabela abaixo. Com n=1, calcule
para cada valor de tensão da tabela a corrente direta Id correspondente e construa um
gráfico Id x V das características direta do diodo. Obs:Is = 1,0 pA
V (volts)
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
Id (mA)
3
UNISANTA –Universidade Santa Cecília –Santos SP
Disciplina: Eletrônica I
Próf: João Inácio
Exercícios 4 – Aplicações do diodo semicondutor de junção
Aluno:...........................................................Turma:...........N:.................
1- Dado o circuito mostrado na figura abaixo:
a) Calcule a tensão média contínua Vdc na carga RL.
b) A tensão de pico retificada Vpr.
c) A corrente direta Id no diodo D1
d) A tensão Reversa máxima VRm nos terminais do diodo.
e) Esboce a forma de onda da tensão (VRL) na carga RL.
D1
Vent
60Hz
RL
4,7KΩ
15Vca
60Hz
2- Dado o circuito do retificador de ½ onda com Capacitor de Filtro mostrado na figura
abaixo:
a) Calcule a tensão média contínua Vdc na carga RL.
b) A tensão de pico retificada Vpr
c) A tensão de pico à pico da Ondulação Vpp.
d) Corrente direta Id no diodo D1
Vrms da ondulação
e) Sabendo que δ = Fator de ripple, onde: δ =
Vdc Tensão média contínua
determine o valor de δ.
D1
Vent
60Hz
45Vca
60Hz
C
RL
23KΩ
100uF
4
UNISANTA –Universidade Santa Cecília –Santos SP
Disciplina: Eletrônica I
Próf: João Inácio
Exercícios 5 – Aplicações do diodo semicondutor de junção
Aluno:...........................................................Turma:............N:..................
1- Dado o circuito mostrado na figura abaixo:
a) Calcule a Tensão média contínua Vdc na carga RL.
b) A tensão de pico retificada Vpr.
c) A corrente direta Id nos diodos.
d) A tensão Reversa máxima Vrm nos terminais dos diodos.
e) Esboce a forma de onda da tensão (VRL) na carga RL.
D1
Vent
60Hz
D2
16V
60Hz
D3
RL
23KΩ
D4
2- Dado o circuito do retificador de ½ onda com Capacitor de Filtro mostrado na figura
abaixo:
a) Calcule a tensão média contínua Vdc na carga RL.
b) A tensão de pico retificada Vpr
c) A tensão de pico à pico da Ondulação Vpp.
d) Corrente direta Id nos diodos.
Vrms da ondulação
e) Sabendo que δ = Fator de ripple, onde: δ =
Vdc
Tensão média contínua
determine o valor de δ.
D1
Vent
60Hz
D2
24V
60Hz
D3
D4
C
100 uF
RL
12 KΩ
5
UNISANTA –Universidade Santa Cecília –Santos SP
Disciplina: Eletrônica I
Próf: João Inácio
Exercícios 5 – Capacitor em regime DC
Aluno:...........................................................Turma:............N:..................
1- No circuito abaixo, a chave K é fechada
rapidamente alimentando o circuito com 18 Volts
conforme é mostrado na figura abaixo:
a) Calcule o valor da intensidade máxima da
corrente Imax no instante do fechamento.
b) A equação da corrente em função do tempo.
c) A intensidade da corrente no instante t= 0,10s
a partir do fechamento da chave K.
d) A constante de tempo do circuito RC.
e) A carga do capacitor no instante t= 0,16 s a
partir do fechamento da chave K.
f) A tensão nos terminais do capacitor no
instante t= 0,16 s a partir do fechamento da
chave K.
K
RL
2,3KΩ
E
18V
C
38 uF
2- No circuito da figura abaixo a chave S seleciona as ligações entre o ponto 3 e ponto 1
fechando K1 ou seleciona a ligação entre o ponto 3 e 2 fechando K2 :
1,4 KΩ
S
K1
3
K2
C
1500 uF
E
24V
1KΩ
a) Determine a constante de tempo do circuito RC.
b) Calcule o valor da tensão nos terminais do capacitor no instante 2s após o
fechamento da chave K1.
c) Considere que a chave K1 foi fechada durante um tempo equivalente 5 vezes a
constante de tempo, ficando o capacitor completamente carregado, e logo após foi
fechada a chave K2. Calcule o valor da tensão nos terminais do capacitor no instante
decorrido de 2 segundos após o fechamento da chave K2.
d) Na condição exposta no item anterior, calcule o valor da tensão nos terminais do
capacitor no instante decorrido de 4 segundos após o fechamento da chave K2.
6