Relatorio de Daniel

UNIVERSIDADE FEDERAL DE PERNAMBUCO
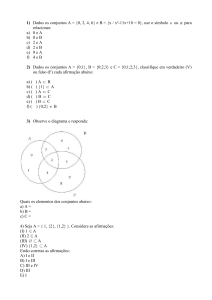
DEPARTAMENTO DE ESTATÍSTICA
Medida e Probabilidade
Aluno: Daniel Cassimiro Carneiro da Cunha
Professor: Andre Toom
1
Resumo
Este trabalho contem um resumo dos principais resultados de Medida e
Integração necessários para o curso de Medida e Probabilidade. O conceito
de medida é apresentado e algumas de suas propriedades são discutidas.
Em seguida, é introduzido o conceito de integral de Lebesgue e alguns
teoremas importantes são provados.
2
Conteúdo
1
2
Medida
1.1 Conjuntos Nulos . . . . . . . . . .
1.2 Medida Exterior . . . . . . . . . .
1.3 Conjuntos mensuraveis Lebesgue e
1.4 Propriedades básicas da medida de
1.5 Conjuntos de Borel . . . . . . . .
.
.
.
.
.
4
4
5
7
8
9
Funções Mensuraveis
2.1 A reta estendida . . . . . . . . . . . . . . . . . . . . . . .
2.2 Funções mensuráveis . . . . . . . . . . . . . . . . . . . .
2.3 Propriedades . . . . . . . . . . . . . . . . . . . . . . . . .
11
11
11
12
3
. . . . . . . . . . . .
. . . . . . . . . . . .
medida de Lebesgue .
Lebesgue . . . . . .
. . . . . . . . . . . .
Capítulo 1
Medida
1.1
Conjuntos Nulos
Definição 1.1.1. Seja I ⊂ R um intervalo limitado, ou seja I = [a, b],
I = [a, b), I = (a, b] ou I = (a, b). Definimos o comprimento de I como
sendo l(I) = b − a.
Temos para um caso particular que l(∅) = l(a, a) = a − a = 0. Da
mesma forma, l({a}) = l([a, a]) = a − a = 0, ou seja, conjuntos com
apenas um elemento tem comprimento 0. A definição a seguir permite
estender a ideia de conjuntos que possuem ’comprimento zero’ a conjuntos
mais gerais.
Definição 1.1.2. Dizemos que A ⊆ R é um conjunto nulo se para todo
ε > 0 podemos encontrar uma sequencia de intervalos {In : n > 1} tal que
A⊆
∞
[
In
∞
X
e
n=1
l(In ) < ε
n=1
Diremos que os (In )n>1 cobrem o conjunto A. Note que pela definição
1.1.2, o conjunto vazio e o conjunto unitário são conjuntos nulos. Ainda,
4
se A é um conjunto finito, então A é um conjunto nulo. Para mostrar isso
faremos uso da proposição 1.1.1 abaixo que é uma ferramenta útil para
provar se um conjunto é nulo.
Proposição 1.1.1. Seja (An )n>1 uma sequencia de conjuntos nulos. Então
a união destes conjuntos,
A=
∞
[
An
n=1
é um conjunto nulo.
Usando o resultado acima, mostra-se facilmente que um conjunto finito
é um conjunto nulo. O mesmo resultado se aplica a conjuntos contaveis.
Temos, por exemplo, que o conjunto Q dos números racionais , e o conjunto
Z dos números inteiros são conjuntos nulos.
1.2
Medida Exterior
Vamos agora estender a noção de comprimento para uma noção mais geral,
que é a de medida exterior.
Definição 1.2.1. A medida exterior (de Lebesque) de um conjunto A ⊆ R
é dada por
m? (A) = inf IA ,
5
em que
IA =
∞
X
l(In ) : In são intervalos, A ⊆
n=1
∞
[
In
.
n=1
No caso de IA = ∅, faremos a seguinte convenção de que m? (A) = ∞.
Desta forma, como o conjunto IA é limitado inferiormente por 0, o infimo
sempre existe.
O resultado a seguir apresenta algumas propriedades de m? (A).
Teorema 1.2.1. Sejam A ⊆ R e B ⊆ R e t ∈ R. Então valem as seguintes
propriedades
(i) (Não-Negatividade) m? (A) > 0.
(ii) (Monotonicidade) Se A ⊂ B então m? (A) 6 m? (B).
(iii) (Sub-aditividade contavel) Para toda sequencia de conjuntos (An )n>1 ,
!
∞
∞
X
[
?
m? (An ).
m
An 6
n=1
n=1
(iv) (Invariancia a translação) m? (A) = m? (A + t).
Concluímos a seção mostrando dois resultados importantes. O primeiro
diz que a nossa definição de medida exterior é consistente com o conceito
de medida nula visto na seção anterior.
Teorema 1.2.2. O conjunto A ⊆ R é um conjunto nulo se e somente se
m? (A) = 0.
6
1.3
Conjuntos mensuraveis Lebesgue e medida de Lebesgue
Definição 1.3.1. Um conjunto E ⊆ R é dito ser mensurável (a Lebesgue)
se para todo conjunto A ⊆ R
m? (A) = m? (A ∩ E) + m? (A ∩ Ec ).
Neste caso, escrevemos E ∈ M.
De A = (A ∩ E) ∪ (A ∩ Ec ) segue que
m? (A) 6 m? (A ∩ E) + m? (A ∩ Ec ).
Daí, para mostrar que E ∈ M, basta verificar a desigualdade
m? (A) > m? (A ∩ E) + m? (A ∩ Ec ).
Como exemplos de conjuntos mensuráveis citamos os intervalos e os conjuntos nulos. Vamos agora apresentar algumas propriedades de M.
Proposição 1.3.1. Temos que
(i) R ∈ M,
(ii) Se E ∈ M então Ec ∈ M,
(iii) Se En ∈ M para n = 1, 2, . . . então
S∞
n=1 En
∈ M.
Ainda, se En ∈ M, n = 1, 2, . . ., e Ei ∩ Ej = ∅ para i 6= j, então
!
∞
∞
[
X
?
En =
m? (En ).
m
n=1
n=1
7
(1.1)
As condições (i)-(iii) implicam que M é uma σ-álgebra. Uma função
que toma valores em [0, ∞] definida em uma σ-álgebra é chamada medida,
ou seja, se for contavelmente aditiva.
Definição 1.3.2. Escrevemos m(E) ao invés de m? para qualquer E em M
e chamar m(E) de medida de Lebesgue do conjunto E.
1.4
Propriedades básicas da medida de Lebesgue
Já que a médida de Lebesgue é nada mais que a medida exterior restrita a
uma classe especial de conjuntos, algumas propriedades da medida exterior
são automaticamente herdadas pela medida de Lebesgue, como mostra a
proposição a seguir:
Proposição 1.4.1. Suponha que A, B ∈ M.
(i) Se A ⊂ B então m(A) 6 m(B).
(ii) SeA ⊂ B e m(A) é finito então m(B − A) = m(B) − m(A).
(iii) m é invariante a translação.
O resultado a seguir mostra que uma sequencia monotona de conjuntos
mensurais se comporta de maneira esperada com respeito a m.
Teorema 1.4.1. Suponha que An ∈ M, para todo n > 1. Então temos
que
8
(i) Se An ⊂ An+1 para todo n, então
!
[
An = lim m(An ),
m
n→∞
n
(ii) Se An ⊃ An+1 para todo n e m(A1 ) < ∞, então
!
\
m
An = lim m(An ).
n→∞
n
(1.2)
Como consequencia do teorema temos os seguintes resultados
Teorema 1.4.2. A função m satisfaz:
(i) m é finitamente aditiva, ou seja, para pares de conjuntos disjuntos
(Ai ) temos que
m
n
[
!
Ai
=
n
X
m(Ai )
i=1
i=1
para todo n;
(ii) m é continua no vazio, ou seja, Se (Bn ) decresce para ∅, então m(Bn )
decresce para 0.
1.5
Conjuntos de Borel
A definição de M não permite que verifiquemos facilmente se um particular
conjunto pertence a M. Portanto, é útil introduzir uma nova estrutura que
permita trabalhar com conjuntos abertos. O resultado a seguir permite
construir novas σ-álgebras.
9
Teorema 1.5.1. A intersecção de uma família de σ-álgebras é uma σálgebra.
Definição 1.5.1. Ponha
B=
\
{F : F é uma σ-álgebra contendo todos os intervalos}
Dizemos que B é uma σ-álgebra gerada por todos os intervalos e que os
elementos de B são conjuntos de Borel.
Teorema 1.5.2. Se ao invés de intervalos considerarmos intervalos abertos,
então o conjunto B ainda é o mesmo.
10
Capítulo 2
Funções Mensuraveis
2.1
A reta estendida
O comprimento de R é ilimitado superiormente, ou seja, infinito. Para lidar com isto nós definos a medida de Lebesgue para conjuntos de medidas
finitas e infinitas. Para tratar funções de conjuntos adequadamente, é conviniente permitir que as funções tomem valores infinitos. Assim, definimos
a reta extendida como sendo R̄ = R ∪ {−∞, +∞}. Definimos ∞ · ∞ = ∞,
a × ∞ = ∞ se a > 0, a × ∞ = −∞ se a < 0, a + ∞ = ∞, para todo a e
∞ × 0 = 0.
2.2
Funções mensuráveis
O domínio das funções que iremos considerar será usualmente R. Agora
temos a liberdade de definir f exceto por um conjunto nulo. Uma vez
mostrado que f e g são iguais em R − E onde E é um conjunto nulo, então
f = g para todos os propositos praticos. Para formalizar isso dizemos que
f = g q.t.p.
11
Definição 2.2.1. Suponha que E é um conjunto mensurável. Dizemos que
a função f : E → R é mensurável Lebesgue se para todo intervalo I ⊂ R
f−1 (I) = {x ∈ R : f(x) ∈ I} ∈ M
O teorema a seguir dá algumas definições equivalentes de funções mensuráveis.
Teorema 2.2.1. As seguintes condições são equivalentes :
(i) f é mensurável.
(ii) Para todo a, f−1 ((a, ∞)) é mensurável.
(iii) Para todo a, f−1 ([a, ∞)) é mensurável.
(iv) Para todo a, f−1 (−∞, a)) é mensurável.
(v) Para todo a,f−1 (−∞, a]) é mensurável.
2.3
Propriedades
A classe de funções mensuráveis é bastante rica, como mostra o
Teorema 2.3.1. O conjunto das funções mensuráveis é um espaço vetorial
e é fechado sobre a multiplicação.
Teorema 2.3.2. Suponhas que F : R×R → R é uma função continua e que
f e g são funções mensuráveis. Então h(x) = F(f(x), g(x)) é mensurável.
12
Vamos definir
f+ (x) =
e
f− (x) =
se f(x) > 0
se f(x) 6 0
f(x)
0
0
−f(x)
se f(x) > 0
se f(x) 6 0
Então temos o seguinte resultado
Teorema 2.3.3.
(i) f é mensurável se e somente se f+ e f− são mensuráveis.
(ii) Se f é mensurável então |f| é mensurável. A reciproca é falsa.
Temos ainda que
Teorema 2.3.4. Sejam {fn } uma sequencia de funções mensuráveis definidas em E e que tomam valores reais. Então são mensuráveis as seguintes
funções:
max fn ,
n6k
min fn ,
n6k
sup fn ,
n∈N
, inf fn ,
n∈N
lim sup fn ,
n→∞
lim inf fn .
n→∞
As coisas ficam um pouco mais complicadas quando consideramos conjuntos nulos. Entretanto, quando mudamos uma função apenas num conjunto nulo, não alteramos a sua propriedade de mensurabilidade.
Teorema 2.3.5. Se f é mensuravel, g é arbitraria e {x : f(x) = g(x)} é nulo,
então g é mensurável.
13
Seja uma sequencia de funções mensuraveis fn tal que fn → f q.t.p.
Então f é mensurável.
14