Lista nº 8

Aprimorando os Conhecimentos de Mecânica
L ista 8
Grandezas Cinemáticas II
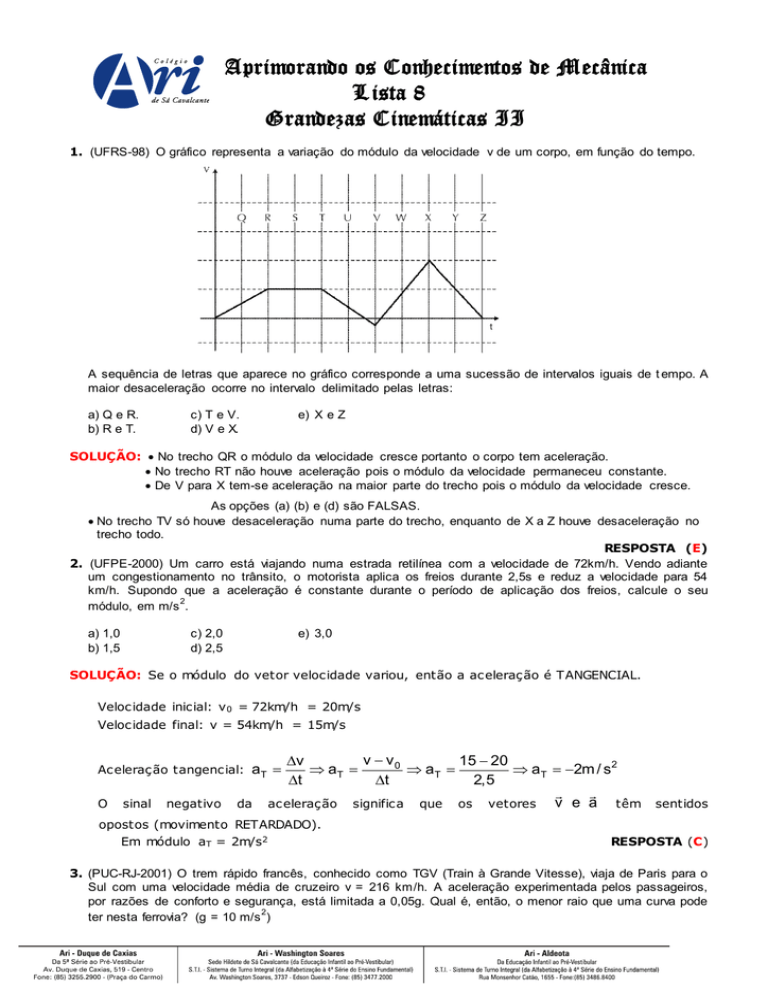
1. (UFRS-98) O gráfico representa a variação do módulo da velocidade v de um corpo, em função do tempo.
A sequência de letras que aparece no gráfico corresponde a uma sucessão de intervalos iguais de t empo. A
maior desaceleração ocorre no intervalo delimitado pelas letras:
a) Q e R.
b) R e T.
c) T e V.
d) V e X.
e) X e Z
SOLUÇÃO:  No trecho QR o módulo da velocidade cresce portanto o corpo tem aceleração.
 No trecho RT não houve aceleração pois o módulo da velocidade permaneceu constante.
 De V para X tem-se aceleração na maior parte do trecho pois o módulo da velocidade cresce.
As opções (a) (b) e (d) são FALSAS.
 No trecho TV só houve desaceleração numa parte do trecho, enquanto de X a Z houve desaceleração no
trecho todo.
RESPOSTA (E)
2. (UFPE-2000) Um carro está viajando numa estrada retilínea com a velocidade de 72km/h. Vendo adiante
um congestionamento no trânsito, o motorista aplica os freios durante 2,5s e reduz a velocidade para 54
km/h. Supondo que a aceleração é constante durante o período de aplicação dos freios, calcule o seu
2
módulo, em m/s .
a) 1,0
b) 1,5
c) 2,0
d) 2,5
e) 3,0
SOLUÇÃO: Se o módulo do vetor velocidade variou, então a aceleração é TANGENCIAL.
Velocidade inicial: v 0 = 72km/h = 20m/s
Velocidade final: v = 54km/h = 15m/s
Aceleração tangencial:
O
sinal
negativo
aT 
da
v  v0
v
15  20
 aT 
 aT 
 aT  2m / s2
t
t
2,5
aceleração
opostos (movimento RETARDADO).
Em módulo aT = 2m/s2
significa
que
os
vetores
v e a
têm
sentidos
RESPOSTA (C)
3. (PUC-RJ-2001) O trem rápido francês, conhecido como TGV (Train à Grande Vitesse), viaja de Paris para o
Sul com uma velocidade média de cruzeiro v = 216 km/h. A aceleração experimentada pelos passageiros,
por razões de conforto e segurança, está limitada a 0,05g. Qual é, então, o menor raio que uma curva pode
2
ter nesta ferrovia? (g = 10 m/s )
a) 7,2 km
b) 93 km
c) 72 km
d) 9,3 km
e) não existe raio mínimo
SOLUÇÃO: Numa curva a aceleração experimentada, por um passageiro, é a componente centrípeta.
aC 
R
v2
v 2 v  216km / h  60m / s
R 

2
R
aC aC  0,05g  0,5m / s
(60)2
 R  7200m  R  7,2km
0,5
RESPOSTA (A)
4. (UFPB-98) Um corpo desloca-se numa trajetória retilínea. Às 10 horas e 30 minutos, sua velocidade é de
40km/h num determinado sentido e, às 10 horas e 45 minutos, é de 60km/h no sentido oposto ao anterior.
2
O módulo da aceleração média do corpo neste intervalo de tempo, em km/h , é:
a) 20
b) 80
c) 100
d) 240
e) 400
SOLUÇÃO: As velocidades nos instantes t 1 = 10h e 30min e t 2 = 10h e 45min estão representadas na figura.

a
t
1

v
1
am 
a
t
2


v

v
2
s
(
t
)
v  v 2  v1  60  40  100km / h
v 

t  15min  1 h
t 
4

100
 a  400km / h2
1
4
RESPOSTA (E)
Em módulos a = 400km/h2
NB: O sinal negativo da aceleração significa que o vetor
Na figura o vetor
a tem sentido contrário ao da orientação da trajetória.
a está apontando para a esquerda.
5. (UECE-98) Um ventilador acaba de ser desligado e está parando vagarosamente, girando no sentido
horário, conforme a figura abaixo. O vetor aceleração da pá do ventilador no ponto P é melhor representado
na opção:
a)
b)
c)
d)
SOLUÇÃO: O ventilador está girando no sentido horário mas parando vagarosamente. No ponto P os vetores
atuantes são:
v : vetor velocidade (tangente à trajetória)
a T : aceleração tangencial no sentido contrário

a
ao da velocidade (movimento

aT
retardado)

aC : aceleração centrípeta na direção do raio e apontando para o centro da
ac

curva (trajetória curva)

a : aceleração
v
RESPOSTA (D)
resultante no ponto P.
6. (UFC) Um automóvel entra numa curva de 200 m de raio, de uma estrada cujas condições permitem uma
2
aceleração centrípeta máxima de apenas 2 m/s sem que aconteça derrapamento. Determine a maior
velocidade, em km/h, com que o automóvel pode ser conduzido na curva, sem derrapamento.
a) 72
b) 60
c) 36
d) 20
e) 18
SOLUÇÃO: Numa curva, quanto maior a velocidade maior será a aceleração centrípeta.
v2
aC 
 v 2  aC .R
R
Se a aceleração centrípeta máxima é aC = 2m/s 2, então para a velocidade máxima tem-se:
v2 = 2 x 200  v = 20 m/s  v = 20 x 3,6 
v  72km/h
RESPOSTA (A)
7. (ENEM 2009) O Brasil pode se transformar no primeiro país das Américas a entrar no seleto grupo das
nações que dispõem de trens-bala. O Ministério dos Transportes prevê o lançamento do edital de licitação
internacional para a construção da ferrovia de alta velocidade Rio-São Paulo. A viagem ligará os 403
quilômetros entre a Central do Brasil, no Rio, e a Estação da Luz, no centro da capital paulista, em uma hora e
25 minutos.
Disponível em: http://oglobo.globo.com. Acesso em: 14 jul. 2009.
Devido à alta velocidade, um dos problemas a ser enfrentado na escolha do trajeto que será percorrido pelo
trem é o dimensionamento das curvas. Considerando-se que uma aceleração lateral confortável para os
passageiros e segura para o trem seja de 0,1 g, em que g é a aceleração da gravidade (considerada igual a 10
2
m/s ), e que a velocidade do trem se mantenha constante em todo o percurso, seria correto prever que as
curvas existentes no trajeto deveriam ter raio de curvatura mínimo de, aproximadamente,
a) 80 m.
b) 430 m.
c) 800 m.
d) 1.600 m.
e) 6.400 m.
SOLUÇÃO:
Quando se tem pela frente uma questão em que se deve chegar a um valor numérico, é recomendável dar
uma “olhadinha” nos valores que estão nas opções. Se a diferença entre eles é relativamente grande, pode -se
usar e abusar dos arredondamentos, como será feito nesse problema.
t = 85 min = 5,1 103 s
S 4  105

 80 m/s.
A velocidade média (vm) do trem-bala é: vm 
t 5  103
Dados:
S = 403 km
400 km = 4 105 m;
A aceleração lateral (centrípeta - ac ) é: ac 
5 103 s.
v2
v2
802
r 

 r  6.400 m.
r
ac 0,1(10)
RESPOSTA (E)
8. (PUC-PR-MODIFICA DA) Um automóvel trafega em uma estrada retilínea. No instante t = 0 os freios são
acionados, causando uma aceleração constante até anular a velocidade, como mostra a figura.
A tabela mostra a velocidade em determinados instantes.
Com base nestas informações, assinale a afirmativa correta a respeito do movimento:
A) O automóvel apresenta uma aceleração no sentido do deslocamento.
B) A aceleração do veículo é –1,5 m/s 2.
C) A velocidade varia de modo inversamente proporcional ao tempo decorrido.
D) A velocidade do veículo se anula no instante 7,5s.
SOLUÇÃO:
A) (F) O movimento é uniformemente retardado, logo a velocidade e a aceleração têm sentidos
opostos. Desta maneira, a aceleração tem sentido contrário ao desloca mento.
B) (F)
C) (F) Duas grandezas são inversamente proporcionais quando o produto delas é constante. No caso
desta tabela, V e T variam linearmente, pois para intervalos de tempos iguais tem-se variações iguais
de velocidade.
D) (V)
----> t = 7,5 s
RESPOSTA (D)
9. (UFC – MODIFICADA) Uma criança num carrossel descreve trajetória circular, de raio r = 1,0m, com
velocidade variável. A figura mostra a criança em um dado instante de tempo em que sua aceleração tem
módulo a = 32m/s 2, e aponta na direção e sentido indicados.
Nesse instante, o módulo da velocidade da criança é:
a) 2,0m/s
b) 4,0m/s
c) 6,0m/s
d) 8,0m/s
e) 10,0m/
SOLUÇÃO:
RESPOSTA (B)
10. Um engenheiro automotivo projeta um carro ecologicamente correto e eficiente que polui pouco e
desenvolve altas velocidades.
O carro é projetado de maneira que, quando acelerado maximamente em linha reta, a sua velocidade aumenta
10km/h a cada segundo. Partindo de uma velocidade inicial de 20km/h, ao final de 8s de aceleração máxima, o
carro terá atingido a velocidade de:
a) 120km/h
b) 100km/h
c) 80km/h
d) 60km/h
e) 40km/h
SOLUÇÃO: Observe que a aceleração tangencial do carro é: a = 10km/h/s
----->
RESPOSTA (B)
GABARITO
01. E
02. C
03. A
04. E
05. D
06. A
07. E
08. D
09. B
10. B